在情境中探索 在模型中抽象

黄银银

摘 要：在教学“数的初步认识”时，教师应从学生的生活经验和已有知识出发，为学生创造一个具有探究性的学习环境，借助一些具体实物模型将抽象的数转化为直观图形，让学生在经历“具体—抽象—具体”的认知过程中，达到理解数的意义，建立数的概念的目标，有效发展学生自主学习能力，落实数学核心素养.

关键词：实物模型；数的意义；数的概念

“数的认识”是小学阶段的重点学习内容，是数学最基础的知识之一，是学好数学的基础.而对于“数的初步认识”可谓是数学教学的重中之重，其在帮助学生建立数感，培养学生符号意识等方面发挥着重要的作用，是学生进一步学习的必要知识基础.因此，在教学整数、分数、小数的初步认识时，教师应从学生已有知识和经验出发，巧借一些具体实物模型让学生更好地理解数的意义，建立数的概念^［1］.

1 巧借“卡纸”建立整数概念

认识数先从认识1～5各数开始，它是后续学习10以内的数及10以内的加减法的基础，当然它也是后续学习两位数、多位数及进行两位数加减法和多位数加减法的前提，其在数的认识系列教学中具有重要的意义.很多教师在教学“1～5各数的认识”时，认为这些知识学生在幼儿园或者没有上幼儿园的时候就已经知道了，所以没有必要深挖，只要学生会读、能写就可以了.确实，这些内容学生在入学前就已经掌握了，但是学生对这些数的认识仅是机械的记忆或表象的认识，学生并不理解各数的意义.因此，在教学中，教师有必要引导学生结合生活经验进一步认识各数，在会读、能写的基础上，让学生理解各数的意义，建立整数概念.

案例1：认识数字“1”

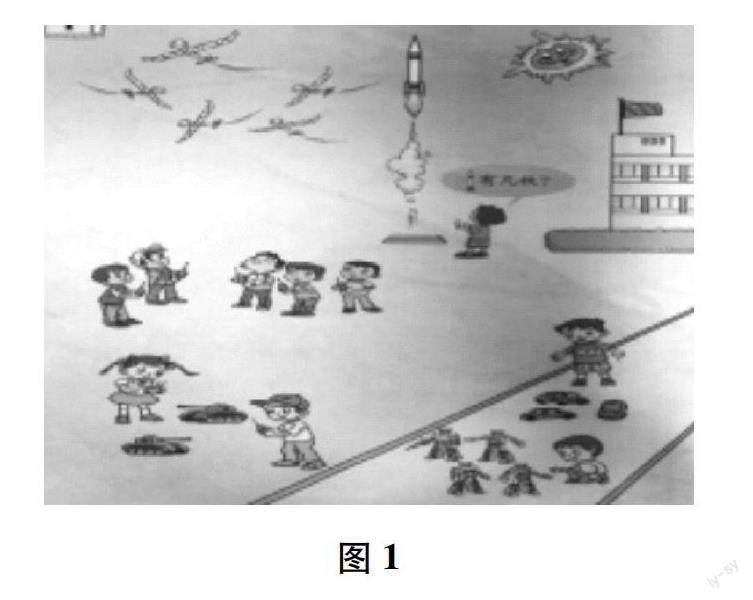
师：认真观察图1，说一说，图中有几枚火箭？

生齐声答：1枚.

师：很好，你还能在图1中找到个数是1的物品吗？

生1：1个太阳.

生2：1面红旗.

……

师：大家真棒.现在我们用一个圆形卡纸来表示它们的个数.比如说，1个太阳我们就用一个圆形卡纸来表示.现在这个卡纸表示什么呢？

生齐声答：1个太阳.

师：非常好！其实数字1可以表示很多东西，你现在想用它表示什么呢？（学生积极思考，踊跃发言）

生3：表示1枚火箭.

生4：表示1块糖.

……

设计意图：教学中，教师先是借助具体问题让学生通过观察寻找图中的数字1，以此培养学生的数感.在此基础上，教师借助圆形卡纸这一实物图形引导学生经历“具体—抽象—具体”的过程，让学生理解了数字1的意义.在此基础上，学生理解2～5各数的意义自然也就水到渠成了，促进了整数概念的建构.

2 巧借“学具纸”建立分数概念

在生活中有许多需要平均分的问题，这些问题是难以利用整数来处理的，为了让数学更好地服务生活，有必要对数进行扩充，为此产生了分数.分数的读法、写法、计算方法、意义等与整数有着较大的差异，为此很多学生在理解分数时容易出现畏难情绪，尤其在应用分数解决现实问题时，更是因为无法理解整体“1”而产生错误.分数因生活需要而产生，因此在教学中不妨将其融于生活，以此淡化数学知识的抽象感，让学生结合生活经验更好地理解分数、应用分数，理解部分与整体的关系，建立一种“关系认识”的思维方式，以此理解分數的意义，建立分数概念^［2］.

案例2：认识“?”

师：中秋节大家要吃什么呢？

生齐声答：月饼.

师：真棒！月饼寓意着团圆，所以这一天大家会坐在一起分吃月饼.不过提到分吃，问题就来了，如果将一个月饼平均分给两个人，那么每人能够分到多少呢？

生1：每人半块.

师：在生活中我们确实这样说，那么数学中到底如何表示“半块”呢？今天我们一起来探个究竟.

师：如果我们将“一块月饼”用数字1表示，你认为“半块月饼”用哪个数字表示比较合适呢？（学生积极互动交流，得到了很多数字）

师：大家非常有创造力，虽然表示方法不同，但是思考的方向是一致的.在数学上统一用?来表示.（给出正确答案的学生露出了开心的笑容，其他学生也频频点头，感觉这样表示最合适）

教师给出分数的读法、写法后，与学生继续探究分数的意义.

师：思考一下，?表示什么？

生2：表示把1块月饼分成2份，其中的1份是它的?.

师：那还有一份会是多少呢？

生齐声答：也是它的?.

师：也就是说每份都是它的?.

师：刚刚我们是将一块月饼分成了?，那么你能通过“折一折”“涂一涂”等活动，在这些大小不同，形状不同的学具纸中找到?吗？

问题给出后，学生积极动手操作，很快就在不同形状、不同大小的学具纸上找到了?.

师：它们明明大小、形状都不同，为什么我们能用?来表示呢？

生3：其实和分月饼是一样的，刚刚是将月饼平均分成了2份，现在是把每个学具纸平均分成2份，这样每份都可以用?来表示.

师：说得真棒，如果现在问你?表示什么，你会怎么说？

生4：把一个物体平均分成2份，其中1份是它的?.

师：你能结合生活实例说一说，你眼中还有哪些?吗？

学生积极举例，如：将苹果、饼干、铅笔等平均分成2份，其中1份是它的?.

设计意图：数学源于生活，为了帮助学生建立分数概念，教师从学生熟悉的中秋节“分月饼”入手，这样既有效地拉近了学生与数学的距离，又有效地激发了学生学习的积极性.在此基础上，教师引导通过“折一折”“画一画”“说一说”等活动，在不同的学具纸上探索?，这样通过动手实验有效地降低了认知的难度，提升了学生参与的积极性，促进分数概念的建立.

3 巧借“元角分”建立小数概念

“小数的初步认识”以整数的四则运算和分数的认识为基础，它既是数的又一次扩展，也是沟通整数和分数的桥梁.其实在生活中小数也是随处可见，虽然小学生生活经验有限，但是他们大多对小数并不陌生，有很多学生在学习小数之前就已经会读能写了.不过，学生对小数的认识还是停留在表象，不能理解它的真正意义.小数的认识比自然数的认识更为抽象，若直接讲授可能难以让学生理解和接受.因此，教学中应以学生熟悉的具体情境为切入点，借助数学模型让学生在实验操作中理解小数的意义，建立小数的概念.

案例3：认识“0.5”

师：这个是某超市文具柜台的部分商品的单价.（教师PPT出示商品清单）

师：这支铅笔的单价是0.5元？如果我要买一支铅笔要付多少钱呢？

生齐声答：5角.（师板书：5角=0.5元）

师：之前我们已经学过了元角分，请大家回忆一下，元与角有什么关系？

生1：1元=10角，它们之间的进率是10.

师：很好，如果用分数来表示5角你会吗？

生2：5角就是5/10元.（教师继续板书：5角=5/10元=0.5元）

师：5/10元如何理解？

生2：就是将1元平均分成10份，它代表其中的5份.

师：那0.5元可以如何理解呢？

生3：就是将1元平均分成10份，其中的5份就是5/10元，也就是0.5元.

师：现在我们理解了0.5元，思考一下，0.5表示什么呢？请大家在纸上画一画、说一说.

学生积极动手实验，根据分数的学习经验，大家画出了不同形状、不同大小的图形，如正方形、长方形等，将图形分别平分成10份，然后对其中5份进行标注.

师：结合刚刚的实验过程说一说，0.5表示什么？

生4：0.5表示5/10.

师：0.1、0.2、0.8、0.6都是一位小数，如果让你从中选择一个最重要的，你想选哪一个呢？

生齐声答：0.1.

师：为什么？

生5：其他一位小数都是由几个0.1组成的，如0.2中有2个0.1；0.8中有8个0.1.

师：大家太厉害了，一位小数的计数单位被你们这样轻而易举地发现了.

设计意图：从学生已经建立的元角分数学模型出发，让学生结合分数的学习经验将分数与小数建立联系，理解了0.5元的意义.接下来通过动手实验将小数转化为直观图形，这样大大降低了思维的难度，让学生在自主探究中理解了小数抽象的意义，发展了学生自主学习能力^［3］.

总之，在教学“数的初步认识”时，教师要从学生已有的生活经验出发，借助一些已建立的数学模型将抽象的知识直观化，以此降低思维的难度，提升课堂参与度，并让学生在积极参与中理解数的意义，逐渐建立数的概念.

参考文献：

［1］马云鹏.深度学习的理解与实践模式——以小学数学学科为例［J］.课程.教材.教法，2017（4）：6067.

［2］邱思敏.借助情境教学，打造智慧课堂——小学数学情境教学淺析［J］.数学大世界：下旬，2021（6）：59.

［3］李新.夯实分数初步认识提高数学抽象能力——基于2020年江苏省小学数学学业质量监测数据的分析［J］.小学数学教育，2022（2）：810.