外辐射源雷达系统多站接收优化部署方法

杨遵立,董鹏曙,张 衡,卢 浩,喻晨龙

(空军预警学院,湖北 武汉 430019)

0 引言

外辐射源雷达具有低成本、抗电子侦察能力好、反隐身潜力好、抗干扰能力强等突出优点[1-3],是当前雷达技术领域的一个热点。随着广播、电视、移动通信、导航和通信卫星的快速发展,外辐射源雷达的空域探测和覆盖得到广泛研究[4]。文献[5]提出了基于圆阵天线的飞艇载外辐射源雷达系统,分析了其探测范围;文献[6]设计了基于双频地面数字多媒体广播(digital terrestrial multimedia troadcast,DTMB)信号进行探测的小型宽带外辐射源雷达系统;文献[7]针对双基地雷达探测面积影响因素进行了一定分析;文献[8]引入粒子群算法对双基地雷达探测性能评估提出一种改进方法;文献[9]针对双基地雷达的探测范围、测量精度和分辨力等主要性能进行了分析与研究;文献[10]提出一种外辐射源雷达探测范围快速计算方法。以上这些文献,主要针对单个接收站的外辐射源雷达场景进行研究。实际在单站接收场景中,目标探测范围受限。为了进一步增大探测范围,本文在单站接收基础上,对1个照射源和多个接收站构成的外辐射源雷达系统进行研究。在多站接收场景下,照射源可与任意一个接收站配对形成外辐射源雷达,进而构成外辐射源雷达系统。通过接收站位置的优化部署,获得更大的系统探测范围,可进一步提高其探测效能。

1 外辐射源雷达探测原理

外辐射源雷达利用第三方发射的电磁波信号作为照射源来探测目标,选取合适的辐射源与接收天线可构成预警监视系统。发射站、接收站和运动目标构成的外辐射源雷达在平面上的几何结构[5]如图1所示。图中A和B分别表示该雷达的发射站和接收站,L为基线距离,v为探测目标移动速度,φ表示目标速度方向与双基地角β平分线的夹角,Rt和Rr分别为发射站和接收站到目标的距离,θt和θ分别表示为双基地平面上以发射站和接收站为坐标原点时的方位角,也称为外辐射源平面上的目标视角。β=θ-θt为双基地角,它是以目标为顶点,发射站、接收站与目标连线之间的夹角。

图1 外辐射源雷达基本几何结构图Fig.1 Basic geometric structure of passive radar

由余弦定理可得

(1)

设R为双基地雷达的距离和,表示如下:

R=Rt+Rr,

(2)

代入式(1)可得

(3)

双基地雷达探测中,目标到照射源和接收站之间距离和R构成的等距离和椭圆曲线,再由椭圆与接收天线的指向的交点位置,便可进行目标定位。

外辐射源雷达本质是收发分置双基地雷达,其探测威力可由距离积方程[10]表示:

(4)

式(4)中,Pt为外辐射源雷达的发射功率,Gt为发射天线增益,Gr为接收天线增益,λ为外辐射源波长,σB(β)为目标散射截面积,Ft和Fr为方向图传播因子,g为积累增益,k为波耳兹曼常数,TS为接收机噪声温度,Bn为接收机检波器前的噪声带宽,Fn为雷达系统噪声系数,(S/N)omin为接收机输出端最小可检测信噪比,Lt和Lr分别是发射和接收系统损耗,探测常数b为等效单基地雷达时最大探测距离。

2 外辐射源雷达优化方案

2.1 单站接收情形下外辐射源雷达优化方案

假设单部外辐射源雷达部署如图2所示,照射源和接收站的位置分别为原点(0,0)和(L,0),探测范围满足卡西尼卵形线表示为

图2 单站接收时外辐射源雷达部署示意图Fig.2 Deployment based on onereceiving station

(x2+y2)2·((x-L)2+y2)2=b4。

(5)

在外辐射源雷达技术参数确定的条件下,其探测范围主要由探测常数b、基线距离L、目标角度等因素决定[11]。当基线距离L为零时,退化为单基地雷达,其探测范围是半径为b的圆。随着基线距离的增大,其探测范围由椭圆形逐渐变为哑铃形、伯努利双纽形,直至分裂为两个离散的区域。

设m为基线距离和探测常数的比值表示为

m=L/b。

(6)

当m=0时,探测范围为以b为半径的圆;当02时,探测范围为2个相离的区域[10]。

假设外辐射源雷达覆盖范围的面积为S1,其与探测常数b、基线距离L有关,该函数是隐函数,可表示为

S1=f(b,L)。

(7)

以覆盖范围面积最大为优化准则,单站接收外辐射源雷达部署优化模型为

(8)

由于探测常数b可由式(4)唯一确定,式(8)即以基线距离L为参变量求取覆盖面积最大值。

为了表征外辐射源雷达覆盖的通用性,定义单站接收场景下的归一化的探测覆盖面积为

S1n=S1/(πb2)。

(9)

采用积分法可以求出探测覆盖面积值并进行归一化处理得S1n和m的变化曲线如图3所示。

图3 单站接收时外辐射源归一化探测覆盖面积Fig.3 Normalized coverage area of one receiving station

在系统参数不变的条件下改变基线距离(改变m值)可确定单源照射下外辐射源雷达优化部署方式。可以发现,单站接收场景下,外辐射源雷达覆盖特性由基线距离L决定,可得如下结论:

1) 单基地雷达的覆盖面积最大(归一化面积为1),其探测覆盖面积始终优于双基地雷达;随着基线距离L的增加,双基地雷达覆盖面积单调减小。

2) 当基线距离L在0～1.5b之间时,归一化覆盖面积变化不大(1.0～0.92);当L在1.5b～3.0b之间时,随着L增加归一化面积迅速下降(0.92～0.23)。

2.2 多站接收情形下外辐射源雷达优化方案

当有n个接收站与1个照射源构成外辐射源雷达系统时,设总的覆盖面积为Sn,类似于单个外辐射源雷达,该探测面积可以表示为基线距离L和探测常数b的函数,表示如下:

Sn=fn(b,L1,L2,…,Ln)。

(10)

基线距离(L1,L2,…,Ln)分别为接收站B1,B2,…,Bn到照射源之间的距离。

假设照射源位于原点,n个接收站的位置分别为(c1,d1),(c2,d2),…,(cn,dn),式(10)中的面积是如下方程组围成的总面积之和:

(11)

Sn通过积分法求解,可以用每个外辐射源雷达的覆盖面积之和减去相互重叠部分,表示如下:

(12)

式(12)中,Ai表示发射源和第i个接收站组成的外辐射源雷达的探测覆盖面积,∩AiAj表示区域Ai和Aj之间相交的公共面积,∩AiAjAk表示发射源和Bi,Bj,Bk3个外辐射源雷达区域的三者相交的公共面积,∩A1A2…An表示n个区域的相交的公共面积。

定义mn=Ln/b为基线距离Ln和探测常数b的比值。类似单站接收场景,多站接收场景中仍以覆盖范围面积最大为优化准则,优化部署模型为

(13)

式(13)中,m=(m1,m2,…,mn)为n维向量,在满足探测距离要求情况下,求取探测覆盖面积最大值。

为了表征外辐射源雷达覆盖的通用性,定义多站接收场景下的归一化的探测覆盖面积为

Snn=Sn/(πb2)。

(14)

多站接收情形下的外辐射源雷达系统优化的目的是通过调整接收站的位置,满足探测距离的条件下,使得系统总覆盖面积最大。为了简化分析,在下文仿真中假设照射源与n个接收站之间的基线距离相等均为L,通过计算探测覆盖面积和基线距离L的关系,优选接收站的最佳部署位置。

3 实例及仿真验证

以FM调频广播作为外辐射源,计算系统探测距离。设接收机端最小可检测信噪比(S/N)omin、发射功率、发射和接收天线增益、FM信号工作频率、有效工作带宽、目标散射截面积、相干积累增益、方向图因子、系统噪声系数、系统总损耗等参数见表1所示,可计算得系统探测常数b为262.3 km。

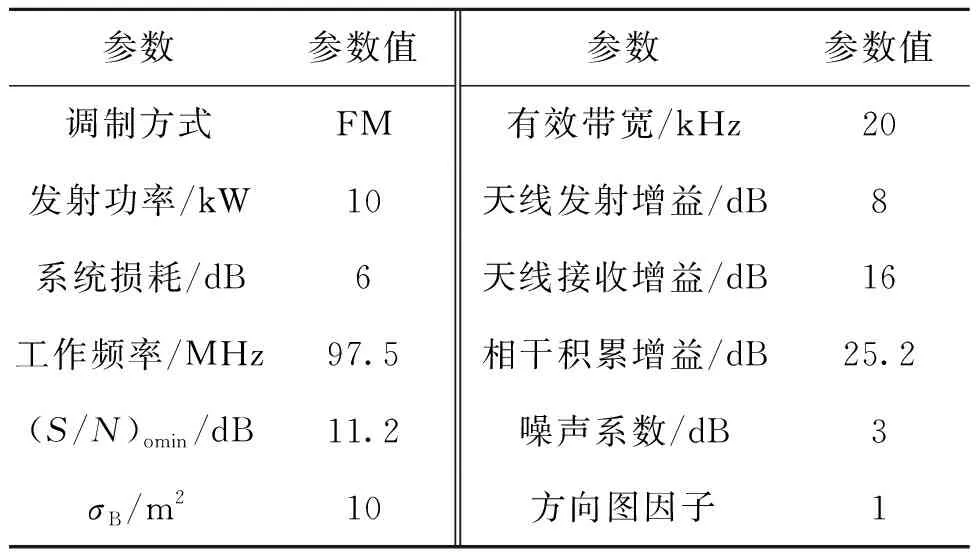
表1 FM外辐射源雷达系统参数Tab.1 System Parameters of FM Passive Radar

3.1 双站接收情形下的外辐射源雷达优化部署

按图4进行双站接收场景下外辐射源雷达部署,假设发射站部署在原点,2个接收站B1和B2关于x轴对称,2个接收站到发射站的距离均为基线距离L,接收站之间的距离为2d(分别取为100,200,300,400 km)。

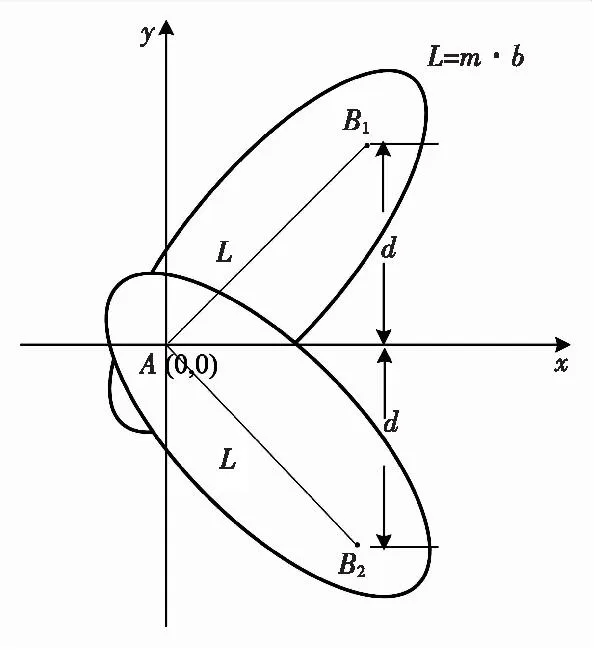
图4 双站接收时外辐射源雷达部署示意图Fig.4 Deployment based on two receiving stations

图5是不同m值下的探测范围示意图,初始值m=d/b时,2个接收站位于y轴上,其与发射站组成的覆盖区域均为近似椭圆;当d/b2时,覆盖区域均为2个相离区域。基于m的变化范围,用积分法可求出双站接收场景下的探测覆盖面积。

图5 双站接收时外辐射源雷达探测范围分析Fig.5 Detection coverage analysis of two receiving stations

图6为不同接收站距离(2d分别取为100,200,300,400 km)下,仿真计算出的归一化探测覆盖面积S2n的曲线图。由于初始值m=d/b,在不同d取值下初始值m是不同的。

图6 双站接收时外辐射源雷达归一化探测覆盖面积Fig.6 Normalized coverage area of two receiving stations

在系统参数不变的条件下改变接收站位置,以双站接收场景下的外辐射源雷达探测覆盖面积最大为优化标准,得到不同接收站距离下的外辐射源雷达系统最优部署方式,如图7所示。

图7 双站接收时外辐射源雷达优化部署Fig.7 Optimal deployment of passive radar based on two receiving stations of different distances

综合图6和图7,双站接收的覆盖特性由接收站间距离d和基线距离L共同决定,可得如下结论:

1) 双站接收条件下,外辐射源雷达最佳基线取值范围是0.5b～1.5b,其归一化覆盖面积变化不大。

2) 双站接收条件下,当两个接收站之间的距离小于b时(2d取值100,200 km),其最大归一化覆盖面积较小(取值1.12,1.23);当两个接收站的距离为b～1.5b(2d取值300,400 km)时,其归一化覆盖面积较大(取值1.34,1.43);当两个接收站的距离大于1.5b时,其归一化覆盖面积随着两个接收站之间距离的增大而增大,但增速变缓,导致x轴正方向前向探测距离变短,出现探测盲区。

3) 双站接收条件下,综合考虑接收站尽可能前置部署、归一化覆盖面积大的要求,两个接收站之间的距离建议b左右(300 km约为1.14b)为宜。

3.2 三站接收情形下的外辐射源雷达优化部署

按图8进行三站接收场景下外辐射源雷达部署,假设发射站位于原点,接收站B1和B2关于x轴对称,B3部署在x正半轴,接收站B1和B2到B3所在x轴的垂直距离都为d(分别取100,200,300,400 km),假设照射源A到接收站B1,B2,B3的距离均为基线距离L。

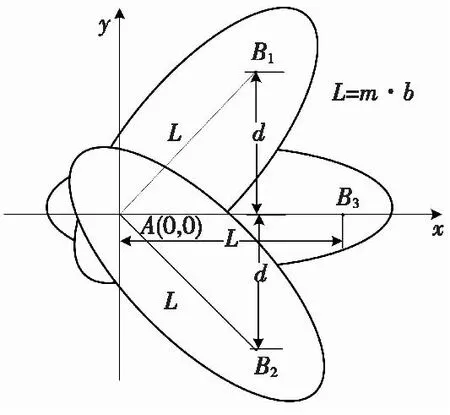
图8 三站接收时外辐射源雷达部署示意图Fig.8 Deployment based on three receiving stations

图9为不同m(m=L/b)值下的探测范围的示意图。初始值m=d/b时,B1和B2接收站位于y轴上,其与发射站组成的覆盖区域均为近似椭圆,且关于x轴对称,B3位于原点和发射站位置重合,其覆盖范围为以b为半径的圆;当d/b2时,3个接收站与发射站覆盖区域均为2个相离的区域。基于m变化范围,用积分法可求出三站接收下外辐射源系统总的探测覆盖面积。

图9 三站接收时外辐射源雷达探测范围分析Fig.9 Detection coverage analysis of three receiving stations

用积分法求出三站接收下的外辐射源系统总探测覆盖面积,归一化处理后得S3n,如图10所示,为仿真计算出的不同接收站垂直距离(d分别取为100,200,300,400 km)下的归一化覆盖面积曲线图。

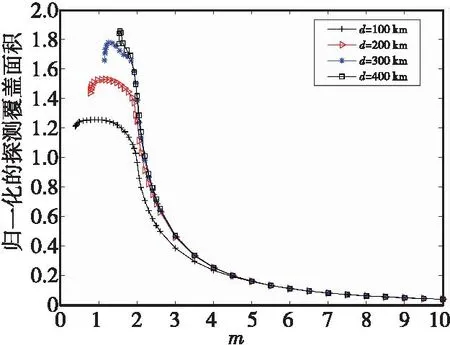
图10 三站接收时外辐射源雷达归一化探测覆盖面积Fig.10 Normalized coverage area of three receiving stations

在系统参数不变的条件下改变接收站位置,以三站接收场景下外辐射源雷达探测覆盖面积最大为优化标准,得到外辐射源雷达系统最优部署方式,如图11所示为d分别取100,200,300,400 km时优化部署时探测面积的覆盖场景图。

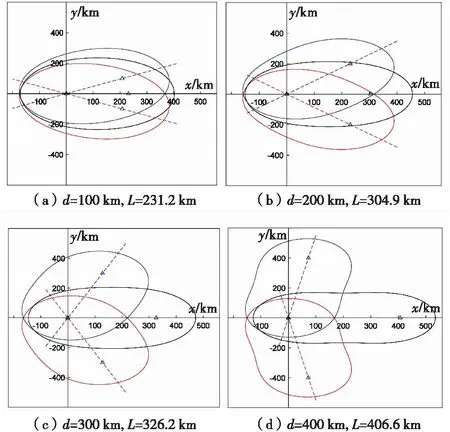
图11 三站接收外辐射源雷优化部署图Fig.11 Optimal deployment of passive radar based on three receiving stations of different distances

仿真发现,三站接收场景下探测覆盖特性由接收站之间垂直距离d和基线距离L决定,可得如下结论:

1) 外辐射源雷达最佳基线距离L取值范围是b～1.8b,其归一化覆盖面积变化不大,值都较大;当L大于1.8b时,随着L的增加,归一化覆盖面积迅速减小,综合考虑接收站尽可能前置部署、归一化覆盖面积大的要求,建议L取值范围为b～1.8b。

2) 3个接收站之间的垂直距离小于b(d取值100,200 km)时,其归一化覆盖面积值较小((取值1.26,1.53);当3个接收站之间垂直距离d为b～1.5b(d取值300,400 km)时,其归一化面积值较大(取值1.78,1.86);当3个接收站之间垂直距离大于1.5b时,其归一化覆盖面积随着垂直距离d的增大而增大,但增速明显变缓,同时在靠近x正半轴第一、第四象限区域中,存在探测距离小于1.5b的盲区。

3) 综合考虑接收站尽可能前置部署、归一化覆盖面积大的要求,3个接收站之间的垂直距离d以b左右(300 km约为1.14b)为宜。

当接收站为3个以上时,只要接收站部署场景确定,以积分法求出探测覆盖面积,以系统覆盖面积最大为优化标准,利用计算机仿真同样可以确定接收站的最优部署位置。

4 结论

本文以归一化的探测覆盖面积为优化标准,对基于多站接收的外辐射源雷达优化部署展开了研究,进行了探测范围、归一化探测覆盖面积和优化部署场景的仿真。仿真分析表明,通过多站接收场景下接收站优化部署,可以有效增大系统覆盖范围,提高系统探测效能。本文只讨论了单个照射源场景下的多个接收站的外辐射源雷达的优化部署,在其他优化标准条件下,多源照射多站接收场景下外辐射源雷达的优化部署是下一步的研究方向。