温州软黏土结构性评价及盾构隧道施工扰动研究*

卢生安 王 威 肖 力

(1.温州市铁路与轨道交通投资集团有限公司, 浙江温州 325003; 2.浙江大学滨海与城市岩土工程研究中心, 杭州 310058)

温州地铁工程埋深范围内的地基土属典型的海积、冲海积、滨海沼泽相淤泥质土,与上海、杭州、宁波等地区相比,其含水量更高(高达70%)、灵敏度更高、触变性更大、土的抗剪强度和渗透性更低、变形性和压缩性更高。采用盾构法施工往往会引起盾构隧道周围土层的扰动,产生相当大的工后附加沉降,影响盾构隧道及周边建、构筑物的长期服役性能。明确盾构隧道施工对地层的扰动影响,准确快速预测扰动所带来的附加沉降量,有助于盾构隧道在建设过程中采取相应的设计和施工方法来保证其安全性和耐久性。

土的结构是土粒或团粒(几个或多个土颗粒联结成的集合体)在空间的排列和它们之间的相互联结。[1-2]天然土在沉积过程中和沉积后受到不同的地质条件、沉积环境、触变硬化、淋溶、胶结等物理化学作用,因而表现出异于重塑土的力学特性。[3-5]而原状土的力学特性不同于重塑土的复杂因素通常被归结为土的结构性影响。[3-4]大量工程经验[6-8]表明:施工扰动越大,附加沉降越大。同时,大量室内试验均发现扰动会导致结构性土屈服应力减小,压缩性增大。[9-12]这表明扰动会导致结构性土体内部结构和应力状态发生改变,宏观表现为压缩性增大、强度降低,工程性质相对于原状土较差,因此客观评价土体结构性以及扰动对结构的影响对于工程建设有着重大的意义。

土体的扰动是指外界作用引起土的应力释放,体积、含水量或孔隙压力的变化,以及结构性或组构的变化。[13-15]李涛等认为定量评价扰动度的物理力学指标须要满足有明确物理意义、对扰动敏感、易量测或推算的条件。[16]许多学者采用不同的物理力学性质指标建立了土体扰动度评价方法并且给出了受扰动后力学参数变化量与扰动度之间的关系。Ladd等认为:饱和土样的不排水模量受土体扰动最为敏感,采用不排水模量的变化来评价土体扰动程度。[17]Chen等在杭州湘湖地铁车站倒塌的基坑周围做了大量的静力触探试验和十字板剪切试验,认为扰动度是土体不排水抗剪强度的衰减率。[18]徐永福等认为:超孔压较大的情况下,土体结构发生破坏,结构强度丧失,因此提出以竖向有效应力的改变程度(即应力扰动度)来衡量盾构开挖引起土体的扰动程度。[19]王军提出以不排水强度特征量来定量评价土体扰动程度的方法。[20]但以上评价指标都是基于现场试验以及室内试验,无法提前预测盾构施工扰动周围土层的规律。孙钧等认为土体受扰动的影响主要反映在土体应力、应变及其力学性状的变化,可以采用剪应变的变异来定量识别。[21]Meng等从剪应变的角度来描述土体受扰动的程度,定义扰动度是土体受施工扰动产生的剪应变与破坏剪应变的比值,研究了不同施工参数对宁波黏土的扰动的影响。[22]

以上研究往往针对于有一定沉积历史的超固软弱黏土,但对欠压密的软黏土并未进行深入研究。因此,基于温州市轨道交通M1线某区段的盾构隧道施工的工程背景,通过研究评价该区域软弱黏土的力学性状和结构性,建立地层-盾构隧道三维弹塑性有限元模型,研究盾构隧道施工对地层的扰动规律以及扰动度分布,计算施工引起的地表附加扰动沉降,对有效预测类似工程案例的扰动影响有一定的参考价值。

1 土样特性

土样取自温州市轨道交通M1线温州北站至金穗路站段的淤泥土层,在轨道两侧轨顶面线标高内选取8组代表性断面,钻孔编号依次为Z1、Z2、Z5、Z6、Z11、Z12、Z15、Z16,取样深度基本位于距地表10 m左右范围。为尽量减少对土样的扰动,采用高度为30 cm,直径为10 cm的薄壁取土器进行取样,通过千斤顶和反力架组成的推土器将土推出,在温州大学开展基本物理性质试验。其中,液塑限试验采用液、塑限联合测定仪法,试验步骤参照GB/T 50123—2019《土工试验方法标准》。

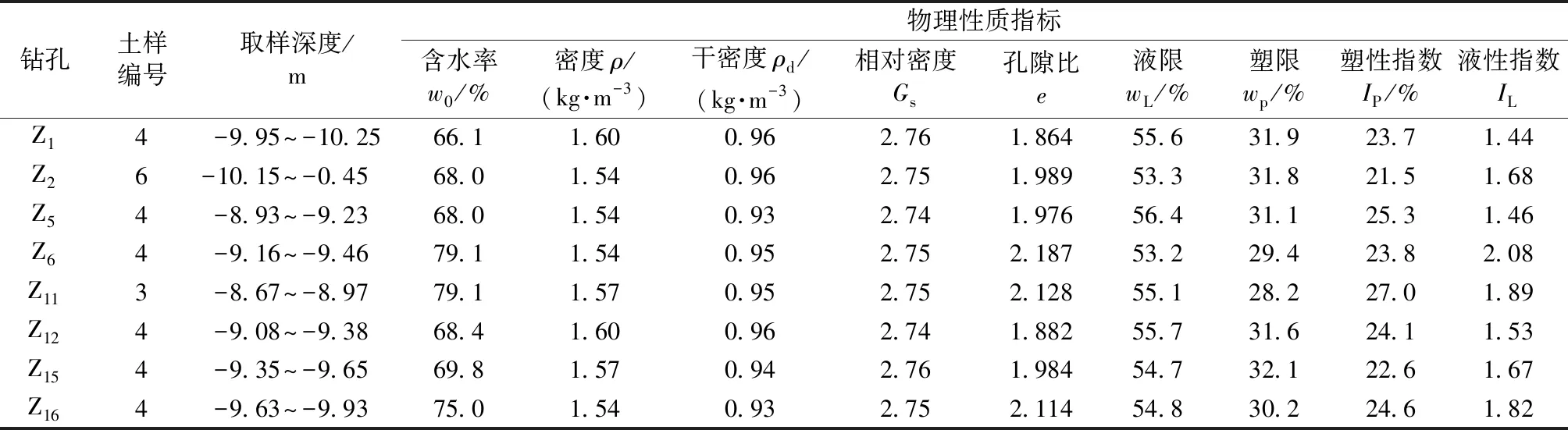
表1 土体基本物理性质指标

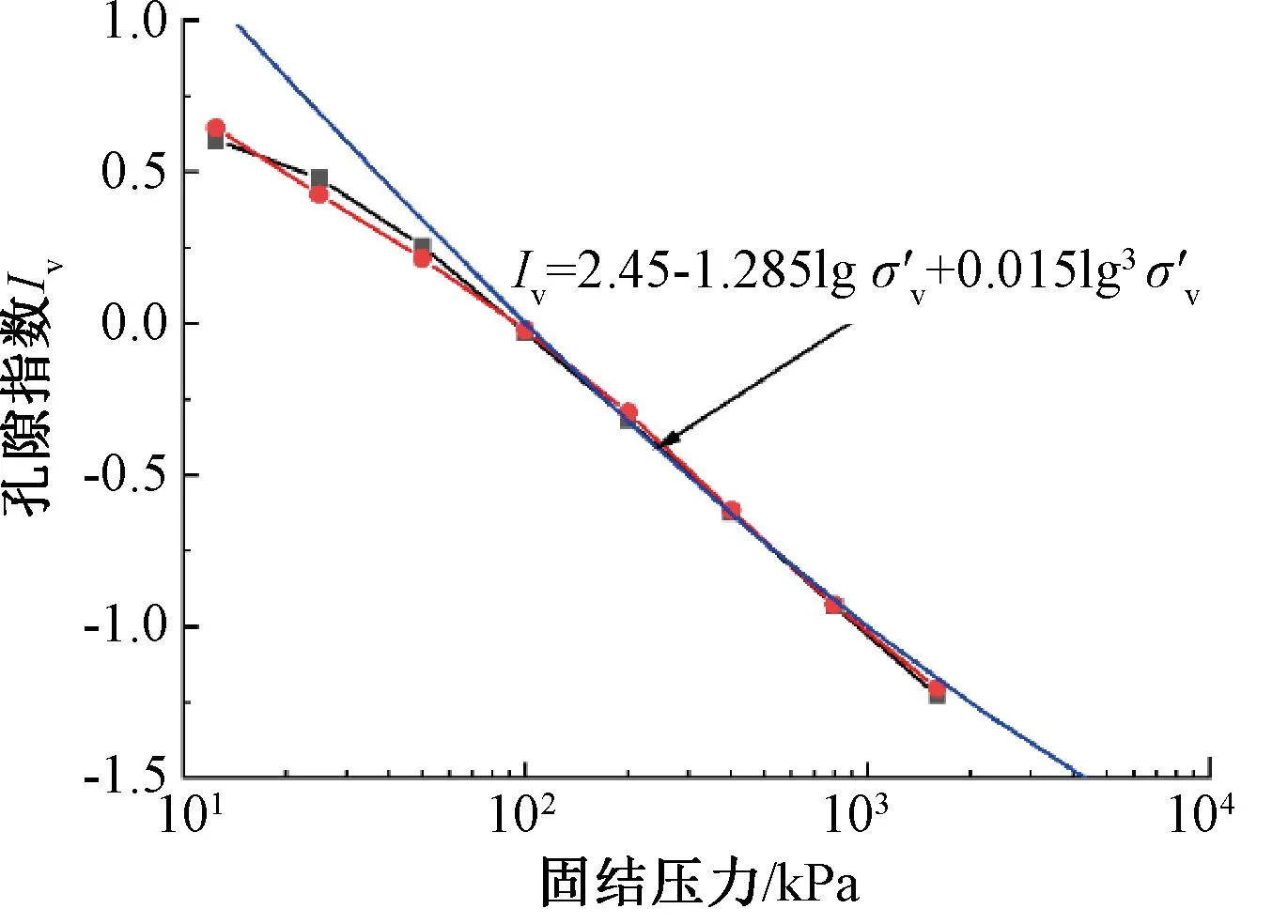
表1是土样的基本物理性质指标,Z1、Z2、Z5、Z12、Z15等5个孔位土样含水率接近70%,而Z6、Z11、Z16则接近80%。8个孔位土样的干、湿密度,相对密度孔隙比十分接近。图1反映了土样的稠度状态,土样基本位于A线附近,B线以右。

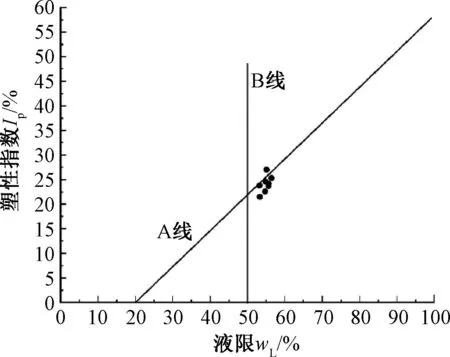
A线:Ip=0.73(wL-20); B线:wL=50%。

2 一维压缩性状

(1a)

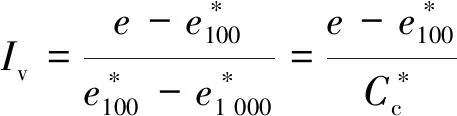
(1b)

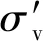
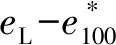
(2a)

(2b)

其中eL=GswL

式中:eL是黏土液限的对应孔隙比。

3 结构性评价

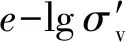
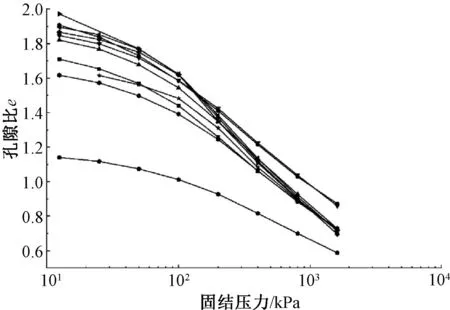
许多学者通过对结构性土的一维压缩试验发现:结构性强的土均具有较明显的结构屈服应力,当固结应力小于屈服应力时,其压缩曲线较为平缓,压缩性较小;当固结应力大于屈服应力时,压缩曲线会出现骤降,压缩性急剧增大;最后随着固结应力的不断增大,其压缩曲线最终会趋向于重塑土的压缩曲线。因此,结构屈服应力是评价土体结构性的重要参数。

Burland提出将结构屈服应力与自重有效应力的比值定义为屈服应力比[5],陈云敏将其定义为结构稳定系数[24],可以说明该比值能够反映土体的结构强度强弱:

ηYSR=pc/p1

(3)

其中p1=∑γ′h

式中:ηYSR为屈服应力比;pc为土体的结构屈服应力;p1为土体的有效上覆应力,γ′和h分别为土层的有效重度和厚度。

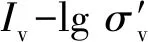
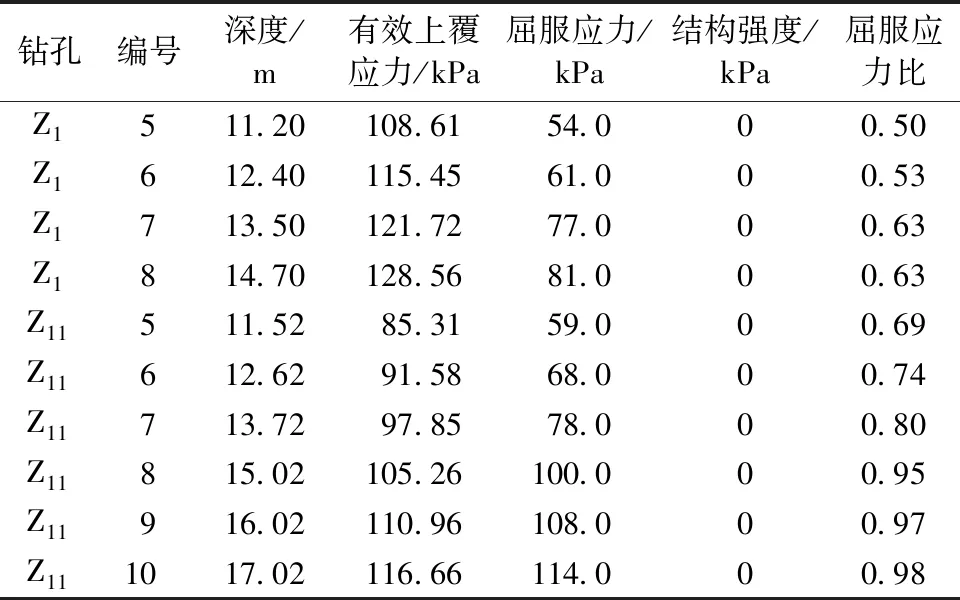
表2 土样结构强度参数

Cotecchia 等提出了灵敏度架构的概念[28],用以比较原状天然结构土与重塑土之间的力学行为。灵敏度可以作为黏土结构性的直接评价方法,如上述的无侧限抗压强度灵敏度。Chandler基于Burland的固有压缩曲线理论提出了用应力灵敏度来反映原状土相较于重塑土的结构抗力。[11]应力灵敏度是原状土的屈服应力与屈服孔隙比下固有压缩曲线所对应的竖向有效应力的比值:

(4)

图5 应力灵敏度

表3是各土样应力灵敏度计算结果,结合表中计算结果来看,各土样的应力灵敏度在9.56～43.19的范围内(除Z11-10外),均大于天然正常固结土的应力灵敏度,说明该土样在加载过程中比天然沉积土有更高的结构附加抗力,这是由于该土样具有较强的结构性所致。而随着土样所承受固结压力的不断增大,压缩曲线逐渐趋近于固有压缩曲线,表明随着固结压力的不断增大,土体的结构性逐渐遭到破坏,压缩性不断增大,压缩曲线最终趋近于重塑土。

表3 土样应力灵敏度

4 三维有限元模型分析

4.1 地层分布

温州市轨道交通M1线温州北站—金穗路站段盾构隧道中心埋深16～20 m,该段局部地表填土较厚,最大埋深可达23 m左右。场地内的软土主要为上部淤泥和淤泥质黏土,呈流塑状,该类土层具低强度、高含水量、高压缩性,有较明显的蠕变、触变特性,分布广泛而连续,厚度一般较大。盾构隧道主要穿越淤泥质土。该层抗剪强度低,灵敏度高,施工扰动后强度骤降,自稳性能差。地层分布断面如图6所示。

4.2 有限元模型概况

选取温州北站至金穗路站区间的某段65 m长的区间作为研究对象,采用PLAXIS 3D对该区段的盾构施工进行数值模拟。模型中包括土层、盾构机外壳、盾尾、盾构隧道衬砌以及开挖面,如图7所示。为简化计算,假定该区段地层均为水平层状,区间盾构隧道上覆土层平均厚度为12.18 m。参考宁波桃渡路—鼓楼区间盾构机[29]的外形尺寸,衬砌管片幅宽为1.2 m,外径为6.2 m,内径为5.5 m,盾构机全长为8.4 m(相当于7个衬砌环)。为考虑盾构机锥筒形所引起的地层变形,盾构前6环按照-0.694‰的线性收缩率向盾尾逐渐收缩,实现盾构机锥形最大收缩率为0.5%。盾构机第7环设置面收缩来考虑盾构施工引起的地层损失。为消除边界效应对计算结果的影响,考虑影响范围4～6倍的隧道直径,地层模型x、y、z向的尺寸分别取60,150,60 m,其中x方向为垂直于盾构隧道轴线的横向方向,y方向为盾构隧道轴向方向,而z方向为竖向。模型顶部为自由边界,侧边界采用动铰支座约束,底边界采用固定铰支座约束。盾构开挖面、盾尾和盾壳均采用不排水界面。混凝土衬砌和土层采用10结点楔形实体单元模拟,盾构机外壳采用6结点板单元模拟,盾构机与周围土层之间的相互作用采用12结点的界面单元来模拟。考虑到模型为对称结构,因此取1/2模型进行分析。

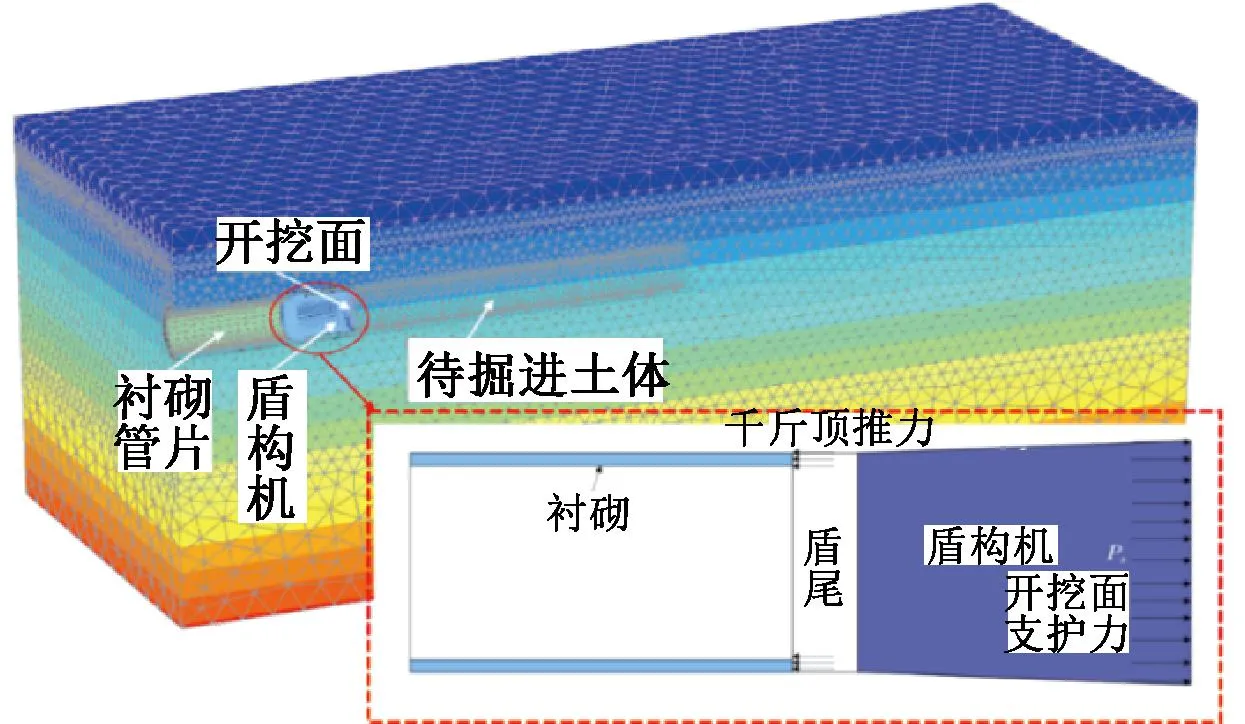
图7 盾构隧道开挖模拟有限元数值模型

4.3 有限元模型参数取值方法

盾壳和衬砌采用各向同性线弹性模型,不考虑塑性变形,支护结构材料参数见表4。盾构隧道开挖卸荷区域的软土层(②1)采用小应变硬化模型(HSS model)来模拟土的应力-应变关系。HSS模型在HS模型的基础上不仅可以考虑剪切硬化和压缩硬化,同时还考虑土体小应变刚度特性,而且增加了对土体小应变情况下的剪切模量衰减行为的考虑。因此,HSS本构模型能够更好地适用于敏感环境下盾构隧道开挖对周围土层影响的数值分析。其他软土地层(①、③1)采用硬化土模型(HS model),盾构隧道上部的填土和下部相对强度高的卵石采用摩尔-库仑来模拟。以上模型的参数根据地勘报告并结合文献[30]进行取值。土层材料参数见表5所示。

表4 支护结构材料参数

表5 土的物理力学参数

4.4 有限元模型工况模拟

在盾构掘进的过程中,开挖面支护力是施工控制参数。根据杭州地区的盾构开挖实测数据,开挖面支护力与理论计算的静止土压力比值为1.16～1.74,呈梯形分布。模拟中取开挖面支护力与静止水土压力的比值为1.5。盾尾注浆率Gr是通过在盾构机最后一环设置收缩率Cg来进行模拟,《PLAXIS 3D 2018参考手册》[31]给出收缩率Cg的大小是相对于盾构隧道截面积改变率的一半。根据一般工程经验,盾尾间隙一般是盾构隧道截面积的2%[32]。因此,注浆率Gr和衬砌收缩率Cg的关系如式(5):

Gr=(1-100Cg)×100%

(5)

根据宁波地铁1号线现场实测数据,一般地表沉降从距离该断面3D(D为隧道直径)开始发展,盾构掘进开挖面通过6D后逐渐稳定。依据Meng数值模拟的分析结果[22]设置,在数值模拟中详细模拟盾构掘进开挖10D(51环衬砌)的过程。将观察面设置在距离初始开挖面4D的位置,如图8所示。通过A—A断面随盾构施工掘进的力学响应来总结盾构掘进施工对地层的扰动规律。盾构施工掘进有限元模拟过程如表6所示。

表6 盾构施工掘进数值模拟步骤

图8 盾构掘进分析模型示意 m

5 模型计算结果分析

5.1 地表沉降分析

图9分别是盾构机到达B—B断面时盾构隧道轴线上方地表纵向沉降曲线以及开挖面后方的横向沉降槽曲线。从图9可以看出:盾构开挖面上方土体表现出轻微沉降(约为5 mm),而开挖面前方一定距离的土体在支护力的作用下发生隆起,其影响范围大致在4D左右。开挖面后方地表沉降迅速发展,直到一段距离后地表沉降开始逐渐减小,随后趋于平缓。这是由于盾构机质量较大,造成周围土层出现了一定的沉降变形,而管片远轻于开挖土体和盾构机的质量,盾构机离开后出现了一定程度的回弹。随着盾构机的远离,地表沉降变化趋于平缓。图9a表明,当盾构机到达B—B断面后,A—A断面的地表沉降已基本稳定,盾构机的继续开挖对该断面几乎没有影响,因此可以表明盾构机的开挖作用对该断面不再造成扰动。此时施工沉降达到了最大值,约27.2 mm。

a—地表纵向沉降; b—开挖断面地表横向沉降槽。

5.2 盾构施工扰动规律

一般来说,盾构隧道轮廓线周围土体与盾构距离较近而受到最为剧烈的扰动,可以认为该位置的土体已完全扰动成为重塑土,扰动度达到了100%。因此将盾构隧道轮廓线周围土体在盾构施工时的最大剪应变视为临界剪应变,扰动度的计算式如式(6):

ηsd=γs/γc

(6)

式中:γs为盾构隧道施工引起的剪应变大小;γc为临界剪应变。

图10是盾构隧道施工掘进过程数值模拟中监控断面A—A扰动区的发展演变过程。以盾构掘进的方向为正方向,距离监控断面A—A的环数来表示盾构开挖面的位置。将扰动的发展分为三个阶段,即初步发展阶段、快速发展阶段以及稳定阶段。初步发展阶段是指开挖面尚未达到监控断面,在这一阶段,盾构隧道周围地层初步发展,主要是由于支护力的扰动作用。从图10可见:当开挖面距离监控断面-3环时,扰动开始发展,但仅仅局限于拱顶位置,这是由于拱顶位置的围压相对于拱底和拱腰位置较小,在开挖面支护力的作用下,产生了更大的正超静孔隙水压力,从而破坏了土颗粒之间的联结,更容易形成扰动。当盾构机进一步掘进时,拱顶、拱底以及拱腰位置均有所扰动。总体而言,初始阶段扰动范围较小,扰动程度不大。当开挖面达到监控断面后,开始进入快速发展阶段,快速发展阶段是指盾构机身逐渐经过监控断面的过程。在这一阶段中,扰动主要是由于盾构机身呈锥形导致的卸荷所引起的。扰动范围快速发展,扰动区在竖向和水平向都有明显的扩张,扰动区形状由初始的圆形逐渐变成“眼睛”形(水平向范围大于竖向范围)。在这一过程中,扰动程度也得到了一定的发展,但增长量并不大。第三阶段是指盾构机身离开监控断面的过程。当盾尾达到监控断面时,扰动范围达到了最大,扰动程度剧烈上升,这是由于卸荷和注浆共同发挥作用所导致的,其形状仍呈现“眼睛”形,但扰动程度相较于第二阶段有了明显的增大。随后,扰动发展逐渐稳定,扰动程度和扰动范围只有小范围的增大,这是由于盾构机远离监控断面所引起的。当开挖面通过13环后,扰动已不再发展。

图10 盾构施工掘进过程周围土层扰动发展

从扰动的来源来看,扰动范围主要由开挖面支护力和卸荷作用所决定,而扰动程度主要受卸荷和注浆作用所控制。图11是扰动区的纵断面,可以发现:开挖面支护力对土体的扰动延伸至开挖面前方0.8D,在横断面上扰动范围得到初步发展,由于卸荷作用,盾构机身周围土层的扰动范围不断增大,最终在盾尾处达到最大值,同时由于盾尾的注浆作用,周围土层的扰动程度急剧增大。

图11 扰动区的纵断面

5.3 扰动度分布

图12是盾构机掘进至B—B断面时监测断面(A—A)的剪应变云以及以剪应变状态作为指标的扰动区形状(ηsd≥10%)。从形状上来看,扰动区形似“眼睛”。扰动区在水平方向延伸至拱腰外侧0.4D,在竖向延伸至拱顶上方0.30D以及拱底下方0.25D,这与Salehnia根据剪应变划分盾构施工在周围地层中造成的破坏区呈“眼睛”形[33]基本一致。

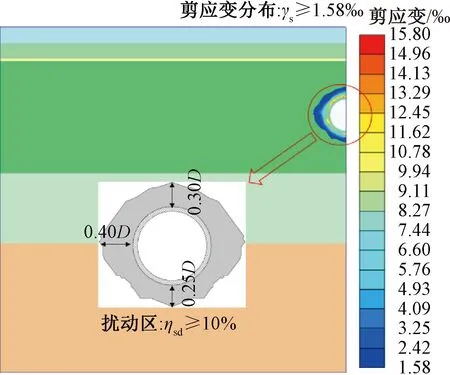
图12 盾构掘进的剪应变云与扰动区形状

为了能够准确地预测施工扰动对地基沉降的影响,根据数值模拟结果得出了以剪应变变异状态为指标的盾构隧道外侧扰动度分布,包括拱顶上方、拱腰外侧以及拱底下方土层,见图13。从图13可见:拱顶上方和拱底下方一定区域的土体扰动度随与盾构隧道距离的增大而逐渐衰减。随着埋深的增大,扰动度衰减速度逐渐变缓,这也符合扰动对土体的影响局限于某一范围内的客观事实。与拱顶上方和拱底下方扰动所不同的是:拱腰外侧扰动度随着与盾构隧道距离的增大而呈现指数衰减,衰减范围大致在1D左右。以上盾构隧道外侧土体扰动度分布拟合曲线方程汇总如表7所示。

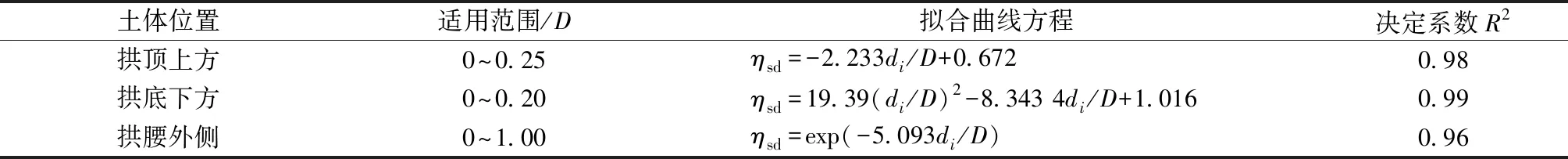
表7 盾构隧道外侧土体扰动度分布拟合方程

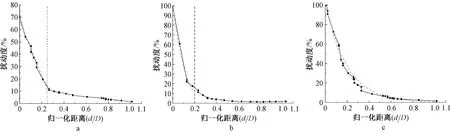
a—拱顶上方; b—拱底下方; c—拱腰外侧。

5.4 扰动沉降计算

扰动后的地基沉降计算需要在变形参数和扰动度之间建立关系,孟凡衍对杭州湘湖地区软黏土的试验结果[31]表明,扰动会引起土体结构性的衰减,土体压缩指数和屈服应力随扰动度的增大而线性下降。扰动后的结构屈服应力可根据Nagaraj等所提出的扰动土结构屈服应力计算式[34]得到:

pcd=(1-ηsd)pc

(7)

式中:pcd为扰动土的屈服应力;pc为原状土的屈服应力。

由于土体压缩指数随扰动度的增大而线性下降,因此假定扰动土的压缩指数的大小介于原状土与重塑土压缩指数之间,即:

Ccd=(1-ηsd)(Cc-Ccr)+Ccr

(8)

式中:Cc为原状土的压缩指数;Ccr为重塑土的压缩指数;Ccd为扰动土的压缩指数。

从式(8)可以观察到:当土体完全扰动,即ηsd=100%时,结构屈服强度变为零,压缩指数变为重塑土的压缩指数,压缩曲线转化为重塑土的压缩曲线。为建立温州扰动土沉降模型,作出以下几点基本假定(图14):

图14 结构性土一维压缩e-lg p曲线

1)原位压缩曲线在e-lgp坐标系内为双折线模型,结构屈服应力前为水平线,即孔隙比e为一常量。

2)原状土、扰动土和重塑土压缩曲线在0.42e0相交,原位压缩曲线采用Schmertmann法[35]进行修正。

3)理想重塑土颗粒之间没有相互作用,固结压力为零,压缩曲线为一直线[24]。

基于上述假定,根据衰减后的压缩参数采用分层总和法计算扰动土的沉降:

(9)

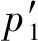
重点研究扰动对软土层压缩的影响,将软土层划分为8层(拱顶上方5层,拱底下方3层)。假定压缩指数与初始孔隙比沿深度方向不发生改变。施工扰动后的地基沉降计算如表8所示:地表施工沉降为-27.2 mm,扰动沉降为-143.21 mm,地表总沉降量为-170.41 mm,超过软土地层中地铁运行的标准(50～100 mm)[36];盾构隧道基底施工沉降为+14 mm(上浮),扰动沉降为-63.82 mm,因此管片表现出下沉,沉降量为-49.82 mm,超过规定的管片沉降报警值(20～30 mm)[36]。由此说明未考虑扰动的施工沉降往往偏于危险,施工沉降的计算必须考虑施工扰动的影响。同时从表中可以看出:扰动沉降主要来源于盾构隧道轮廓线周围的土体,这是由于在施工过程中受到了剧烈的扰动所致,因此有必要对盾构隧道轮廓线周围进行加固,以避免出现过大的扰动沉降。

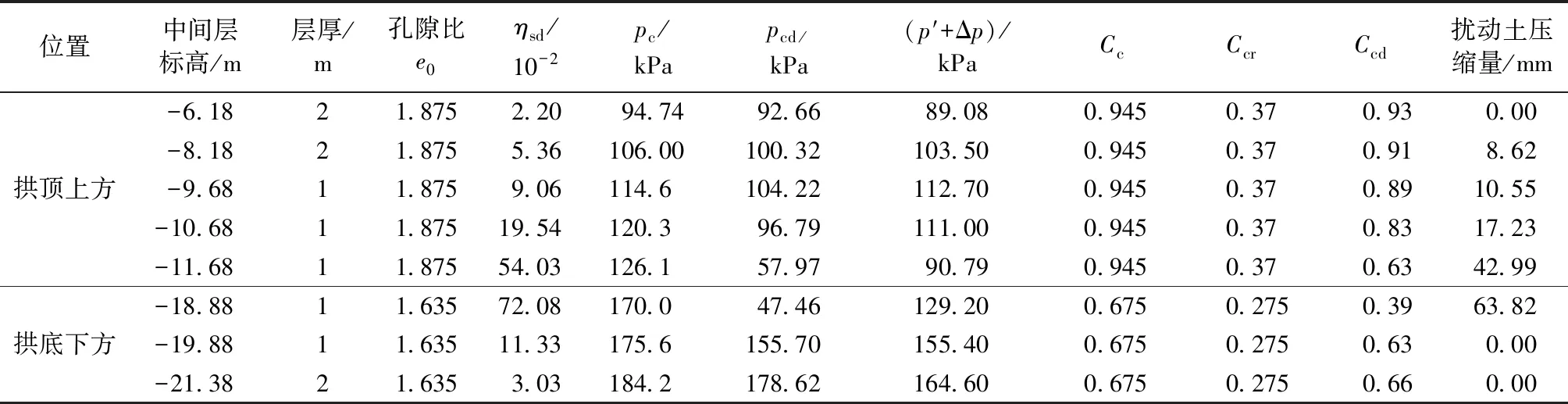
表8 沉降计算

6 结束语

依托温州市轨道交通M1线某区段的盾构隧道施工的工程背景,对温州软土进行结构性分析评价,并建立地层-盾构隧道三维弹塑性有限元模型进行施工过程数值模拟,采用数值模拟研究盾构隧道施工对地层的扰动规律以及对沉降的影响,可以得出以下结论:

1)重塑土固结试验结果与Burland所提出的固有压缩曲线基本吻合,压缩曲线可以作为评价原状土结构性的参考依据,而屈服应力比难以体现正常固结土的结构性。

2)温州原状土样的孔隙指数Iv基本位于固有压缩曲线上方,甚至位于沉积压缩曲线上方,应力灵敏度远高于天然沉积土,表明温州软土具有强烈的结构性。

3)盾构施工对土层的扰动分为三个阶段——初步发展阶段、快速发展阶段以及稳定阶段。初始发展阶段主要受开挖面支护力控制,扰动得到初步发展;快速发展阶段受卸荷作用控制,扰动范围快速扩展;稳定阶段受注浆和卸荷作用控制,扰动范围轻微扩张,扰动程度剧烈发展,而后不再发展。

4)盾构施工在周围土层引起的扰动区形状形似“眼睛”形,盾构隧道上方的扰动度分布可采用线性函数拟合,盾构隧道下方土层的扰动度分布可采用二次多项式拟合,拱腰外侧扰动度分布可采用指数函数拟合。

5)由于盾构施工的扰动作用,地表总沉降量为143.21 mm,管片下沉量为49.82 mm,均远高于地铁运行要求的标准,不考虑扰动的工后沉降计算往往偏危险。扰动沉降主要来源于盾构隧道轮廓线周围的土体,因此有必要对周围土层进行加固来控制扰动沉降。