余交换post-Hopf代数上的post-Hopf 模的Maschke型定理
王忠伟,王 勇
(1.金陵科技学院理学院,江苏 南京 211169;2.南京晓庄学院信息工程学院,江苏 南京 211171)
post-Hopf代数[1]是指带有从H⊗H到H的余代数同态,并且满足某些相容性质的Hopf代数H。post-Hopf代数与许多研究领域有着密切联系。文献[1]证明了由post-Hopf代数H的所有素元构成的集合
PH={x∈H|Δ(x)=1H⊗x+x⊗1H}
是post-Lie代数(Lie代数结构定义为[x,y]=xy-yx,∀x,y∈PH),余交换post-Hopf代数与余交换Hopf-brace是一一对应的,建立了余交换post-Hopf代数范畴与关于余交换模双代数的相关Rota-Baxter算子范畴之间的伴随函子;文献[2-3]证明了post-Lie代数的泛包络代数是post-Hopf代数;文献[4]构造了Magma代数的张量代数上的post-Hopf代数结构;文献[5]证明了post-群的群代数是post-Hopf代数,由post-Hopf代数的所有群像元所构成的集合是post-群;等等。
由此可见,作为一个刚被引入不久的概念,post-Hopf代数具有较高的研究价值和较广阔的研究前景。在此背景下,本文将post-Hopf代数的概念作进一步推广,引入了post-Hopf代数上的post-Hopf模的概念,给出了余交换post-Hopf代数上的post-Hopf模的Maschke型定理。
本文的结构如下:第一部分描述post-Hopf代数的相关概念,并引入其上的post-Hopf模的概念;第二部分描述本文的主要结果,即余交换post-Hopf代数上的post-Hopf模的Maschke型定理;第三部分为结语。
除特别说明外,本文中所有的线性空间、张量积和同态均定义在域k上。对线性空间W,V,记τW,V:W⊗V→V⊗W为平凡的扭曲映射。对余代数和余模,采用Sweedler记法:对余代数C,记余乘法Δ(c)=∑c1⊗c2,∀c∈C;对右C-余模M,记余模结构映射ρM(m)=∑m(0)⊗m(1),∀m∈M。对于未经解释的定义和记法,可参考文献[6-7]。
1 预备知识
定义1设H是Hopf代数,▷H:H⊗H→H是余代数同态,如果满足如下条件:对任意的x,y,z∈H,
x▷H(yz)=∑(x1▷Hy)(x2▷Hz)
(1)
x▷H(y▷Hz)=∑(x1(x2▷Hy))▷Hz
(2)
且左乘法
α▷H:H→End(H),α▷H(x)(y)=x▷Hy, ∀x,y∈H
在Hom(H,End(H))中是卷积可逆的,即存在唯一的β▷H:H→End(H),使得
∑α▷H(x1)∘β▷H(x2)=∑β▷H(x1)∘α▷H(x2)=ε(x)idH, ∀x∈H,
则称配对(H,▷H)为post-Hopf代数。
接下来,引入post-Hopf 代数上的post-Hopf 模的概念。
定义2设(H,▷H)为post-Hopf代数,M是H-Hopf模。如果存在线性映射▷M:H⊗M→M满足如下条件:对任意的x,y∈H,m∈M
ρ(x▷Mm)=∑x1▷Mm(0)⊗x2▷Hm(1)
(3)
x▷M(y·m)=∑(x1▷Hy)·(x2▷Mm)
(4)
x▷M(y▷Mm)=∑(x1(x2▷Hy))▷Mm
(5)
且左作用
α▷M:H→End(M),α▷M(x)(m)=x▷Mm, ∀x∈H,m∈M
在Hom(H,End(M))中是卷积可逆的,即存在唯一的β▷M:H→End(M),使得
∑α▷M(x1)∘β▷M(x2)=∑β▷M(x1)∘α▷M(x2)=ε(x)idM, ∀x∈H,
则称配对(M,▷M)为(H,▷H)-post-Hopf模。
设(H,▷H)为post-Hopf代数,(M,▷M),(N,▷N)是(H,▷H)-post-Hopf模。若线性映射φ:M→N满足
φ(x▷Mm)=x▷Nφ(m), ∀x∈H,m∈M,
则称φ是post-线性的。
进一步的,若post-线性映射φ也是H-Hopf模同态,则称φ为从(M,▷M)到(N,▷N)的(H,▷H)-post-Hopf模同态。
2 主要结果
设H是Hopf代数,M是H-Hopf模,记
McoH={m∈M|ρM(m)=m⊗1H}
为M的H-余不变子空间。
引理1设(H,▷H)是余可换的post-Hopf代数,(M,▷M)是(H,▷H)-post-Hopf模,则(McoH,▷McoHε⊗idMcoH)是平凡的(H,▷H)-post-Hopf模,即其Hopf模结构定义为
x·m=ε(x)m,ρMcoHρM|McoH, ∀x∈H,m∈McoH
证明:一方面,易知McoH是H-Hopf模且式(3)~式(5)成立。另一方面,
α▷McoH:H→End(McoH),α▷McoH(h)(m)=ε(h)m, ∀h∈H,m∈M
卷积幂等,故(McoH,▷McoH·ε⊗idMcoH)是(H,▷H)-post-Hopf模。
证毕。
引理2设(H,▷H)是余可换的post-Hopf代数,(M,▷M)是(H,▷H)-post-Hopf模,则(H⊗M,▷H⊗M)也是(H,▷H)-post-Hopf模,其中H-Hopf模结构为:
x·(y⊗m)=∑x1y⊗x2·m
ρH⊗M(x⊗m)=∑(x1⊗m)⊗x2
左作用▷H⊗M:H⊗(H⊗M)→H⊗M定义为:
▷H⊗M(x⊗(y⊗m))=∑x1▷Hy⊗x2▷Mm, ∀x,y∈H,m∈M
证明:首先,易证H⊗M是H-Hopf模。
其次,对任意x,y∈H,m∈M,由于H是余可换的,且▷H:H⊗H→H是余代数同态,所以有
ρH⊗M(x▷H⊗M(y⊗m))=∑ρH⊗M(x1▷Hy⊗x2▷Mm)
=∑x1▷H⊗M(y1⊗m)⊗x2▷Hy2
=∑x1▷H⊗M(y⊗m)(0)⊗x2▷H(y⊗m)(1)
x▷H⊗M(y·(z⊗m))=∑x▷H⊗M(y1z⊗y2·m)
=∑x1▷H(y1z)⊗x2▷M(y2·m)
=∑(x1▷Hy)⊗(x2▷M⊗H(z⊗m))
x▷M(y▷H⊗M(z⊗m))=∑x▷M(y1▷Hz⊗y2▷Mm)
=∑x1▷H(y1▷Hz)⊗x2▷M(y2▷Mm)
=∑(x1(x2▷Hy))▷H⊗M(z⊗m)
最后,由于α▷H⊗M(x)=∑α▷H(x1)⊗α▷M(x2),所以左作用▷H⊗M是卷积可逆的。因此(H⊗M,▷H⊗M)是(H,▷H)-post-Hopf模。
证毕。
设H是余可换的Hopf代数,M是H-Hopf模。对任意m∈M,定义
PM:M→M,PM(m)=∑S(m(1))·m(0)
则易知Im(PM)⊆McoH。
命题1设(H,▷H)是余可换的post-Hopf代数,(M,▷M)是(H,▷H)-post-Hopf模,则线性映射
λM:H⊗M→M,λM(x⊗m)=x·PM(m), ∀x,y∈H,m∈M
是满射的(H,▷H)-post-Hopf模同态。
证明:首先,由于H是余可换的,则易证
λM∘τM,H∘ρM=idM
从而λM是满射。
其次,对任意x,y∈H,m∈M,一方面,
λM(x·(y⊗m))=∑λM(x1y⊗x2·m)=∑x1yS(x2m(1))x3·m(0)
=∑x1yS(m(1))S(x2)x3·m(0)=∑xyS(m(1))·m(0)=x·λM(y⊗m)
故,λM是左H-模同态。另一方面,由Im(PM)⊆McoH得
ρM(λ(x⊗m))=ρM(x·PM(m))=∑x1·PM(m)⊗x2=∑λ(x1⊗m)⊗x2
故,λM是右H-余模同态,从而λM是H-Hopf模同态。
最后,对任意x,y∈H,m∈M,由文献[1]的引理2.3得
λM(x▷H⊗M(y⊗m))=∑λM(x1▷Hy⊗x2▷Mm)
=∑(x1▷Hy)S(x2▷Hm(1))·(x3▷Mm(0))
=∑(x1▷Hy)(x2▷HS(m(1)))·(x3▷Mm(0))
=x▷MλM(g⊗m)
从而λM是post-线性的。因此λM是满射的(H,▷H)-post-Hopf模同态。
证毕。
由命题1容易得到以下推论。
推论1设(H,▷H)是余可换的post-Hopf代数,(M,▷M)是(H,▷H)-post-Hopf模,则正合列
作为(H,▷H)-post-Hopf模是可裂的。
引理3设(H,▷H)是余可换的post-Hopf代数,(M,▷M),(N,▷N)是(H,▷H)-post-Hopf模,φ:N→M是线性映射。令
即
则下列结论成立:
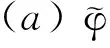
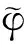
证明:(a) 显然成立。
(b) 对任意x∈H,n∈N,因为φ是左H-模同态,所以有
=∑x1n(1)S(x2φ(n(0))(1))x3·φ(n(0))(0)=∑x1n(1)S(φ(n(0))(1))S(x2)x3·φ(n(0))(0)

另一方面,因为φ是post-线性的,所以有
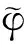
证毕。
以下,给出本文的主要结果,即余交换post-Hopf代数上的post-Hopf模的Maschke型定理。
定理1设(H,▷H)是余可换的post-Hopf代数,若post-Hopf模短正合列
作为左H-模是可裂的,且ψ,φ是post-线性的,则该正合列作为post-Hopf模也是可裂的。

故,ψ:M→N是可裂的post-Hopf模同态,从而正合列作为post-Hopf模是可裂的。
证毕。
3 结 语
Post-Hopf代数的引入进一步拓宽了Hopf代数理论的研究内容,因其与Yang-Baxter方程、Lie代数和Hopf-brace等联系紧密,所以越来越引起数学家的兴趣和关注。本文旨在进一步研究post-Hopf代数上的作用和余作用,引入了其上的post-Hopf模的概念,并给出了余交换post-Hopf代数上的post-Hopf模的Maschke型定理。

