基于自注意力机制的FCM++及其在学生评价中的应用
游 坤,朱皖宁
(金陵科技学院软件工程学院,江苏 南京 211169)
做好学生评价工作是促进教育发展的关键问题之一[1]。大多数高校目前采用“以考代评”的方式检验学生的学习成果[2],但是该方式往往形式单一、内容陈旧,难以全面评价学生的真实能力。已有很多学者对学生评价问题做出了研究,厉丹等[3]提出了一种基于hopfield神经网络的学生评价模型,相比于传统的评价方法,该方法能够更客观地评价学生的综合能力,但是模型分析的学生数量相对较少,分析指标也相对较少,在学生评价问题中的普适性较弱;陈正宇等[4]提出了工程教育认证下的人才培养与评价方法,从多方面阐述了应用型卓越工程技术人才培养应遵循的基本原则,但该方法更针对应用型高校,具有一定的局限性。聚类是一种无监督学习算法,它通过将数据集中相似的数据点划分到同一类别中,形成有意义的簇,从而帮助理解数据集中的潜在结构和模式;评价则是对对象进行质量评估的过程。将聚类应用于评价问题,可以根据聚类结果来评估对象的质量,例如学校的好坏、产品的质量等。模糊C均值聚类(fuzzy C-means,FCM)是一种基于模糊集理论的聚类算法,通过对数据进行隶属度划分,能够很好地应对数据的复杂性和噪声,在评价问题时往往比其他聚类方法更加客观和有效。但是传统模糊C均值聚类算法的初始聚类中心随机,易陷入局部最优,很多学者对此做出了改进。Stetco等[5]提出了FCM++算法,依据距离来计算数据点作为聚类中心的概率,但是其初始聚类中心仍是随机选择的。Chovancova等[6]提出了基于粒子群的模糊C均值聚类算法,根据粒子群算法决定初始聚类中心。武超飞等[7]提出了基于遗传模拟退火算法的FCM,通过遗传模拟退火算法提高模糊C均值聚类的全局聚类能力,在一定程度上避免了局部最优。但是,以上算法在学生评价问题上都没有解决同一聚类中心内数据点相似度不高的问题,不能体现学生真实水平。
为解决上述问题,本文提出了一种基于自注意力机制的模糊C均值聚类算法,旨在通过自注意力模型(self-attention)计算FCM++的初始聚类中心,再通过模糊聚类的目标函数对聚类中心和隶属度进行迭代,避免了模糊聚类存在的因初始聚类中心和隶属度随机导致的局部最优解问题,增强了评价的准确性和客观性,可以更好地体现评价对象的好坏程度。
1 储备知识
FCM是由Dunn等[8]提出、Bezdek等[9]改进发展而来的一种聚类算法。它应用模糊理论的思想,将数据划分为不同的聚类中心,与传统“硬聚类”思想不同,FCM中的数据点对于每个聚类中心的隶属度为uij,uij可被看作是数据点i属于聚类中心j的程度。根据目标函数,可以对聚类中心和隶属度矩阵反复迭代,最终根据隶属度的值决定数据点所属的类别。
FCM的算法流程如图1所示。

图1 FCM算法流程
自注意力模型是由Vaswani等[10]提出的一种模型,通过Wq、Wk、Wv等权重的迭代计算出矩阵Q、K、V,进而计算出数据点对于其他数据点的注意力。自注意力模型的算法步骤如图2所示。
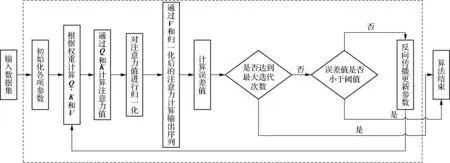
图2 自注意力模型算法流程
2 相关概念
2.1 输入矩阵
定义矩阵空间Md×n为所有d×n型矩阵构成的集合,其中d∈N*,表示单个样本输入的特征数量,n∈N*,表示样本总数。输入矩阵X满足X∈Md×n,xik表示输入矩阵X中第i行、第k列的元素,xik∈R。根据以往对学生评价的指标,本文输入矩阵中的特征选取学生学习产生的部分数据并进行归一化处理,包括课程作业完成总次数、课程作业平均成绩、课程考试平均成绩、平均考勤次数、道德品质评分、创新能力、实际能力以及运动健康等指标。
2.2 隶属度矩阵
隶属度矩阵是FCM中用于衡量数据点属于聚类中心程度的矩阵。定义矩阵空间Mn×c为所有n×c型矩阵构成的集合,其中c∈N*,表示聚类中心的总数。隶属度矩阵U满足U∈Mn×c,uij表示隶属度矩阵U中第i行、第j列的元素,uij∈R,即第i个数据点属于第j个聚类中心的程度。对于第i个数据点,其对所有聚类中心的隶属度之和为1,即
(1)
2.3 聚类中心矩阵
定义矩阵空间Md×c为所有d×c型矩阵构成的集合,表示聚类中心的总数。聚类中心矩阵V满足V∈Md×c,vj表示V中的第j个向量,即第j个聚类中心的位置。
2.4 目标函数
FCM的目标函数如下:
(2)
式中,t为隶属度因子,vj表示第j个聚类中心,U表示隶属度矩阵,V表示聚类中心矩阵。
根据FCM的目标函数,隶属度矩阵的迭代公式为
(3)
聚类中心的迭代公式为
(4)
2.5 自注意力模型
自注意力模型是通过Wq、Wk、Wv等参数计算Q、K、V,从而计算数据对于其他数据注意力的一种模型。Wq、Wk、Wv等参数通过反向传播进行更新。在处理学生评价问题中,本文使用自注意力模型将输入数据作为序列生成输出序列,再通过一个全连接层将输出序列映射为一个拥有全局信息的数据点,将该数据点作为输入数据的初始聚类中心,结构如图3所示。
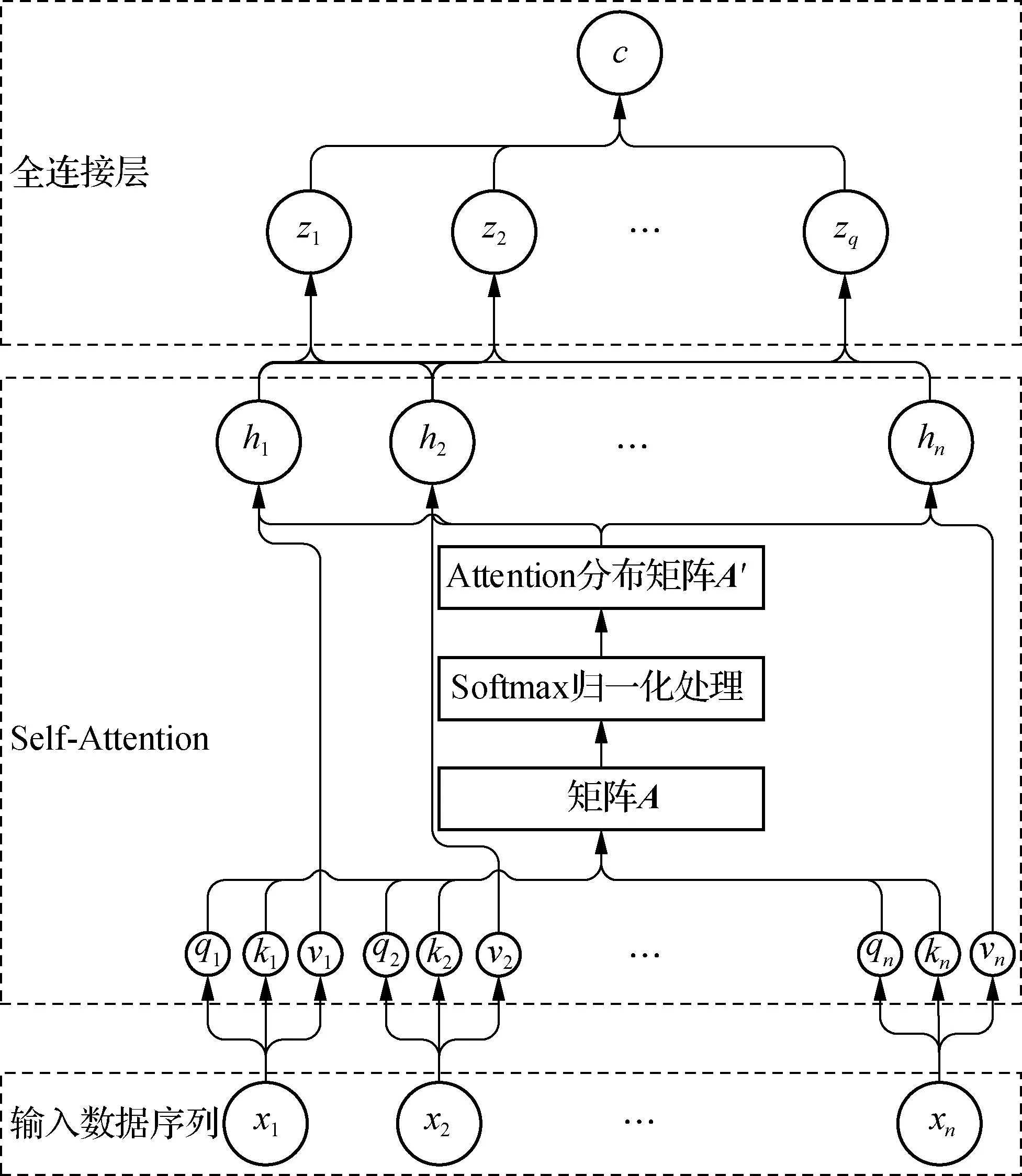
图3 学生评价问题中自注意力机制计算初始聚类中心的结构
3 基于自注意力机制的FCM++算法
定义函数
fQ_calculate(X,WQ)=WQX
(5)
fK_calculate(X,WK)=WKX
(6)
fV_calculate(X,WV)=WVX
(7)
分别用于计算矩阵Q、K和V。
定义函数
fA_calculate(Q,K)=KTQ
(8)
用于计算未归一化的注意力分布矩阵A。
定义函数
(9)
用于对注意力分布矩阵进行归一化处理得到A′。
定义函数
fH_calculate(V,A′)=VA′
(10)
用于计算全连接层的输入矩阵H。
定义函数fforward用于前向传播,函数fback用于反向传播。
定义函数fD_calculate用于计算数据点与聚类中心的距离组成的矩阵D。
定义函数
(11)
用于计算数据点作为聚类中心的概率。
定义函数
(12)
用于计算FCM目标函数的值。
定义函数
(13)
用于对隶属度矩阵U进行迭代更新。
定义函数
(14)
用于对聚类中心矩阵V进行迭代更新。
基于自注意力机制的FCM++算法具体流程如下所示。

算法1基于自注意力机制的FCM++算法

输入:输入矩阵X、训练集和测试集
输出:学校对聚类中心的隶属度矩阵,以及聚类中心矩阵
Step1:初始化当前迭代次数iteration、最大迭代次数iteration_max、自注意力层权重WQ、WK和WV,全连接层权重W和M,偏置B和F,阈值ε,聚类最大迭代次数iteration_fcm_max,聚类当前迭代次数iteration_fcm等参数
Step2:计算函数fQ_calculate,fK_calculate和fV_calculate,得到矩阵Q,K和V
Step3:计算函数fA_calculate,得到未归一化的注意力分布矩阵A
Step4:计算函数fsoftmax,得到归一化后的注意力分布矩阵A′
Step5:计算函数fH_calculate,得到全连接层的输入矩阵H
Step6:计算函数fforward,进行前向传播,得到误差值MSE(H)
Step7:若MSE(H)<ε,或iteration=iteration_max,那么停止迭代,得到初始聚类中心c0,并将c0放入初始聚类中心集合C′中,进入Step9
Step8:计算函数fback,进行反向传播,更新参数
Step9:计算函数fD_calculate,得到数据点与初始聚类中心集合中元素的距离构成的矩阵D
Step10:根据矩阵D分别计算所有数据点属于初始聚类中心的可能性P
Step11:若当前初始聚类中心集合C′中的元素个数小于目标个数,进入Step12;否则进入Step13
Step12:根据可能性P判断该数据点是否作为聚类中心,若是,加入初始聚类中心集合C′,返回Step9;若不是,直接返回Step9
Step13:根据聚类中心,通过函数fupdate_Uij计算隶属度矩阵
Step14:根据隶属度矩阵,通过函数fupdate_Vk更新聚类中心矩阵
Step15:计算目标函数fobject并记录,如果并非第一次记录,那么与上一次记录比较,若差值小于阈值ε,或迭代次数iteration_fcm达到最大迭代次数iteration_fcm_max,迭代结束,进入Step16;否则iteration_fcm=iteration_fcm+1,并进入Step13
Step16:输出当前隶属度矩阵,以及聚类中心矩阵
算法结束

本文改进了FCM++算法,通过自注意力机制,将输入数据序列转换为具有全局特征的序列,再通过一个全连接层将其映射到初始聚类中心上。
4 实验分析
4.1 数据集
本文根据Open University Learning Analytics Dataset提供的4 307组学生数据对学生进行评价实验,将数据进行清洗后分为3个数据集Student1、Student2和Student3,3个数据集的具体情况如表1所示。

表1 数据集的数据组成情况
对上述数据集归一化后的数据进行PCA降维,结果如图4所示。

Student1
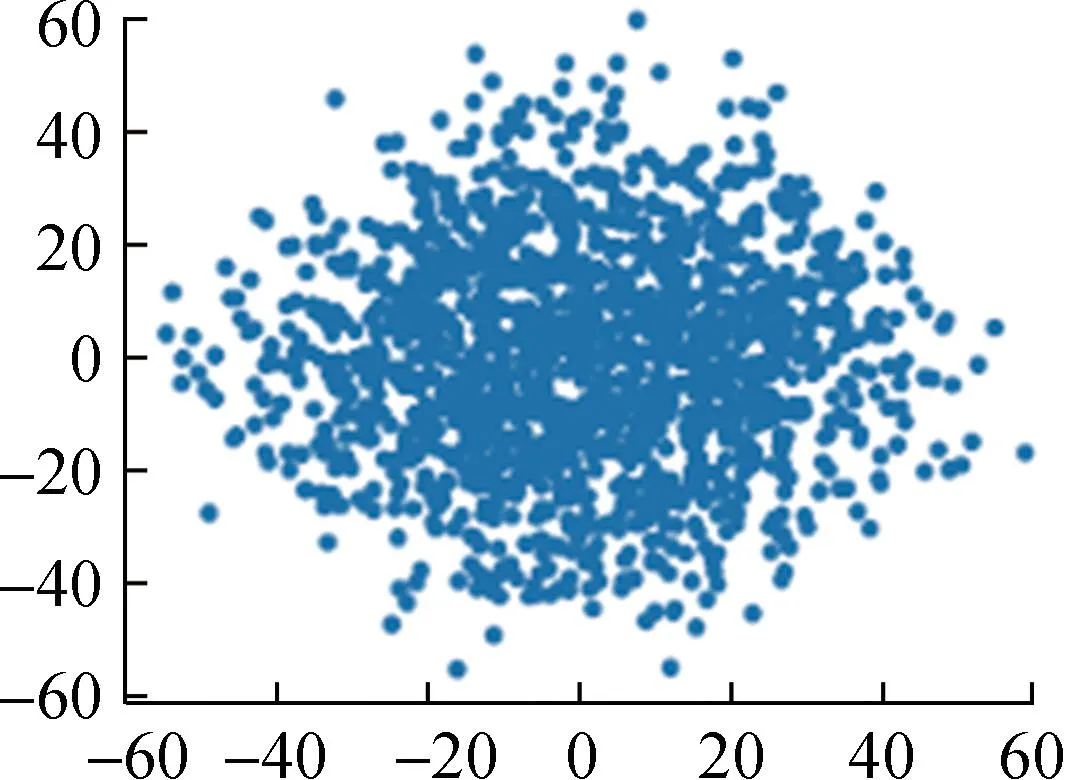
Student2
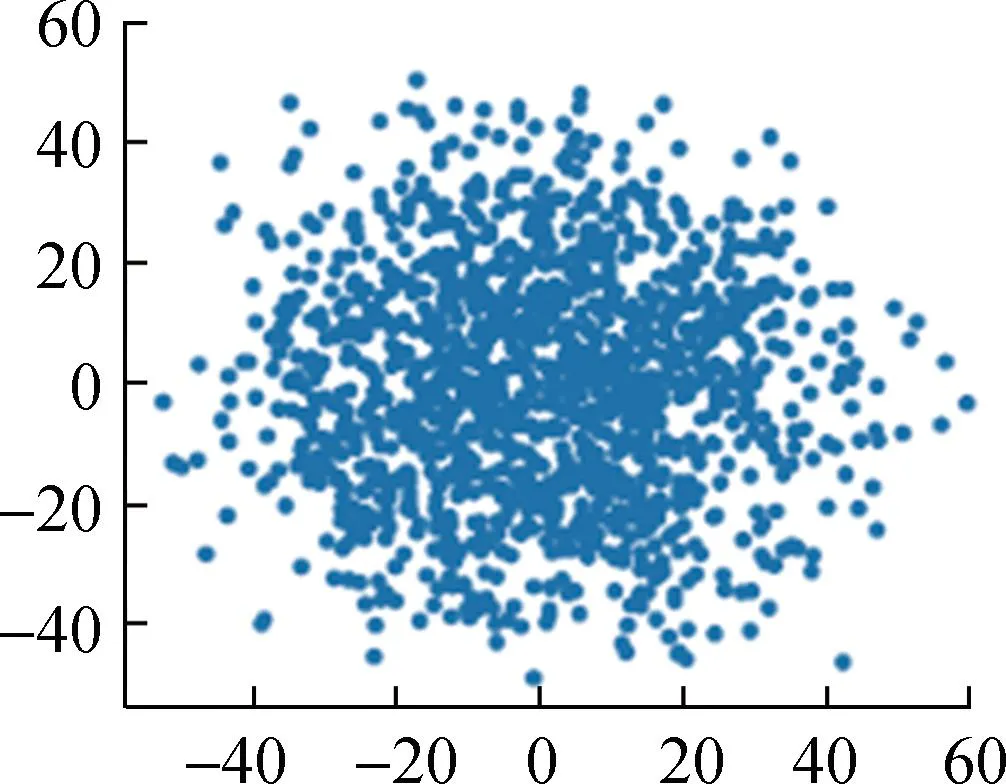
Student3
4.2 对比算法
经过调研,目前在学生评估方面,国内并没有使用模糊聚类进行评估的先例,因此为了说明本文提出的基于自注意力机制的FCM++算法在解决学生评价问题上更优,本文使用以下模糊聚类与经典聚类算法进行实验结果的对比。
1)FCM++。FCM++算法是一种改进的模糊C均值聚类算法,它的主要特点是在进行FCM聚类之前,通过特定的方法生成一个初始聚类中心。该算法可以有效地解决FCM算法对初始聚类中心选择敏感的问题。
2)基于粒子群的模糊聚类算法。基于粒子群优化的FCM聚类算法是一种改进的模糊C均值聚类算法,该算法利用粒子群优化算法的全局寻优能力,克服了FCM算法易陷入局部极小值和对初始值敏感的问题。
3)BFC。贝叶斯模糊聚类(BFC)算法是一种结合了贝叶斯理论和模糊聚类的方法,它采用最大后验概率理论处理模糊划分,进而获取最终的聚类结果。该算法有效地结合了概率论和模糊论两者的优点,能够获取全局最优解并估计聚类个数。
4)DTW-K means。DTW-K means算法是一种结合了动态时间规整(DTW)和K-means的时间序列聚类方法。该算法首先使用DTW方法计算时间序列之间的相似度,然后利用K-means算法进行聚类,能够处理时间序列的非线性对齐,使得相似的但在时间上有所偏移的序列也能被正确地归为一类。
4.3 评估指标
本文选用S_dbw、DB指数和Dunn指数作为评价聚类效果的标准。
S_dbw是一种通过衡量聚类结果的簇间密度和簇内方差来评估聚类有效性的指标,该指标越小,说明聚类越有效。由于使用该指标的验证方法在单调性、噪声、密度、子群和倾斜分布等方面都表现良好,因此本文选择其作为衡量聚类效果的指标之一[11]。S_dbw又分为Scat和Dens_bw,其中Scat用于衡量簇间密度,Dens_bw用于衡量簇内方差。
Dunn指数的计算方法是将最小的类间距离与最大的类内距离的比值作为评估标准[12]。Dunn index越大,说明类内样本越接近,类间样本越远离,聚类效果越好。
DB指数(Davies-Bouldin index)由Davies D.L.和Bouldin D.W.在1979年提出[13],它通过计算每个类簇内部的平均距离和类簇之间的距离来评估聚类效果。DB index越小,说明聚类效果越好。
4.4 实验结果
本文实验设置学习率learning_rate=0.1,神经网络最大迭代次数iteration_max=30 000,隶属度因子t=2,FCM++中参数p=2,聚类最大迭代次数iteration_fcm_max=2 000,阈值ε=0.001。本文通过实验将基于自注意力机制的FCM++算法与4.2节中的算法进行聚类效果的比较。
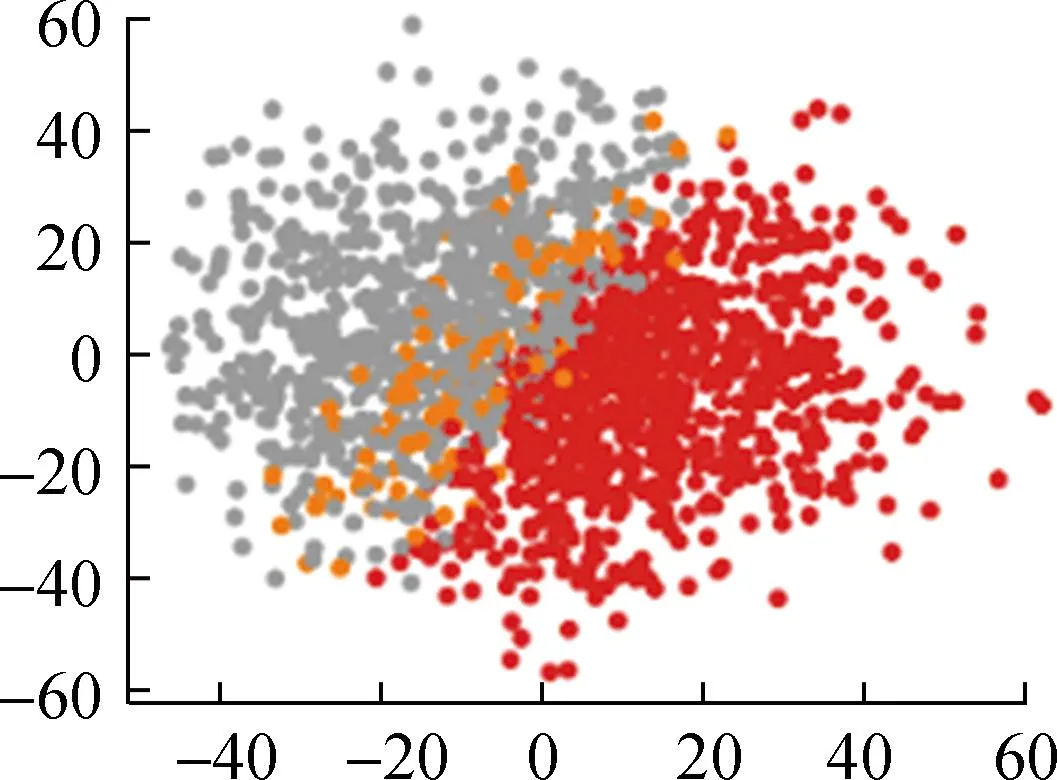
各算法所得的聚类结果如图5所示。
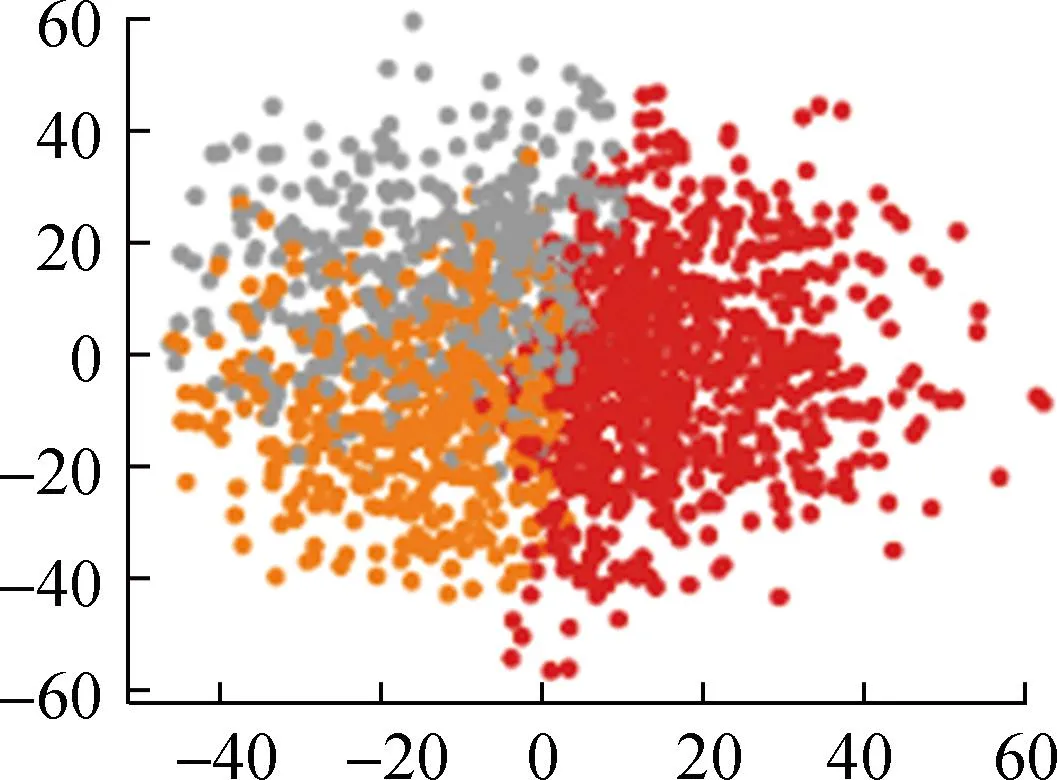
(a) 基于自注意力机制的FCM++
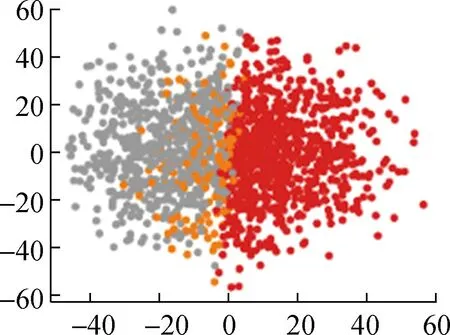
(b) 基于粒子群的模糊聚类算法
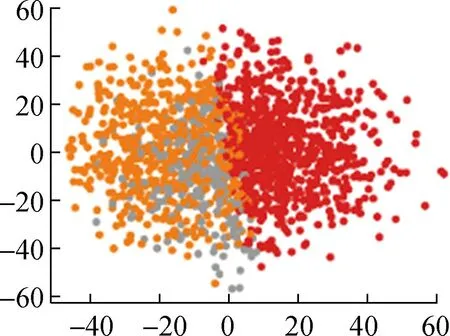
(c) FCM++
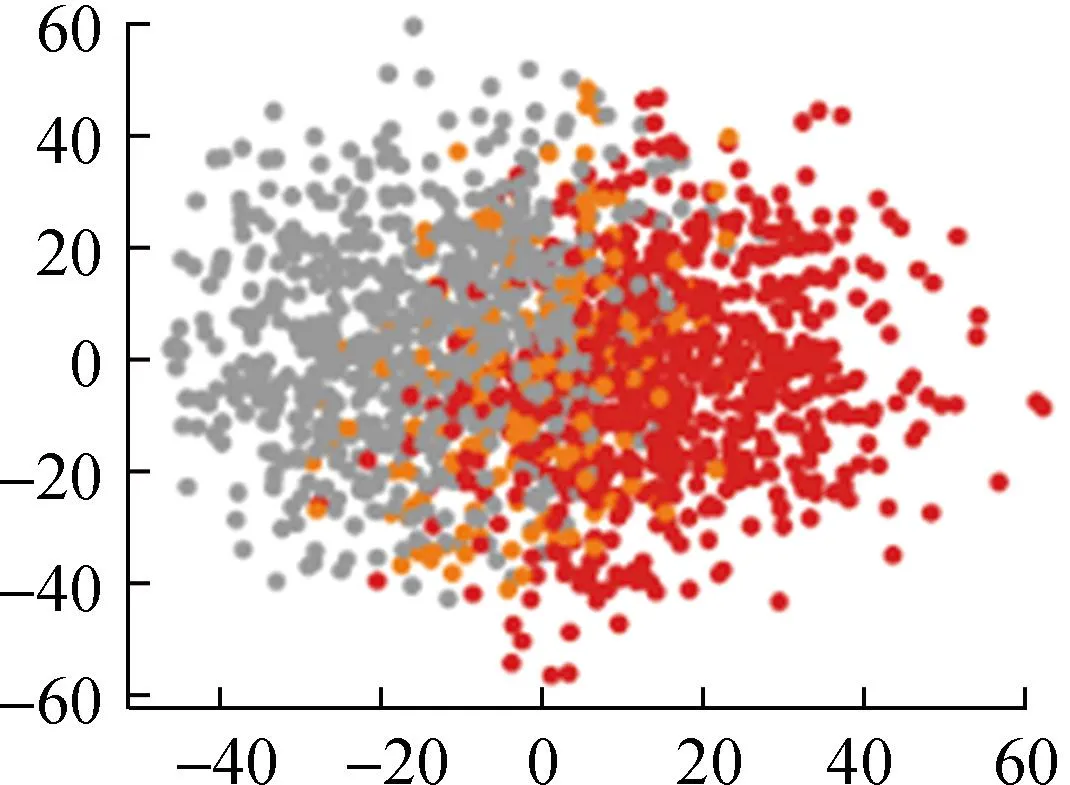
(d) BFC
(e) DTW-K means
从直观角度来看,本文提出的基于自注意力机制的FCM++算法聚类结果明显优于FCM++算法、基于粒子群的模糊聚类算法以及BFC和DTW-K means算法。这是因为多头自注意力层能够捕捉输入数据的全局依赖关系,经过全连接层映射为一个初始聚类中心,传统的模糊聚类算法存在聚类随机性强、无法反映数据内部特征的问题。下面本文将根据聚类指标对上述5种算法的聚类结果进行计算和对比,具体结果如表2所示。

表2 各算法评估指标结果
可以看出,本文提出的基于自注意力机制的FCM++算法在簇间密度和簇内方差上优于其他模糊聚类算法和经典聚类算法。相比于基于粒子群的模糊C均值聚类算法,本文算法的DB指数降低了19%,Dunn指数提高了26%。在学生评价问题中,本文算法可以更准确、更客观地对学生数据进行聚类,从而评估学生的能力。但是,基于自注意力机制的FCM++存在训练时间长、迭代次数多等问题,在面对大量数据时耗时偏长。由于学生评价问题中数据集相对偏少,因此基于自注意力机制的FCM++算法表现更优。
5 结 语
本文提出了一种基于自注意力机制的FCM++算法,在FCM++的基础上改进了其初始聚类中心的选取,通过自注意力机制将输入的数据映射到具有全局信息的数据中,再将这些数据通过一个全连接层映射到初始聚类中心,提高了聚类的簇间密度和簇内方差,增强了评价的准确性和客观性。但是,该算法在面对庞大数据集时往往会产生训练时间过长等问题,如何在缩短训练时间的基础上进一步增强评价的准确性是未来进一步研究的方向。

