线性长波越过水下环礁引起的Bragg共振分析

傅丹娟，刘必劲，毛豪东，张振伟

（1. 厦门理工学院土木工程与建筑学院 ，福建 厦门 361024；2. 浙江大学海南研究院，海南 三亚 572025）

波浪Bragg 共振指在特定频率波的传播方向上与某些特殊地形（如正弦沙纹、系列人工沙坝）相互作用，而使波产生最强反射的现象。波浪Bragg 共振最早由Davies［1］提出，他在研究波浪作用于水下有限正弦沙坝地形时发现，当入射波波长为沙坝波长2倍时，共振产生且反射系数最大。之后学者们也进行相关实验验证此结论［2-4］。受此启发，科学家们提出建设系列周期性人工沙坝或潜堤来抵抗波浪侵袭的设想，以达到生态建设及海岸防护协调发展。近年来，关于海底周期起伏地形激发的波浪Bragg 共振的物理机制及应用研究已成为水波研究的一个热点［5-12］。且随着越来越多的工程项目在岛礁上开发和建设，波浪在岛礁上的传播变形也越来越受到学者们的关注。然而，岛礁与常见的缓变岸滩 （沙坝、潜堤、陆架等）相比，岛焦波浪的传播变形规律有较大的不同。珊瑚环礁是岛礁极具代表性的形式之一，发育成熟的珊瑚环礁中心一般有宽广的深浅不一的泻湖。如环礁这般高低起伏的地形，是否具备激发波浪Bragg 共振的特性，还未见系统研究。为此，本文基于线性长波方程给出波浪越过水下环礁传播变形的解析解，并定义波浪散射系数，探讨环礁地形周围Bragg 共振的存在性及存在条件。

1 模型及解决技术

1.1 理论推导

环礁地形剖面如图1 所示。假设地形是轴对称的，采用极坐标系，坐标原点为环礁泻湖中心。整个区域的水深函数h（r）表示为

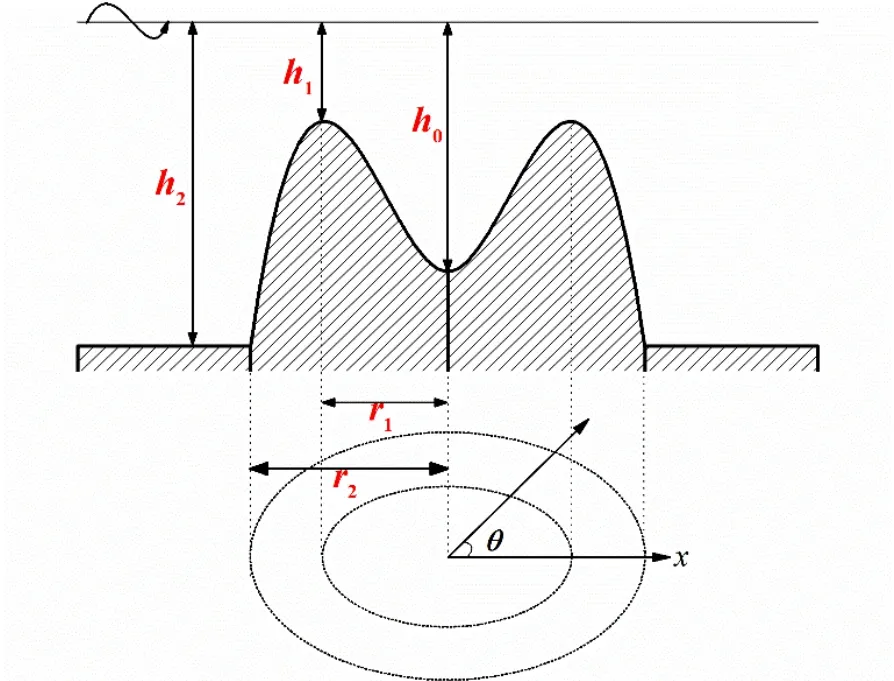
图1 环礁地形截面图：s= 2Fig.1 Section sketch of atoll: s= 2

式（1）中：r1为中心到脊顶处的横向距离；r2为中心到环礁边界的横向距离；h0为中心处水深；h1为脊顶处的水深；h2为外海水深；s 为任意正有理数。地形参数a和b由r1、h0、h1和m 决定：a = （h0-h1）/，b =。另外，r2与h2满足关系式

基于长波假设，对于轴对称地形，采用如下方程来描述波浪的运动：

式（3）中：η（r， θ） 为自由水面函数；h（r）为静水水深；ω为角频率；g 为重力加速度。

对于水深如式 （1） 所示的地形，方程（3）的解可表示为

式（4）中：

式（4）、（5）中：k2为入射波波数；Jn是第一类的n阶Bessel函数；Hn是第一类的n阶Hankel函数；εn是Jacobi符号；m、p、q为整数且满足m ≥ 1、 p ≥ 1、 q ≥ 2。

1）当m =1时，有

式（8）中：u=w/g。

2）当m = 2时，有

3）当m > 2时，有

4）当p＜q时，有

5）当q ＜p＜2q时，有

6）当p > 2q时，有

式（14）、（15）中：

基于连续性条件，在相邻区间交界处（即r=r1和r=r2）波高相等，流量相等，可得待定系数An、β1，n、β2n及Dn的值。

1.2 散射系数

定义散射系数为

由式（18）可知，KS是关于方向角θ和径向r的函数。

2 环礁激发的Bragg共振

2.1 Bragg共振存在性

为研究环礁地形上Bragg 共振的存在性，考虑如下的地形参数：h1=10 m，h0=20 m， h2= 21.5 m，r1= 1 000 m， r2= 1 200 m，S = 2r1=2 000 m， s = 4；考虑波长计算范围：0＜ 2S/L ≤ 3， 则无因次水深计算范围为：0＜ k2h2＜ 0.1，满足浅水方程适用范围。其中，S是岛礁脊顶间距。

图2给出了环礁迎浪面不同方向散射系数随波长的变化趋势。由图2可以看出，迎浪面正面（θ =π） 有Bragg 共振产生，显示在2S/L=1、2、3 附近（即：环礁脊顶距离与半波长比值的整数倍附近），散射系数达到最大值和极大值，说明在这些频率下环礁对波浪的散射最强。但是，共振频率并不落在整数上。如图2 所示，主共振在2S/L = 1.16 时产生，次共振位于2S/L=1.92 处。之前，众多学者［13-15］对水下周期性起伏地形 （如正弦沙纹、人工沙坝、系列沟槽等）激发的Bragg共振反射问题进行研究时，也发现共振发生的频率不会出现在2S/L=1 处，而是会有所偏移，如系列沟槽等地形主频出现在2S/L>1 处，而对于正弦沙纹及人工沙坝等地形，主频出现在2S/L＜1 的位置。可见，三维的环礁地形跟沙坝、沟槽等二维地形所激发的Bragg共振在频偏移上还是有差异，需进一步加以更深入的研究。

图2 不同方向散射系数随波长2S/L的变化趋势（h1 =10 m, h0 =20 m, h2 = 21.5 m, r1 = 1 000 m, r2 = 1 200 m, s = 4）Fig.2 Relation between scattering rate and 2S/L at different directions（h1 =10 m, h0 =20 m, h2 = 21.5 m, r1 = 1 000 m, r2 = 1 200 m, s = 4）

由图2可见，随着方向的的偏转，共振频率的偏移程度越大。在θ =3π/4，θ =π/2方向上，已不满足Bragg 共振的规律，主振频率大大地偏离了2S/L=1 位置。还可以观察到，当2S/L=2.24 时，θ =3π/4方向共振产生，而此时 θ = π 方向上的散射系数刚好接近极小值。

图3 给出了频率2S/L = 1.16、1.56 和2.24 时的环礁周围的整体波振幅分布。从图3 可见，当2S/L = 1.16迎浪面的散射效应非常强，观察到明显的驻波存在；当2S/L = 1.56时，迎浪面散射很小，波振幅没有明显的变化，波能量主要集中在山脊处和背浪面；当2S/L = 2.24 时，可以观察到θ =3π/4 方向上有驻波存在，而迎浪面正向（θ =π）的波幅反而更小。

图3 不同频率下的波振幅分布图Fig.3 Amplitude distribution of wave with different frequencies

2.2 环礁泻湖深度对Bragg共振的影响

由上文可知，环礁可以激发其在迎浪面正面的Bragg 共振。本节主要讨论环礁所环抱的中心泻湖深度对Bragg共振的影响。取地形参数h1=10 m，h2=21.5 m，r1=1 000 m，r2=1 200 m，泻湖深度h0分别取h0=20 m、h0=15.2 m、h0=10.038 m，对应的参数s 为4、5、16，即深度由深到浅。不同深度下，散射系数随波长2S/L的变化趋势如图4所示。

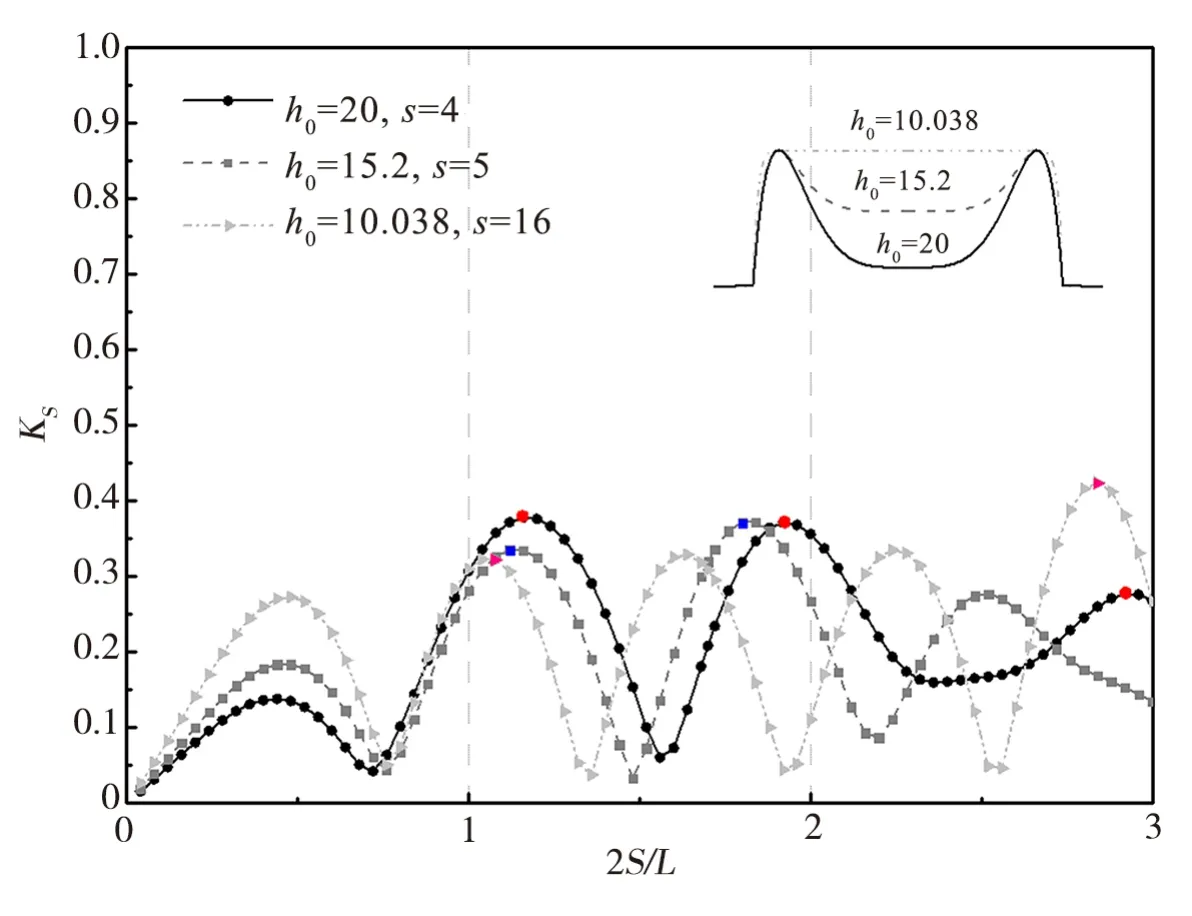
图4 不同泻湖深度，散射系数随波长2S/L的变化趋势（h1 =3.2 m, h2 =21.5 m, r1 = 1 000 m, r2 = 1 200 m）Fig.4 Relation between scattering rate and 2S/L at different lagoon depth（h1 =10 m, h0 =20 m, h2 = 21.5 m, r1 = 1 000 m, r2 = 1 200 m）

由图4可以看出，随着深度的变浅，即使是正向处的散射也越来越不满足Bragg共振规律，如h0=15.2 m，h0=10.038 m情况所示，但是在 2S/L=1附近还是可以取到散射系数的极大值。

3 结论

本文基于线性长波理论研究长波越过水下环礁激发的Bragg 共振问题。研究发现，有深泻湖的水下环礁具备产生Bragg共振的特性，当其顶部泻湖的直径约为1/2入射波长的整数倍（即2S/L=1，2S/L=2，2S/L=3）时，将激发迎浪面正面（θ =π）的水波共振，将很大的一部分波浪散射于外海。共振规律随着方位的偏移及泻湖深度的变浅而逐渐消失；在θ =3π/4，θ =π/2 方向上，已不满足Bragg 共振的规律，主振频率大大地偏离了2S/L=1 位置，且随着深度的变浅，即使是正向处的散射也越来越不满足Bragg 共振规律；在另一些特定的入射波频率下，环礁还可激发其他方位上的共振，如当入射波频率为2S/L=2.24时，可激发θ =3π/4方位上共振。

环礁激发的Bragg 共振现象的发现，将补充现有的水波Bragg 共振理论，为岛礁周围的工程建设及船舶航行提供一定的理论指导。