无监督异常检测的深度变分自编码高斯混合模型

江连吉，陈玉明*，钟才明，曾高发

（1. 厦门理工学院 计算机与信息工程学院，福建 厦门 361024；2. 宁波大学科学技术学院信息工程学院， 浙江 宁波 315212；3. 厦门市执象智能科技有限公司， 福建 厦门 361024）

无监督异常检测是机器学习中的基本问题之一［1-2］，它在许多领域都有广泛的应用，如网络安全、复杂管理系统和医疗卫生等。尤其在网络安全领域，随着互联网的飞速发展，网络流量不断增长，网络入侵、黑客攻击和恶意程序注入等现象频繁出现。据《2021 年中国互联网安全报告》，2021 年API攻击增长超200%，DDos 攻击事件同比增长约60%，Web 应用攻击高达229.83 亿次，同比增长141.3%［3］。因此，提高网络入侵检测系统的性能和准确率显得尤为关键。

早期的入侵检测主要是基于模式的硬编码规则［4-5］，但随着机器学习和深度学习的发展，异常检测开始采用有监督和无监督的机器学习模型［6-11］，如决策树模型（decision tree，DT）［12-13］、支持向量机模型（support vector machine，SVM）［14-16］和高斯混合模型（gaussian mixture model，GMM）［17-18］。由于异常数据比正常流量数据少，存在数据不平衡与难以获得有效标签的问题。为解决这些问题，有学者开始采用自编码器（autoencoder，AE）［19-21］、变分自编码器（variational auto-encoders，VAE）［22-23］和生成对抗网络（generative adversarial networks，GAN）［24-26］等模型进行检测。这些模型能对异常数据进行生成重构，解决了无法获得有效标签数据集的问题，并能应对更多未知类型的异常数据。然而，它们在重构数据样本时往往忽略了正常样本本身的内部结构和低维空间的表征。

目前，用于无监督异常检测的方法大致可以分为3类。第一类是基于重构的方法。如通过深度自编码器对样本进行重构，将重构后的样本与训练样本进行比较，通过设定阈值，把重构误差小的归为正常样本。这类方法由于只从重构误差这一方面进行异常分析，所以存有大量异常样本经过重构后仍然与正常样本接近的问题。第二类是基于聚类的方法，如K-means、CBLOF（基于聚类的局部异常因子）算法、CMGOS（基于聚类的多维高斯异常得分）算法等。这些传统技术主要通过两个步骤来进行检测，即先进行降维，然后进行聚类分析。由于这两个步骤是分开学习的，因此在降维过程中可能会丢失聚类分析的关键信息。第三类是基于单分类的方法，如利用SVM（支持向量机）对样本进行二分类。这类方法由于异常样本的数量往往少于正常样本，随着样本维度的增加会导致检测精度的下降。为更好地学习到原始样本的低维特征，同时避免自编码器自身的局部优化问题，减少重构误差，本文采用联合优化深度变分自编码器和高斯混合模型参数的方法，并利用单独的估计网络促进混合模型的参数学习，提出一种由压缩网络和估计网络组成的深度变分自编码高斯混合模型（DVAGMM）。

1 深度变分自编码高斯混合模型的建立

1.1 网络结构

DVAGMM 模型的网络结构如图1 所示。从图1 可见，该模型包含压缩网络和估计网络两个部分。压缩网络由变分自编码器组成，可以将初始输入样本X 进行降维，并计算低维空间的均值μ(X)和方差σ(X)，从而获得N(μ(X)，σ(X))的高斯分布。这个分布会被重采样得到低维表征Zl，然后再通过解码器进行解码重构，从而获得重构样本X'。在估计网络中，使用余弦相似度Z1和欧氏距离Z2来衡量原始样本X 与重构样本X'之间的差异，并将它们作为重构误差与重采样后的低维特征Zl一起作为输入Z。最后，使用高斯混合模型对每个样本进行密度估计，得到整个网络的最终输出π̂。

1.2 压缩网络

压缩网络的作用是将输入样本X进行压缩降维获得的样本进行低维表示后再进行重构，其主要由编码器和解码器组成。编码器、解码器的结构如图2、3所示。由图2可见，样本X通过编码器学习到其低维空间的后验分布P(Zl|X)～N(μ(X)，σ(X))，同时对该分布进行随机采样获得低维变量Zl。

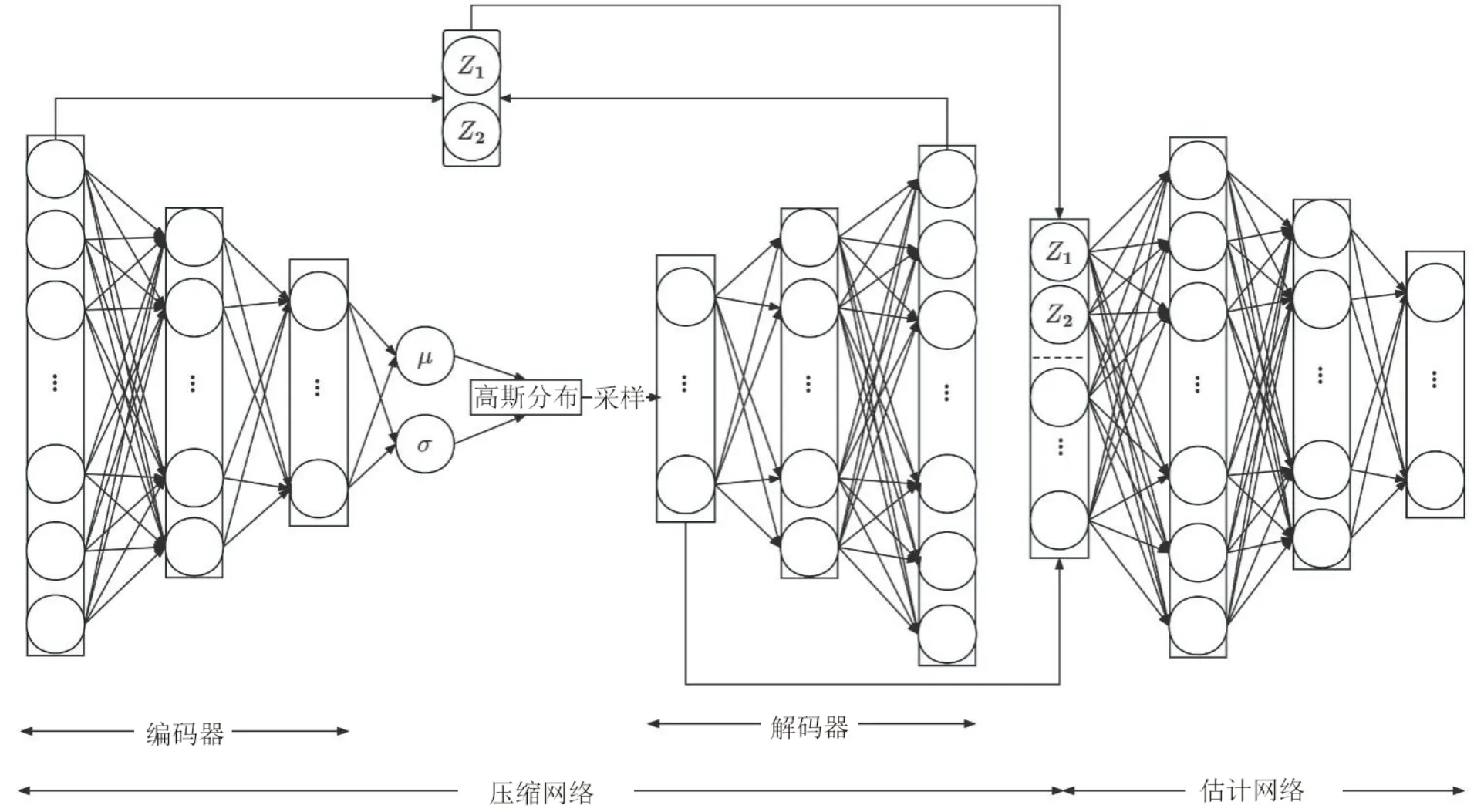
图 1 DVAGMM的网络结构Fig.1 Network structure of DVAGMM

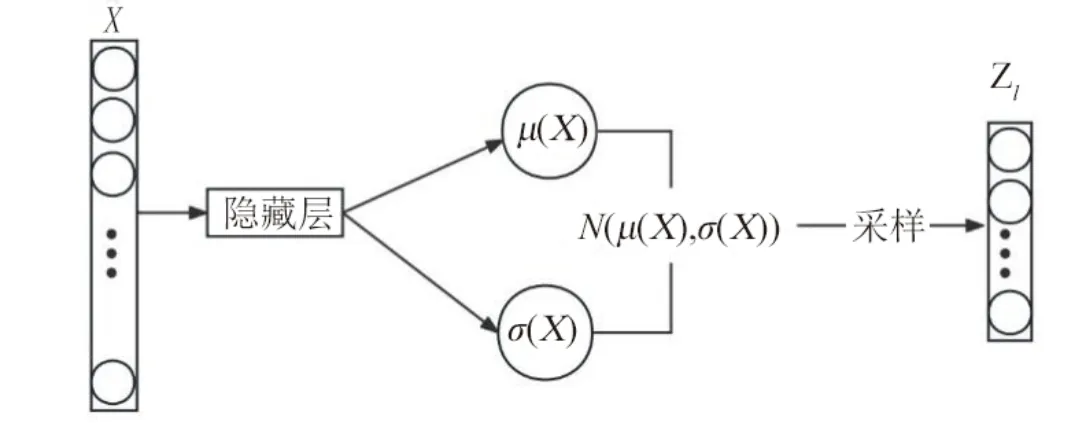
图 2 编码器的网络结构Fig.2 Network structure of the encoder

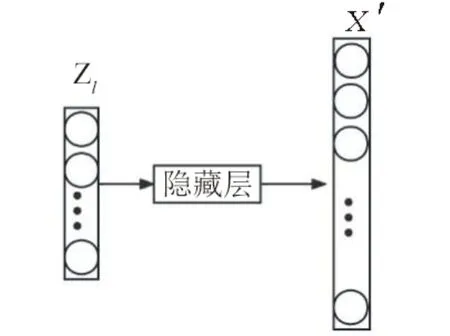
图 3 解码器的网络结构Fig.3 Network structure of the decoder

将采样得到的低维变量Zl输入到解码器中，通过隐藏层进行解码重构，最终获得重构样本X'；通过函数h( ⋅，⋅)和f( ⋅，⋅)计算重构误差，并与低维变量Zl合并成Z输出，具体表示为

式（1）～（3）中：h( ⋅，⋅)为余弦相似度函数；f( ⋅，⋅)为样本间欧式距离；Z为估计网络的输入。

1.3 估计网络

输入样本的低维表示Z，通过以高斯混合模型为基本框架的估计网络，对低维样本进行密度估计，得到估计网络的输出π̂。区别于传统的高斯混合模型，该网络在训练过程中可以直接通过计算未知混合变量的均值、协方差和该变量的分布，估计出高斯混合模型中的参数和样本的似然，而不需要通过传统的期望最大化（EM）算法对参数进行迭代估计。该估计网络的关键在于，当混合变量经过多层神经网络时，能通过计算得出样本混合成分的概率，给出低维表征Z和一个整数K作为混合成分的数量。估计网络利用多层神经网络来进行成分预测，计算公式为

式（4）～（5）中：π̂是一个K 维向量，通过归一化指数函数（softmax 函数）进行成分预测；P 是以θm为参数的MLN（多层神经网络）的输出。给定一批N个样本和它们的成分预测，∀1 ≤k ≤K，就可以进一步估计出高斯混合模型中的参数。即

这个概率分布称作样本能量，在异常检测中，其能量值越大，则被分为异常样本的概率也越大。

1.4 损失函数

DVAGMM 模型采用联合优化的方式对目标函数进行优化。为同时优化压缩网络与估计网络中的参数，提出新的联合损失函数，该函数主要分为4个部分。第一部分主要由样本能量构成；第二部分为KL 散度；第三部分为压缩网络中变分自编码器产生的重构误差的损失；第四部分为正则项，用于防止矩阵出现不可逆的情况。第一部分可以表示为

式（10）中：N 表示样本个数；λ1为平衡系数；E(zi)表示第i个样本的样本能量。通过最小化样本能量可以找到压缩网络与估计网络的最优组合。第二部分损失的目标是使所有样本的边际与p(x)最大化，计算公式为

式（11）中：p(XZl)为 X 和Zl的联合先验分布；p(Zl|X)为隐变量Zl的真实条件分布。两边取对数再积分，可得

式（12）～（13）中：GKL( ⋅∥⋅)为KL 散度。因为GKL( ⋅∥⋅) ≥0，所以的变分下界，记为GELBO（evidence lower bound，ELBO）。该网络的优化目标可以简化为最大化GELBO，GELBO由KL 散度和重构误差组成。其中，KL 散度表示隐变量Zl的真实分布p(Zl|X)与近似后验分布q(Zl|X)之间的差异，KL 散度越小，两个分布越相似。重构误差指重构样本与原始样本之间的差异，用样本的欧氏距离或余弦相似度表示。

假设隐变量Zlw的真实分布p(Zl，w)服从均值为0，方差为1的标准正态分布，可以得到：

因此，第二部分的损失为

第三部分的损失为重构误差，计算公式为

第四部分的损失为正则化项，用于防止矩阵出现不可逆的情况，其具体公式为

综上，联合损失函数L可表示为

式（18）中：λ1、λ2为用于平衡以上4项的参数；L(Xi，X'i)为重构损失函数。

2 实验结果与分析

2.1 数据集

公共基准数据集的统计数据如表1所示。

表 1 公共基准数据集的统计数据Table 1 Statistics for public benchmark datasets

表1 中，KDDCUP 数据集来自于1998 年的DARPA（美国国防高级研究计划局）入侵检测评估项目，是网络入侵检测的基准数据集。本次实验选取数据集总数的10%，实验样本个数为494 021 个，包含了41 个维度，其中34 个是连续型特征，7 个是离散型特征。对于离散特征，使用One-hot 编码。最终得到一个120 维度的数据集。由于20%的数据样本被标记为“正常”，其余的被标记为“异常”，“正常”样本属于少数群，因此，在这个任务中，“正常”的样本是被看作异常来进行处理的。

Thyroid（甲状腺）数据集从ODDS（original owners of database）数据库中获得。原始数据集中一共有3 772个样本6个特征维度，总共有3个类。在这个任务中，因为功能亢进类是个明显的少数类，所以功能亢进类被视为异常类，其他两个类被视为正常类。

Arrhythmia（心律失常）数据集也从ODDS 数据库中获得。稀少的类，包括3、4、5、7、8、9、14和15，被组合成异常类，其余的类被合并为正常类。

KDDCUP-Rev 数据集来自KDDCUP。保留所有标记为“正常”的数据样本，并随机抽取标记为“异常”的样本，使“正常”和“异常”之间的比例为4∶1，这样就得到1 个异常比例为0.2 的数据集。其中“异常”样本属于少数群体。需要注意的是，“异常”样本不是固定的，每一次运行都将从KDDCUP中随机抽取“异常”样本。

2.2 网络参数设置

DVAGMM 模型的压缩网络参数如表2所示。表2中，FC表示全连接层；Sampling表示对数据进行重采样，将低维数据映射到N(Zmean，e0.5Zvarε)的高斯分布后对该分布进行采样，最终得到原样本的低维表示Zl。其中，Zmean、Zvar分别是Zl的均值和方差，ε是服从N(0，1)的随机数。

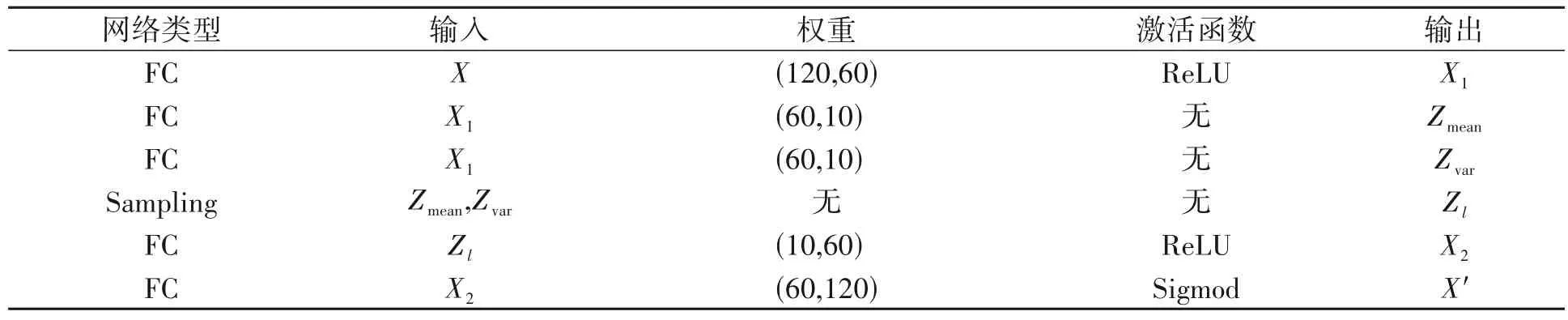
表 2 压缩网络参数Table 2 Compressed network parameters

DVAGMM模型的压缩网络参数如表3所示。

表 3 估计网络参数Table 3 Estimated network parameters

表3中，Z1、Z2表示压缩网络产生的重构误差。这里采用欧式距离和余弦相似度作为度量，计算公式分别为

为防止模型产生过拟合的现象，在估计网络的第二层设置Dropout 层。权重0.5 表示在前向传播的过程中让某个神经元的激活值以50%的概率停止工作，以增强模型的泛化性能，使其不过于依赖局部特征。最后，通过softmax函数激活后输出最终结果π̂作为样本在低维空间的密度估计。

其余超参数的设置如训练次数epochs = 200，每次的批量大小batch_size = 1 024。在模型优化方面，训练采用Adam 优化器，其中的超参数设置如学习率learning_rate = 1 × 10-4，平衡系数λ1= 0.1，平衡系数λ2= 0.005。

2.3 实验结果

本次实验采用平均精度、召回率、F1指标对异常检测性能进行度量。根据表1数据集中的异常比率，实验通过设置阈值来对异常样本进行判别。例如在KDDCUP 数据集上，设置密度估计值前20%的数据样本标记为异常样本，并把异常样本归为正例，正常样本定义为负例。相应地，定义精确率P、召回率R和F1指标如下：

式（21）～（23）中：TP 为真正例，指的是将异常样本正确分类为异常样本；FP 为假正例，指的是将正常样本错误分类为正常样本；FN为假负例，指的是将异常样本错误预测为正常样本。

将DVAGMM 与OC-SVM、DCN、DSEBM、PAE 这几个流行的异常检测算法进行比较。OC-SVM（one-class support vector machine）是一种基于核函数的支持向量机，本实验采用的是RBF（radial basis function）核函数［27］。DCN（deep clustering network）深度聚类网络是一种最先进的通过k-means调节自动编码器性能的聚类算法［28］，将这项技术应用于异常检测任务，是将样本与其聚类中心之间的距离作为异常检测的度量标准（样本距离其聚类中心较远的被视为异常样本）。DSEBM（deep structured energy based model）基于深度结构化能量的模型是一种用于无监督异常检测的深度学习方法［29］。在DSEBM-e 中，样本能量被用作检测异常的度量标准。DSEBM-e 和DSEBM-r共享相同的核心技术，但是DSEBM-r使用重建误差作为异常检测的度量标准。PAE是将DAGMM 在目标函数中去除样本能量函数获得的变量，这个DVAGMM 变体相当于1个深度自动编码器。为确保压缩网络训练良好，实验采用预训练策略［30］在PAE中的样本重构误差作为异常检测的度量标准。

在第一组实验中，随机选择50%的数据进行训练，而将剩余的50%数据用于测试，保证用于训练模型的样本都为正常样本，并且所有方法都运行20次，取平均值，得到如表4所示的结果。

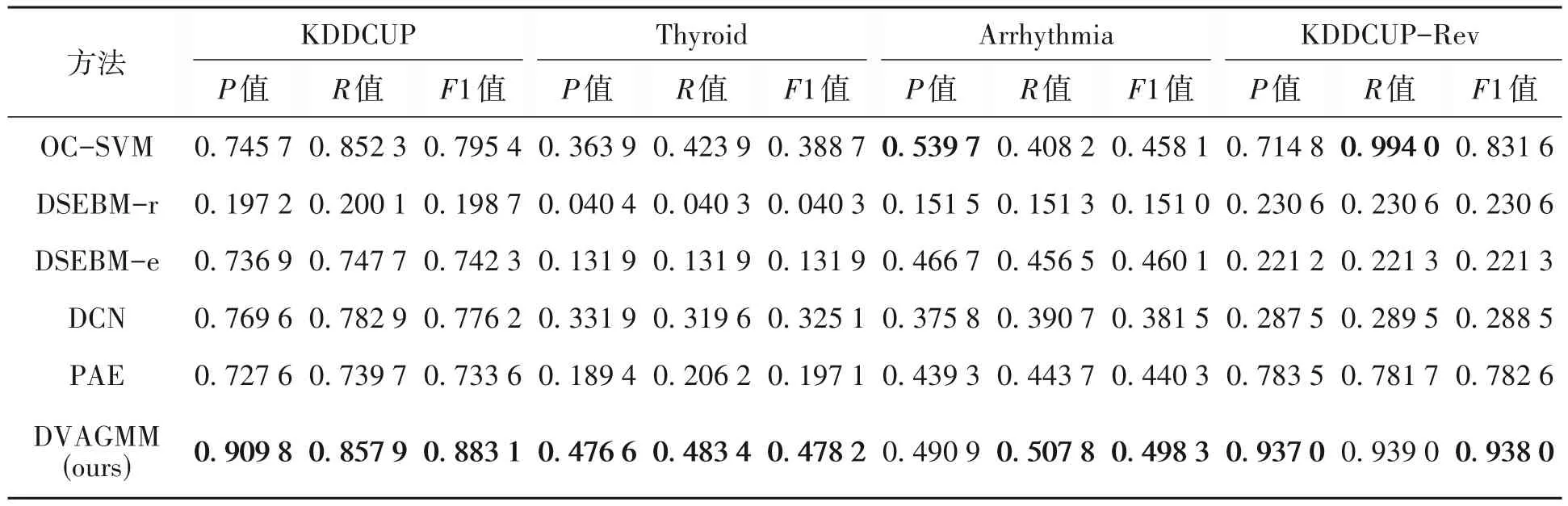
表 4 DAGMM与多个异常检测算法的比较Table 4 Comparison of DAGMM with multiple anomaly detection algorithms

第二组实验针对KDDCUP 数据集，仍然将50%的数据用于训练，剩余50%的数据用于测试。为了研究训练时异常样本数量对训练模型的干扰，第二组实验将异常样本和正常样本按混合比例c进行混合作为训练集，对各个模型进行训练，获得的实验结果如表5所示。

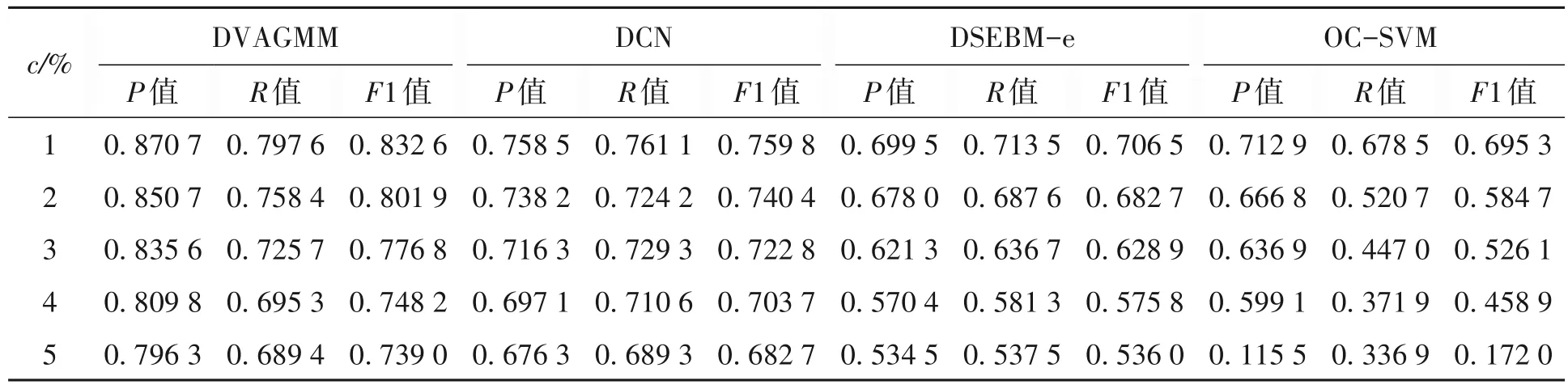
表 5 异常样本比例对各模型训练的影响情况Table 5 Effect of anomaly sample proportion on training by model

从表4可见，DVAGMM 在准确率P、召回率R、以及F1指标等多个方面相较于其他流行的异常检测算法及其变体都有着优异的表现。在KDDCUP和KDDCUP-Rev数据集上，DVAGMM 表现更加突出。相比于OC-SVM、DSEBM-e、DCN 及PAE 模型，DVAGMM 在准确率方面分别高出了16.41%、17.29%、14.02%和18.22%。在召回率指标上，DVAGMM 也有着不错的表现，仅在KDDCUP-Rev 数据集上略低于OC-SVM，在KDDCUP、Thyroid 和Arrhythmia 数据集上比OC-SVM 分别高出0.56%、5.95%、9.96%。说明在异常检测过程中，DVAGMM 能够尽可能地检测出异常样本。对于DSEBM 的变体，由于其只考虑部分损失，召回率指标普遍较低，说明在实际应用中对异常样本不敏感。在4个数据集上，DVAGMM 的F1 指标均超过OC-SVM，分别高出8.77%、10.64%、8.95%和4.02%，表明在综合性能上，DVAGMM相较于其他异常检测算法有着明显的优势。

分析第一组实验发现，DVAGMM 在异常检测和信息判别方面都有着出色的效果。尽管OC-SVM在某些情况下表现不错，但其容易受到数据维度的限制；而DSEBM 的变体虽然在不同数据集上表现良好，但DVAGMM 共同考虑了重构误差和样本能量，性能更佳。DCN 和PAE 模型在预先训练的深度自动编码器方面可能存在限制，且当预训练较为成熟时，这些模型难以适应数据维度的减少，从而影响后续的密度估计任务。

分析第二组实验发现，被异常数据污染的训练集会对检测准确性产生影响，随着异常样本的混合比例从1%增加到5%，所有方法的准确率、召回率和F1 指标都下降了。不过，DVAGMM 在5%的样本污染状态下仍然保持了不错的检测效果。相比之下，OC-SVM 对训练集污染比例更为敏感。因此，在训练时最好使用低污染的数据集。

综上所述，DVAGMM 通过端到端的训练，在公共基准数据集上表现良好，能够有效提高无监督异常检测的检测效果。

3 结论

针对高维数据无监督异常检测难以重构异常样本，无法保留低维空间信息的问题，本文提出了深度变分自编码高斯混合模型DVAGMM，通过压缩网络和估计网络进行端到端的训练，联合优化了深度变分自编码器和高斯混合模型的参数。实验结果表明，在异常检测方面，DVAGMM 模型相较于其他几个流行算法有着明显的优越性，在综合性能上高出第二名4.02%，对于训练样本的污染情况也有着较强的抵抗性，在5%的样本污染率下依旧能保持80%的准确率。后续将考虑通过加入粒化的思想，引入粒计算的理念来增强模型的泛化性能，并进一步提高异常检测的准确率。