基于Freeman全极化分解的干雪识别指数模型构建

黄 林，李 晖，康 璇

（厦门理工学院计算机与信息工程学院，福建 厦门 361024）

积雪是冰冻圈内分布最为广泛且最为活跃的要素，在水文循环、雪灾预测等方面具有重要作用［1］。目前，使用光学遥感数据进行积雪研究易受多云多雨的影响［2］，而合成孔径雷达（synthetic aperture radar，SAR）能够穿透云层，具有全天候、全天时成像的特点，在山区积雪识别及分类应用中具有极大的潜力［3］。全极化SAR数据可以反映积雪的极化散射特性，区分地物的散射机制，为积雪识别提供了丰富的极化信息，有助于提高积雪识别的精度［4］。从SAR图像中提取有效的极化特征对积雪特性研究和分析具有重要意义。同时，积雪极化特征的提取也是SAR 图像识别的关键技术，对积雪的准确识别起着重要作用［5］。

国内外学者利用遥感数据对积雪识别方法进行了大量的研究。庞海洋等［6］基于Landsat8 OLI数据源，综合考虑蓝紫光、蓝光、绿光和短波红外波段，提出了增强型归一化差值雪指数（enhanced normalized difference snow index，ENDSI）。高扬等［7］对青藏高原地区不同土地覆盖类型下判识积雪的最优归一化积雪指数（normalized difference snow index，NDSI）阈值进行了研究，表明不同土地覆盖类型下的NDSI 阈值优化可以有效提高青藏高原积雪判别精度。马腾耀等［8］利用GF-3 全极化SAR 数据，提出了一种基于特征优选的积雪识别方法。Varade等［9］提出了一种使用全极化SAR数据评估熵（H）和各向异性（A）绘制积雪的新指标，并将其称为雷达雪分数（radar snow fraction，RSF）。王光远等［10］基于高分六号（GF-6）多光谱相机（PMS）影像的目视解译结果，结合光谱特征规律，探讨了深度学习、决策树等算法的积雪信息识别。康璇等［11］对SAR 数据极化特征和散射特征进行组合，采用随机森林算法对积雪进行了识别提取。目前，基于积雪指数的研究主要使用光学遥感数据，而使用SAR 数据构建指数的研究较少。其他领域的SAR 遥感指数研究主要是通过不同极化后向散射系数的数学组合［12-14］，或是基于SAR 数据的后向散射系数结合光学遥感指数的反演模型研究［15-19］，其中使用的方法主要还是机器学习方法［20-21］，但利用极化分解技术获得不同散射机理的后向散射分量，进而构建物理意义更加明确的SAR 遥感指数的研究还较少［22］。因此，对于单一极化分解获取的极化特征的信息提取还有很大的提升空间，如何利用较少的散射信息识别积雪范围仍需进一步探索。

基于模型的分解直接与地物真实散射机制相关联，具有一定的物理意义。Freeman 分解是第一个被提出的基于模型的分解［23］，相对于其他分解方法，Freeman分解更符合地物的散射机制，对地物散射特征描述得更加充分［24］。基于此，本文对全极化SAR数据进行Freeman分解，通过极化特征值在积雪与非积雪面的特征，构建一种新的指数进行干雪识别。

1 研究区概况及数据源

1.1 研究区概况

以新疆天山中段北麓玛纳斯河流域（43.79°N～44.09°N，85.74°E～86.13°E）作为研究区，地表覆盖物主要为草地，气候属于中温带大陆性干旱气候，总体降水量较少，受水汽来源、地形和高程影响较大。根据自然高度带，研究区可划分为3 带：50%以上区域海拔高度在0～1 300 m，为草原至半灌木过渡带；南部约25%地区海拔在1 300～2 000 m，为地草甸草原带；最南部少部分地区海拔在2 000～2 700 m，为云杉林带［25］。2013 年12 月12 日至2013 年12 月16 日期间，在研究区内开展了为期5 d 与Radarast-2 卫星SAR 数据同步的地面积雪实地观测，获取研究区观测点的雪深、海拔、坡度、气温、下垫面等信息，根据实地观测，研究区积雪深度范围介于0～20 cm。

1.2 数据源及预处理

获取2013年12月13日的Radarsat-2全极化数据，包括HH、HV、VV、VH 4种极化方式，为单视复数数据（single look complex，SLC）C 波段产品，距离向和方位向分辨率分别为4.733 m 和4.799 m，中心入射角为43.45 °。结合实地观测和天气情况，对应积雪状态为干雪。同时，选择2013 年10 月6日的Landsat-8 OLI 数据（无雪期）、2013 年12 月14 日的GF-1 WFV 数据（干雪期）辅助参考。无雪期数据用于与积雪期数据对照判断积雪区域及积雪区下垫面，干雪期数据用于同一时期SAR 数据的积雪判断与精度评价参考。查询历史天气记录（https：//lishi.tianqi.com）可知，2013年12月13—14日温度均在0 ℃以下，未有降水（降雪）记录，说明干雪期SAR 数据和干雪期GF-1 WFV 数据在地表覆盖类型上具有一致性。

为保证与光学遥感数据空间分辨率（20 m）相近，对Radarsat-2数据的距离向和方位向分别采用3×3 多视处理。对于全极化Radarsat-2 数据，相干斑滤波不仅需要考虑4 个通道（HH、HV、VH、VV）的滤波，还要考虑各个通道之间的相关性。因此，选用Refined Lee 滤波算法进行斑抑制，滤波窗口设置为5×5。最后，选择影像对应的DEM数对影像进行地理编码，本文选用NASA提供的90 m分辨率数据STRM4 DEM（https：//srtm.csi.cgiar.org/）对影像区域进行地理编码操作，将影像从斜距几何转换为地图投影坐标。

2 研究方法

2.1 Freeman极化分解、极化特征获取与指数构建

在散射过程中，对SAR 目标极化效应进行定量描述的常用方法是运用极化散射矩阵，它包含目标的全部极化信息，其定义为

式（1）中：S表示单个像素散射特性；Shh、Svv表示同极化项；Shv、Svh表示交叉极化项。

极化协方差矩阵同极化散射矩阵一样，包含雷达测量得到的全部目标极化信息。对于互易介质Shv= Svh，极化散射矩阵矢量可表示为以3×3 的视矩阵为例，协方差矩阵C 定义为

式（2）中：*表示共轭矩阵；T表示矩阵的转置；|·|表示矩阵的模；〈·〉表示随机散射介质在各向同性下的空间统计平均。

极化分解可以基于散射矩阵、相干矩阵或协方差矩阵实现［26］。全极化SAR 图像通常使用9 个独立参量表示接收到的数据，从而构成协方差矩阵或者相干矩阵，二者是等价的，都是非负定Hermitian矩阵［27］。Freeman分解以极化协方差矩阵为分解对象，将地物分为体散射、面散射和二面角散射3 类散射机制［28］。相对于其他分解方法，Freeman 分解更符合地物的散射机制，对地物散射特征描述得更加充分。3类散射方式的协方差矩阵分量为

式（3）～式（5）中：C1为面散射对应的协方差矩阵分量；C2为二面角散射对应的协方差矩阵分量；C3为体散射对应协方差矩阵分量；fs、fd、fv为各分量贡献值；α、β为各种散射方式下极化散射矩阵分量中水平极化波与垂直极化波的比值。总的极化协方差矩阵可表示为

由式（1）～（6）可解出未知量的值，并得到3类散射分量的功率为

式（7）～式（9）中：Ps、Pd、Pv分别为散射、二面角散射和体散射各分量的散射功率。

极化分解后获得的极化参数，都可作为积雪识别过程中的一个特征［29］。基于极化参数在覆盖与非覆盖区的不同散射机理，选取可以较大程度增加积雪与非积雪间差异的极化特征以构建归一化指数。

2.2 Ostu阈值分割

Ostu 算法［30］是由日本学者大津提出的，也称最大类间方差法，是图像分割领域的经典算法。Ostu 算法的思想是：根据直方图确定阈值t，将灰度图像分成背景和前景2 部分，前景与背景的类间方差越大，说明两者的差别越大［31］。若大小为m×n的图像，设图像中像素的灰度值小于阈值t的像素个数为n0，大于阈值t的像素个数为n1，则有

由式（10）～式（13），类间方差g（t）可表示为

式（10）～式（14）中：ω0为背景像素点所占比例；ω1为前景像素点所占比例；μ 为图像灰度值；μ0和μ1分别为背景和前景的均值。通过不断对阈值t进行遍历，当g（t）取得最大时，类间方差最大，即错分概率最小，此时t即为最佳阈值。

本文中，通过Ostu 自动阈值分割算法确定阈值t，将小于阈值的像素点记为非积雪点，将大于阈值的像素点记为积雪点，对得到的积雪指数模型进行分割，以达到积雪识别的目的。

2.3 监督分类与精度评价

在遥感图像监督分类中，距离法和最大似然法是较常用的2种方法。本文选用最小距离、马式距离和最大似然分类方法对研究区进行分类，获得积雪与非积雪。

在阈值分割和监督分类之后，本文以同一时期的GF-1 WFV 数据作为参考，随机选择积雪区域与非积雪区域各10 个进行精度评价，共130 541 个像元，其中积雪像元70 952 个，非积雪像元59 589个，对识别结果建立混淆矩阵。以总体精度（overall accuracy，OA）、Kappa系数（Kappa coefficient）、用户精度（user’s accuracy，UA）和制图精度（producer’s accuracy，PA）对识别结果进行精度评价。总体精度可以分析整体精度效果，Kappa系数可以确定积雪识别结果与真值的一致性，用户精度和制图精度可以体现误分率和漏分率。

3 实验结果与分析

3.1 Freeman极化分解特征分析

Freeman 极化分解后的极化特征为Freeman_Dbl、Freeman_Vol和Freeman_Odd，分别表示二面角散射、体散射和面散射，图1 为研究区Radarsat-2 全极化数据Freeman极化分解后结果。

由于研究区积雪深度范围介于0～20 cm，相对较浅，C波段的电磁波可以在雪表面发生折射，并穿透干雪。当有积雪覆盖时，在干雪条件下，主要散射为雪-地界面的面散射，雪层体散射比总体面散射少［32］，结合光学遥感数据可知，积雪覆盖区表现为蓝紫色。无雪覆盖区主要出现在高覆盖度草地和林地，主要散射为植被体散射，图像呈绿色。

3.2 基于Freeman极化分解的FSCI_Vol_Dbl构建

在Freeman 极化分解的图像中，选择干雪期积雪覆盖区域与非积雪覆盖区域，分别统计各散射特征的概率分布密度，结果如图2 所示。由图2（a）可知，在积雪覆盖区，3 个散射分量的分布由小到大分别是二面角散射、体散射和面散射；二面角散射介于-29～-21 dB，主要集中在-25 dB；体散射介于-22～-14 dB，主要集中在-19 dB；面散射介于-20～-5 dB，分布特征呈高原形，数值较不集中。因此可知，二面角散射分布较为集中，且与体散射、面散射均存在较高的可分离性；体散射普遍小于面散射，且由于积雪覆盖较浅，体散射和面散射无法直接分开，有较多区域混合在一起。由图2（b）可知，2个散射分量的分布由小到大的分布是二面角散射、面散射和体散射；二面角散射介于-29～-15 dB，主要集中在-24 dB；体散射主要集中在-8 dB，且普遍比面散射大；面散射分布进一步扩大，分布范围介于-20～-1 dB之间。

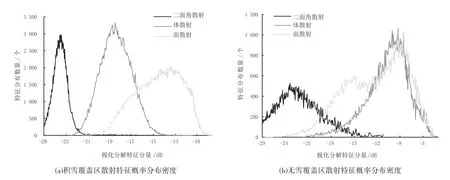
图2 干雪期积雪区与非积雪区散射特征概率分布密度Fig.2 Sampling histogram of snow covered area and non snow covered area in dry snow period

对比图2（a）和图2（b）发现，积雪区体散射小于非积雪区的体散射，面散射在积雪区与非积雪区均呈高原型；由数值大小坐落范围分析可知，二面角散射与体散射、面散射均存在较好的分离度，但二面角散射与体散射均分布较为集中。因此，基于二面角散射与体散射的规律，将二面角散射与体散射构建差值指数为

式（15）中：FSCI_Vol_Dbl表示由体散射、二面角散射计算的积雪覆盖度结果；Freeman_Vol为Freeman 的体散射；Freeman_Dbl为Freeman 的二面角散射。FSCI_Vol_Dbl通过积雪区与非积雪区体散射与面散射的特点，计算出的范围为-1.0～0，一般越接近于0，亮度值越高，积雪覆盖度越高。

同时，为了进一步验证选择二面角散射与体散射优于其他分量构建指数，在干雪期，本文从其他分量呈现出的规律，构建了另外2种积雪范围识别指数。

1）基于面散射、体散射在积雪与非积雪区的规律，选择面散射、体散射分量做差值，构建指数为

式（16）中：FSCI_Vol_Odd表示由面散射、体散射计算的积雪覆盖度结果；Freeman_Vol为Freeman 的体散射；Freeman_Odd为Freeman的面散射。

2）基于二面角散射与面散射的规律，选择二面角散射、面散射做差值，构建指数为

式（17）中：FSCI_Odd_Dbl表示由面散射、二面角散射计算的积雪覆盖度结果；Freeman_Odd为Freeman 的面散射；Freeman_Dbl为Freeman的二面角散射。

3.3 利用FSCI_Vol_DBl进行积雪识别的分析与比较

3.3.1 3种指数积雪识别对比

将3 种指数得到的结果与GF-1 WFV 影像、NDSI 进行比较，基于Freeman 分解特征分量的指数构建结果与对比如图3 所示。NDSI 利用积雪在光谱的可见光部分比短红外波段更高反射率的特点，使用绿色和短红外波段进行计算，范围为-1.0～1.0，值越接近于1，亮度值越高，积雪覆盖度越高。由于同时期获取的GF-1 WFV 数据只有4 个波段，缺少计算NDSI 所需的短红外（SWIR）波段，且该时期GF-1 WFV 数据北部被大量云层覆盖，因此，本文同时利用同时期的GF-1 WFV 影像（见图3（a））、2013 年12 月9 日的Landsat-8 OLI 数据计算的NDSI（见图3（b））与FSCI_Vol_Dbl结果进行比较。由于Landsat-8 OLI得到的NDSI比GF-1 WFV数据提前5 d，因此会存在一定误差。

图3 基于Freemman分解特征分量的指数构建结果与对比Fig.3 Index construction results and comparison based on Freeman decomposition feature component

图3（c）为FSCI_Vol_Dbl的结果，可见，利用二面角散射与体散射构建的指数在积雪覆盖区的灰度值远远高于非积雪覆盖区，可以通过亮暗差异反映积雪覆盖；图3（d）为FSCI_Vol_Odd的结果，可见，构建的指数在积雪覆盖区与无雪覆盖区亮度差异并不明显，在积雪区与非积雪区无法通过灰度值大小直观反映出积雪覆盖；图3（e）为FSCI_Odd_Dbl的结果，可见，展现出的积雪覆盖效果较不理想，主要原因是面散射的概率分布范围较宽，密度较不集中，无法较统一地将积雪与非积雪的差异增大。

由图3的结果对比可见，利用二面角散射与体散射构建的指数是积雪覆盖度的最佳指示因子，增大了积雪与非积雪的差异，突出了积雪范围。

FSCI_Vol_Dbl与Landsat-8 OLI数据计算的NDSI相比，两者在研究区内积雪与非积雪区轮廓较为明显，二者颜色分布较为相似。与GF-1 WFV数据相比，FSCI_Vol_Dbl中积雪区/非积雪区体现的差异比NDSI大，NDSI数据中整个研究区内亮度值均较高，存在较大的积雪高估范围。FSCI_Vol_Dbl利用Freeman极化分解后的特征分量，通过非线性变换，增强了FSCI_Vol_Dbl低值部分，并抑制了高值部分，使得FSCI_Vol_Dbl数值较一地达到饱和状态，从而对高覆盖度积雪区敏感度降低。因二面角散射与体散射均为负值，计算出FSCI_Vol_Dbl的值为负数，在-1～0，避免了数据过大或过小给数据分析造成影响。此外，FSCI_Vol_Dbl还能够消除部分山区积雪识别易受云层覆盖限制的影响。由于Freeman 极化分解获取的特征分量为体与面的散射，极易受地形因素影响，计算得出FSCI_Vol_Dbl的值接近-1，一般表示为地势起伏较大的山地，地形复杂，使得出现小于-1 的异常值。FSCI_Vol_Dbl的值接近0，一般表示为该地区为积雪覆盖。

确定积雪与非积雪间的阈值，通过数值的比较，即可判断积雪与非积雪，快速提取积雪空间分布信息。本文利用Ostu 阈值分割算法对FSCI_Vol_Dbl得到的阈值结果为-0.246。以-0.246 为阈值确定的积雪与非积雪区，具体如图4 所示。由图4 可见，FSCI_Vol_Dbl识别结果与GF-1 WFV影像中积雪范围相似，可以识别积雪。

图4 FSCI_Vol_Dbl阈值分割结果Fig.4 Threshold division result of FSCI_Vol_Dbl

3.3.2 与监督分类结果比较

图5 为利用FSCI_Vol_Dbl进行监督分类的干雪识别结果。其中，图5（a）、图5（b）、图5（c）分别为FSCI_Vol_Dbl以最小距离、马氏距离和最大似然法得到的积雪识别结果。

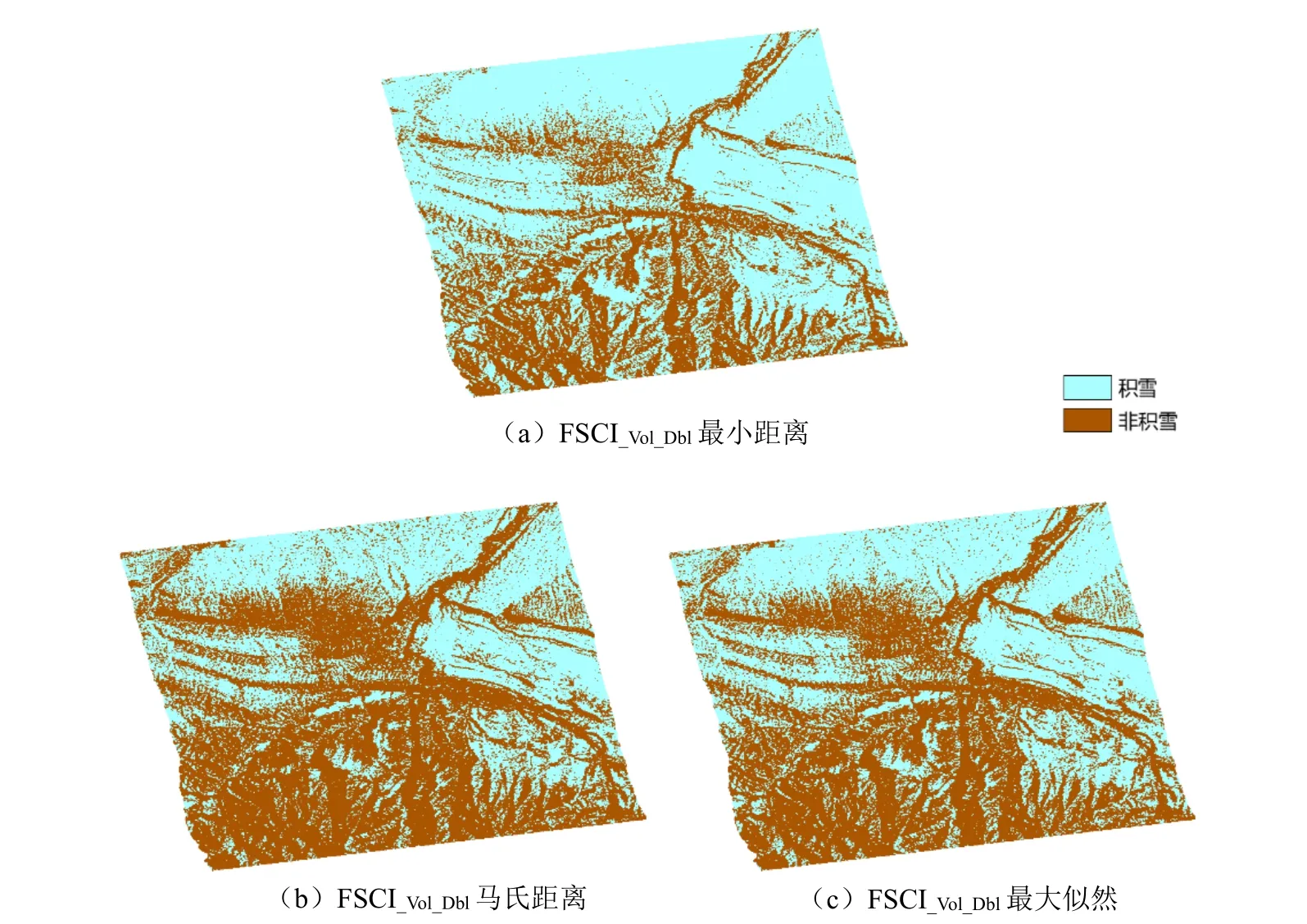
图5 监督分类积雪识别结果Fig.5 Snow cover recognize results of supervised classification

由图5可见：整体上，3种监督分类方法都完成了积雪范围的识别，且范围与光学遥感影像相近。其中，在光学数据北部被云覆盖的地区（图3a），SAR 数据可以减轻云层的影响，达到了识别效果。从分类方法上分析，FSCI_Vol_Dbl的最小距离分类对积雪识别的范围斑块化较少，结果较平滑，但存在部分非积雪覆盖地区误分为积雪地区，易误判的地区集中在山区的背阴面及地形起伏较大的地区；马氏距离分类的结果较零碎，积雪识别的范围在所有方法中最小，积雪地区存在较多非积雪斑块；最大似然分类的结果与马氏距离相近，但识别的积雪零碎斑块比马氏距离少。研究区南部地区地势较高，地形复杂，该地区的识别结果在最小距离分类的结果中与马氏距离、最大似然分类结果差异较大。

表1 为混淆矩阵精度评价结果，精度评价中将FSCI_Vol_Dbl阈值分割的结果（图4）与所有监督分类结果（图5）比较。从OA 和Kappa 系数上看，利用本文提出的FSCI_Vol_Dbl进行积雪识别的精度介于80%～90%，Kappa 系数介于0.60～0.80，呈现出高度的一致性。通过FSCI_Vol_Dbl阈值分割的精度比最小距离监督分类精度高3.73%，比马氏距离监督分类精度高0.9%，与最大似然分类结果相当。从UA和制图精度（PA）分析，FSCI_Vol_Dbl阈值分割的结果UA 高于PA，可见，通过FSCI_Vol_Dbl指数阈值分割识别积雪对积雪像元的判断高于非积雪像元。

表1 混淆矩阵精度评价结果Table 1 Precision evaluation of confusion matrix

4 结论

对新疆玛纳斯河流域全极化SAR 数据通过极化分解技术，获得不同散射机理的后向散射分量，根据概率分布密度在干雪期积雪覆盖面与非积雪覆盖面极化特征的规律，构建了基于极化分解的干雪识别指数模型。结果表明，基于极化分解的极化特征分量受到积雪覆盖影响，通过增大不同散射机理的数值差构建指数模型，利用阈值可划分积雪/非积雪范围，总体精度为85.83%，Kappa 系数为0.716，具有一定的准确性，在进行山地积雪识别时具有一定的参考意义。

同时，由于受山地地形环境复杂、植被类型多样、其他大气状况、积雪本身的晶体状态及下垫面等因素的影响，SAR指数的适用范围往往具有一定的地域性和时效性，本文指数是否适合其他区域的研究还需要进一步验证。后续将综合地形等因素，充分利用获取的散射特征，构建从机理层次与积雪紧密联系的指数进行研究。