两种极地压实雪层跑道设计方法

霍海峰 李涛 陈庆炜 贾汶韬 胡彪

(1 中国民航大学交通科学与工程学院, 天津 300300;2 交通部机场工程安全与长期性能科研基地, 天津 300300)

0 引言

南极洲具有丰富的自然资源[1], 也是全球环境变化的驱动器、气候变化的冷源, 已成为世界各国科学考察的热点区域, 而极地跑道是科考后勤保障的重要基础设施。传统的机场跑道设计方法分为刚性道面设计[2]和柔性道面设计[3]两类。极地环境地形复杂、气候恶劣, 且材料运输困难, 使得传统道面建设在极地条件下难以实现。而因地取材, 将冰雪作为场道材料建造跑道成为必然选择。

冰雪跑道可分海冰跑道、蓝冰跑道、雪橇跑道和压实雪层跑道4 种[1], 其中冰跑道设计与刚性跑道设计原理相似, 雪跑道设计与柔性跑道相似[4]。孙波等[1]研究指出压实雪层跑道是我国在南极建造满足重型轮式飞机起降跑道的最优选择。南极的雪层多是附着在冰上的, 压实雪层跑道是以冰上积雪作为道基和道面建筑材料, 利用人工压实提高雪的密度, 之后通过烧结增强雪层强度。其中, 烧结作用是指雪颗粒升华—冷凝—重结晶—体积扩散并与周围颗粒形成新的胶结体、强度增长的过程。

早在20 世纪中期, 美国、俄罗斯等国便展开了深入研究, 而强度是雪跑道设计重要的指标。影响雪强度的因素很多, 如烧结、应变率、温度、粒径分布和密度等[5]。Ramseier 和Keeler[6]研究得出烧结是指雪晶升华—冷凝—重结晶的过程,雪晶升华为水蒸气, 在温度梯度的作用下水蒸气由暖区向冷区迁移, 在迁移过程中水蒸气冷凝于雪晶表面并向周围扩散, 固化为冰并与相邻的雪晶形成胶结。Jellinek[7]探究了雪的年龄、颗粒大小以及制备时间与抗压强度的函数关系，发现雪龄越长、雪颗粒的尺寸越小, 制备雪样的时间越短，其抗压强度也就越低。Golubev 和Frolov[8-9]提出并建立了雪结构模型, 可以通过该模型来评估雪的力学性能, 如杨氏模量、强度、泊松比等。Hagenmuller 等[10]模拟得到雪的抗拉强度与密度之间的关系, 发现雪的抗拉强度随雪密度减小而降低。Ramseier[11]认为雪的强度在接近融点时进行烧结将会达到最佳, 且烧结过程随着温度的降低会减缓。洪嘉琳等[12]在人工压实雪层上进行循环荷载的作用, 发现在一定范围内, 循环荷载可以强化雪层的抗压强度, 超出该范围后循环荷载会削弱雪层的抗压强度。Hong 等[13]研究得出经过压实后的高密度雪, 其烧结速度更快, 可以通过高压烧结雪来改善冰雪工程。

在对南极地区雪的性质深入认识基础上, 众多冰雪跑道相继建成。1990 年美国在麦克默多站附近的罗斯冰架上建造了第一条压实雪层跑道[14]。澳大利亚在威尔克斯地(Wilkes Land)建设了威尔金斯蓝冰跑道(Wilkins Runway), 跑道表面铺有压缩雪[4]。美国在麦克默多站建立的南极洲凤凰跑道为6 层压实雪层跑道, 可供满载的C17 重型运输机起降[4], 这也是目前最重的轮式飞机在压实雪层跑道起降的案例。

可以看出, 国外针对雪跑道的研究已积累了丰富的经验, 而我国关于雪跑道的报道却很少。本文重点介绍两种雪跑道设计方法, 分别是双层弹性体系法(简称“双层弹性法”)和实测经验法(简称“经验法”), 双层弹性法是将雪跑道假设为雪道面和雪地基两层弹性结构, 利用Burmister 理论计算道面弯沉。经验法是通过现场试验, 统计弯沉值与单轮载重、胎压和轮印半径的关系。鉴于我国在压实雪层跑道设计方面研究较少, 本文详细介绍了上述两种压实雪层跑道的设计方法, 以A320 机型为例进行压实雪层跑道设计, 对比了两种设计的道面指标, 并对其优势和局限进行分析。本文的研究成果可为我国极地压实雪层跑道的设计提供借鉴和参考。

1 雪的物理力学指标换算关系

在压实雪层雪跑道设计过程中, 强度指标和变形指标是设计的基础。已有文献[15-16]常用3 个指标来表征雪的强度, 分别是RAM 硬度指标R、无侧限抗压强度fu和加州承载比指标CBR(C)。其中硬度指标R可反映雪层密实化程度, 其利用雪地贯入仪对积雪实施冲击, 具体说明见Abele的研究报道[17]。无侧限抗压强度获取的过程是利用专用工具将雪样从现场取出, 雪样通常为圆柱体, 其高与直径之比约为2.5, Ramseier[11]所取雪样平均高度为180 mm, 平均直径为75 mm, 然后用无侧限压缩仪现场试验获得抗压强度。雪层CBR值的获取方法与传统道路一致, 这里不再赘述。

Abele[15]系统总结了上述3 种强度指标的关系, 发现各指标间具有一一对应关系。他对比多个格陵兰冰盖天然雪样RAM 硬度指标R与无侧限抗压强度指标fu的试验数据, 认为Brunke[18]试验数据及拟合公式较为合理。无侧限抗压强度fu与RAM硬度R关系如公式(1)所示:

式中,fu为无侧限抗压强度, 单位为kg·cm-2;R为RAM 硬度, 单位为kg。Abele[15]表示公式(1)适用于高密度雪层无侧限抗压强度fu与RAM 硬度R间的变换。

Abele 等[19]在美国密歇根州通过试验得出CBR与RAM 硬度的关系, 并拟合出硬度指标R与CBR 两者之间的关系式(2)[15]:

式中,C的单位为%。

3 种强度指标对应关系如图1 所示。

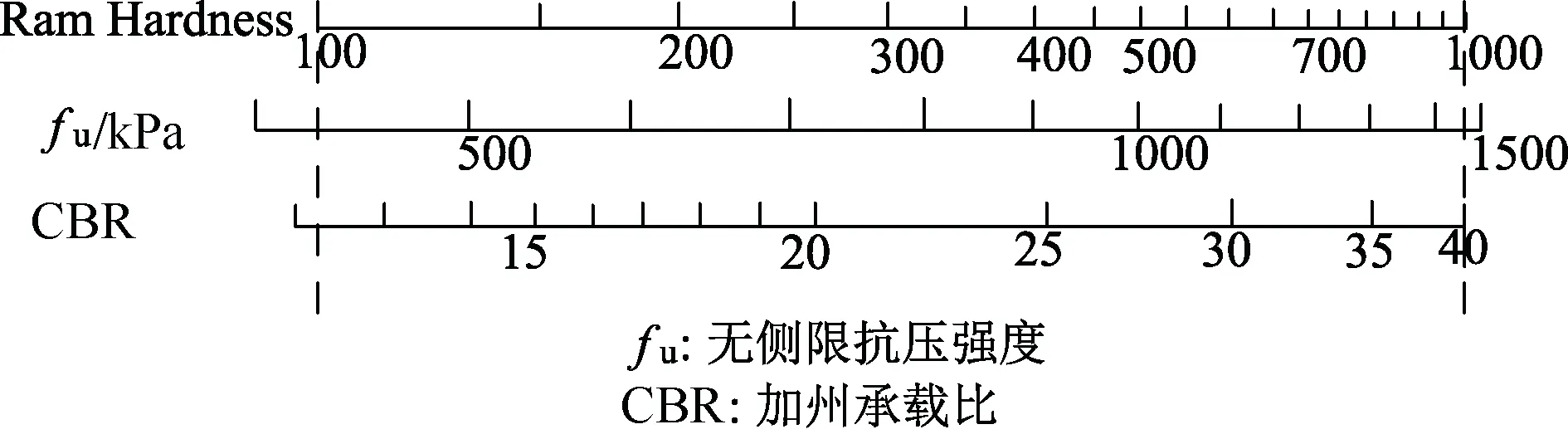
图1 不同强度指标换算关系[15]Fig.1. Conversion relationship of different strength indexes[15]

雪的变形指标通常用弹性模量E表示, Russell-Head 等[20]统计了大量试验数据, 建立了变形指标E和强度指标CBR 间的关系, 如公式(3)所示:

式中,E为弹性模量, 单位为MPa。该公式适用于温度-10～1℃完全烧结的雪层。该式与公式(1)和公式(2)联立, 可建立E与R或fu间的关系。

雪的强度发展是一个很复杂的过程, 其与压实雪的密度、环境温度和烧结时间等因素有关, 一般认为雪在充分烧结后稳定并达到最终强度。Haas 和Bott[21]认为烧结完全后雪的最终强度只与初始密度有关, 他们在美国密歇根州对人工处理过不同密度的雪进行CBR 试验, 并参考大量格陵兰岛积雪CBR 与密度的数据, 拟合出公式(4):

式中,ρ为雪的密度, 单位为g·cm-3。公式(4)适用于烧结完全后雪CBR 与密度的换算。

Russell-Head 等[20]对两者间联系也做了统计,经验公式(5)由澳大利亚南极凯西站的跑道上原位试验数据进行最小二乘拟合得到:

式中, 温度为-5～-1℃。

通过公式(5)可以将压实雪的密度与CBR 建立联系, 进而和R、fu以及E建立联系。因此, 设计中对强度变形指标的要求, 可以通过控制雪层的密度来实现。公式(5)与公式(4)有所不同, 由于公式(5)样本数据较少, 普遍采用公式(4)作为CBR 与密度的换算公式。

2 双层弹性体系法

2.1 设计依据与思路

双层弹性体系法是设计压实雪跑道的一种常用方法, 其是将雪跑道假设为雪道面和雪地基双层弹性结构, 利用Burmister[22]理论计算道面弯沉,进而获得道面设计参数。其中, Burmister 理论是以弹性理论为基础, 研究得出双层弹性系统中应力和位移理论, 可快速地计算道面弯沉。

其设计思路为, 将压实雪层跑道作为双层弹性结构, 已知两层的泊松比μ以及下层的弹性模量E2, 设计目标拟得到针对某种机型的雪道面厚度h和CBR。

首先假设上层雪道面的厚度和弹性模量, 基于Burmister 理论计算出道面弯沉, 并建立弯沉与道面厚度和弹性模量的关系。将某道面弯沉值作为设计标准, 并根据现场环境确定道面的厚度和CBR。由上一节可知, 最终强度CBR 在一定温度下与雪的密度相关, 施工中可控制雪层密度达到设计目标。

双层结构的参数分别为: 弹性模量E1和E2,单位为MPa; 泊松比μ1和μ2; 胎压p, 单位为kPa;轮印半径r, 单位为mm。跑道结构如图2 所示, 弯沉量计算如公式(6)所示:

式中,S为道面表层弯沉;p为胎压;r为轮印半径;E2为下层雪跑道弹性模量。

图2 双层雪跑道结构图Fig.2. Structure of double snow runway

2.2 设计过程

1. 确定飞机设计参数和下雪层的弹性模量,双层结构的泊松比均取0.35。

2. 取不同上层雪道面的厚度h, 得到对应的厚度与轮印半径之比h/r; 取不同上层雪道面弹性模量为E1, 计算对应的CBR。

3. 通过双层结构弯沉影响系数图[22], 读取不同h/r与E1/E2对应的道面弯沉影响系数F。双层结构弯沉影响系数图如图3 所示。

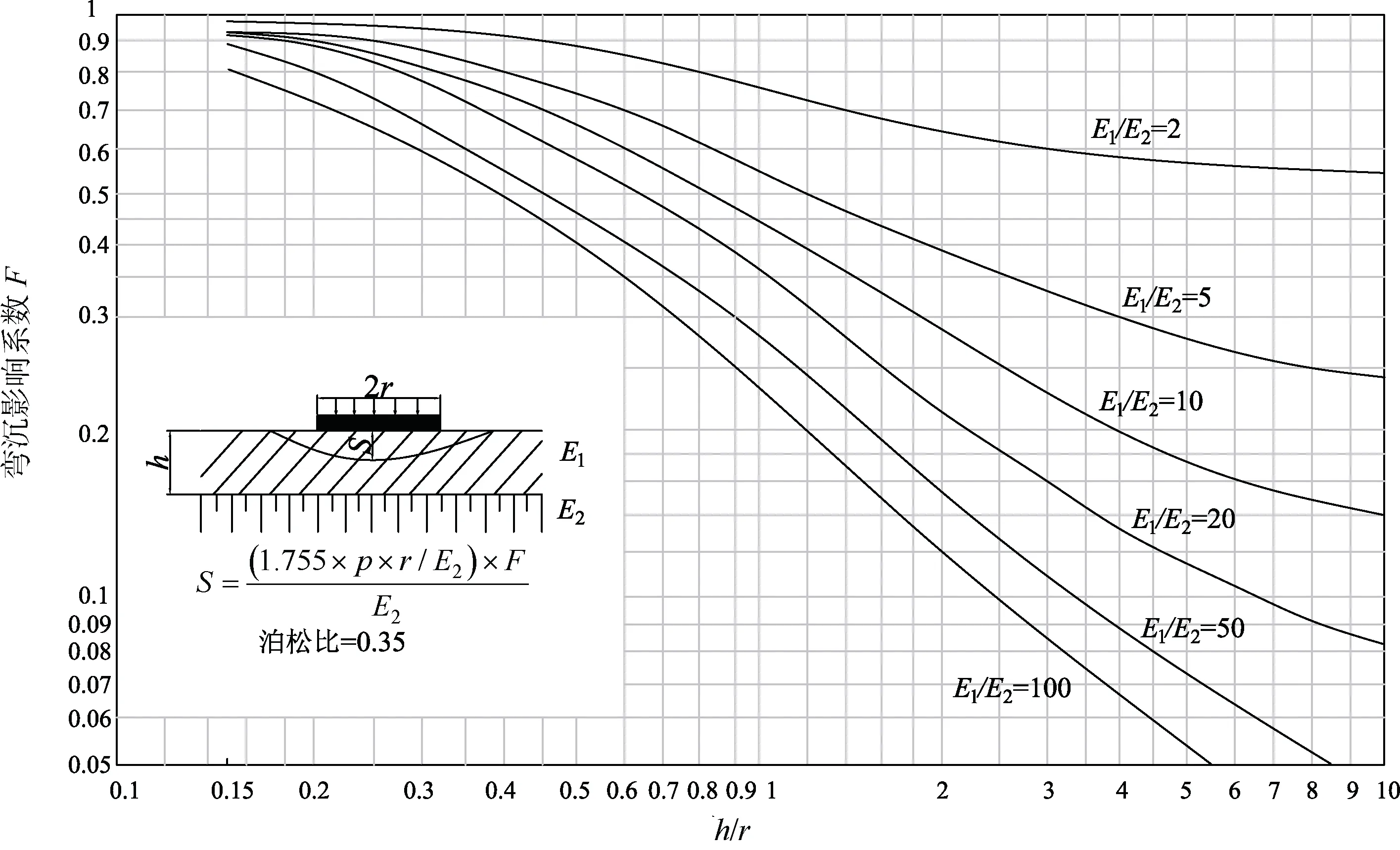
图3 弯沉影响系数曲线[20]Fig.3. Settlement influence coefficient curve[20]

4. 根据弯沉公式(7), 计算不同h与CBR 组合的道面弯沉:

5. 绘制给定上层CBR 下, 道面弯沉S和上层道面厚度h关系图; 绘制给定上层道面厚度h下,弯沉S和上层道面CBR 图。

6. 确定若干道面弯沉值在不同CBR 下的厚度h; 确定若干道面弯沉值在不同厚度h下的CBR。

7. 绘制道面弯沉图, 横轴为道面CBR, 纵轴为道面厚度h。

在第7 步中, 对于给定的弯沉设计标准, 将会对应多个h和CBR 的组合, 如何选取厚度和强度组合需要根据现场条件。White 和Mccallum[4]表明, 较高的环境温度有助于雪层的压实, 在-5～0℃之间, 压实雪层密度很容易达到0.6 g·cm-3以上; 当温度较低时, 需要进行特殊处理。故当环境温度较高时, 可选择高 CBR 低厚度的组合; 当温度较低时, 由于雪层不容易压实, 可选择低CBR 高厚度组合。

2.3 设计案例

步骤1:飞机和雪层地基参数。本次案例分析采用了空客A320 机型对压实雪层跑道做设计。该机型设计参数为: 最大起飞重量754.6 kN; 起落架为双轮双轴, 主起落架总轮数4; 胎压p=1.14×103kPa;轮印半径r=224 mm。下层地基雪的设计参数参考文献[20], 平均密度ρ=0.48 g·cm-3; 通过计算得到C2为11; 弹性模量E2=44 MPa。

步骤2: 下面假设道面厚度h和弹性模量E1,并计算相应的道面厚度与轮印半径比h/r, 以及上层道面C1, 计算结果见表1 和表2。其中, 轮印半径r=224 mm, 下层雪跑道弹性模量E2=44 MPa。

表1 厚径比Table 1. Thickness-diameter ratio

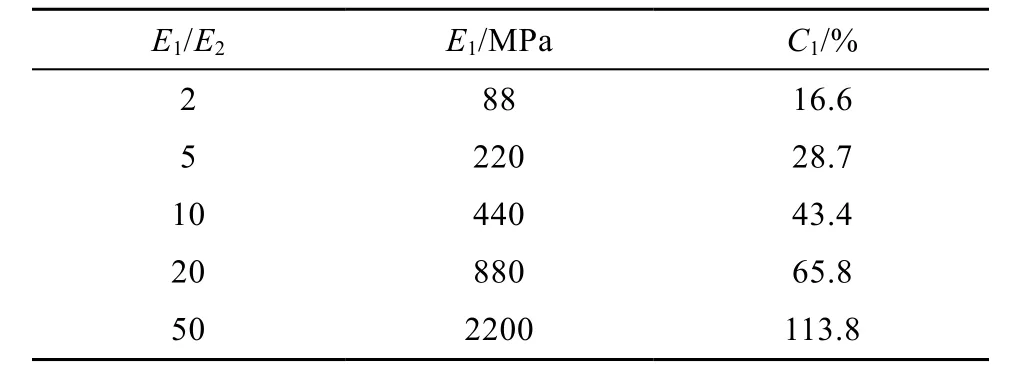
表2 弹性模量比Table 2. Elastic modulus ratio

步骤3: 通过图3 计算不同h和E1/E2下, 道面弯沉影响系数F(表3)。

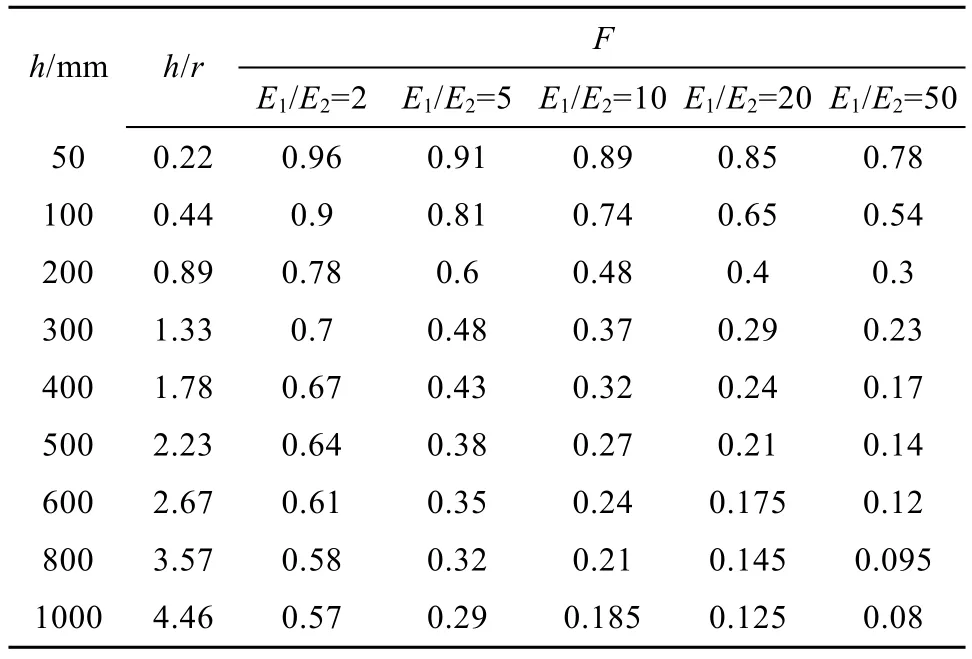
表3 弯沉影响系数计算Table 3. Calculation of settlement influence coefficient

步骤4: 在一定的h和CBR 组合下, 通过公式(7)计算道面弯沉(表4)。

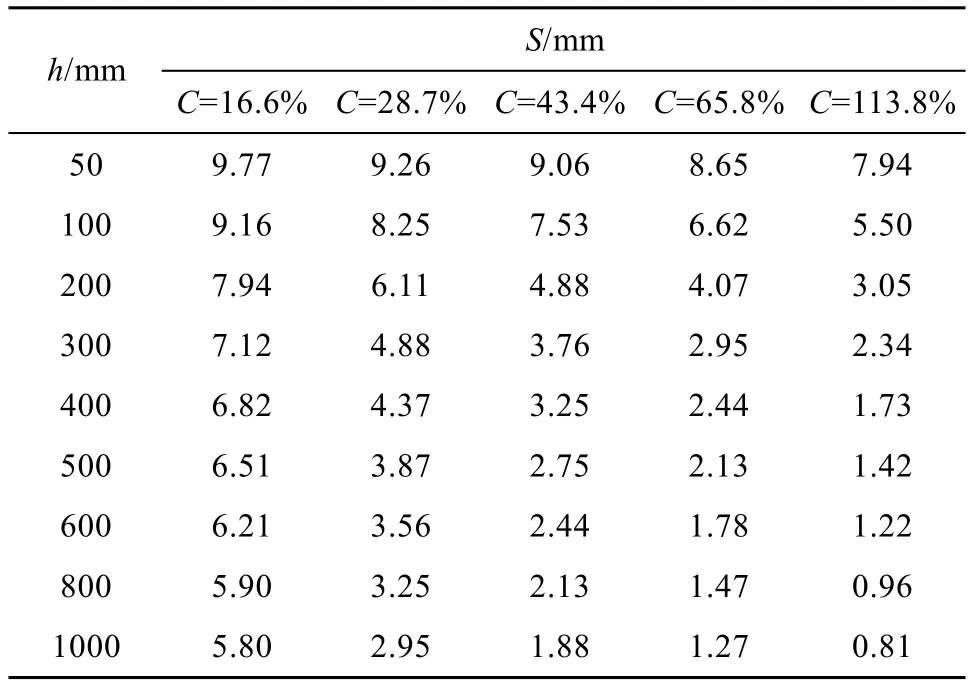
表4 道面弯沉计算Table 4. Settlement calculation of pavement

步骤5: 绘制一定道面CBR 下, 道面弯沉和上层厚度h的关系(图4); 绘制给定一定道面厚度h下, 道面弯沉和上层CBR 关系(图5)。

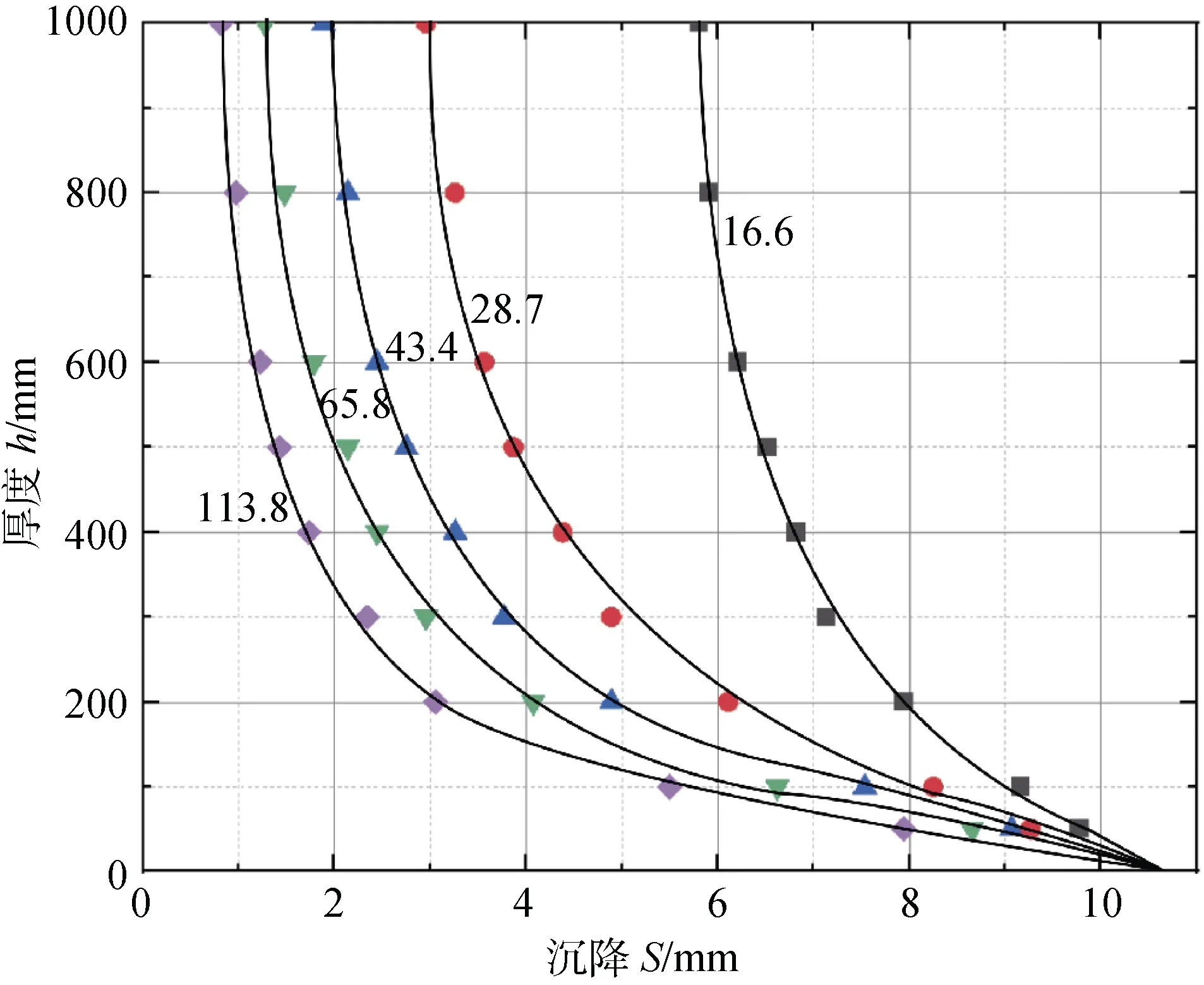
图4 弯沉量与道面厚度关系(CBR 不变)Fig.4. Relationship between settlement and pavement thickness (CBR unchanged)

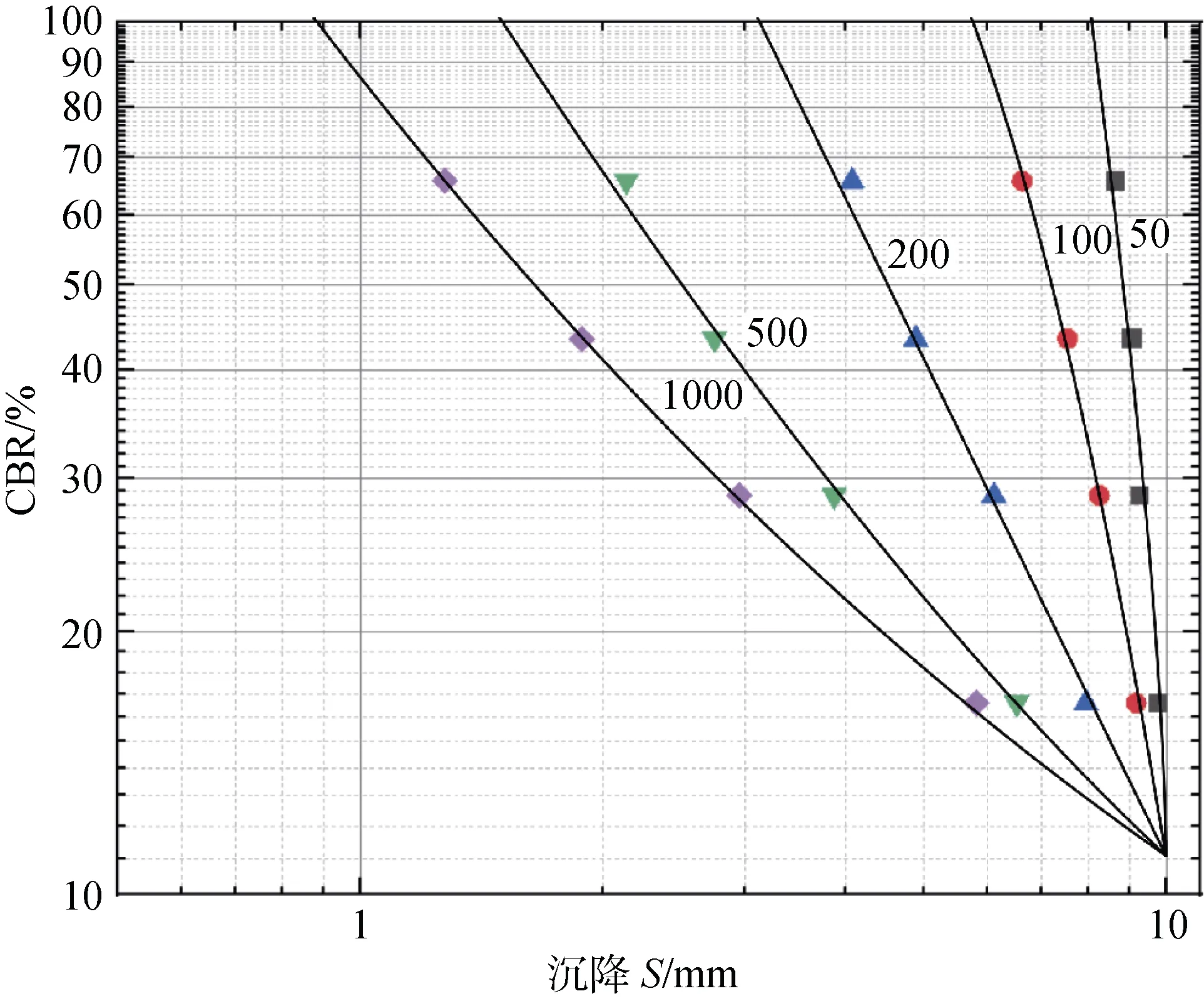
图5 弯沉量与道面CBR 关系(厚度不变)Fig.5. Relationship between settlement and CBR (h unchanged)

步骤6: 通过图4 和图5, 计算一定道面弯沉下, 不同CBR 对应的道面厚度; 计算一定道面弯沉下, 不同道面厚度对应的CBR。具体数据如表5、表6 所示。

表6 不同弯沉标准下CBR 选择Table 6. CBR selection under different settlement standards

步骤7: 基于表5 和表6, 绘制道面指标设计图, 如图6 所示。横轴为道面CBR, 纵轴为道面厚度h。

图6 道面指标设计图Fig.6. Road indicator design

图6 为不同道面弯沉所对应的上层道面厚度h以及上层道面料CBR 值。可以看出, 一定弯沉值对应不同的h和CBR, 设计中可选择高强度低厚度的设计指标或者低强度高厚度的指标。从图6 中可以看出, 弯沉越大, 所需的上层道面厚度和强度越小,S=2 mm 时, 道面设计指标可取C=100,h=370 mm 或者C=41,h=1000 mm。随着弯沉的增加, 道面强度和厚度不断减小,S=8 mm时, 道面设计指标可取C=25,h=100 mm 或者C=12.8,h=1000 mm。由表可知, 在S=10 mm 时,不同道面厚度下, 材料CBR 均为11, 即道面材料强度不变, 且与下层的雪层材料强度一致, 这也是上层道面强度理论上的最低值, 因为跑道设计要求上层的强度不小于下层。对于A320 机型, 在本文雪层地基参数条件下, 最大弯沉为10 mm。

3 实测经验法

3.1 设计依据及思路

实测经验法采用现场实测手段, 将不同荷载组合作用于雪层道面, 并对道面进行现场弯沉测量, 确定弯沉标准, 得到荷载组合作用n次, 满足弯沉设计标准的上层道面设计指标[19]。

该设计方法的目标是得到上层雪道面的强度(用硬度R表征), 且要求目标强度设计的雪层厚度达到轮印半径, 而一般机型的轮印半径在200～300 mm 之间。该方法认为与轮胎直接接触的上层道面强度是胎压、单轮载重和荷载作用次数的函数。故首先建造了不同硬度的雪跑道场地,通过现场试验得到不同胎压和单轮载重组合下,荷载作用一次的道面弯沉。以弯沉10 mm 作为设计标准, 确定胎压和飞机载重组合作用1 次所需的表层硬度R1, 建立R1与胎压P和飞机载重M的关系; 继续对不同胎压和单轮载重组合作用n次的道面弯沉做研究, 在相同弯沉设计标准下,确定作用n次所需硬度Rn。基于此, 建立Rn/R1与荷载作用次数n的关系, 最终得到Rn与胎压p、飞机载重M和作用次数n的关系。

3.2 设计过程

3.2.1 定义有效荷载条件L

首先考虑荷载作用 1 次的情形, 这时有效荷载条件L应为为胎压P和单轮载重M的函数,该指标可以表征荷载水平。下面说明如何确定该函数。

先考虑M对L的影响, 将不同P和M的组合分别作用于不同硬度的雪层道面, 并对道面弯沉S做测量。道面弯沉可分为3 个类型:S≤10 mm,安全; 10 mm＜S≤50 mm, 边界;S＞50 mm, 破坏。将所有安全和边界的组合绘制于图7 中, 发现当胎压P一定时,R1与M呈如图幂函数关系, 其指数约为0.146, 而道面所需硬度又可以反映出荷载的水平, 故可以认为L与M之间也存在该关系。

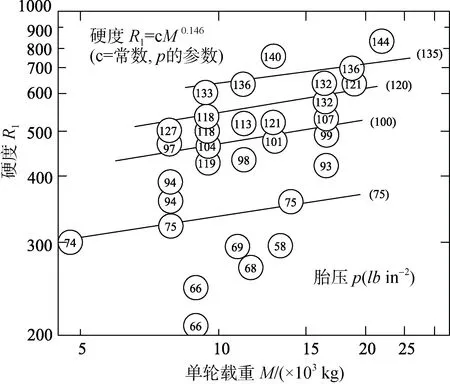
图7 道面硬度与单轮载重关系[19]Fig.7. Relationship between hardness of pavement and single wheel load[19]

再确定L与p的关系。若R1为0, 此时只有p=0时, 对于任何M均有效; 只有M=0 时, 对于任何p也均有效。故L与p和M的关系可以表示为公式(8):

式中,L为有效载荷条件;p为胎压, 单位为kg·cm-2;M为单轮承受飞机重量, 单位为kg。

再结合图7 中不同胎压p下的道面硬度, 可以得到x的值, 最终x近似为1。有效荷载条件L的定义为后续道面硬度推导做准备。

3.2.2 作用1 次道面硬度R1

对于荷载作用1 次的情况, 道面硬度R1可以用L来表示。前文将道面弯沉分为3 个类型, 分别为安全、边界和破坏。将L实测的所有数据绘制于图8, 可以看出, 3 种弯沉类型分别用不同的符号标出。此时取道面弯沉10 mm 作为设计标准,划出强度包络线如图所示。包络线以上为弯沉安全类型, 包络线以下为边界和破坏类型。包络线的数学模型如公式(9)所示:

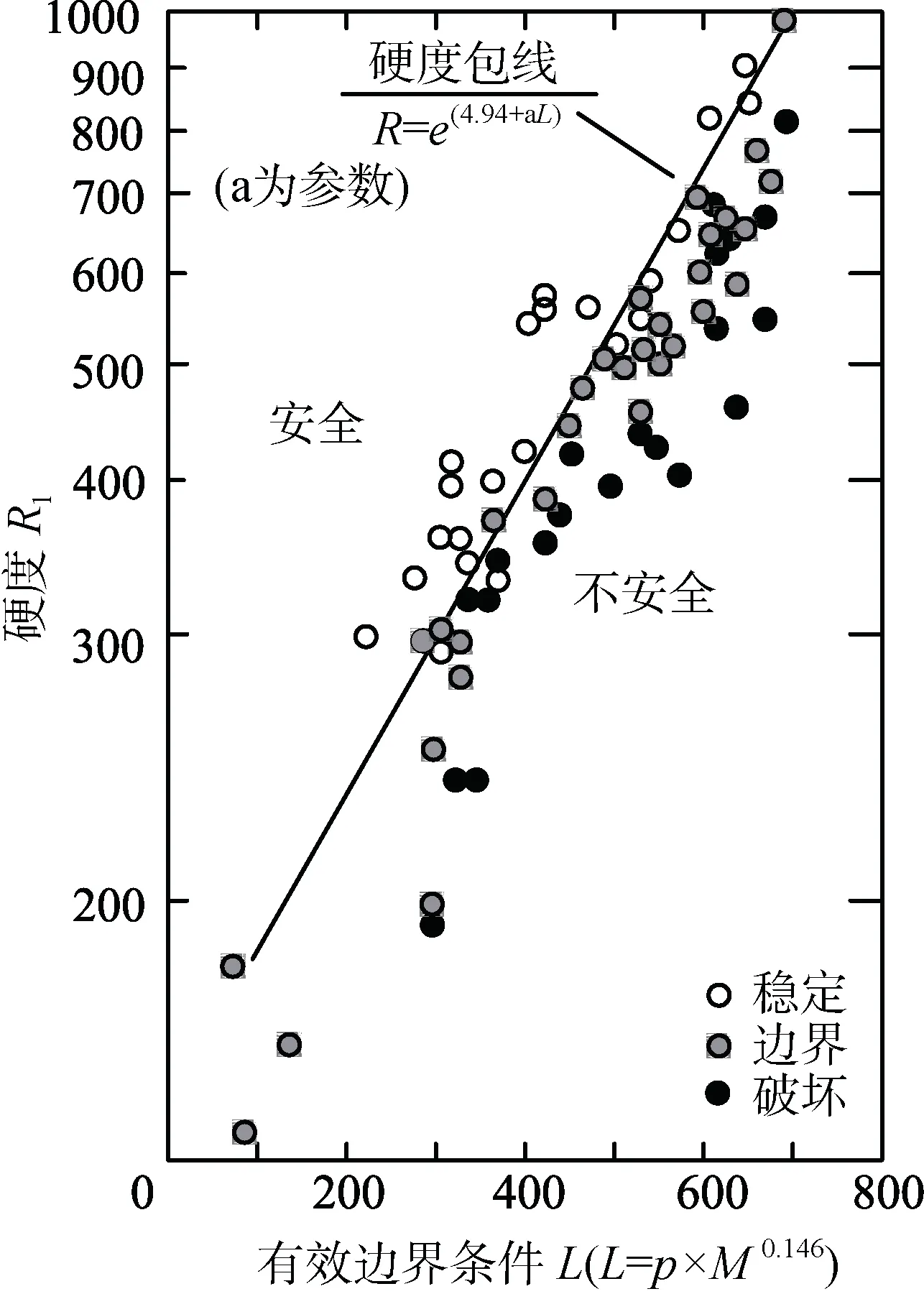
图8 道面硬度与有效荷载条件关系[19]Fig.8. Relationship between hardness of pavement and effective load condition[19]

式中,R1为飞机荷载作用1 次, 达到弯沉设计标准(10 mm)所需的雪层硬度;M为单轮承受重量, 单位为kg; a 为模型参数, 取0.0444。

3.2.3 作用n次道面硬度Rn

在不同硬度的雪层道面上, 施加n次飞机循环荷载, 可参照图8 绘制有效荷载条件作用n次需要的道面硬度Rn。将Rn/R1与作用次数n绘制成图9, 图中各点为不同的荷载组合, 空心代表安全, 实心代表破坏。大体上, 可以用包络线将这些点做划分, 包络线以上为安全, 以下为破坏。包络线可以用公式(10)表示:

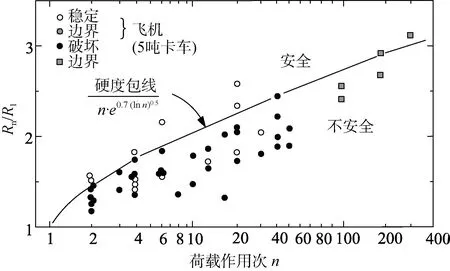
图9 道面硬度比与荷载作用次数关系[19]Fig.9. Relationship between hardness ratio of pavement and loading times[19]

式中,Rn为飞机荷载作用n次, 达到弯沉设计标准所需的雪层硬度;n为飞机荷载作用次数。

该式的物理意义是, 当荷载作用次数为n次时,道面的硬度与荷载单次作用所需硬度的比值。

将公式(10)和公式(9)联立, 可以得到, 当弯沉设计标准为10 mm, 有效荷载条件作用次数为n时, 上层雪道面要求的设计硬度公式(11):

3.2.4 强度设计

前3 步为满足弯沉设计标准的要求, 经验法同时需要满足强度设计的要求。为保证雪在飞机荷载下不发生强度破坏, 采用Boussinesq 公式计算飞机荷载随深度的应力分布, 并保证各深度飞机荷载竖向应力σz小于雪的无侧限抗压强度fu。实际工程中, 道面中的雪处于有侧限状态, 采用无侧限抗压强度设计趋于保守。故实际应用时安全系数不宜过大, 取1.2 比较合适。

式中,σz为飞机荷载在某深度的附加应力(雪的密度按0.5 g·cm-3计算, 1 m 厚的雪竖向应力为5 kPa,远小于胎压, 可忽略), 单位为MPa;fu为该深度雪层的无侧限抗压强度, 单位为MPa。

3.3 设计案例

以空客A320 机型为例, 其最大起飞重量为754.6 kN, 主起落架荷载分配系数为0.931, 主起落架总轮数为4, 故单轮的载荷为175.6 kN, 约17560 kg; 主起落架轮胎压力为 1.14 MPa, 为11.4 kg·cm-2, 一次起降的飞机荷载作用次数为2。

将该机型的参数代入公式, 可以得到R2为1690, 代入公式得到CBR 为51, 无侧限抗压强度为15.99 kg·cm-2, 即1.599 MPa。对道面表层做强度验算, 安全系数取1.2, 可以得到1.2p=1.2×1.14=1.368 MPa, 目标强度满足表层道面抗压要求。

4 两种设计方法的讨论

4.1 实测经验法的进一步讨论

由实测经验法可知, 该方法要求道面上部的目标强度的雪层厚度为轮印半径, 以A320 机型的参数做设计, 取10 mm 作为弯沉设计标准, 2 次作用得到上层道面目标强度为CBR 值51。当改变荷载组合作用次数时, 上层道面的R值将相应改变, 其CBR、fu和雪层密度ρ均有所变化, 表7为不同设计轮载作用次数下所需的上层道面设计指标。

由表7 可以看出, 荷载组合作用1 次道面的硬度R为1151, 作用2 次时为1690, 增加约50%,作用 10 次时增加 100%, 作用 100 次时增加200%。荷载组合作用1、2、4、10、100 及400次时, 所对应的CBR 值分别为42、51、55、59、68 及73。若采用弹性法, 当采用上述CBR, 其道面弯沉均小于10 mm; 而当选取10 mm 为道面弯沉设计标准时, 弹性法计算的道面CBR 明显小于经验法, 因此经验法相比弹性法更加保守。

此外, 经验法对雪层强度也有要求, 其要求道面下各深度的附加应力与雪的强度满足公式(12), 其中σz通过Boussinesq 公式进行求解。图10 为A320 机型引起的附加应力随深度的变化,各深度的强度要满足大于1.2 倍附加应力的要求,故理论上雪层强度也应为曲线。但考虑到实际施工过程中, 各深度强度严格按照曲线来施工过于复杂, 故可将上层道面沿深度分段施工, 每段雪的强度一致, 只要该段最高点满足公式(12), 其他深度自然满足。

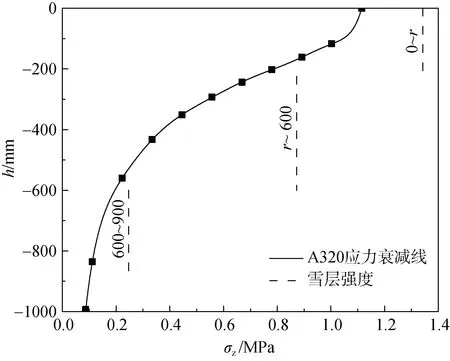
图10 A320 随深度应力衰减曲线Fig.10. A320 stress attenuation curve with depth

图10 中将道面分为3 层进行分析, 设计强度要求如虚线所示。0～r雪层设计强度为1.37 MPa;r～600 mm 为0.87 MPa; 600～900 mm 为0.25 MPa。由于底层地基CBR 值为11, 采用公式(1)和公式(2)得到底层雪地基的无侧限抗压强度为0.255 MPa,下层雪地基的无侧限抗压强度0.255 MPa 大于600～900 mm 深度处的设计强度0.25 MPa, 可将底层地基作为第3 层, 故只需对0～600 mm 雪层进行处理。

4.2 两种设计方法对比

在弹性法的设计过程中, 压实雪路面的设计受飞机类型和场地雪层强度的影响, 弹性法设计可以得出不同标准的弯沉值图, 从而有效防止飞机陷入强度较低的雪中, 适用于已知起落架数量和最大飞机质量的飞机, 需要用到的飞机参数有轮胎压力和轮胎接触面积的半径。但由于南极雪层的CBR 受密度、年龄和温度等因素的影响, 具体跑道参数需要进行具体的现场调查来确定。此外, Burmister 法对非线性塑性变形材料的适用性有待探讨, 由CBR 推导出的压实雪的弹性模量值在较大尺寸的轮印半径和路面上可能不准确, 并且雪层的泊松比也不容易测量。

经验法需要用到的参数有飞机轮胎胎压、飞机轮载和飞机车轮荷载作用次数。在南极雪层跑道上进行的飞机起降试验证明了这种设计标准的有效性和安全性。Wuori[23]认为高密度雪中可以通过使用Boussinesq 方程来近似描述应力分布,但Boussinesq 方程在雪中的适用性尚未在实验中得到充分研究。此外, 该方法未考虑快速移动载荷对雪路面的动态效应, 且设计弯沉值标准也无法改变。

下面对比该机型的设计结果, 实测经验法取10 mm 作为弯沉设计标准, 2 次作用得到上层道面目标强度为CBR 值51。弹性双层体系法中, 由图6 可以看出, 当CBR 值为51, 道面厚度为轮印半径224 mm 时, 该点落在弯沉4 mm 线上, 弯沉值低于经验法。若两种方法的弯沉标准统一, 弹性法的道面强度将低于经验法。

综合对比两种设计方法(表8), 可以看出, 经验法设计过程中不仅考虑了胎压和轮印半径, 还考虑了轮载和作用次数; 设计中既要满足道面弯沉, 还要满足雪层强度要求; 从设计指标上看,经验法的道面指标比弹性法更加安全。因此, 经验法较弹性法更加科学和安全。

表8 两种设计方法对比Table 8. Comparison of two design methods

5 结论

本文总结了国外两种压实雪层跑道设计方法,并以空客A320 机型为例, 进行了雪跑道设计及其方案对比, 得出以下结论。

1. 双层弹性体系法以上层道面厚度h和CBR 为目标设计指标。针对不同厚度和弹性模量组合, 利用Burmister 理论求解道面弯沉, 可得到不同弯沉标准下道面厚度h与CBR 组合。其优点在于设计理论成熟, 可基于不同的弯沉设计标准选择道面指标, 并根据环境温度确定雪层密度(通过CBR 换算); 其局限在于仅考虑了胎压, 未考虑单轮载重和荷载组合作用次数, 且未做强度验算设计。

2. 实测经验法以上层道面硬度R为目标设计指标。针对不同胎压和单轮载重进行现场试验,对荷载组合作用后的道面弯沉做测量, 选取10 mm 为设计标准, 确定上层雪道面的硬度R。其优点在于经过现场实测的数据更有说服力, 设计方法同时考虑了胎压、单轮载重和作用次数,同时对各深度雪的强度做了验算; 其局限在于弯沉设计标准为10 mm, 不能根据机型做出变化,且对于荷载组合高作用次数的情况不适用。

3. 以空客A320 机型为例, 利用两种设计方法对压实雪层跑道做了对比。经验法设计过程中考虑的因素更加全面, 设计中要求满足道面弯沉和强度两种标准, 相同弯沉标准下, 经验法得到的道面强度要高于弹性法。故与弹性法相比, 实测经验法更科学和安全。

本文的对比是基于A320 机型参数以及文献[20]中冰雪层性质进行的设计, 针对不同机型和冰雪层的道面设计有待进一步研究。此外, 两种方法对于设计指标的单位要求不完全相同, 这在设计中需要重点关注。