飞机主电源系统关键器件健康状态评估研究
李小宁 高朝晖 王 爽 汤 孝 李一卓
(1.西北工业大学自动化学院 西安 710129;2.中国商飞上海飞机设计研究院 上海 201210;3.中航长沙设计研究院有限公司 长沙 410014)
1 引言
飞机主电源系统担负着为全机供电的任务,其正常工作对于飞行安全和飞行任务的完成至关重要[1],一旦主电源系统发生故障,将直接影响飞机正常飞行,甚至造成严重事故。基于飞机主电源系统外部特征数据,对系统的健康状态进行评估,可以实现飞机主电源系统潜隐故障和早期故障的预警,有助于增加飞机的安全可靠性、降低维护成本、提高飞机整体的信息化和智能化水平,具有重大意义。飞机主电源系统部件繁多、结构复杂,一般而言,其内部机械结构较为稳定可靠,而其内部电路则故障率高发,主要是因内部电路中包含大量电力电子器件且半导体器件抗干扰、抗过载能力较差所致[2-5]。
目前对于复杂系统的故障特征提取和健康状态评估常采用数据驱动(Data-driven)和数据挖掘相结合的方法实现[6-7]。文献[8-10]分别采用基于灰色关联度(Grey relation analysis,GRA)、基于深度置信网络(Deep belief network,DBN)和基于宽度学习系统(Broad learning system,BLS)的特征自适应提取方法对航空三级发电机中旋转整流器的二极管进行故障特征提取和诊断;文献[11]利用数据采集与监视控制系统(Supervisory control and data acquisition,SCADA)提出了基于高斯混合模型(Gaussian mixture model,GMM)的风电机组发电机健康状况的评估方法;文献[12]采用基于期望最大(Expectationmaximization,EM)与高斯混合模型相结合的算法对火电厂发电设备进行故障模式识别和智能诊断预测。
当前在飞机研制过程中,由于主电源系统健康状态评估的研发还处于起步阶段,系统中现有的监测信号是否可以满足状态评估的需要、是否需要另行加装传感器进行相关特征数据的采集、如何通过有限的监测信号进行数据解耦从而准确判定出监测对象的健康状态等问题有待解决。针对以上问题,本文展开飞机主电源系统关键器件健康状态评估方法研究,建立了飞机主电源系统仿真模型,通过蒙特卡罗分析,获取大量仿真数据,确定出飞机主电源系统中励磁机励磁电压和励磁电流平均值作为系统外部特征变量,来进行系统状态评估;采用主成分分析(Principal component analysis,PCA)方法对系统关键器件同时老化时所监测到的外部特征变量数据进行解耦,用解耦后的数据建立高斯混合模型,计算系统老化模型和健康基准模型间的马氏距离,并通过聚类分析,对系统健康状态等级进行判断;采用BP(Back propagation)神经网络最终实现对飞机主电源系统关键器件健康状态的评估。
2 飞机主电源系统关键器件的老化特性
2.1 飞机主电源系统关键器件的确定
飞机主电源系统包含大量部件,各部件的工作环境和使用寿命不同。对于系统的健康状态评估,如果将主电源系统所包含的全部部件作为监测对象,在效率和效果两个方面都是不理想的,因此进行飞机主电源系统的健康状态监测需要合理选择监测对象。当前,飞机主电源系统通常由飞机发电机及其控制与保护设备构成,飞机发电机常采用三级式无刷交流发电机,三级发电机包括永磁副励磁机、交流励磁机、旋转整流器和主发电机[1]。飞机主电源系统结构如图1 所示。
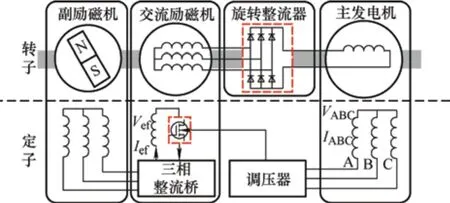
图1 飞机主电源系统结构图
一般而言,飞机主电源系统中半导体器件相较于机械结构更容易出现故障。经过充分调研,根据部件发生故障频率和发生故障后对系统的危害程度等因素,选择调压器中的MOSFET 开关管和旋转整流器的功率二极管作为导致飞机主电源系统老化的内部关键器件,加以重点监测。关键器件在图1 中用虚线线框标出。其中,调压器中的MOS 管,承担着保证主电源能否输出正常电压的关键任务;旋转整流器的功率二极管,工作时处于高温和高速旋转状态。两者的工作环境都较为恶劣,在热应力、电应力和力学应力等多重因素作用下容易老化,故障率高,故障后对系统影响较大。
2.2 调压器中的功率MOS 管
调压器中的MOS 管主要在热循环应力下逐渐老化[13]。美国NASA 的研究人员CELAYA 等[14-15]针对功率VD-MOS 开关管(IRF520Npbf)分别进行了长时间热应力和热循环应力加速老化试验,该试验在MOS 管的开关工作过程中监测了漏电流、漏源电压、栅极电压、封装温度等外部参数,分析了这些外部参数的变化趋势,发现老化过程中功率MOS管导通电阻的增加最为明显,该阻值会随着器件工作时间增加而上升,直至突然失效。本文研究的飞机主电源容量为60 kV·A,将主电源调压器中采用的功率MOS管参数和参考文献[15]中的数据结果进行类比分析,最终确定本文主电源中采用的功率MOS 管从完好至老化状态,其导通电阻的变化范围为0.3~2.7 Ω。
2.3 旋转整流器中的整流二极管
高温和高速旋转状态使得旋转整流器中的功率二极管在多重应力作用下容易老化,故障率高发。文献[16]针对结势垒肖特基二极管进行了正向大电流应力条件下的老化试验,发现每组被测二极管的正向电压随着器件老化呈现出增大的趋势;文献[17]中,YOSHIDA 等针对以TiN 为接触面的PN 结二极管进行了反向偏置电压高温应力试验,结果显示反向漏电流会随着老化时间呈现上升趋势。基于上述研究,本文选定正向电压和反向漏电流作为反映整流二极管老化的参数。
本文中为了研究60 kV·A 飞机主电源中整流二极管的老化特性,搭建了二极管热循环加速老化试验台,对二极管进行老化试验。二极管在不加散热片的状态下通以额定电流,测量二极管外壳温度,温度上升至120 ℃,断开电流,壳温下降至40 ℃时恢复通电。每20 次循环为一个周期,每个周期结束测量一次二极管导通压降和反向漏电流,如此往复,直至二极管损坏。试验结果表明,所测试整流二极管的正向电压和反向漏电流随老化时间呈现增大的趋势,并最终确定所测二极管从完好至老化状态,正向电压和反向漏电流的变化范围分别为1.6~3.6 V 和0~200 μA。
3 系统外部特征变量的选取
3.1 系统外部特征变量的选择及变化规律
由于直接获取三级发电机转子上的信号较为困难,因此只能对飞机主电源系统外部可测量的变量进行数据采集分析,来对系统进行状态评估。可测量的系统外部特征变量主要分为两类:主发电机电枢端输出的三相电压电流和交流励磁机励磁绕组端输入的电压电流。
可选的外部特征变量如下:① 主发电机输出三相电压有效值VABC;② 主发电机输出三相电流有效值IABC;③ 主发电机单相输出电压交流畸变系数dfVABC;④ 主发电机单相输出电流交流畸变系数dfIABC;⑤ 励磁机的励磁电压平均值Vef;⑥ 励磁机的励磁电流平均值Ief;⑦ 励磁机的励磁电压直流畸变系数 dfVef;⑧ 励磁机的励磁电流直流畸变系数 dfIef。
在本文中,采用Saber 软件建立飞机主电源系统蒙特卡罗仿真模型,来选择表征系统内部关键器件老化的外部特征变量。
在蒙特卡罗仿真模型中,设置飞机主电源系统处于满载,功率因数为0.75,阻感线性负载工况。分别对整流二极管和功率MOS 管进行老化设置,监测系统外部特征变量的变化。仿真模型中设置整流二极管正向电压和反向漏电流同时老化,老化参数符合均匀分布;功率MOS 管的导通电阻也符合均匀分布。在Saber 软件中,均匀分布采用“uniform(a,b)”的形式进行设置,其中参数a为分布的中心值,b为变化比率[18]。由此确定每一阶段老化参数范围为(a-ab,a+ab),在这个范围内所有值出现的概率相同,以此模拟整流二极管在某一阶段的老化状态。根据第2.3 节的说明,从二极管完好到老化,将参数分为4 个等级,其中正向电压VF 中心值分别为1.8 V、2.4 V、2.9 V、3.4 V,反向漏电流IR 中心值分别为25 μA、75 μA、125μA、175 μA,在每个参数等级中设置仿真次数为20,详细的参数设置如表1 所示。表1 省略了关键字,将“uniform(a,b)”简化为“(a,b)”的形式。
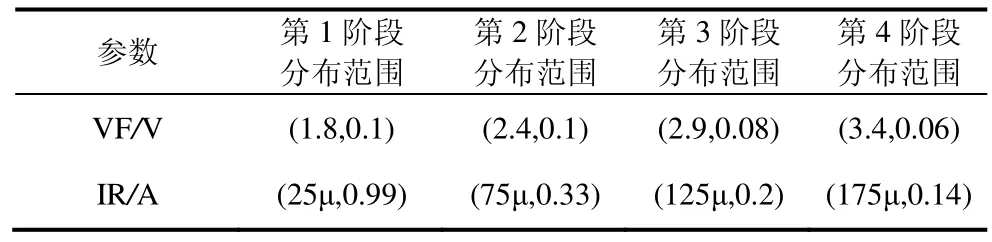
表1 整流二极管的正向电压和反向漏电流设置
经过4 个老化阶段80 次蒙特卡罗仿真后,得到大量主电源系统外部特征参数数据。结果表明,由于调压器的调节作用,在整流二极管的老化过程中,发电机的输出电压、电流等参数的变化不明显;而励磁机的输入励磁电压、励磁电流的平均值和直流畸变系数的变化与整流二极管的老化密切相关。图2 给出了励磁机的输入励磁电压、励磁电流平均值和直流畸变系数在二极管不同老化阶段的数据箱形图,显示二极管处于不同老化阶段,特征变量的均值点、上下限和异常值。可以看出随着整流二极管的老化,励磁机的输入励磁电压、励磁电流的平均值增加,励磁机的输入励磁电压、励磁电流的直流畸变系数减小。
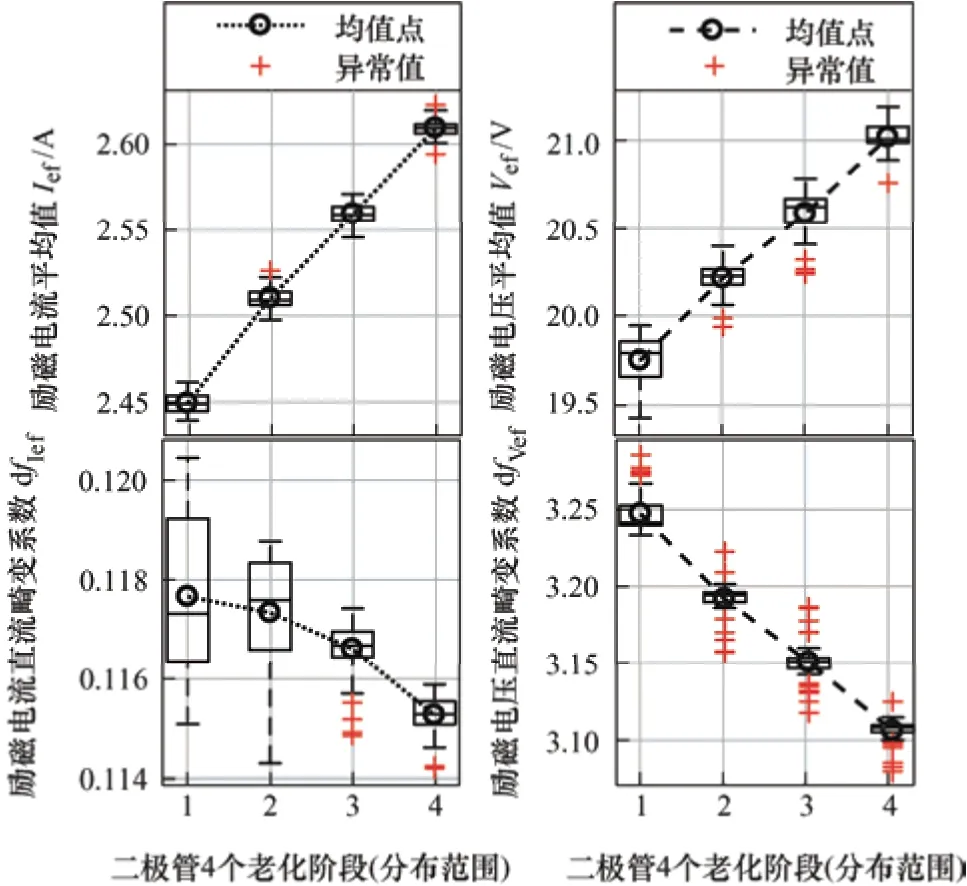
图2 励磁电压电流稳态外特性参数均值曲线和箱形图
本文采用Pearson 相关性分析来剔除图2 所示特征变量中的冗余参数。由于励磁电流平均值的分布最为集中且变化明显,所以采用励磁电流平均值为基准,分析其和其他三个参数在二极管不同老化阶段的Pearson 相关系数。最终确定Pearson 相关系数最小的励磁电流平均值Ief和励磁电压平均值Vef作为表征飞机主电源系统老化的外部特征变量。对MOS 管老化过程进行蒙特卡罗仿真分析也得到相同的结论。
3.2 励磁机输入特征参数随二极管老化变化规律的试验验证
本文采用3 kV·A 发电机试验台对第3.1 节提出的“随着整流二极管的老化,励磁机的输入励磁电压、励磁电流的平均值增加,励磁机的输入励磁电压、励磁电流的直流畸变系数减小”观点进行试验验证。发电机试验台由原动机和发电机组成(图3a),位于发电机右侧的旋转整流器如图3b 所示,其中旋转整流器二极管可串入相应电阻来模拟二极管老化时正向电压增大的现象。

图3 发电机试验台及旋转整流器实物图
分别在旋转整流器二极管正常、串入0.5 Ω 电阻和串入1.5 Ω 电阻时进行试验,三次试验均调节输出电压一致,采集励磁机励磁电流、励磁电压进行分析。励磁机输入励磁电流、励磁电压波形及其平均值如图4 所示。

图4 励磁电流、励磁电压随二极管老化波形及平均值
由图4 可以看出随着二极管的老化,励磁机输入励磁电流平均值Ief、励磁电压平均值Vef增加。通过对图4 中二极管各老化阶段励磁电流、励磁电压进行快速傅里叶分析得出励磁电流直流畸变系数dfIef如表2 所示。由表2 可知,随着整流二极管的老化,励磁机的输入励磁电压、励磁电流的平均值增加,励磁机的输入励磁电压、励磁电流的直流畸变系数减小。
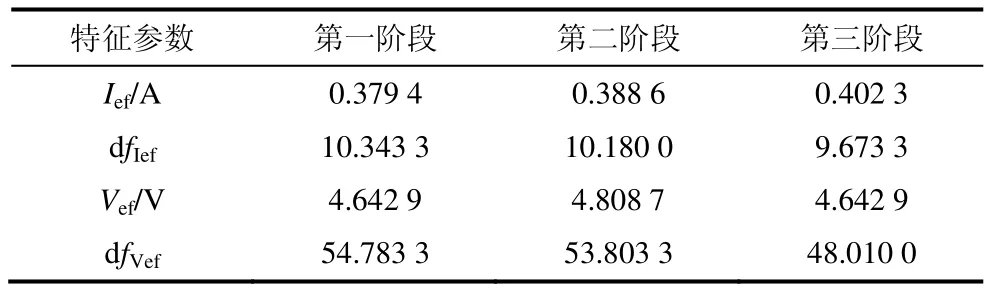
表2 励磁机输入特征参数
3.3 主电源系统工况对系统外部特征变量的影响
引起系统外部特征变量变化的因素不仅是系统内部关键器件的老化,系统工况的变化同样也会引起输入励磁电压和励磁电流的变化。为了排除工况对系统外部特征变量的影响,从而避免对系统健康状态的误判,本文就工况对系统外部特征变量的影响也进行了分析。
为了飞机的安全性考虑,必须使电源有一定的安全裕量,因此在主电源仿真模型中设置除过载以外的不同工况如下所示。
(1) 线性阻感负载下,系统输出视在功率分别为系统额定功率的10%、50%和100%。
(2) 满载情况下,系统输出功率因数分别为1.00、0.75、0.50 和0.30。
(3) 满载情况下,系统输出功率因数设为0.75,系统输出电流畸变分别为<0.01%、3.85%、17.8%、29.5%、45.8%。
在以上工况下,测试主电源系统外部特征变量的变化,可得如下结论[19]。
(1) 励磁机励磁电压和励磁电流平均值随着系统输出视在功率的增加而增加。
(2) 励磁机励磁电压和励磁电流平均值随着系统功率因数的增加而减小。
(3) 励磁机励磁电压和励磁电流平均值随着输出电流交流畸变系数的增大而减小。
由上述分析可以看出,飞机主电源系统的工况会对系统外部特征变量产生影响,所以在对系统进行健康状态评估时,必须对监测到的数据进行系统工况的甄别。本文选择最典型的工况来进行系统健康状态评估,即满载(60 kV·A)、功率因数0.75、线性阻感负载。
4 系统外部特征变量数据的获取及解耦
4.1 系统外部特征变量数据的获取
在飞机主电源蒙特卡罗仿真模型中,设置旋转整流器中6 个整流二极管正向电压和反向漏电流,以及调压器中的功率MOS 管的导通电阻都服从均匀分布,对于整流二极管的正向电压和反向漏电流,以及功率MOS 管的导通电阻,从器件完好到老化,与前类似,同样设置了四个阶段。其中整流二极管的正向电压和反向漏电流同时老化:正向电压范围(1.62,1.78)即uniform(1.8,0.1)和反向漏电流范围(0.25μ,49.75μ)即 uniform(25μ,0.99)代表二极管处于优的状态,正向电压范围(2.16,2.64)即uniform(2.4,0.1)和反向漏电流范围(50.25μ,99.75μ)即uniform(75μ,0.33)代表二极管处于良的状态;MOS 管导通电阻范围(0.3,0.9)即uniform(0.6,0.5)代表MOS 管处于优的状态,MOS 管导通电阻范围(0.9,1.5)即uniform(1.2,0.25)代表MOS 管处于良的状态。状态中和差的仿真组设置同优、良状态类似。参数的具体赋值如表3 所示。表3 中省略了关键字,将“uniform(a,b)”简化为“(a,b)”的形式。
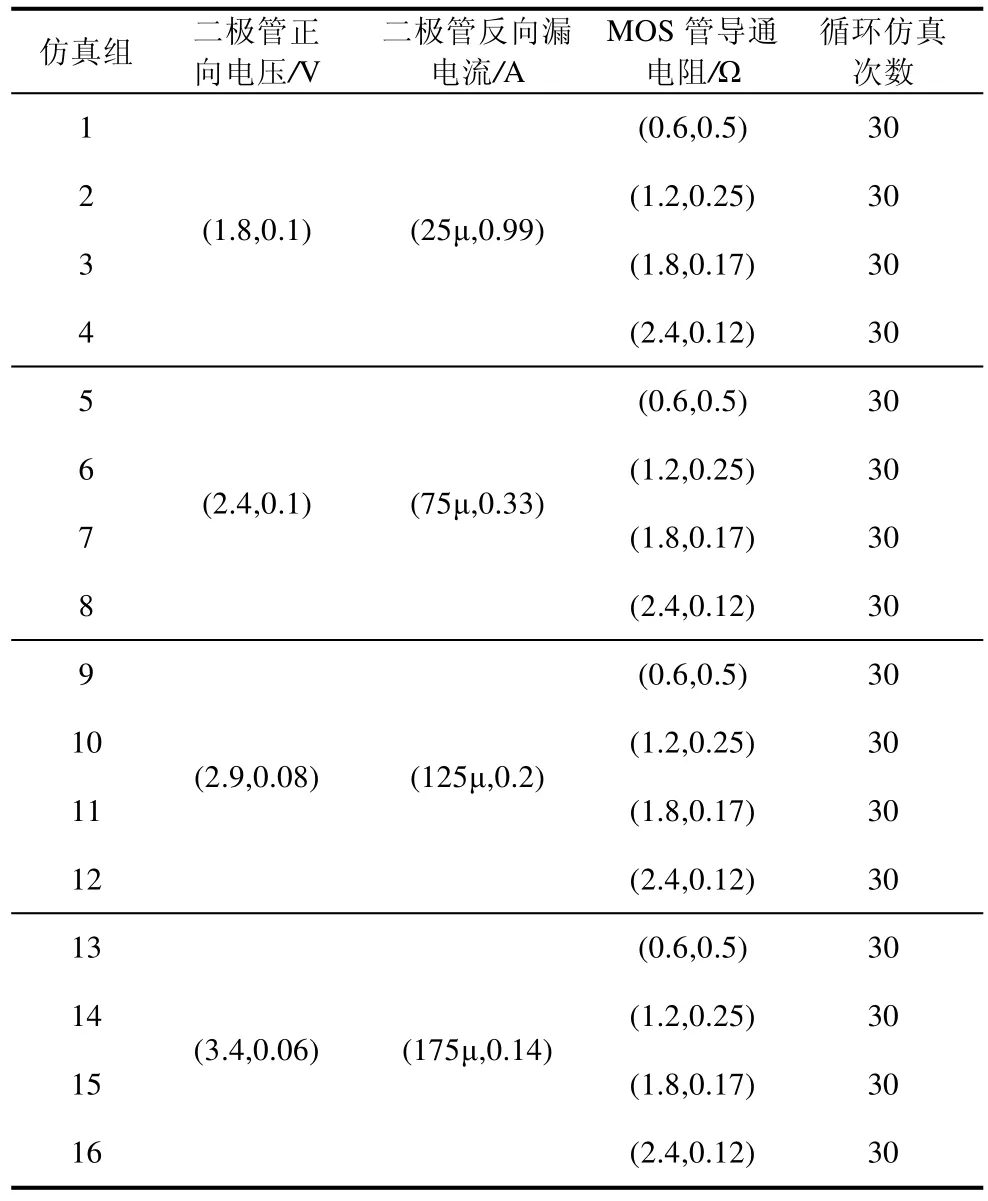
表3 蒙特卡罗仿真组中关键器件参数分布设置
一共进行了16 组蒙特卡罗仿真,每组循环仿真次数设置为30 次。可以看出,表3 中第1、2、3、4 组仿真代表整流二极管处于完好状态、功率MOS管单独老化的过程;第1、5、9、13 组仿真代表功率MOS 管处于完好状态、整流二极管单独老化的过程;其余各组数据代表功率MOS 管和整流二极管同时处于不同老化阶段。通过16 组蒙特卡罗仿真分析,可以获取系统不同健康状态下的系统外部特征变量数据。
图5 所示为表3 中第1、2、3、4、5、9、13组蒙特卡罗仿真产生的系统外部特征变量数据。图5 纵坐标为电压平均值Vef,横坐标为励磁电流平均值Ief。从图5 可以看出,功率MOS 管单独老化导致的系统外部特征变量Vef和Ief的变化范围较小,在图6 中,对MOS 管单独老化时获取的第1、2、3、4 组数据进行了局部放大。从图5 和图6 可以看出,不同仿真组的Vef和Ief之间的斜率k均约为8.091,接近励磁机励磁绕组的电阻值(8.06 Ω)。
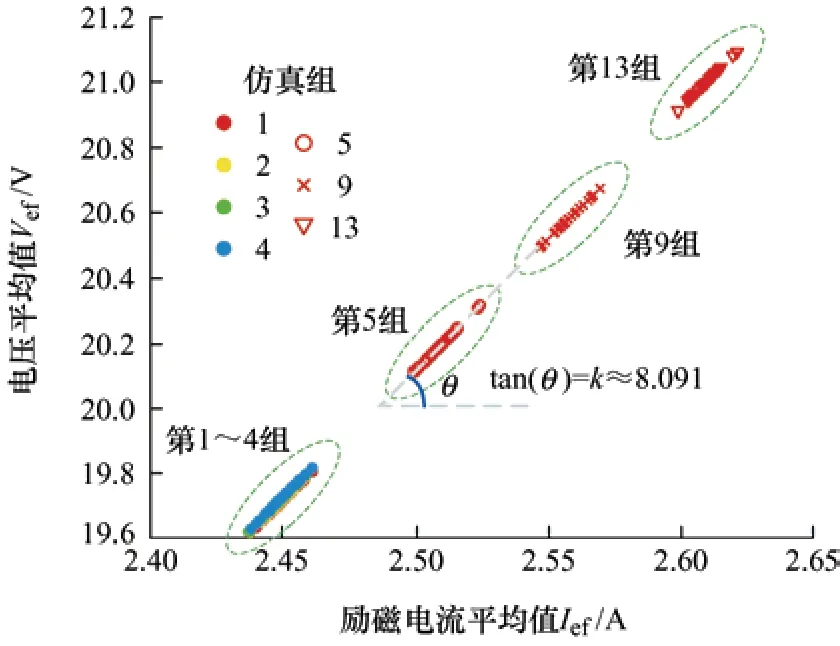
图5 特征变量数据分布情况

图6 部分特征变量数据局部放大
由于图5 和图6 所示的数据存在功率MOS 管和整流二极管不同老化阶段引起的系统外部特征参数的相互耦合,且两种器件引起的外部特征变量变化范围相差较大,因此直接根据图中的数据很难判断出功率MOS 管和整流二极管各自的老化程度。接下来,本文将利用主成分分析的方法对整流二极管和功率MOS 管老化过程中获取的数据进行解耦。
4.2 飞机主电源系统老化数据的解耦
观察图5 可以看出,Vef和Ief在斜率为k的直线方向上分布差异较大,即在该方向上老化数据的方差较大。从概率统计的观点来看,随机变量的方差代表了其含有的信息,方差值越大表示该变量包含的信息就越多[20]。
主成分分析通过线性变换将原始数据变换为一组各维度线性无关的数据,其基本原理就在于用一组综合变量去替代多个随机变量,尽量少丢失随机变量所携带的信息,并且使综合变量彼此之间互不相关[21-22]。从几何的观点来看,主成分分析是对数据原坐标轴进行一个坐标旋转,得到相互正交的新坐标轴,新坐标轴的方向为数据点方差最大的方向[20]。本文利用主成分分析法对系统外部特征变量Vef和Ief进行解耦。
将表3 中第1、2、3、4、5、9、13 组共210次仿真得到的老化数据Ief和Vef按每次仿真的数据作为一列组成矩阵,矩阵A0为2 行210 列。
主成分分析主要包括以下计算步骤[23]。
第一步:将原始数据进行零均值处理。先计算矩阵A0中每一行的均值,然后将矩阵A0中每个元素都减去所在行的均值,得到矩阵A,使得矩阵A中每行数据的均值为0。
第二步:计算矩阵A的协方差矩阵C。由于矩阵A的每行数据均值为0,因此协方差矩阵C的计算如式(1)所示
协方差矩阵C中对角线元素的值是矩阵A中每行数据的方差;非对角线元素的值是矩阵A中不同行数据间的协方差。
第三步:计算线性变换矩阵P,使得PCPT运算的结果满足协方差矩阵的对角化,即PCPT矩阵中,对角线元素为协方差矩阵C的特征值,且从大到小依次排列;非对角线元素的值为0。这样变换后的数据矩阵PCPT中,不同行数据间的协方差为0。变换矩阵P的具体求法是计算出协方差矩阵C的特征值和特征向量,将特征值从大到小排列,选取对应的特征向量按行组成线性变换矩阵P。
第四步:计算变换后的数据。将第三步中得到的线性变换矩阵P左乘原始数据矩阵A0即可得到解耦后的数据矩阵B′,数据变换过程如式(2)所示
图7a 给出了矩阵B′中参数CP′D和CP′M的分布情况,图中用不同的线型区分不同的仿真组。从图7a 可见,横向分布的四个数据集(第1、5、9、13组)代表整流二极管的四个老化阶段,整流二极管的老化使得参数CP′D增大,而CP′M基本不变;纵向分布的四个圆点数据集(第1、2、3、4 组)代表功率MOS 管的四个老化阶段,功率MOS 管的老化使得参数CP′M增大,而CP′D基本不变。经过上述变换,成功将由于二极管和MOS 管老化引起的系统特征变量励磁电压和励磁电流平均值的变化进行了解耦,CP′D和CP′M可以分别来表征两种器件的老化程度,进而反映旋转整流器和调压器的老化程度。

图7 解耦坐标系中的老化数据分布
观察图7a 中数据发现,第1 组数据的中心点不在原点,给后续分析带来不便。为了使得该中心点位于原点,对矩阵B′进行坐标平移操作。将矩阵B′中所有数据的横、纵坐标分别减去B′中第一组数据的横坐标均值和纵坐标均值,得到矩阵CPD和CPM为最终解耦后的老化数据。矩阵B中数据的分布如图7b 所示。可以看出,坐标平移前后数据的分布规律是一致的,坐标平移后第1 组数据的中心点位于原点。
5 主电源系统关键器件健康状态评估
5.1 健康基准模型和马氏距离
得到解耦后的老化数据后,将表3 中第1 组蒙特卡罗仿真对应的30 个数据点作为飞机主电源系统“健康”状态的样本集建立高斯混合模型。高斯混合模型理论上可以拟合出任意类型的分布[24],因此利用该“健康”状态的样本集分别建立旋转整流器中整流二极管和调压器中MOS 管的高斯混合模型,并将这两个高斯混合模型作为两个关键器件的健康基准模型。
高斯混合模型由多个高斯概率密度分布P互相线性叠加[25]。如果样本数据是由K个高斯分布P组成,对于样本数据集x= {x1,x2, ⋅⋅⋅,xN}中N个数据中每个数据点xi来说,高斯混合模型的概率密度函数为
式中,αn表示第n个高斯分布在高斯混合模型中所占的权重;Θ为各混合成分的参数向量(θ1,θ2, ⋅⋅⋅,θn, ⋅⋅⋅,θK),其中θn为第n个高斯分布(μn,Σn),μn为第n个高斯分布的期望值,Σn为第n个高斯分布的方差。
高斯混合模型中高斯分布P的个数K的取值需要合理选择,避免出现过拟合和欠拟合的问题。可以采用两种方来确定K值:一种是通过重新生成一组测试集,根据测试集似然函数的变化趋势确定K的取值[26];也可以通过赤池信息量准则中的AIC值确定K的取值,选择AIC最小所对应的K值即可[27]。本文采用这两种方法得到了相同的K值:整流二极管健康基准模型K值为1,功率MOS 管健康基准模型K值为2。在K值已确定的基础上,在Matlab 中通过函数命令“fitgmdist”利用期望最大算法可以拟合出最佳的参数向量Θ。利用表2 中第1 组数据在解耦坐标系中的CPD和CPM分别拟合得到整流二极管和功率MOS 管的健康基准模型,两个健康基准模型的概率分布密度函数如图8 所示。
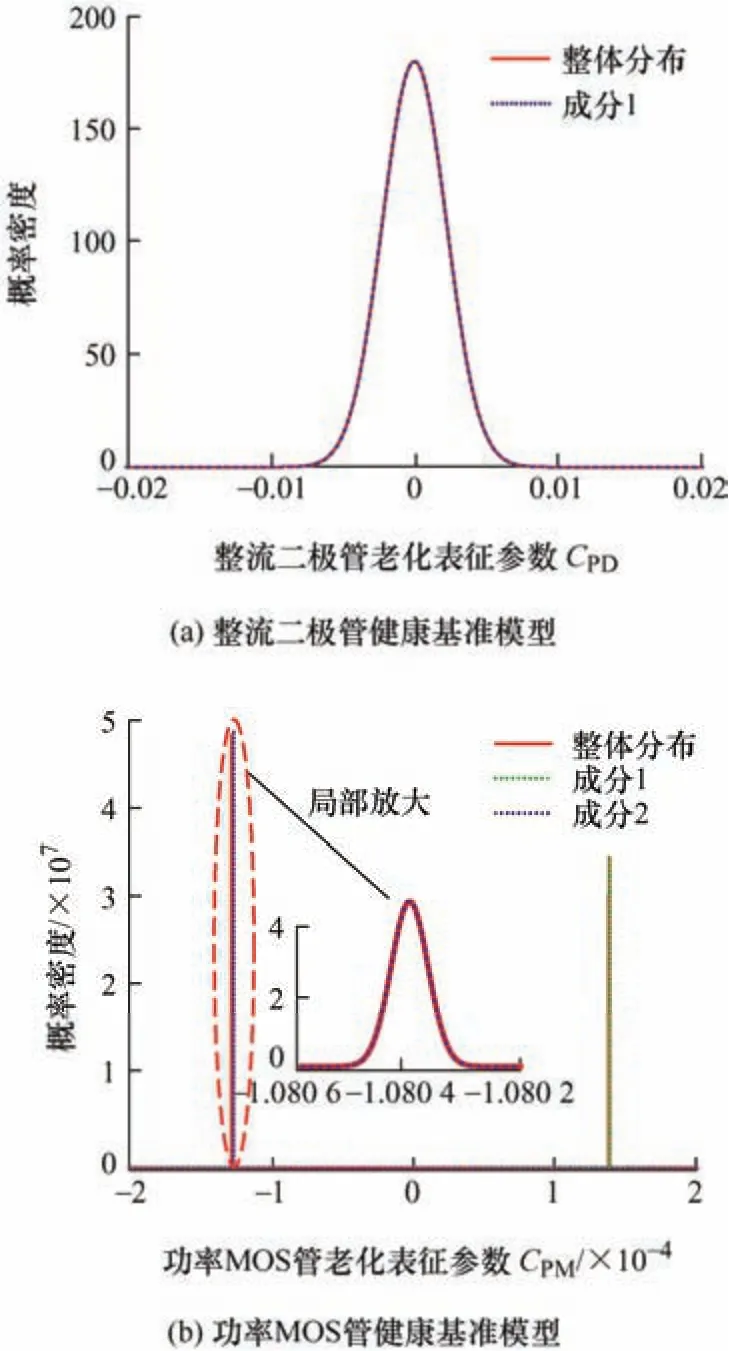
图8 两个关键器件的健康基准模型的概率分布密度函数
为了确定系统关键器件的健康状态,本文计算表3 中第1、5、9、13 组数据解耦后与整流二极管健康基准模型的马氏距离,第1、2、3、4 组数据解耦后与功率MOS 管健康基准模型的马氏距离。马氏距离的计算公式如下[28]
式中,x表示度量空间中的数据点;μ表示高斯分布中各个数据点的期望值;Σ表示高斯分布中数据点之间的协方差矩阵。
对于包含有K个高斯分布的高斯混合模型而言,其与数据点x的马氏距离MD(x)可由式(5)计算[11]
式中,d n(x)为数据点x与第n个高斯分布Pn之间的马氏距离;αn为第n个高斯分布在高斯混合模型中所占的权重αn在Matlab 的“fitgmdist”函数中得到。图9 为计算出的表3 中第1、5、9、13 组数据解耦后与整流二极管基准模型和第1、2、3、4 组数据解耦后与功率MOS 管健康基准模型的马氏距离结果。
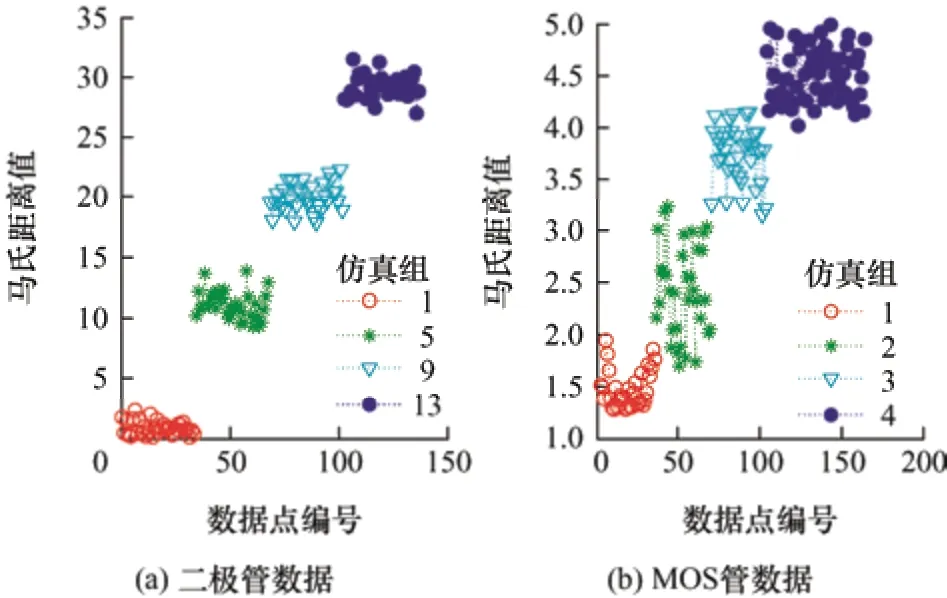
图9 数据样本与两个健康基准模型的马氏距离
在图9a 中,按第1、5、9、13 组数据与整流二极管基准模型计算的马氏距离被清晰地标识为4 个数据集,且与仿真组原始数据设置相一致;但在图9b 中,按第1、2、3、4 组数据与功率MOS 管基准模型计算的马氏距离则不能被清晰地划分,在图中按仿真组原始数据划分的4 个数据集之间的马氏距离存在重合点,因此不能按照原始仿真组数据进行健康状态等级的划分。究其原因,主要是因为MOS管老化对电源系统外特性影响较二极管老化对其的影响小,使得外特性数据励磁电压和励磁电流平均值变化范围小,数据点分布比较集中。因此本文采用聚类分析的方法,以期将图9 中计算的马氏距离数据清晰地划分为4 个互不重叠的“簇”。
5.2 关键器件健康状态等级分类
针对上述按照表3 中原始数据解耦后计算的马氏距离不能清晰进行器件健康等级划分的问题,本文采用K-means 聚类算法对图9 中第1、2、3、4、5、9、13 组数据所对应的马氏距离进行重新划分,可以得到与二极管和MOS 管健康状态相关的4 个互不重叠的“簇”,如图10 所示。图10a 中,二极管老化过程数据聚类分析的分类结果与图9a 所示原始数据仿真设置的组别一致,而图10b 中,MOS管老化过程数据聚类分析的分类结果与图9b 所示原始数据仿真设置的组别有所差别。图10b 中圈出了聚类划分的结果和仿真组原始设置不一致的数据点。例如圈1 圈出的数据点,按原始数据仿真设置应为第2 组,但聚类划分结果为第1 组。可以看出,进行聚类划分前,按仿真组原始数据划分的4 个数据集之间的马氏距离存在重合点;在进行聚类分析之后,4 个数据集之间的马氏距离不存在重合点,被清晰地划分。根据马氏距离的聚类结果将图7 中解耦后的老化特征参数CPD和CPM相应地划分成4组,对应整流二极管和功率MOS 管的四种健康状态等级:优、良、中和差。
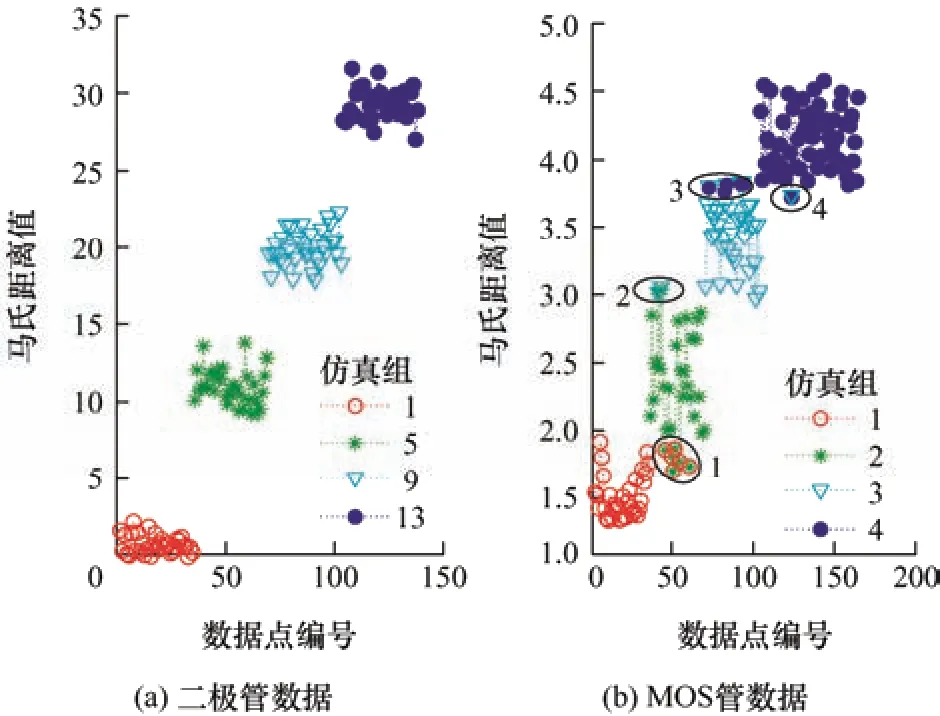
图10 马氏距离聚类分类结果
为了验证分类函数的有效性,本文按照表2的仿真设置重新生成16 组蒙特卡罗仿真数据,将全部老化数据代入上述生成的整流二极管和功率MOS 管的健康状态等级分类函数,进行器件健康状态的评估。评估的结果分别如表4 和表5所示。

表4 整流二极管健康等级的分类结果

表5 功率MOS 管健康等级的分类结果
将表4 和表5 中的分类结果与老化特性参数原始设置分组相比较,经过统计,关于二极管的4 种健康状态评估结果与老化特性参数原始设置的二极管四个老化阶段的匹配度为100%;关于MOS 管的4 种健康状态评估结果与老化特性参数原始设置的MOS 管四个老化阶段的匹配度为91%。
6 结论
采用数据驱动的方法实现了飞机主电源系统关键器件健康状态的评估。
(1) 确定了飞机主电源系统中故障率较高的关键器件为旋转整流器中的整流二极管和调压器中的功率MOS 管,并对关键器件的老化特性进行了分析。
(2) 通过飞机主电源系统老化模型的蒙特卡罗仿真,获取了大量系统处于各种工况条件的仿真数据,从中筛选出了可用于表征发电机健康状态的特征变量为系统励磁机的励磁电压和励磁电流平均值。
(3) 分析了工况的变化对系统特征变量的影响,确定系统状态评估时需要在相同的工况条件下采集数据,以排除工况改变对特征变量产生影响,从而避免导致评估结果的误判。
(4) 采用主成分分析方法对系统老化过程中采集的特征变量数据进行解耦,得到了两个关键器件的老化表征参数CPD和CPM,利用高斯混合模型建立了关键器件的健康基准模型,并计算了老化参数与健康基准模型的马氏距离,将马氏距离数据经过K-means 聚类后得到“标签化”的老化数据训练样本集,分别训练得到两个关键器件的神经网络分类函数。
(5) 利用蒙特卡罗仿真获得的大量数据对训练完成的神经网络分类函数进行了验证,数据的匹配度说明了该研究方法的有效性。

