低开关频率下五电平逆变器双波段特定谐波消除方法*

李国华 苑朝鸣

(辽宁工程技术大学电气与控制工程学院 葫芦岛 125105)

1 引言

近年来，多电平逆变器在中压高功率领域中被广泛应用[1]。典型多电平逆变器包括二极管钳位逆变器(Neutral point clamped，NPC)、电容钳位逆变器(Flying capacitor，FC)和级联H桥型逆变器(Cascaded H-bridge，CHB)等[2-3]，以上常用多电平逆变器结构开关器件较多，结构复杂。文献[4]提出一种改进式U 型单元封装MPUC 多电平逆变器拓扑。在输出相同电平的情况下，该逆变器结构简单，功率开关器件少，使得在低开关频率下逆变器消除特定谐波的开关次数减少，并且具有输出电压稳定的优点。目前，大功率开关器件逆变器已经在可再生能源发电、电力系统运行和机车牵引等领域广泛应用[5-6]。然而随着功率的变大，开关损耗也随之增加，为了提高开关器件的平均寿命和逆变器的输出功率[7]，在各种调制技术中SHEPWM 技术可以以较低的开关频率、较少的开关损耗，输出较好的电能质量[8]。该技术的原理是选择合适的开关角度来消除低阶谐波[9]。SHEPWM 技术的难点是求解非线性方程组，求解方法可分为线性求解和非线性求解。文献[10]应用Walsh 函数分析Walsh 域与傅里叶域之间的变换关系，将非线性方程组转化为线性方程组进行求解，为SHEPWM 在线实时求解提供可能，但该算法需要求解所有开关角表达式，计算量大，并且初值选取范围较大。文献[11]采用线性插值法和牛顿迭代法实现开关角在线计算，线性插值法会占用大量的DSP 存储空间，牛顿迭代法有时会出现迭代不收敛的情况。文献[12]应用Groebner 基和对称多项式理论将阶梯波SHEPWM 非线性方程组转换为一元高次多项式方程以及一组线性方程组求解，但求解过程复杂，计算量较大。对于非线性求解方法，实现实时求解较为困难，需要把离线计算的开关角度存储在DSP 中，并且求解结果容易出现局部最优解，造成特定次谐波消除不能达到理想状态。近年来通常利用智能算法对SHEPWM 非线性方程组进行求解。文献[13]采用粒子群优化算法，该方法流程简单，参数设定少，但搜索能力较差，容易陷入局部最优解。文献[14]采用蚁群优化算法，虽然具有强大的寻优能力，但算法所需时间较长。上述各类求解方法在求解多电平逆变器SHEPWM 消谐方程组时，在调制度较低情况下非线性方程组无解，限制了SHEPWM 方法的实际应用。文献[15-17]通过建立多个波段的谐波消除方程组，利用Walsh 函数、多种群遗传算法、三角余弦函数倍角关系求解出低调制度下的开关角度，但依旧存在求解过程中需要设定初值、求解过程计算量大、容易出现局部最优解、调制度较低时THD 较大的问题。

本文利用三角函数公式和设定约束条件将非线性方程组转化为线性方程组进行求解，为SHEPWM在线求解实时控制提供可能。针对五电平逆变器在低调制度下非线性方程组无解问题，将新方法应用到双波段调制策略中；建立双波段SHEPWM 消谐模型，消除五电平逆变器的5 次谐波；并将所提方法与智能算法比较，得到两种方法的全调制度范围内的开关角轨迹与THD 值；最后以仿真和试验证明新方法求解的可行性和正确性。

2 五电平MPUC 逆变器拓扑结构

五电平MPUC 逆变器拓扑结构如图1 所示，以图2 所示单相五电平MPUC 逆变器为例说明。该结构由两个直流电源E和3 对IGBT 功率开关器件组成。

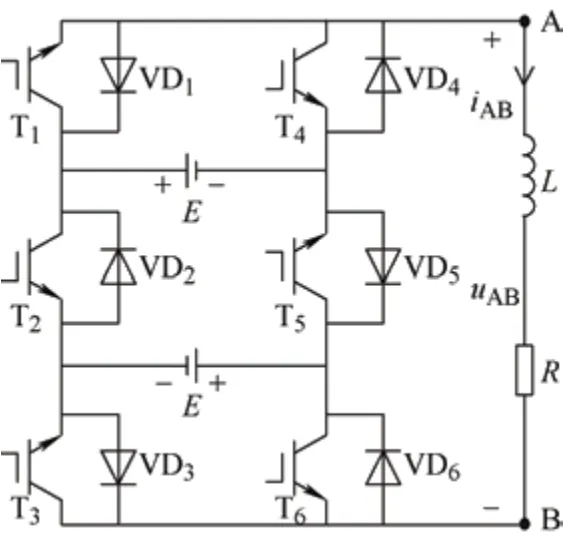
图2 单相五电平MPUC 逆变器拓扑

逆变器开关状态如表1 所示，当T1、T3、T5导通时，直流电压源串联，电流由A 到B，相电压uAB等于2E，同理当开关T2、T4、T6导通时，电流由B到A，相电压uAB等于-2E。以此类推，从表1 可以看出3 组开关器件一共有8 种开关状态，输出五种电平：-2E，-E，0，E，2E。不需要使用所有冗余的交换状态，只使用1、2、4、6、8 状态来触发MPUC 逆变器。

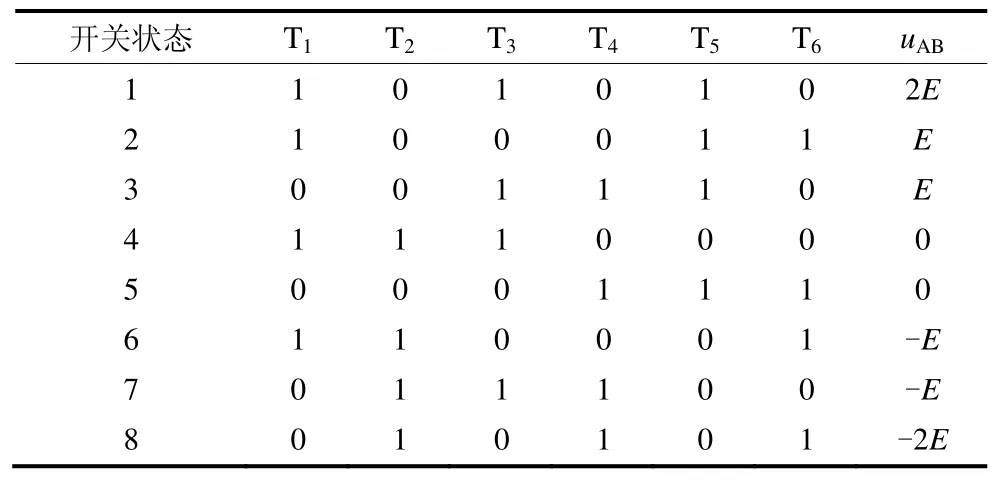
表1 单相MPUC 逆变器开关状态表

3 五电平逆变器双波段SHEPWM 消谐模型

由于五电平逆变器求解SHEPWM 非线性方程组时，调制度较低时方程组无解，为了得到低调制度下的开关角度，将图3 中A 波段2E电平向下折叠，得到图3 的B 波段调制模式。双波段调制模式的建立使调制度拓展到[0,1.15]。

图3 五电平逆变器双波段SHEPWM 波形

五电平逆变器SHEPWM 波形如图3 所示。该电压波形可由式(1)傅里叶级数表示。

由于输出电压波形为奇函数并且1/4周期对称，αn=α0=0。故式(1)可简化为

各次谐波幅值βn可由式(3)表示

式中，m为1/4 周期内开关角数；αm为第m个开关角度；pm在αm上升沿记+1，在αm下降沿记-1。αm范围为0<α1<α2<…<αm<90°。

调制度M为

根据式(3)可得，对于五电平逆变器，A 波段其消除五次谐波的消谐模型可以用方程组(4)来表示

B 波段其消除五次谐波的消谐模型可以用方程组(5)来表示

4 五电平逆变器双波段谐波消除新方法

为了确定开关角度，针对A 波段，将式(4)由三角函数公式化简为式(6)

由于式(6)第一个方程为零，根据三角函数性质，设定两组满足第一个方程成立的约束条件可由式(7)表示

由于0<αm<90°因此k=1。约束条件α1+α2=π/5代入式(6)求得开关角不满足αm的求解范围，因此将代入式(6)得到式(8)。

化简式(8)得

求解线性方程组式(9)得到调制度M的调制范围为0.375～1.15 的开关角。

针对B 波段与A 波段同理可得

通过求解线性方程组式(10)得到调制度M的调制范围为0～0.374 的开关角。

新方法通过求解两组线性方程式(9)、(10)得到了调制区间为[0,1.15]的开关角度。为了更好地反映新方法在求解五电平逆变器双波段SHEPWM 消谐方程组的优越性，在消除相同谐波次数，并同样应用双波段调制策略情况下，选择粒子群优化算法(Particle swarm optimization，PSO)，在开关角度和THD 两个方面比较。PSO 算法求解精度较高，求解适应度函数结果更趋近于零，因此更接近同等条件下进行比较。PSO 在求解过程中容易出现局部最优解问题，可以通过多次求解避免该问题。两种求解方法的开关角度如图4 所示。相、线电压全调制度THD 对比图，如图5、图6 所示。

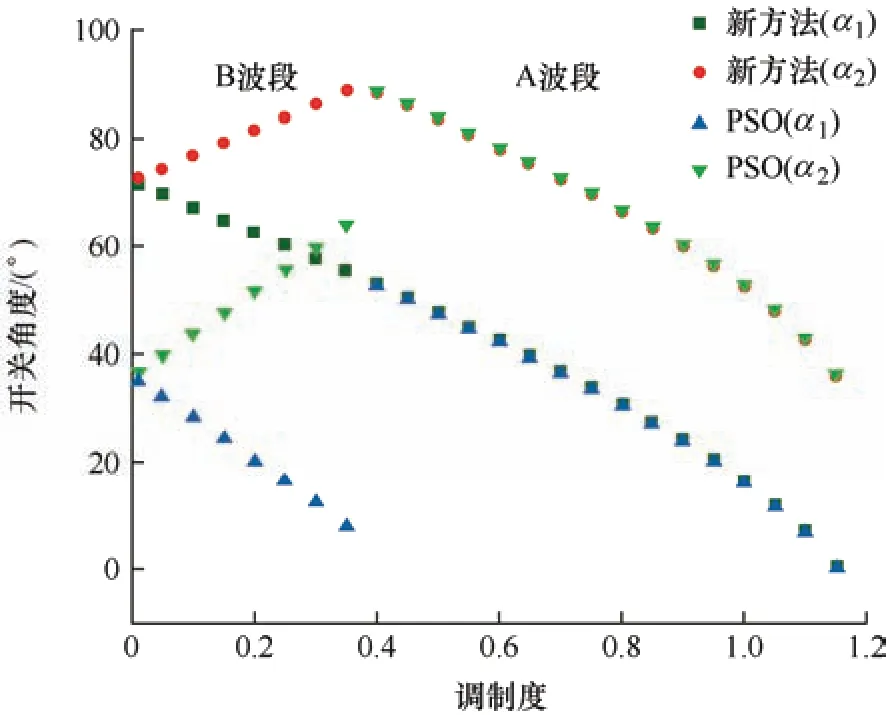
图4 全调制度开关角度轨迹图

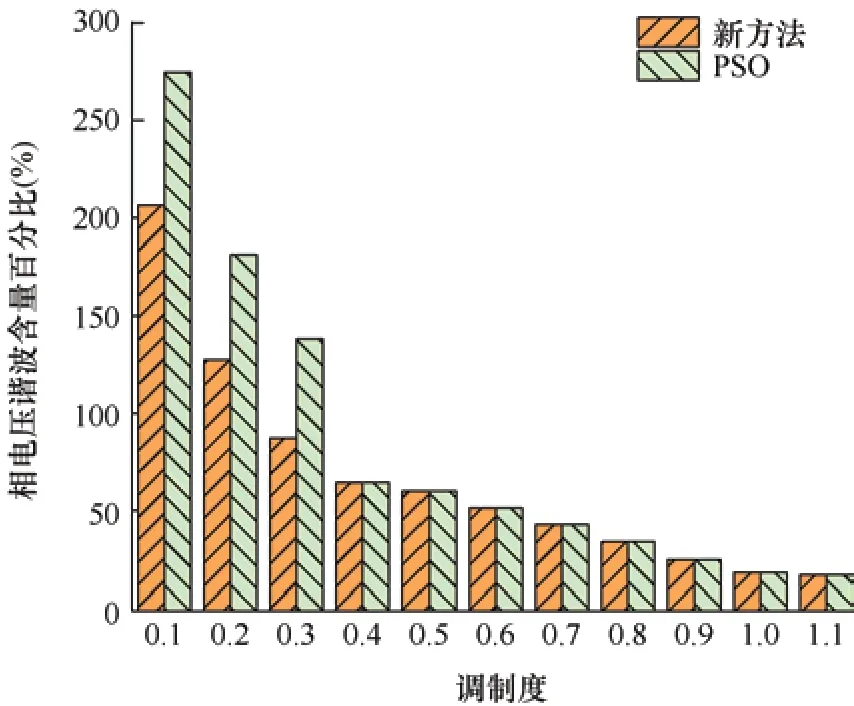
图5 相电压全调制度谐波含量对比图

图6 线电压全调制度谐波含量对比图

由图4 可知，通过两种方法求解五电平逆变器双波段SHEPWM 消谐模型的开关角，在A 波段角度近似一致，但是在B 波段角度不同。通过比较各个调制度下相、线电压的THD 值，如图5、图6 所示。从图5、图6 中看出，在B 波段低调制度下，新方法具有较好的THD 值，改善了因增加B 波段扩大调制度所引起THD 值较高的问题。

5 五电平MPUC 逆变器SHEPWM 仿真分析

为了验证新方法求解SHEPWM 方程组的正确性，以A 波段调制度M等于0.9 和B 波段调制度M等于0.3 为例，利用Matlab/Simulink 进行仿真研究。系统仿真参数如下：仿真时间为0.06 s，逆变器输出端电抗器为10 mH，电阻为5 Ω；直流侧参考电压为12 V。图7 为采用A 波段调制逆变器输出相电压和线电压波形图，图8 为采用B 波段调制逆变器输出相电压和线电压波形图，图9、图10 分别给出了两个波段下相电压和线电压的基波电压幅值和THD 值。

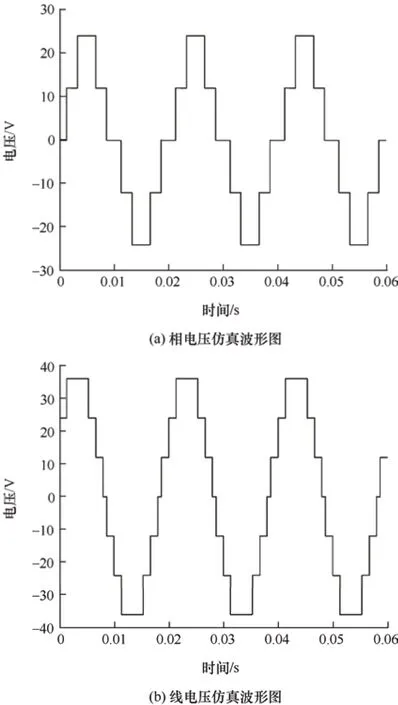
图7 A 波段下相电压与线电压仿真波形图

图8 B 波段下相电压与线电压仿真波形图

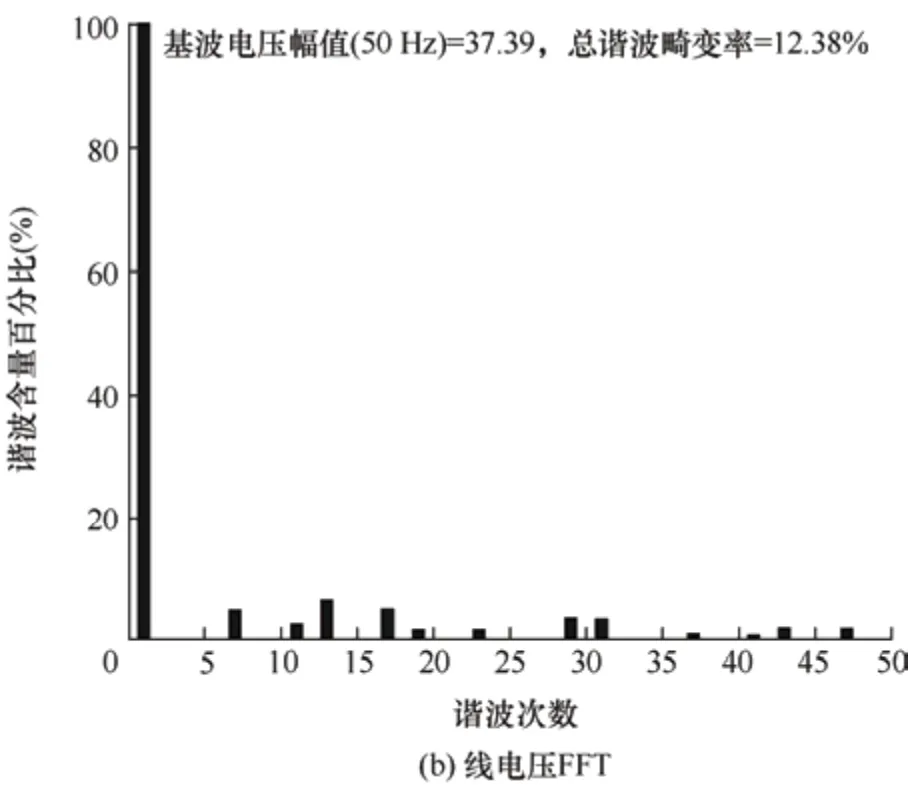
图9 A 波段下相电压与线电压FFT 分析

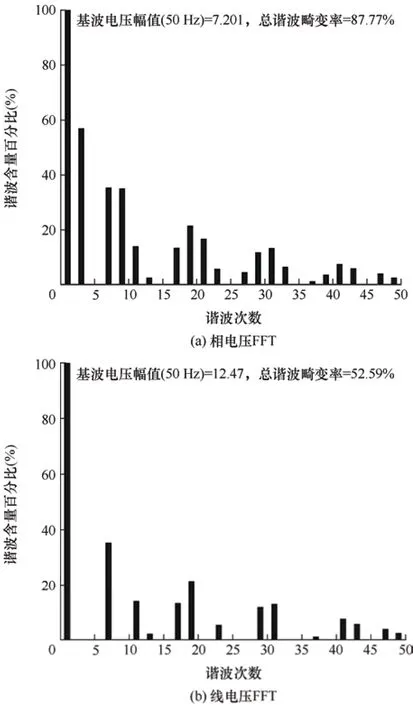
图10 B 波段下相电压与线电压FFT 分析

由图7 可见，五电平MPUC 逆变器采用A 波段调制时输出相电压与线电压为梯形波。由图8 可知，五电平MPUC 逆变器采用B 波段调制时输出相电压与线电压波形最高电平通过向下折叠拓展调制度。由图9、图10 的FFT 分析可知，在双波段调制模式下5次谐波完全消除。仿真结果证明，采用新方法与拓展调制度的双波段SHEPWM 控制方法结合是可行的。

6 五电平MPUC逆变器SHEPWM试验

同仿真参数一致，搭建系统试验样机如图11所示。 系统主控芯片采用 32 位 DSP(TMS320F28335)；逆变器主电路选用 IGBT(BSM50GB120DN2)作为功率开关器件；试验中示波器型号为DS1052E。图12 为在仿真基础上逆变器A 波段输出相电压和线电压波形，图13 为逆变器B 波段输出相电压和线电压波形。图14、15 为对应的FFT 试验波形。

图11 试验样机

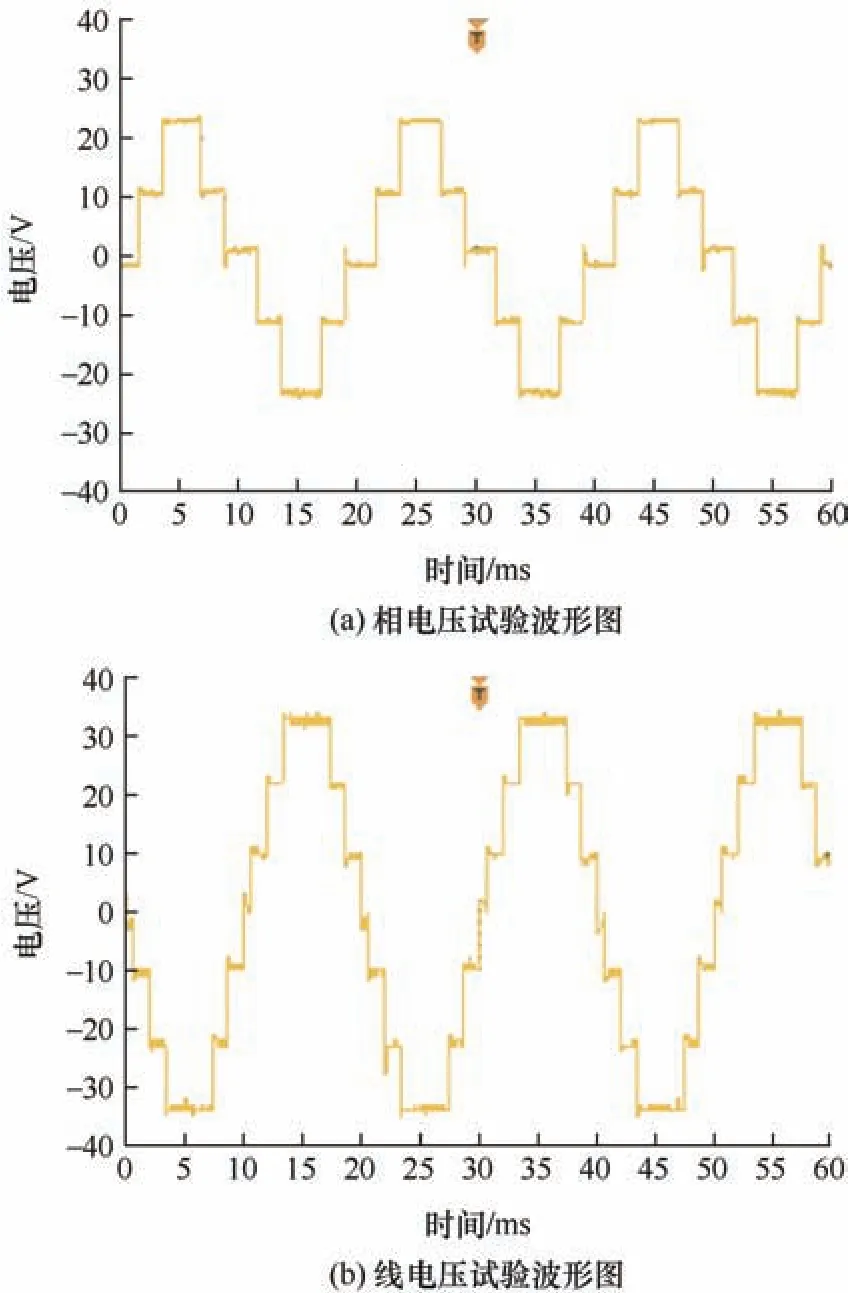
图12 A 波段下相电压与线电压试验波形图

图13 B 波段下相电压与线电压试验波形图

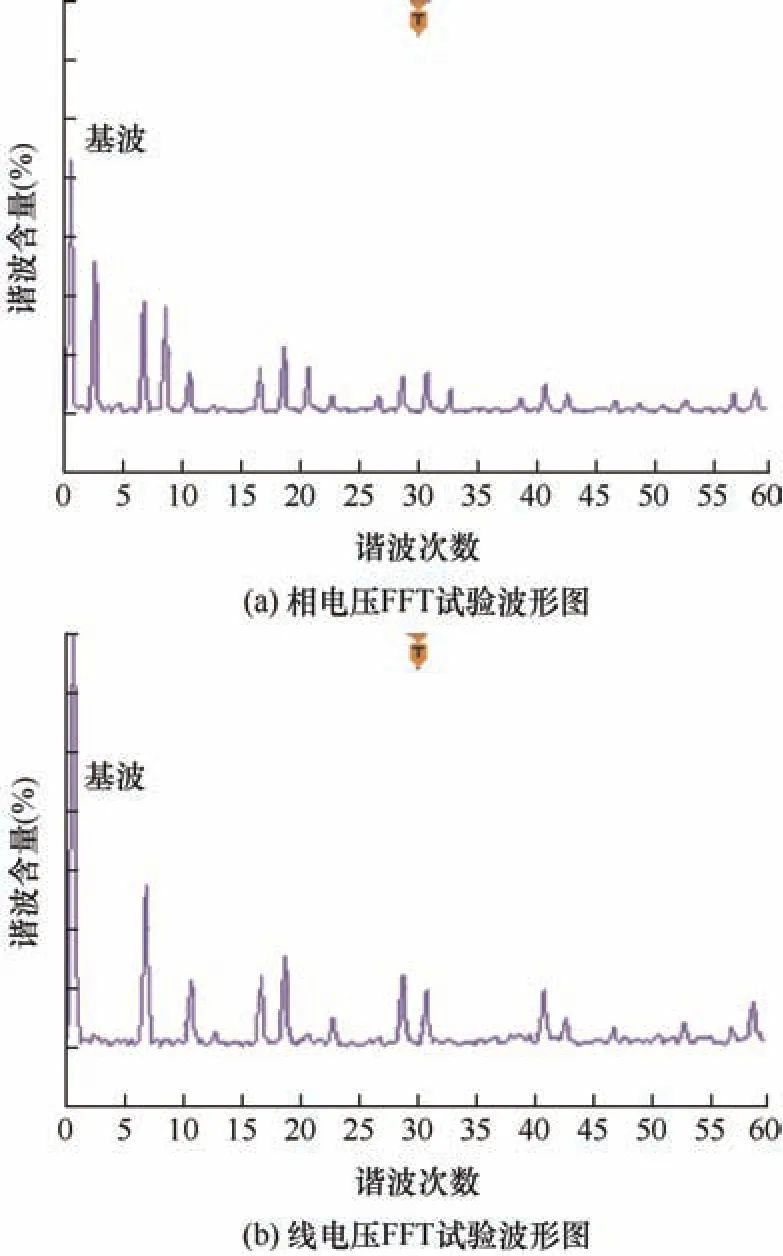
图15 B 波段下相电压与线电压FFT 试验波形图

如图12、13 所示，五电平MPUC 逆变器双波段输出相电压与线电压与仿真波形一致，图14、15所示的FFT 试验波形中5 次谐波得到有效消除。试验证明了新方法和双波段结合求解开关角度的正确性。

7 结论

本文以五电平MPUC 逆变器为研究对象，通过仿真与试验结果证明了新方法与拓宽调制度的双波段SHEPWM 控制策略结合的正确性和可行性，为求解低开关频率下多电平逆变器SHEPWM 的非线性方程组提供了一种新的方法。与传统方法相比，新方法有如下优点。

(1) 解决了五电平逆变器在低调制度下非线性方程组无解问题，较好地满足了电机类装置的调速要求。

(2) 该方法无需给定初始值，求解过程简单，并且避免了局部最优解问题。

(3) 改善了在B 波段低调制度时THD 值较高的问题。