基于降阶解耦的五相容错伺服电机驱动系统容错控制策略*
薛荣泽 蒋雪峰 孙延超 汤欣喜 高宇飞 魏之建 马 凯
(1.南京理工大学自动化学院 南京 210094;2.中国航天科工南京晨光集团有限责任公司 南京 210006)
1 引言
导弹舵机是导弹飞行控制系统的重要组成部分,是导弹方向控制的执行机构。导弹舵机系统是一个高精度的位置伺服系统,导弹能按照一定轨迹在空间中飞行,需要舵机带动并随时校正方向,因此导弹舵机的性能将直接影响导弹的动态品质和命中目标的准确率[1]。由于电动舵机伺服系统简单可靠、易于控制且成本较低,对电动舵机伺服系统的研究在军事科技领域引起了许多学者的关注和深入研究[2-3]。随着电力电子技术和交流伺服技术的不断发展,目前电动舵机已经得到了广泛的应用,提高了高性能电动舵机伺服系统研究开发的可能性[4]。而电动舵机系统采用电机驱动,不可避免会出现电气故障[5],电驱动系统中开路故障是最常见的故障类型之一,若发生故障后未采取容错控制策略,将会导致绕组过热、绝缘损坏、转矩降低的一系列问题,甚至会损坏整个系统[6-9]。因此,目前国内外研究的主要方向之一就是开路故障下多相电机的容错控制策略。
传统电动舵机多采用三相永磁同步电机的三环位置伺服系统[10]。而传统三相永磁电机的三相半桥驱动系统在发生缺相故障后无法进行容错运行,在需要可靠性应用的场合,通常采用具备容错能力的三相永磁电机拓扑系统来实现电机的容错运行[11-12],但是也会带来体积重量大、系统利用率低以及无法抑制短路电流等问题。而相较于传统的三相永磁电机驱动系统,多相永磁电机驱动系统具有更高的功率密度,高控制自由度和强容错能力等特点[13-14],高控制自由度使得电机能够在不增加任何额外硬件措施的情况下实施容错控制,将其应用于导弹舵机系统中可以解决传统三相永磁电机驱动系统在采用容错拓扑时系统结构复杂的问题。
针对多相电机控制策略和容错运行策略的研究,文献[15]建立了五相永磁电机开路故障后基波电流平面与三次谐波电流平面的关系,通过离线计算求得了三次谐波平面的扰动系数,通过注入三次谐波的方法减少了故障带来的转矩脉动,并且缩短了运行模式的切换时间,该方法有效地减少了故障带来的转矩脉动。文献[16]基于故障前后旋转磁动势不变的原理,重构了剩余自由相电流的幅值和相位,实现电机的容错运行,但由于采用电流滞环控制,存在开关频率不固定和电流波动大的问题。文献[17]通过分析不同情况下缺相容错电流的表达式,提出二次旋转变换对电机磁场定向解耦,该算法可以提高电机的容错运行能力,但其计算复杂度高。文献[18-19]基于五相永磁电机提出模型预测电流控制的方法抑制共模电压,并在代价函数中引入了三次谐波电流有效减小了谐波电流占比。文献[20]基于五相电机采用模型预测转矩控制实现容错控制,通过查表的方法筛选可以利用的矢量集合,从而减小了遍历次数,简化了运算过程。但现有研究鲜有对多相永磁电机伺服系统的容错性能进行研究,有待于进一步研究多相电机伺服系统的容错控制策略。
本文针对现有导弹电动舵机系统功率密度低和容错拓扑电路系统冗余利用率低的问题,提出一种基于降阶解耦的五相容错伺服电机(Permanent magnet fault-tolerant servo motor,PMFSM)驱动控制系统的单相故障容错控制策略。首先,提出了适用于单相开路故障的Clark 和Park 变换矩阵,得到了单相开路故障下的电机解耦控制模型;然后,对故障后不对称运行而引起的中性点偏移问题进行电压补偿,在此基础上推导出单相缺相后的基本空间电压矢量,在基波平面采用虚拟矢量法,用8 个利用率较高的基本矢量合成4 个虚拟矢量,再利用2 个基本电压空间矢量,将基波平面分成了6 个扇区,通过对6 个扇区的划分和6 个非零空间电压矢量的合成得到基波平面的参考矢量,在3β脉振轴上只需要用到2 个方向的4个非零矢量就可以实现对脉振轴空间电压矢量的合成,为抑制两个子域的耦合,矢量的作用时间有一定的约束关系,可以实现两个子平面的共同调制;最后,针对上述控制策略,进行了仿真和试验的分析,结果均验证了上述容错控制策略的正确性。
2 五相PMFSM 驱动系统
一种基于五相PMFSM 的驱动系统结构如图1所示,其包括一台五相PMFSM,一套五相半桥逆变器和一个独立的400 V 直流电源。由于五相容错伺服电机的高控制自由度,可以在发生单相绕组开路故障时仍具有3 个自由度,因此在不增加任何硬件措施下就可以实现电机的容错运行,具有强容错性和高电气隔离能力。
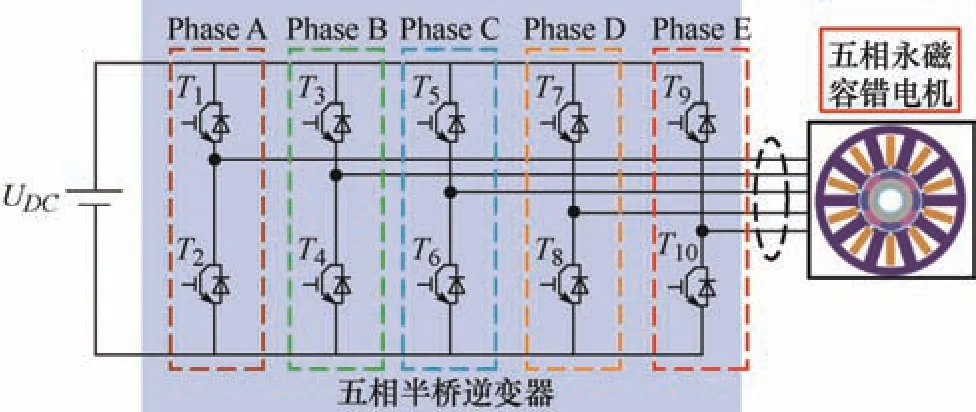
图1 五相PMFSM 的驱动拓扑
五相PMFSM 的本体如图2a 所示,绕组分布如图2b 所示,电机采用10 槽8 极分数槽双层集中绕组结构,两相槽间隔电角度为144°,绕组无重叠,具备端部绕线少、用铜量少、能较好地抑制谐波、电机输出转矩脉动小等优点。

图2 五相容错伺服电机结构图
五相PMFSM 应用于高可靠性的场合,需要具备容错能力,在定子绕组单相开路故障下,本文以A 相为例,在A 相开路故障磁力线图如图3a 所示,可以发现故障后各相绕组磁力线无耦合,电机有良好的磁隔离能力;五相PMFSM 在A 相开路故障后磁密云图如图3b 所示,可以看出定子齿和定子磁轭在故障后的最大磁通密度不超过1.8 T,而所采用电机的硅钢片饱和磁通密度为2.2 T,满足设计需求。
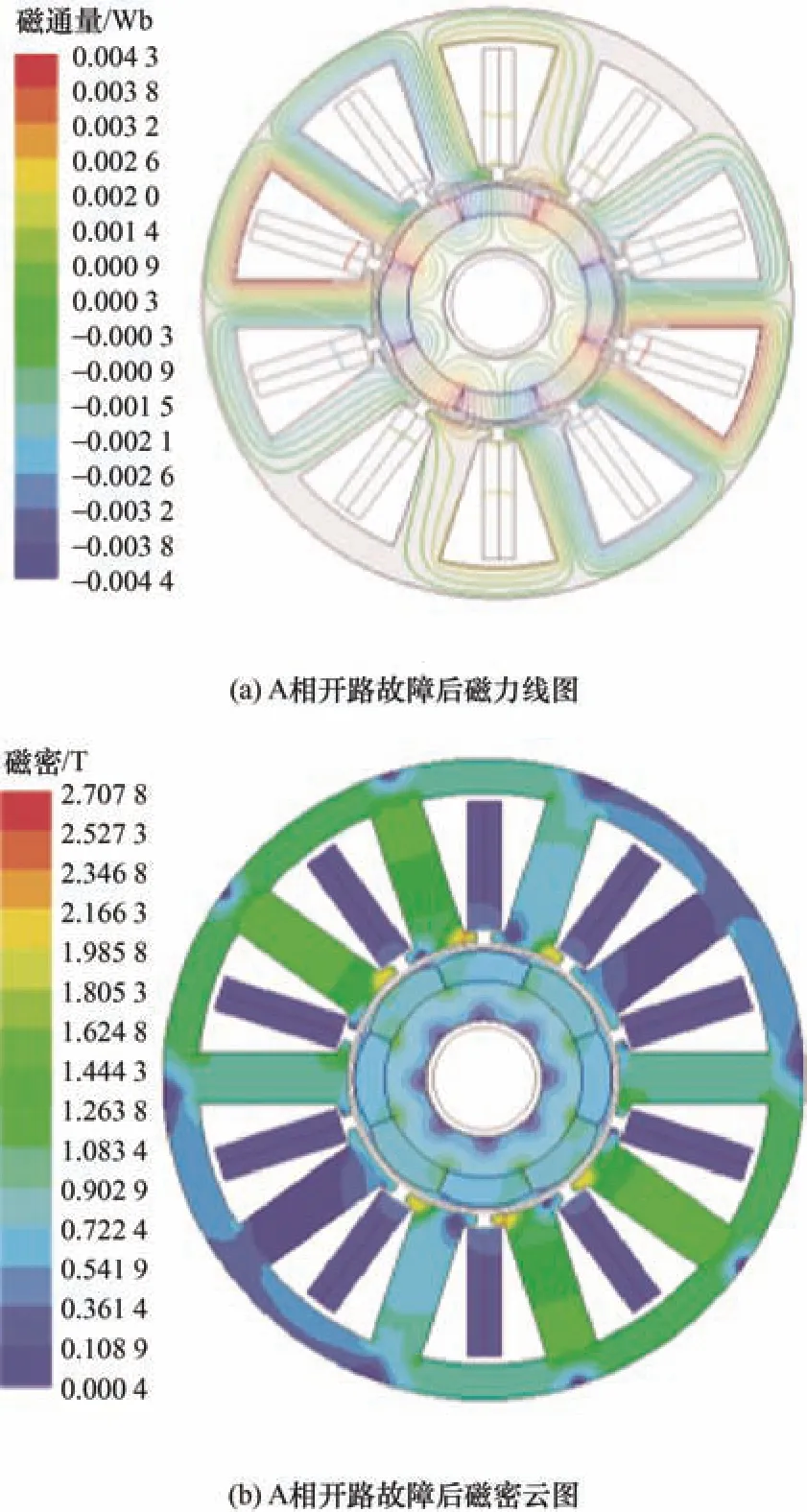
图3 开路故障后五相PMFSM 磁力线和磁密云图
3 五相PMFSM单相开路容错控制策略
五相PMFSM 伺服系统单相开路故障下容错控制策略框图如图4 所示,主要由五相PMFSM、位置控制器、转速PI 控制器、电流PI 控制器、坐标变换算法模块、正常空间矢量脉宽调制(Space vector pulse width modulation,SVPWM)算法模块、容错SVPWM算法、逆变器等构成。当发生故障后,通过分别将正常状态的坐标变化模块和SVPWM 算法模块切换至对应故障状态下的降阶坐标变换模块和容错SVPWM 算法模块来实现五相PMFSM 的容错运行。

图4 五相PMFSM 伺服系统容错控制框图
3.1 单相故障下五相PMFSM 降阶解耦变换
在发生单相开路故障后,电机控制的自由度减小,对应的变换矩阵要进行降阶处理,本文以A 相为例,此时剩余有效相B、C、D、E 四相,加以零序电流的约束,此时的五相永磁电机有3 个自由度,可以得到该故障下的降阶Clark 矩阵为
当故障发生后,保证定子空间任一位置角上的定子磁动势与正常模式保持一致,理论上便可以实现五相电机在开路故障模式下的容错运行。根据定子磁动势的约束条件,可以推导出定子电流的表达式,采用零序电流去修正系数矩阵的第一行向量,即对式(1)进行矩阵初等变换,修正后的容错控制电流配置为
式中,修正系数i=1 。此时电机有3 个自由度,分别是1α轴、1β轴构成的基波平面和三次谐波平面的β3轴。由于三次谐波平面只有一个控制自由度,因此空间电压矢量只能在β3正负轴上下脉动。由于电机故障后自由度降低,因此只可以保证基波磁动势在故障前后不变而无法维持三次谐波磁动势不变。
旋转变换用以将故障后静止坐标系下的电流投影到旋转坐标系下,从而将交变量转化为直流量。而单相故障后的3 个自由度只可以使得1α与1β平面的交变量转换为直流量,因此故障后的旋转变换对基波平面进行Park 变换,而只对三次谐波平面作简单的恒等变换。此时的降阶Park 变换矩阵为
式中,θ为电机的电角度。
经过上述两种坐标变换,可以实现A 相故障下五相PMFSM 的降阶解耦,通过分别控制3 个维度的电流实现电机在单相开路状态下的容错运行。
对单相开路故障后的五相PMFSM 降阶解耦后,采取id= 0控制,在不明显增加额外电磁转矩波动的情况下,谐波电流的给定主要有两种约束:最小铜损约束和相电流等幅值约束。
最小铜损约束要求基波电流和谐波电流平方和最小,对于五相PMFSM 驱动系统,令=0即为最小铜损给定。
通过变换逆矩阵求得最小铜损约束下各相的电流配置为
相电流等幅值约束能实现故障后剩余有效相电流幅值相等,此时剩余有效相电流关于故障轴线对称,以A 相开路故障为例,即引入了新的约束ib=-id和ic=-ie,通过分别将自然坐标系和旋转坐标系的电流投影在β1轴和β3轴后建立等式,求解得=0.236cosθ。
相电流等幅值约束中需要引入基波平面的q轴电流给定和转子位置角θ,为简化控制系统,本文采用最小铜损约束给定,即故障后控制系统的3 个维度的电流给定配置为通过前向的PI 控制器输出给定,如图4 所示。
3.2 单相故障下五相PMFSM 的SVPWM 算法
以A 为例,A 相开路故障下,逆变器有效相电压可用开关状态矢量表示为
逆变器驱动下的五相电机的端电压存在如下约束关系
由式(5)和式(6)可以得到
在单相故障的影响下,电机的中性点电位会发生偏移,这样的电压偏移会对SVPWM 算法产生影响。为消除此影响,本文在控制算法的前向通道中进行电压补偿,用补偿后的电压作SVPWM 算法的输入电压进行调制,以A 相开路故障为例的电压补偿过程如下
式中,v1α、v1β、v3β分别是电压补偿后电机端电压在1α轴、1β轴和β3轴的分量。
则有
式中,TA_com为进行电压补偿后的修正降阶变换矩阵,表示为
驱动系统发生A 相开路故障时,该相所对应的电流为0,因此A 相端电压和A 相反电动势相等,vα1、vβ1、vβ3和原电压uα1、uβ1、uβ3存在如下关系
则补偿后端电压用开关函数表示为
此时的电压经电压补偿,不再受电机运行状态影响,可以对单相开路故障下五相PMFSM 的端电压进行矢量脉宽调制,基本空间电压矢量分布图如图5 所示。

图5 单相开路故障下空间电压矢量分布
为实现对基波平面的空间电压矢量的合成,考虑到基波空间电压矢量的利用率,选取V8和V13、V4和V14、V2和V7、V1和V11构成的四组虚拟空间电压矢量以及V6和V9两个基本空间电压矢量进行合成,所采用的虚拟电压矢量的作用时间需要满足式(13),以抑制β3轴上的伴生电压产生。这些矢量将基波平面划分为6 个扇区,如图6 所示。

图6 单相开路故障扇区分布
在确定参考矢量后需要计算矢量作用时间,求解过程可以是将参考矢量和相邻两矢量分别投影在α1、β1轴上,再加上式(13)的约束,可以构成满秩的非齐次线性方程组,求解得出所用到基本空间电压矢量的作用时间。由于用到虚拟矢量需要两个基本空间电压矢量,所以在第二扇区和第五扇区共需要4 个非零基本空间电压矢量,其余扇区只需要3个非零基本空间电压矢量即可。
此外,推导在β3脉振轴上的作用时间与上述过程类似,当参考矢量在正半轴时,用V5和V12两个矢量;在负半轴用V3和V10两个矢量。同时为防止在基波平面内产生伴生电压,需要满足如下约束
在分别求得各扇区作用时间后,可以实现对两个子平面共同调制,考虑到减小开关损耗,采用中心对称原则选择功率管开关顺序,零矢量作用时间不变,高电平采取中心对称处理。
4 仿真结果及分析
为对上述策略的正确性进行初步验证,本文基于Matlab 搭建了五相PMFSM 的驱动系统的容错控制策略仿真,系统结构主要有以下部分:五相PMFSM、五相电压型逆变器、电流PI 控制器、转速PI 控制器、位置控制器、正常SVPWM 算法模块和容错SVPWM 算法模块。基于Matlab 的模型可以实现五相容错伺服电机单相开路故障容错策略的仿真验证。
4.1 转速电流双闭环控制仿真
4.1.1 未采取容错策略
设置0.15 s 发生A 相绕组开路故障。电机绕组开路故障前后的五相容错伺服电机的电流、转速、转矩的仿真波形如图7 所示。

图7 未采取容错策略时A 相开路故障前后波形图
由图7a 可以看出,当A 相开路故障后,A 相电流变为0,而B、C、D、E 相电流发生严重畸变;由图7b 和图7c 可以发现,在A 相绕组开路故障后未采取容错策略时,转矩脉动很大,转速逐渐下降并有较大脉动,已经无法维持在给定值,若电机继续在故障下运行状态将会严重受损。
4.1.2 采取容错策略
设置0.15 s 发生A 相绕组开路故障并且同时采取容错控制策略。电机绕组开路故障前后的五相容错伺服电机的电流、转速、转矩的仿真波形如图8所示。
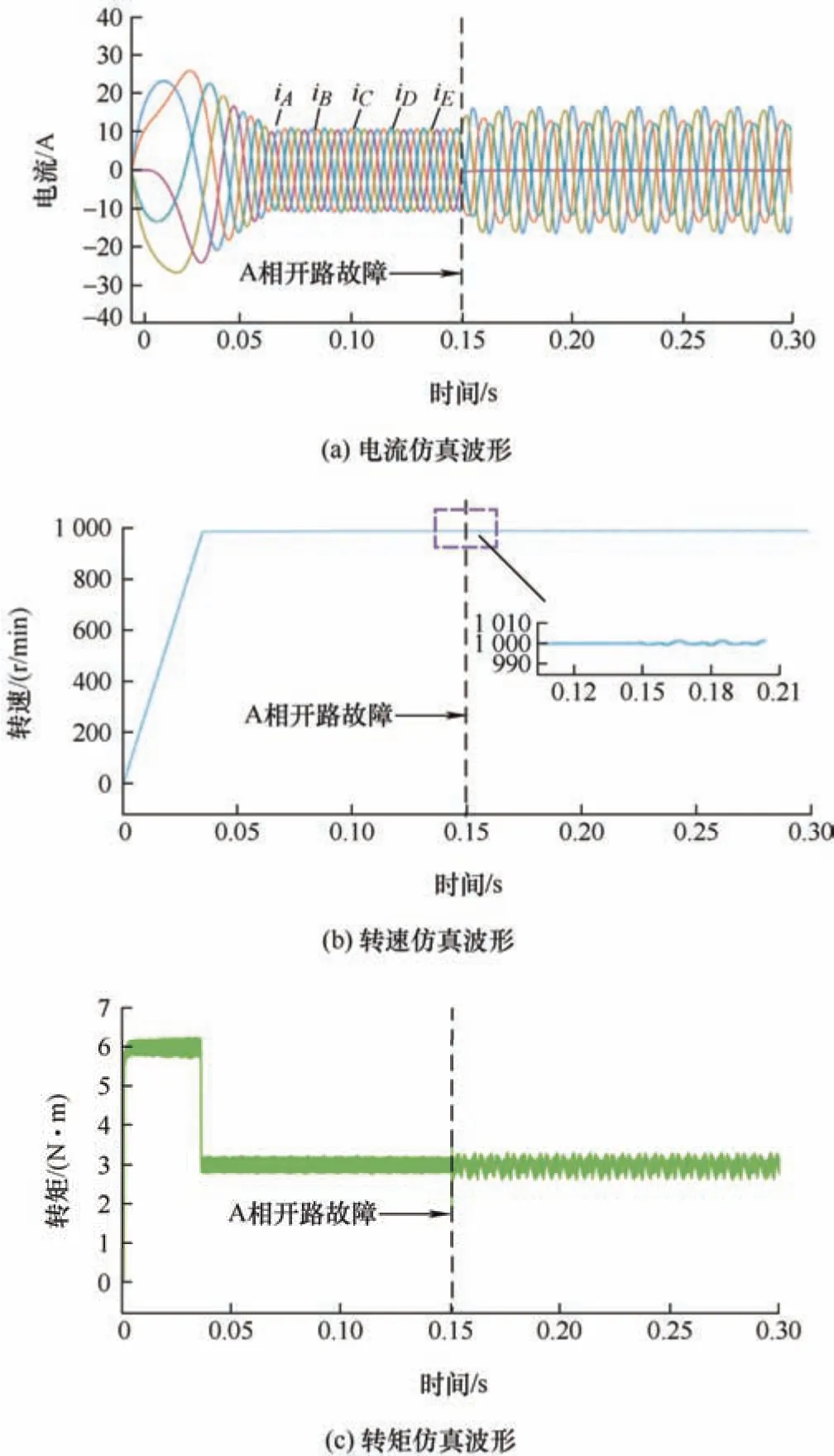
图8 采取容错控制时A 相开路故障前后波形图
在采取容错控制策略后,由图8 可以看出,A 相开路故障后A 相电流减为0,剩余健康相绕组电流能保持较好的正弦波形,各相电流幅值与理论分析一致;采取容错策略后,电机的转速在故障后仍然能跟随给定转速信号并保持稳定;采取容错控制策略后,电机的转矩脉动较小,与故障前基本保持一致,验证了容错控制策略的正确性。
4.2 三环控制仿真
4.2.1 未采取容错控制策略
在上述两闭环系统外再增加位置外环,给定转子信号为25 rad,设置0.15 s 发生A 相绕组开路故障。电机绕组开路故障容错前后五相容错伺服电机的电流、转速和转子位置的仿真波形如图9 所示。
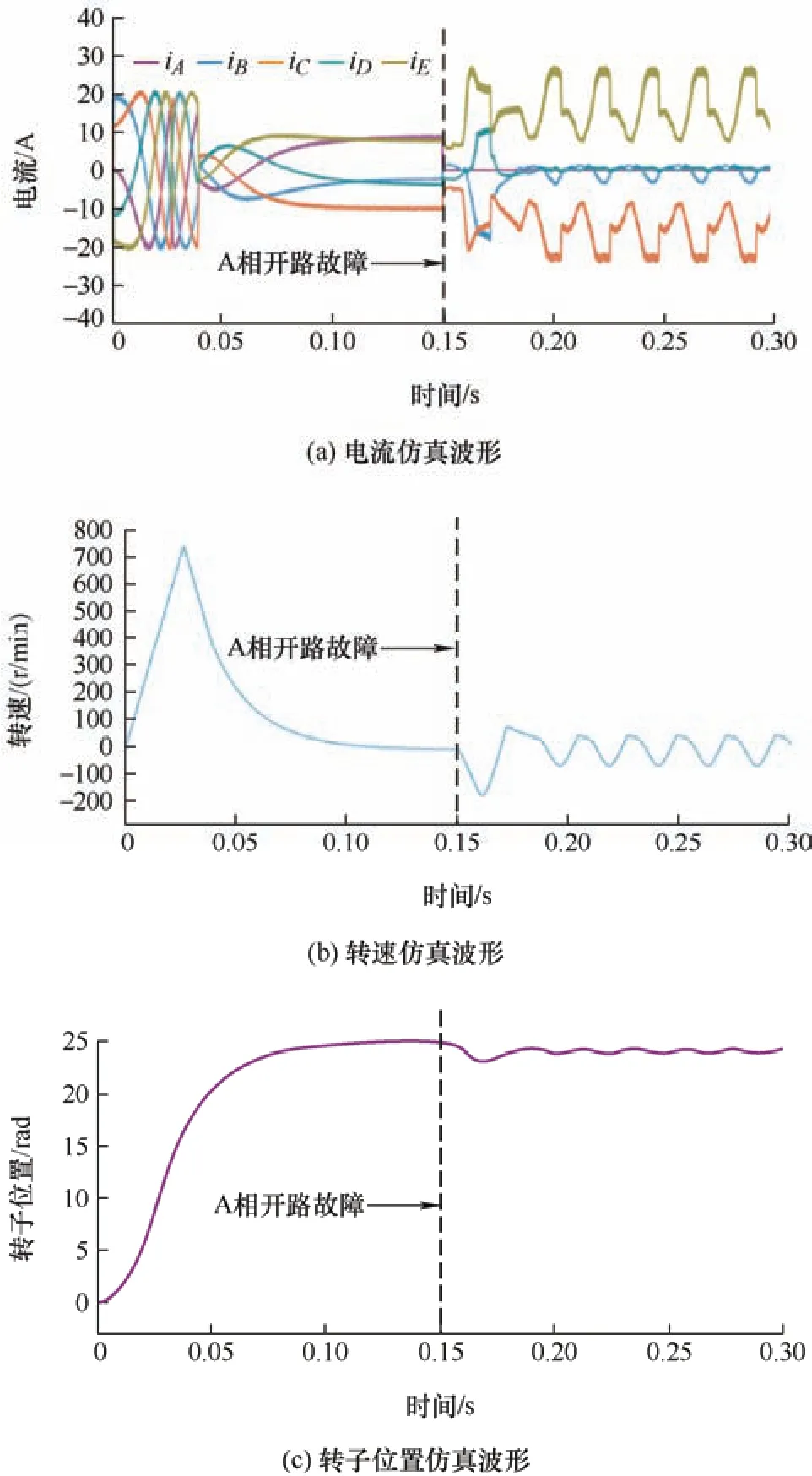
图9 未采取容错策略时A 相开路故障前后波形图
由图9 可以看出,当A 相开路故障之前,电机能够跟随在给定转子位置信号,并在达到指定位置后转速降为0;在A 相绕组开路故障后未采取容错策略时,A 相电流降为0,剩余有效相电流严重畸变,转速开始波动不能维持在0,转子位置不能保持在设定的信号位置。
4.2.2 采取容错控制策略
给定转子信号为25 rad,设置0.15 s 发生A 相绕组开路故障并同时采取容错算法。电机绕组开路故障容错前后五相容错伺服电机的电流、转速和转子位置的仿真波形如图10 所示。

图10 采取容错策略时A 相开路故障前后波形图
由图10 可以看出,当A 相开路故障之前,电机能够跟随在给定转子位置信号,并在达到指定位置后转速降为0;在A 相绕组开路故障后并采取容错策略时,转速仍然可以维持在0,转子位置保持在设定的信号位置不变,进一步验证容错策略的正确性。
5 试验验证
5.1 试验平台
五相PMFSM 系统驱动系统的试验平台如图11所示,试验平台组成如下:一台五相PMFSM、一台基于 DSP+FPGA 架构的实时数字控制器RTU-BOX204、模块化逆变器、示波器等。模块化的驱动器共有六相,可组成所需要的一套五相逆变器。主处理器采用了TI 公司的TMS320C28346,主频为300 MHz。五相PMFSM 由旋转变压器得到电机的转速与位置信号。

图11 基于五相PMFSM 驱动系统试验平台
5.2 转速电流双闭环控制系统
在五相PMFSM 空载运行过程中,将A 相断开并启用容错控制策略,试验波形如图12 所示。

图12 A 相绕组开路容错运行下试验波形
当A 相发生电机绕组开路故障时,A 相电流变为0,同时采取容错控制策略,使电机进入容错运行模式。发现在A 相绕组开路故障后五相PMFSM转速与正常运行一样,保持在给定转速,交轴电流iq也无明显的脉动,与正常状态的情况一致,表明五相PMFSM 在容错运行模式下转矩与正常运行模式的转矩相同。由此可见容错运行模式下转速试验与理论分析和仿真结果一致,验证了容错控制策略在五相PMFSM 转速电流两闭环控制系统中单相开路故障时的有效性。
由于处在稳态时转速环输出的给定= 0,会造成图中A 相电流波形有一定谐波。图13 是电机调速时的波形,给定转速增加的信号,但受到母线电压的限制,电机转速不能一直增加,此时的转速环输出,即q轴电流给定≠ 0,这时五相PMFSM的电流谐波较少。
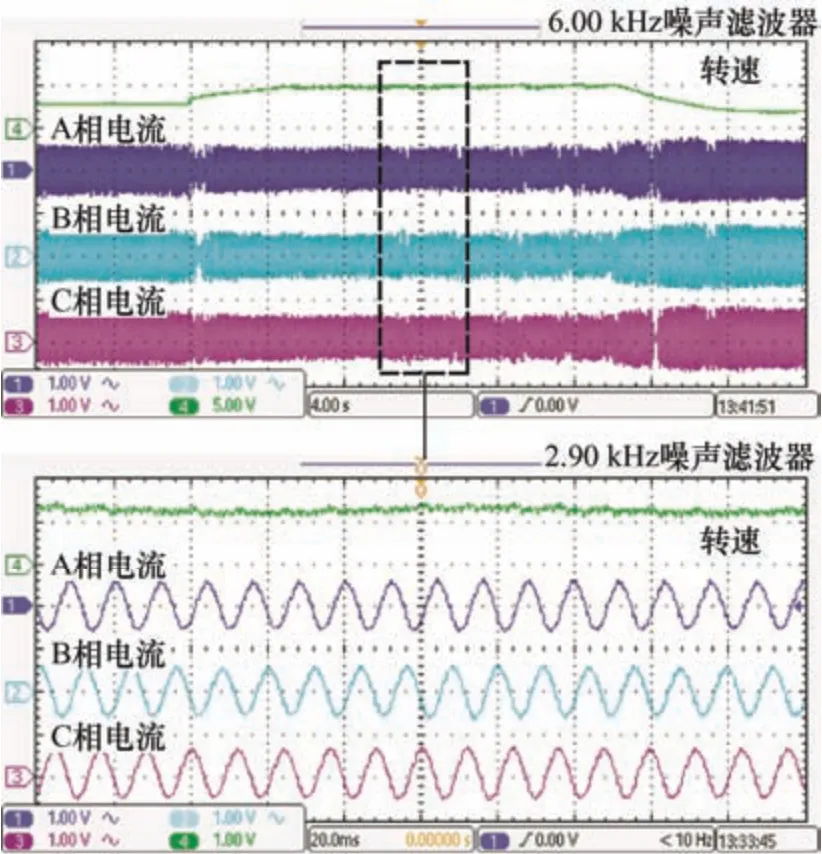
图13 调速波形及稳态放大图
试验的目的是验证容错策略的正确性,通过对比试验前后五相PMFSM 的运行性能验证容错策略的可行性,因此采用了基本的空载稳态的状态进行研究,电流波形有一定谐波对试验结论影响较小。
5.3 三环控制试验
验证双闭环控制系统稳定后,在双闭环控制系统基础上增加位置环,为验证基于五相PMFSM 三闭环控制系统的容错能力,在电机到达给定位置信号之前,断开A 相电机绕组同时采取容错控制策略,观察此时的电机位置信号和转速波形。
从试验波形可以发现,A 相绕组发生开路故障并容错运行后,五相PMFSM 的实际位置信号能够精准跟随给定位置信号,并在达到给定信号后转速降为0,由于试验采取M 法测量转速,M 法在低速情况下有一定误差,导致转速在降为0 时波形有毛刺(图14),从实际位置信号可以看出,电机转子位置较为平滑地跟随给定信号后保持在给定信号,进一步说明电机的实际转速较为平滑地降为0 后停转,因此控制策略能够实现五相PMFSM在单相开路故障下准确跟随给定信号,验证了电机控制的容错能力。
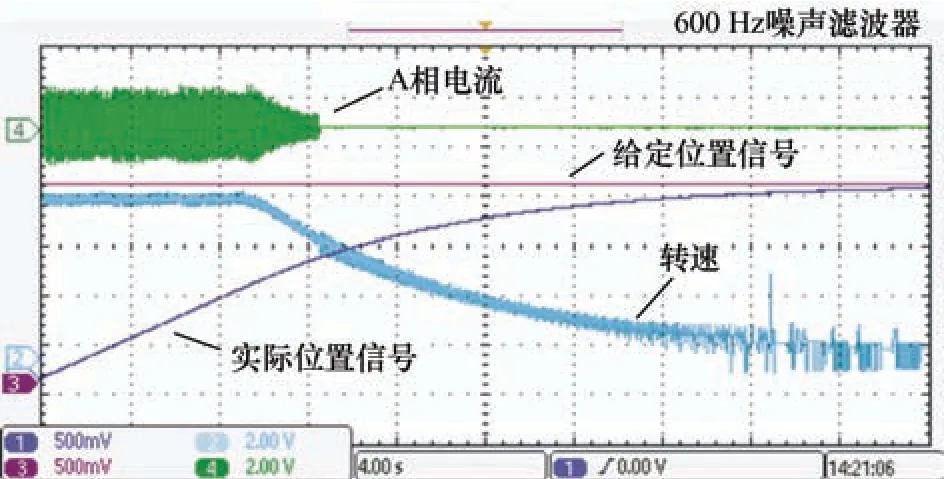
图14 A 相绕组开路容错运行下三环控制试验波形
6 结论
本文针对导弹电动舵机功率密度低以及常常存在电气故障的问题,提出了一种基于降阶解耦的五相容错伺服电机单相开路故障的容错控制策略,通过仿真和试验发现,驱动系统和控制策略有以下特点。
(1) 所提五相PMFSM 在单相故障后有较好的磁隔离能力,且最大磁通密度也不会超过硅钢片的饱和值。
(2) 该策略通过推导故障后的降阶变换矩阵,实现了对故障后电机模型的解耦控制,并推导了故障后电压空间矢量,分别对基波子平面和脉振轴的参考矢量的共同调制过程进行分析,推得了单相开路故障时五相容错伺服电机的容错SVPWM 算法,能实现五相PMFSM 在单相开路故障时的高可靠容错运行。
(3) 在五相PMFSM 发生单相开路故障后,采用该容错控制策略可以精准跟随给定信号,具有故障后容错运行的能力,能较好地适应导弹舵机恶劣且易受扰动的运行环境。
五相容错伺服电机驱动系统有优于三相永磁电机驱动系统更高的控制自由度和更强的容错能力,高控制自由度可以实现电机在不增加任何额外硬件措施下实施容错控制,可以避免三相永磁电机驱动系统在采取容错拓扑后系统变得复杂的问题。本文提出的五相容错伺服电机的容错控制策略能够确保系统在单相故障的情况下高可靠容错运行。最后根据仿真和试验结果验证了容错控制策略的稳定性和有效性,以期使导弹电动舵机系统有更高的控制性能。

