基于高阶滑模观测器和改进PLL 的永磁同步电机无传感器控制*
李迎杰 刘旭东
(1.青岛大学自动化学院 青岛 266071;2.青岛大学山东省工业控制技术重点实验室 青岛 266071)
1 引言
近年来,永磁同步电机(Permanent magnet synchronousmotor,PMSM)在电动汽车[1]、风力发电[2]和工业控制[3]等领域得到了广泛的应用,与直流电机和感应电机相比,永磁同步电机具有效率高、功率密度大、结构简单、维修方便等优势[4]。然而在涡轮机、智能机器人等对电机控制性能更高要求的场合,或者在位置传感器安装受到限制的领域,永磁同步电机无位置传感器控制成为了研究的热点[5]。
近年来,模型参考自适应法[6]、卡尔曼滤波法[7]和滑模观测器[8]等方法常用于永磁同步电机的无位置传感器控制,其中滑模观测器法因具有收敛速度快、鲁棒性强等优点被广泛应用,但由于其含有不连续的控制律,因此传统滑模观测器存在固有抖振,进而影响转速估计精度。文献[9]引入了饱和函数代替切换函数,设计了一种改进滑模观测器,并引入自适应律以提高响应速度,削弱了不连续控制律造成的抖振。为了充分抑制一阶滑模由于开关函数的高频切换产生的抖振现象,文献[10]引入高阶滑模算法,根据PMSM 反电动势扩展模型,提出了一种改进Super-twisting 滑模观测器,并引入二阶广义积分器估计反电动势,有效抑制了抖振,提高了估计精度。为解决线性滑模面不能实现有限时间收敛的问题,文献[11]将非奇异终端滑模面引入高阶滑模算法中,提出了一种高阶滑模观测器,实现了有限时间收敛,并提高了反电动势的估计精度。
另一方面,在永磁同步电机无位置传感器控制中,通常采用锁相环(Phase locked loop,PLL)估计转速和转子位置[12],但传统PLL 估计精度较低,可通过引入低通滤波器(Low pass filter,LPF)加以改善,但会导致相位延迟和幅值衰减。为此文献[13]设计了一种自适应正交锁相环(Adaptive quadrature-phase locked loop,AQ-PLL),可实时调整PLL 的带宽,从而改善了转子位置的跟踪性能且避免了相位延迟。扩展状态观测器(Extended state observer,ESO)[14]具有收敛速度快、不依赖准确的数学模型等优点,将其引入PLL 中可提高转速和转子位置的动态跟踪性能,文献[15]根据三阶扩展模型,设计了一种高阶扩展状态观测器,其在参数整定和理论分析方面较为简便,且具有较高的估计精度,但线性扩展状态观测器(Linear extended state observer,LESO)含有线性增益项,不可避免地产生系统抖振。文献[16]基于三阶扩展模型,通过FAL函数设计了一种三阶非线性观测器,减小了系统抖振。
本文基于表贴式永磁同步电机的扩展反电动势模型,通过设计对数滑模面,提出了一种高阶对数滑模观测器,能实现状态变量的有限时间收敛,且有效提高了反电动势的估计精度,抑制了滑模抖振;此外,为了进一步提升锁相环的精度,提出了一种基于 Super-twisting 算法的扩展状态观测器(Super-twisting extended state observer,STESO)来代替锁相环中的PI 调节器,实现了转速和转子位置的精准估计,减小了稳态误差;最后,通过Lyapunov理论证明了该方法的稳定性和有限时间收敛;试验结果表明所设计的无位置传感器控制方法在面对参数失配、突加负载和转速突变时具有较强的鲁棒性,有效提升了系统的动态性能。
2 传统滑模观测器分析
2.1 永磁同步电机的数学模型
对于表贴式永磁同步电机,基于α-β坐标系的PMSM 数学模型表示为[17]
式中,iα、iβ为定子电流在α、β轴的分量;uα、uβ为定子电压在α、β轴的分量;sL为定子电感;Rs为定子电阻;eα、eβ分别为α、β轴反电动势分量,并表示为
式中,fψ为永磁体磁链;eω为电机电角速度;eθ为转子位置角。
将式(1)写为矩阵形式
将式(3)中的反电动势e作为扩展状态变量,则永磁同步电机扩展模型可表示为
2.2 基于扩展模型的传统滑模观测器设计
为了估计电机反电动势,根据式(4),传统滑模观测器可设计为[18]
根据式(5)可得
因此,对不连续的控制律ve取积分即可得到估计的反电动势。由于反电动势中包含着转速和转子位置信息,不连续的控制律导致估计的反电动势存在抖振,继而影响转速和转子位置的估计精度。
由式(5)提出的传统滑模观测器无法抑制符号函数高频切换产生的抖振,所以会影响反电动势的估计精度,且系统状态无法实现有限时间收敛,会影响系统的收敛速度,进而影响系统的动态性能。
3 新型高阶对数滑模观测器设计
为了实现扩展模型滑模观测器的抖振抑制和有限时间收敛,本节提出了一种新型的高阶对数滑模观测器,以实现对电动势的平滑估计。
首先,以电流误差为状态变量,设计对数滑模面为[19]
式中,β>0,k>0,且ln(⋅)为自然对数函数。
设tr为系统从初始状态到达对数滑模面的时间,tf为系统从初始状态收敛于原点邻域范围的时间,则系统状态在对数滑模面上的滑动时间为
式中,li(⋅)为对数积分函数[20]。
证明:当且仅当s=0时,式(7)表示为
选取Lyapunov 函数为
由此表明式(7)提出的对数滑模面是全局渐近稳定的。则式(9)可以表示为
式(11)积分可得
综上,所提出的对数滑模面能实现有限时间收敛,通过增大参数k可以显著缩短系统状态到达原点邻域的时间,有效降低了执行器的饱和风险。
高阶滑模控制律表示为
根据式(7)和式(13),所设计的高阶对数滑模观测器(High-order logarithmic sliding mode observer,HOLnSMO)可表示为
对所提出的高阶对数滑模观测器进行稳定性分析[11],选取Lyapunov函数为
式(15)对时间t求导可得
为了满足 Lyapunov 函数的稳定性条件,Lyapunov 函数的导数必须满足dV/dt< 0。由式(4)和式(14)做差可得误差矩阵方程为[11]
将式(17)代入滑模面式(7),可得
令式(18)等式两边对t求导,并将式(13)代入可得
将式(19)代入式(16)可得
考虑电流误差的微分存在上界,并记为C,即,则式(20)可表示为
由于A12<0,为使式(21)成立,式(14)中的增益参数k1、k2应满足以下条件
因此,满足dV/dt< 0,则高阶对数滑模观测器是有限时间稳定的。所设计的HOLnSMO 框图如图1 所示。
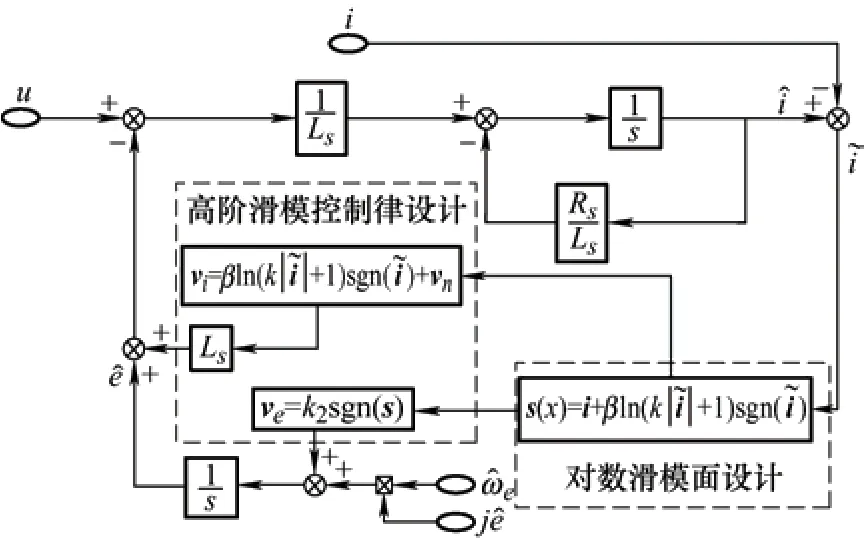
图1 高阶对数滑模观测器系统框图
4 基于STESO 的改进PLL 设计
4.1 传统锁相环
在观测到反电动势信息后,通常采用PLL[21]提取转速和转子位置信息。根据式(2),可得到常规PLL的位置误差为
式中,E s=ψ f ωe;ε为电机位置误差。对式(23)进行归一化处理,当位置误差较小时有
位置误差通过PLL 中的PI 调节器提取转速信息,进而得到转子位置信息。
4.2 Super-twisting 扩展状态观测器
扩展状态观测器因其抗扰性强、不依赖准确的数学模型等优点,广泛应用于永磁同步电机无位置传感器控制中。文献[22]采用ESO 替代了传统锁相环中的PI 调节器,实现了转速和转子位置的精确估计。为了进一步提高转速和转子位置的跟踪精度,提升系统的鲁棒性,提出了一种三阶Super-twisting扩展状态观测器,以消除ESO 中线性增益产生的抖振影响,实现更高性能的控制。
具有参数不确定性的PMSM 动力学模型可表示为
式中,a=pnψ f/J;b=J/B;c=1/J。pn为电机极对数;ψf为永磁体磁链;J为转动惯量;B为阻尼系数;TL为电机负载转矩;Δa、Δb、Δc为参数不确定项,系统动力学的总扰动定义为
将式(26)代入式(25)可以得到
式中,z包含扰动集总项,且假设z在系统动力学中是有界的,由于在电机运行过程中,z的变化缓慢,因此z˙=0,根据式(27)建立系统状态方程
根据式(28)建立三阶STESO
式中,为位置误差;为未知扰动扩展状态的估计值;p1、p2、p3、p4为扩展状态观测器增益。根据式(28)、(29),误差方程表示为
式中,为电角速度误差;为未知扰动误差。
4.3 STESO 的参数设计和整定
STESO 的参数设计决定了改进PLL 的估计性能。在STESO 中,响应时间和鲁棒性是由p3决定的,p3的值越大,响应速度越快,但是,随着p3的增加,转速的超调量和抖振也会随之增加。此外,通过调节p4的值可以保证较高的稳态精度,从而使系统具有较好的动态性能。在保证较好的转速估计性能后,可以再通过调整p1保证转子位置的跟踪性能,p1取值不宜过大,否则会影响收敛速度,此外引入p2能减小稳态误差,但p2的取值应当远小于p1,否则会产生静态误差,影响转子位置的观测精度。可根据文献[23]中提出的规则来调整增益。此外,通过试验,在此基础上对试验参数进行微调,让该方法达到最佳的观测性能。所设计的三阶STESO 系统框图如图2 所示。
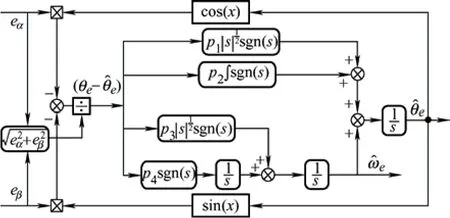
图2 基于三阶STESO 的改进PLL 系统框图
采用所提出的高阶对数滑模观测器代替传统滑模观测器,把三阶Super-twisting 扩展状态观测器引入锁相环,实现了永磁同步电机无位置传感器高性能控制,即提高了转速和转子位置的观测精度,提升了系统的动态性能和鲁棒性。根据上述原理,可设计基于改进滑模观测器和PLL 的永磁同步电机无位置传感器控制,总体系统框图如图3 所示。
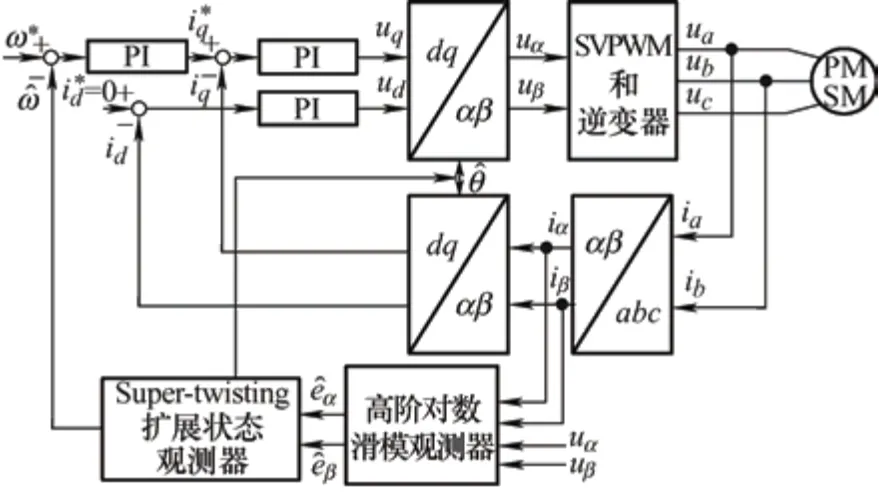
图3 永磁同步电机无位置传感器控制系统框图
5 试验分析
为了验证所提新型无位置传感器控制方法的有效性,本节进行试验验证,试验平台如图4 所示。该试验平台的硬件部分主要包括130 MB 150A 表贴式永磁同步电动机耦合负载电机、逆变器、电机控制专用模块、转矩传感器等。软件部分由Matlab/Simulink和RT-SIM 组成。PMSM 的参数如表1 所示。
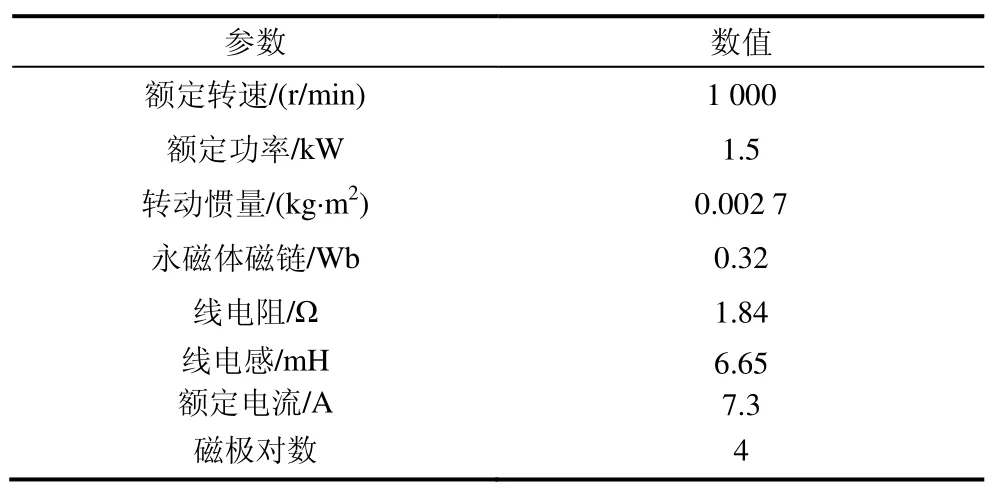
表1 PMSM 标称参数值

图4 永磁同步电机试验平台
首先,为了验证所设计高阶对数滑模观测器的性能性,本节设置了三组观测器的对比试验。第一组为传统滑模观测器(Sliding mode observer,SMO)+锁相环(PLL);第二组为非奇异终端滑模观测器(Nonsingularterminal slidingmodeobservers,NTSMO)[24]+锁相环(PLL);第三组为高阶对数滑模观测器(HOLnSMO)+锁相环(PLL)。其中第一组和第二组为一阶滑模算法,三组观测器参数如表2所示。

表2 试验参数
图5、图6 分别显示了转速为200 r/min、1 000 r/min 时,采用SMO、NTSMO、HOLnSMO得到的α-β轴反电动势波形。由图5、图6 可知,传统SMO 估计的反电动势不够平滑,存在明显的抖振现象。而NTSMO 估计的反电动势虽然平滑程度上有所改善,但仍存在抖振。试验结果表明,所提出的HOLnSMO 能抑制抖振,使反电动势曲线更加平滑。
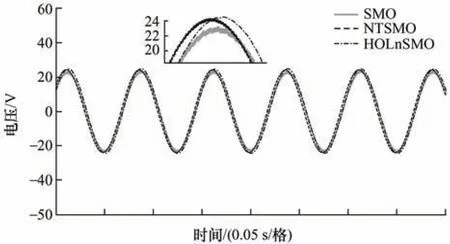
图5 转速为200 r/min 时反电动势曲线
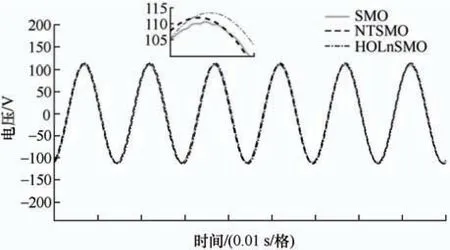
图6 转速为1 000 r/min 时反电动势曲线
参考转速给定值为200 r/min 时,电机实际转速和估计转速曲线如图7 所示,采用传统SMO+PLL、NTSMO+PLL、HOLnSMO+PLL 三种方法估计转速波动分别为9.5 r/min、7.2 r/min、6.5 r/min;电机实际转速波动分别为9.2 r/min、7.4 r/min、5.5 r/min。参考转速给定为1 000 r/min 时,试验结果如图8 所示, 采 用 传 统 SMO+PLL 、 NTSMO+PLL 、HOLnSMO+PLL 的方法估计转速波动分别为8.6 r/min、7.3 r/min、4.3 r/min;电机实际转速波动分别为8.5 r/min、6.8 r/min、4.9 r/min。试验结果表明,采用所设计的HOLnSMO 能有效抑制抖振,提高转速估计精度。

图7 给定转速为200 r/min 时的转速曲线
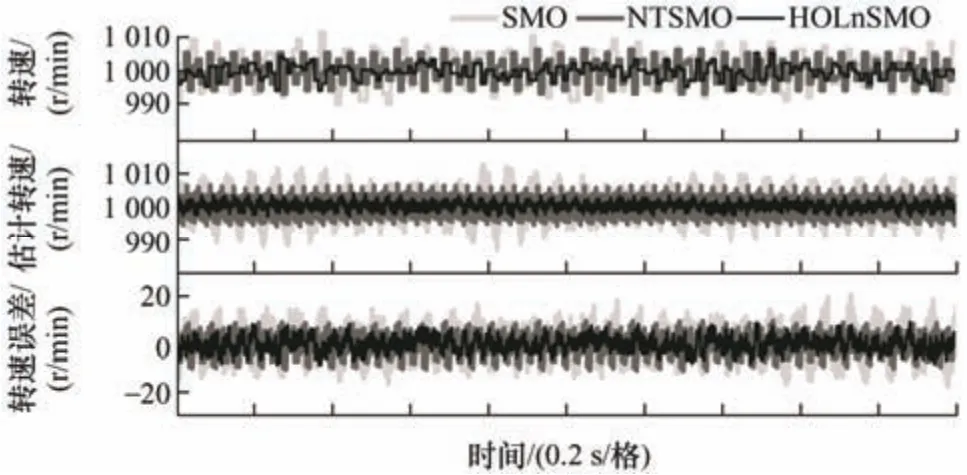
图8 给定转速为1 000 r/min 时的转速曲线
为了验证提升滑模观测器的阶数对系统动态性能的影响,分别采用基于一阶滑模算法的SMO 和NTSMO,与HOLnSMO 做电机升速对照试验。给定转速由200 r/min 突变至600 r/min 时的转速响应曲线如图9 所示。所提出的HOLnSMO 在转速突变时具有较短的响应时间和较小的超调量,且转速稳定后抖振更小。试验结果表明,该方法在应对转速突变时,响应快,超调小,调节时间短,稳态精度高,因此具有较好的动态性能。
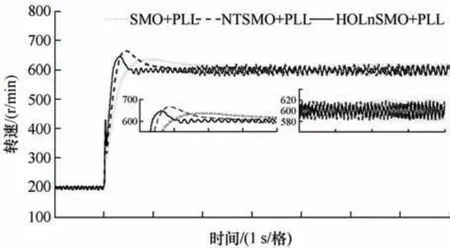
图9 转速突变时的转速响应曲线
其次,为验证所提出的三阶Super-twisting 扩展状态观测器方法的优越性,本节将设置三组对照试验加以分析,第一组为高阶对数滑模观测器(HOLnSMO)+锁相环(PLL),第二组为高阶对数滑模观测器(HOLnSMO)+扩展状态观测器(ESO),第三组为高阶对数滑模观测器(HOLnSMO)+ 三阶Super-twisting 扩展状态观测器(STESO)。三组对比试验中观测器的参数如表2 所示。对于本文所提出的高阶对数滑模观测器,根据式(12)可以得到对数滑模上的参数β和k决定了滑模面的收敛时间,因此β、k的选取要足够大,以保证系统的收敛速度,但参数k值过大会增加系统的抖振。ωf的取值决定了控制律的带宽,通过减小ωf可以减小控制律的抖振,但过小的ωf会降低控制律的带宽,从而导致动态性能下降。
图10、图11 分别为给定转速为200 r/min、1 000 r/min 时电机实际转速响应曲线以及观测器估计转速响应曲线。从图10 中可以观察到,当电机给定 转 速 为 200 r/min 时, HOLnSMO+PLL 、HOLnSMO+ESO、HOLnSMO+STESO 的电机实际转速波动约为5.5 r/min、4.8 r/min、3.6 r/min;估计转速波动约为6.5 r/min、3.6 r/min、2.1 r/min。如图11 所示,当电机给定转速为1 000 r/min 时,以上三种方法得到的电机实际转速波动分别为4.9 r/min、3.6 r/min、2.4 r/min;估计转速波动分别为4.3 r/min、2.1 r/min、0.8 r/min。试验结果表明,与其他2 种方法相比,所提出的HOLnSMO+STESO 策略在不同的给定转速条件下都有更高的转速估计精度。

图10 给定转速为200 r/min 时转速响应曲线
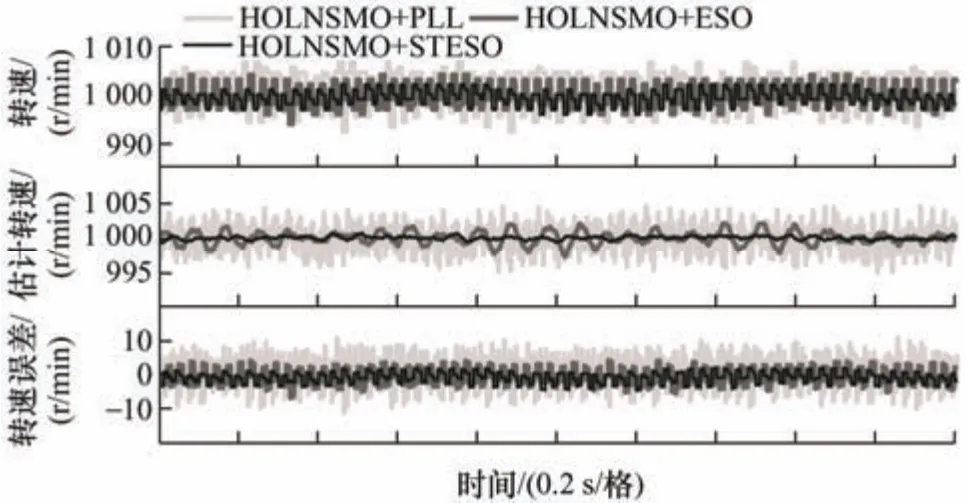
图11 给定转速为1 000 r/min 时转速响应曲线
为了进一步验证所提HOLnSMO+STESO 策略在负载突变时的鲁棒性,设置了两组电机在不同转速下的鲁棒性试验。给定电机初始负载转矩为0.5 N·m,当电机给定转速为200 r/min 时,电机转速稳定后突加1 N·m 的负载扰动,并在5 s 后去除该扰动,转速波动曲线以及转子位置误差曲线如图12a 所示,可得其转速的升降分别为40 r/min 和43 r/min,恢复时间为0.6 s,转子位置误差波动约为0.15 rad。当给定转速为1 000 r/min 时,在相同的时刻突加1 N·m 的负载扰动,也在5 s 后去除该扰动,转速波动曲线和转子位置误差曲线如图12b 所示。可以观察到其转速升降分别为55 r/min 和60 r/min,其恢复时间约为0.9 s,转子位置误差波动约为0.06 rad。此外,图12c、12d 分别给出了给定转速为200 r/min和1 000 r/min 时的d-q轴电流响应曲线。试验结果表明,突加负载扰动时,所设计的观测器仍能准确地估计转速与转子位置信息,具有良好的抗负载扰动能力。
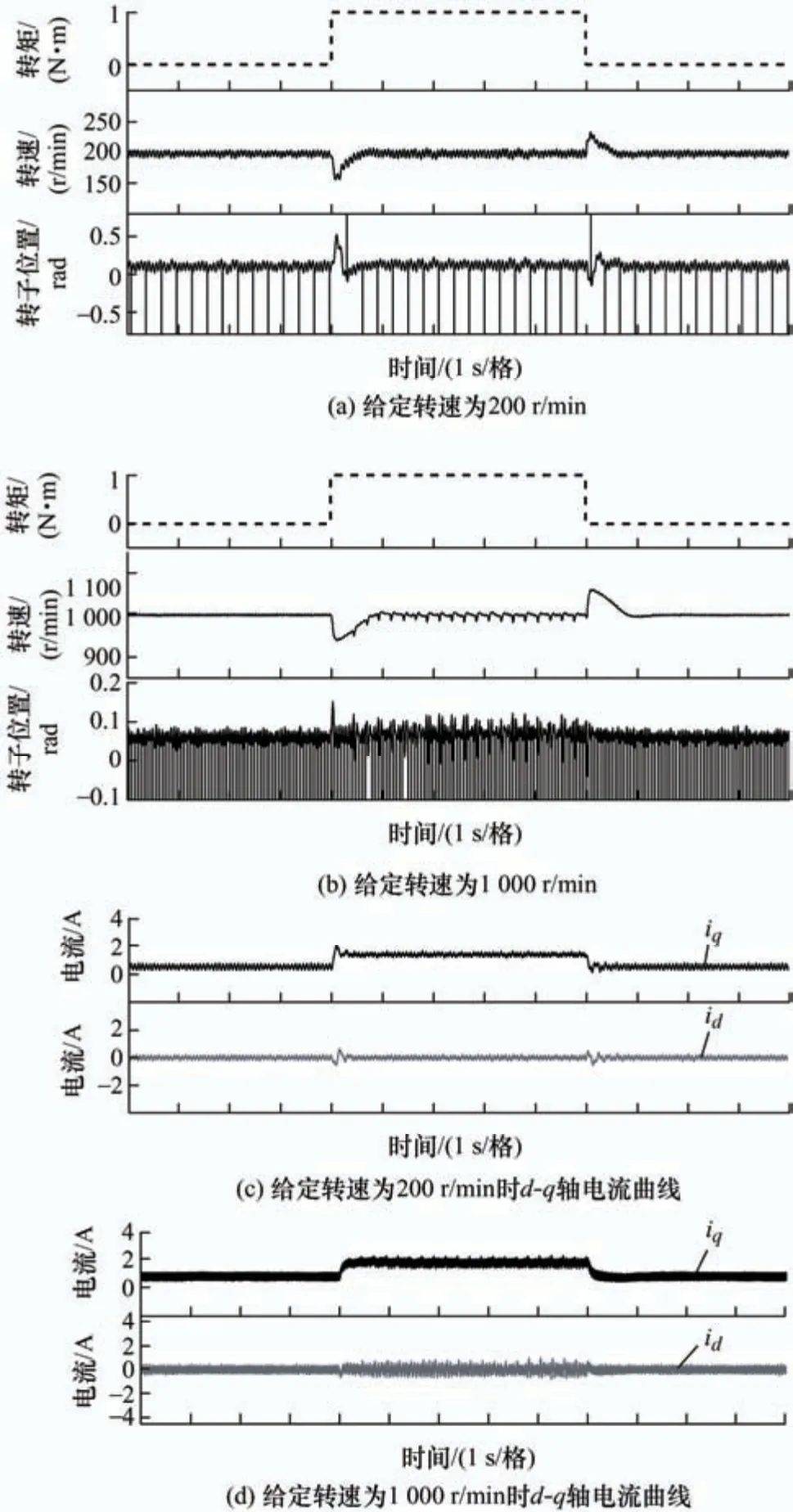
图12 加减载时转速、转子位置误差和电流曲线
为了验证该方法在参数失配情况下的鲁棒性,给定电机参考速度为600 r/min,改变电机参数,假设x=x0(1 +Δx),x=(Rs,Ls),其中x0和Δx分别表示参数的标称值和变化量,电机实际转速和转子位置误差试验结果如图13a 所示。此外,图13b 为参数失配时的d-q轴电流响应曲线。从图13 可以观察到,在参数失配时,HOLnSMO+STESO 策略得到的转速波动较小,且仍具有较高的转子位置跟踪精度,试验结果表明该方法在应对参数失配时具有较强的鲁棒性。
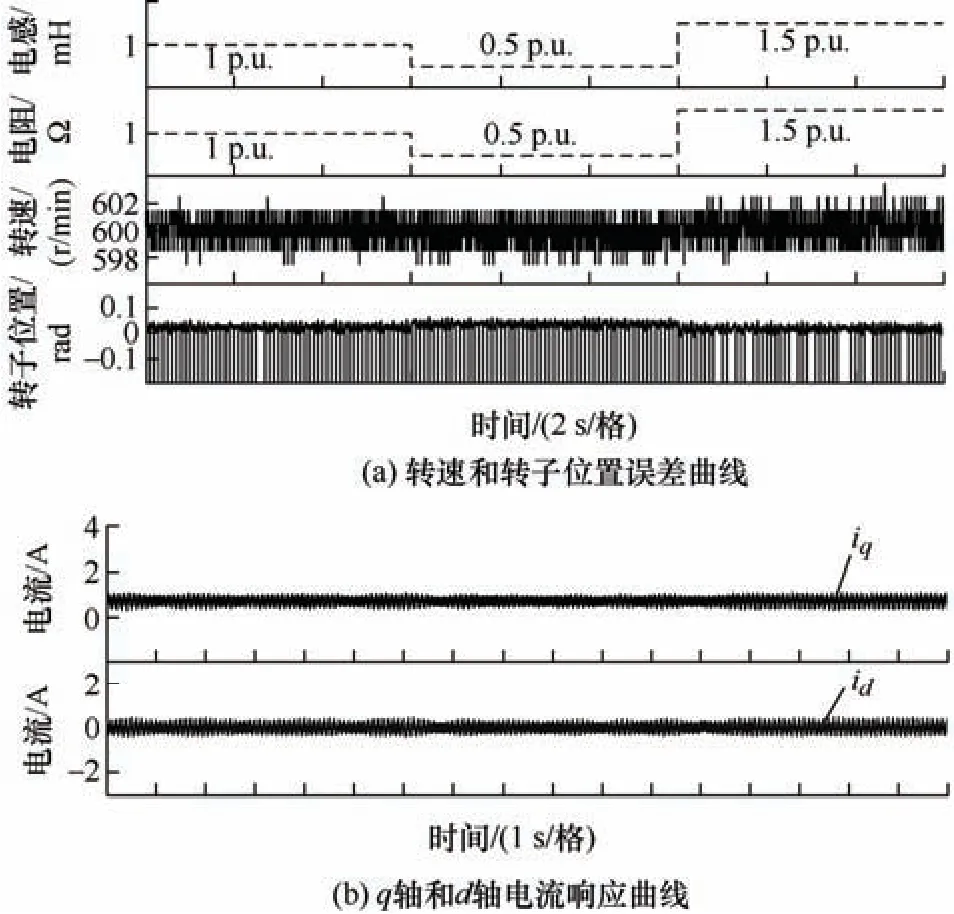
图13 参数失配时转速、转子位置误差和电流曲线
为了验证提升ESO 阶数对系统动态性能的影响,以及所提策略的优越性,引入了一种二阶扩展状态观测器(Second-order extended state observer,2ndorder ESO)[25],与三阶ESO、STESO 做了电机升速的对照试验。电机在0.5 N·m 负载转矩下,给定转速从200 r/min 上升至600 r/min 时,实际转速变化曲线和转子位置误差曲线如图14a所示,d-q轴电流的变化曲线如图14b所示。当转速突变时,2ndorder ESO 的转速超调量较大,转速到达稳态的时间较长,且稳态后的转速和转子位置误差的抖振较大。而本文所提出的STESO 能在保证快速性的同时,拥有较小的转速超调和抖振。试验结果表明,所提方法在应对转速突变时,具有转速响应快、超调量小、稳态精度高等优势,因此表现出了较好的动态性能。
6 结论
本文提出了一种基于高阶对数滑模观测器的永磁同步电机无位置传感器控制方法,并引入了一种新的三阶Super-twisting 扩展状态观测器以提高转速和转子位置的估计精度,通过试验对比分析,得到以下结论。
(1) 根据永磁同步电机反电动势扩展模型,所设计的高阶对数滑模观测器,由于其引入了非奇异对数滑模面,能实现有限时间收敛,且能有效抑制滑模抖振,得到平滑的反电动势信息。
(2) 针对普通锁相环精度差的弊端,设计了三阶Super-twisting 扩展状态观测器对转速和转子位置进行精准估计,提高了观测精度。
(3) 试验表明,所提出的高阶对数滑模观测器和三阶Super-twisting 扩展状态观测器算法,在面对参数失配、突加负载和转速突变等工况时仍具有较好的动态性能和鲁棒性。

