基于改进自适应超螺旋观测器的永磁同步电机无位置控制*

朱国宇 安兴科 诸德宏 陈 前

(1.江苏大学电气信息工程学院 镇江 212013；2.江苏大学汽车工程研究院 镇江 212013)

1 引言

近年来，随着新能源技术的迅猛发展和“双碳”目标的提出，永磁同步电机(Permanent magnet synchronous motor，PMSM)因其高功率密度、高效率和低转矩脉动等优点，在工业控制和生产生活中得到广泛应用。磁场定向控制(Field oriented control，FOC)能够有效地对强耦合且非线性的PMSM 控制系统进行解耦，提高电流控制性能，简化控制器结构并提高系统效率[1-2]。然而，为了实现FOC 控制方法，需要准确获取永磁同步电机转子位置信息。在某些应用环境下，编码器等传统位置传感器存在困难，易受到环境干扰及其他因素影响，同时也会增加系统成本和降低系统可靠性[3]。

因此，为了降低因编码器带来的高成本，并增强系统位置反馈信息的抗干扰能力，PMSM 的无位置控制算法一直是学术界的研究热点。针对电机的不同速度运行范围，无位置控制算法主要可以分为基于高频注入的无位置控制算法和基于反电势的无位置控制算法[4-6]。

基于高频注入的方法主要适用于电机在零速或低速的起动和运行，该方法通过在电机中注入高频信号，并假设电机处于静止状态，通过对电流响应进行滤波分析，进而得到电机的位置信息[7-10]。然而，在实际应用过程中，由于需要采用数模转换器对高频电流信号进行采集和转换，这会增加系统成本。此外，当电机受到转速或负载扰动时，高频注入信号会随之变化，从而影响控制精度。同时，由于高频注入法本身就会产生许多高频噪声，因此在高电流工况下，噪声可能会被进一步放大，从而影响测量精度。

基于反电势的方法则主要应用于中高速场合[11-13]。滑模观测器的方法由于其结构简单、鲁棒性强等优点被广泛应用于电机的无位置控制中[14-15]。然而，滑模观测器中由于符号函数产生的高频抖振现象比较严重，需要采用低通滤波器获得系统的位置信息，这样既增加了运算量，也降低了系统的动态响应能力，同时其造成的相位延迟，也需要进行实时补偿[16-18]。文献[16]提出了一种自适应的滤波器来获取反电势，可以实现更小的相位延迟及更强的动态响应能力。文献[19]使用反正切函数取代开关函数，降低了系统的抖振现象，提高了系统的位置观测精度。除此之外，高阶滑模算法可以将开关函数放入积分项中，无需低通滤波器即可获得反电势的信息，文献[20]采用超螺旋算法对反电势进行观测，并且通过设计可变的滑模增益，使其可以在更大的速度运行范围内使用，然而，超螺旋算法的固定增益在误差较大的观测初始阶段，性能反而不如单纯的线性观测器。文献[21]指出，在速度比较低的时候，电阻、电感误差会对反电势的观测产生一定的影响，进而造成相位延迟。

为了解决上述问题，本文提出一种基于改进自适应超螺旋观测器(Adaptive super twisting observer，ASTO)的无位置控制方法，其能够减小系统抖振现象、提高收敛速度以及自适应地进行电气参数辨识。该方法在超螺旋算法中引入高幂次项，以提高观测器存在一定初始误差时的观测性能，此外通过自适应控制率对电阻参数进行实时辨识，可以有效减少参数误差带来的相位误差。最后，本文通过STM32 的试验平台，对比所提算法与传统滑模观测器以及变增益的超螺旋观测器的性能，验证了所提算法的有效性。

2 PMSM 数学模型建立

为了简化PMSM 的数学模型，假设气隙磁场呈正弦分布，忽略涡流和磁滞损耗，d-q轴电感相同，在α-β轴系下建立电机的数学方程

式中，uα、uβ分别为α、β轴电压；iα、iβ分别为α、β轴电流；Rs为定子电阻；Ls为定子电感，eα、eβ分别为α、β轴反电势，且表示为

式中，ωe为电角速度；θe为电机的电角度，ϕf为永磁体磁链幅值。

3 自适应超螺旋观测器设计

3.1 传统超螺旋观测器设计

超螺旋观测器采用超螺旋算法进行设计，该算法是由一对微分器构成的系统，通过对状态变量进行连续的微分并使用一个稳定的非线性反馈，使得系统能够在快速、平滑的方式下完成跟踪和稳定控制。此外，该算法具有高精度、鲁棒性好等优点，能够解决传统滑模控制中无法避免的抖振问题，由于该算法不受系统的模型误差和外部干扰的影响，因此具有良好的鲁棒性和适应性，并能够应用于复杂的非线性系统中。对于式(1)可以构建如下观测器

式中，上标^表示该物理量的估计值，，sign(·)为符号函数，文献[22]给出了一组参数并作了稳定性证明，定义Δ1为扰动导数的上界，对于本文所设计的观测器，即为当≤Δ1时，选 取 观 测 器 增 益k1=，k2=1.1Δ1可以使系统在有限时间内收敛于真实值。

当反电势估计值趋于实际值后，可以通过反正切或锁相环的方式得出电机的旋转速度以及角度。锁相环结构如图1 所示，通过线性化并选取合适的比例积分(Proportional integral，PI)参数(kp,ki)，估计角度()可以迅速趋近真实角度。而通过反正切函数获取角度和转速信息的方法可由式(5)得到

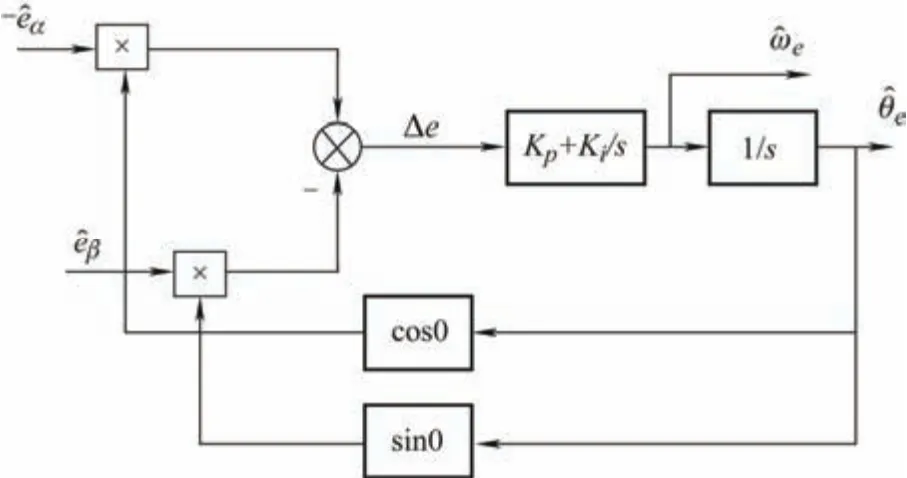
图1 锁相环结构框图

式中，为电角速度估计值。

3.2 参数误差造成的误差分析

考虑电阻以及电感的误差之后，则当电流估计误差为零时，反电势的估计值根据等效控制原理可以得到

式中， ΔR s=Rs0-Rs， ΔLs=Ls0-Ls。下标0 为该物理量的标称值。若假设电机平稳的以电角速度ωe运行，则令xs=xα+jxβ，可以得到如图2 所示的相位图。

图2 反电势误差相位图

从图2 可以看到，参数误差导致的反电势估计误差会引起位置估计的偏差，除此之外，注意到，并且 ΔRs≫ΔLs，那么低速时(小于300 r/min)，考虑电感电阻误差均为50%，定子电流为10 A 时两者造成的误差(电机参数如表1 所示)

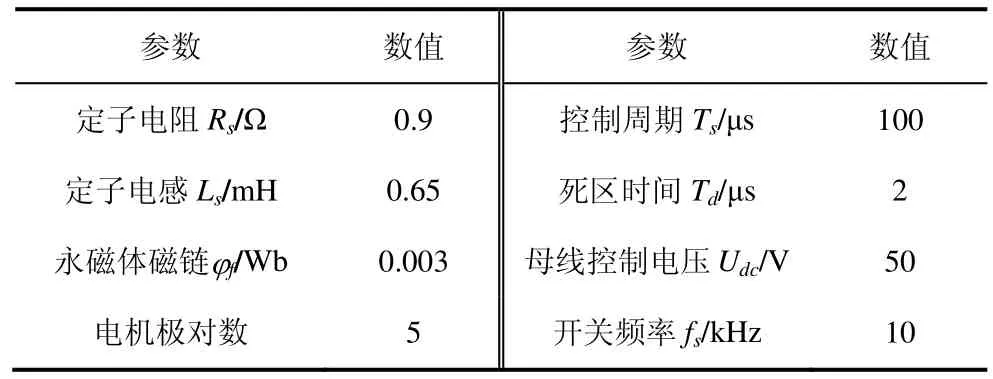
表1 PMSM 及相关参数

可以看出此时电阻误差造成的影响更大，而只有当电机运行速度较高时，ΔLsdis/dt的影响才会更大。其中对于电阻误差造成的相位误差Δδ可以通过矢量的加法运算由式(8)得出

此外，图2 中es与q轴重合，所以，当电机控制策略采用id=0 时，可以看出定子电阻的误差只会使估计反电势的相位不变或增加π，进而本文试验部分验证参数误差的影响时，将id设置为非零值。类似地，在幅值上也会产生误差，进而导致式(5)中计算得到的产生误差。为了改善电机参数误差对于位置估计以及转速估计误差的影响，需要采取参数辨识或者是自适应的方法进行抑制。

3.3 改进的自适应超螺旋观测器设计

虽然超螺旋观测器相较于线性扩展状态观测器(Extended state observer，ESO)具有更强的鲁棒性，但是在误差较大的情况下，前者对于误差的增益会远小于后者，因此此时的收敛速度反而不如ESO。为了改善观测器在跟踪初期的收敛速度，本文在观测器中加入高幂项的同时保持其稳定性，并通过自适应算法对模型参数进行估计，提高位置观测精度。考虑矢量的分解理论，单个矢量最多可以分解为确定的两个方向的矢量，所以在未注入其他频率信号的前提下，本文除了反电势外，选择在低速时对估计误差影响更大的Rs进行辨识，其结构框图如图3所示，并可以表示为

图3 ASTO 结构框图

式中，λ1、λ2、k1、k2为大于零的系数，Rˆs为定子电阻的估计值。

图4 为改进后的控制率与原始控制率关于e的关系图，其中λ1=λ2=1。可以看到，改进后的控制率在误差较小时与改进前基本重合，而当误差增大后，改进后的控制率则是远远大于原方案的。

图4 e-f1(e)关系图

令Δθe为反电势超前定子电流的角度，对于定子电阻Rs的估计，需要做如下假设。

① 电阻误差造成的影响不足以使电机反转，即es-ΔRsiscos(Δθe)>0。

② 定子电流和反电势的相位差小于π/4，即-π/4≤Δθe≤π/4。

对于假设②，电机在低速时通常运行于最大转矩电流比(Maximum torque per amp，MTPA)曲线上，根据式(11)[23]容易得到≤π /4，特别地，对于本文所用的表贴式电机或一些凸极率较低的电机ϑ≈ 0，故在低速时不难满足假设②。

式中，ϑ为电流超前q轴角度，Ld、Lq分别为d、q轴电感。

考虑只有电阻误差的情况，可以得到

当ΔRs<0 时，可以对式(8)进行放缩

而当ΔRs≥0 时，可以得到

由上面的分析可知

式中，k(t)为时变的正系数。可以由比例积分型自适应律表示为

式中，ζi为积分增益。图5 为自适应律估计Rs的结构框图。

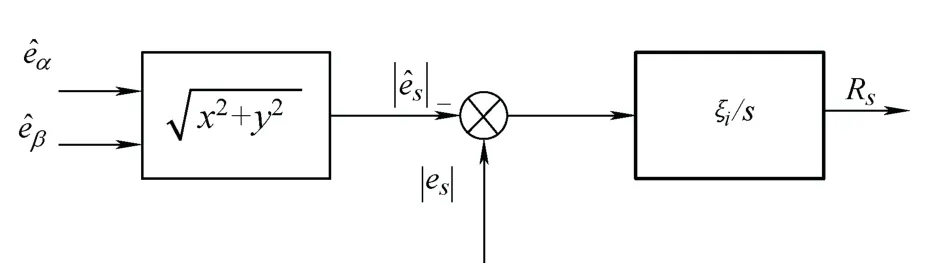
图5 自适应律估计Rs 的结构框图

对于本文所添加的高幂项，利用定时器测量单次电流环执行时间可得，使用传统超螺旋观测器的运行时间为42 μs，而使用改进自适应超螺旋观测器的运行时间为48 μs，仅比原方案多了6 μs，在载频不高的情况下是可接受的。

3.4 稳定性证明

在电机运行过程中，电阻会随着温度的变化而产生一定的变化，但是其变化率相较于观测器带宽而言是相当低的[21]，可以将其导数视为0。

考虑关于Rs的李雅普诺夫函数为

其导数可以表示为

将式(13)代入式(18)可以得到

故所提自适应律可以使定子电阻估计值稳定地收敛于真实值。

考虑关于误差的系统方程，使用式(9)减去式(1)，可以得到

注意到

选择以下李雅普诺夫函数

式中，P=[αij]2×2为对称正定矩阵，可以得到Lα是正定的，对其求导可以得到

式中，Q为对称正定矩阵。 不妨设，可以得到

式中，||·||2为向量的二范数。因此，可以得到

式中，σ1和σ2为正的系数。对式(26)进行放缩可以得到

故选择合适的系数λ1、λ2、k1、k2，即可使观测器跟踪上实际电流，进而观测出反电势。

对于β轴的观测器，考虑到的上界与α轴的情况一致，同理，选择同样的参数可以得到Vβ≥0，且≤ 0。观测器的稳定性就得到了证明。

3.5 系统整体控制方案

系统整体控制框图如图6 所示。首先通过采集电机电流(ia，ib，ic)并使用Clark 变换获取α-β轴系下的电流，接着通过该轴系下的电压指令使用本文所提的ASTO 对反电势以及定子电阻进行估计，此外，根据静止轴系下的电压电流使用递推最小二乘法[24](Recursive least square method，RLSM)对电感值进行测量。接着，通过锁相环得到估计位置和估计转速。通过该估计位置使用Park变换计算得到dq轴系下的电流。此外，对于给定转速(ω*)与估计转速的误差使用PI 控制器获取q轴电流给定(iq*)，接着电流环根据给定电流与实际电流采用PI 控制器输出dq轴电压指令(ud，uq)并转换为α-β轴系下的逆变器电压指令，实现电机控制。

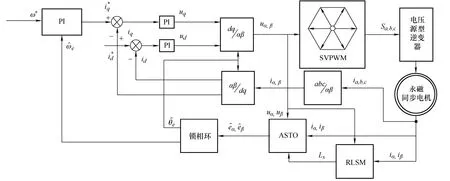
图6 系统整体控制框图

4 仿真及试验验证

4.1 仿真结果及分析

为了验证所提算法的有效性，本文选择传统的SMO 算法[17]、变增益超螺旋观测器(Variable gain STO，VGSTO)[20]作为对比算法。电流环的控制周期为10 kHz，PI 控制器参数为kp=0.6，ki=900。转速环的控制周期为2 kHz，PI 控制器参数为kp=0.08，ki=0.1。传统SMO 算法的滑模增益ksw=1.5，低通滤波器截止频率ωc为1 000 rad/s；VGSTO 算法的参数为σ1=0.04，σ2=0.2；ASTO 算法的参数为k1=19.02，k2=1，λ1=λ2=100(σ1=0.388，σ2=0.001)，ζp=0.1，ζi=1。锁相环的参数为kp=2 000，ki=1 000。电机及相关参数如表1 所示。

为了验证所提算法具有更快的收敛速度，本文选择给定速度为200 r/min，空载运行，且初始角度差为0.4 rad 的情况作为试验及仿真条件。

图7 为三种算法在200 r/min 时的位置估计效果。从图7 可以看到，传统SMO 算法由于对反电势增加了低通滤波器，所以响应速度最慢，并且仍然有一定的抖振现象，然而在加入了更高幂次项后，本文所提的ASTO 收敛速度比VGSTO 的速度更快。

图7 三种算法在200 r/min 时的位置估计仿真结果

进一步地，为了验证算法在电阻参数不准确的情况下的误差，本文设置电阻初始值为0.4 Ω，并且设置id=2 A。图8、图9 为其位置估计误差以及电阻估计曲线，可以看出，随着时间的增加，电阻的估计值在4 s 后趋于真实值0.9 Ω，而位置估计误差随着电阻的变化也逐渐趋于0，其他两个算法的位置估计误差仍然在0.45 rad 左右，但是VGSTO 算法的抖振现象明显更小。

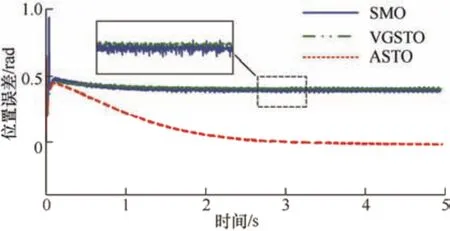
图8 存在电阻误差时分别使用三种算法的位置估计误差仿真结果

图9 ASTO 算法电阻估计值

为了验证算法在高速时的性能以及其抗干扰能力，本文设置给定转速为800 r/min，电阻误差为40%，并在0.5 s 时加上0.5 N·m 的负载转矩，图10、图11为三种算法的位置估计误差以及速度曲线仿真波形。可以看到，在高速时电阻误差带来的估计误差有明显的降低，只有0.1 rad 左右，而ASTO 可以随着时间的增加，对电阻进行估计，进一步减少位置估计误差，在突增负载后，三种算法的估计速度都产生了一个超调，而ASTO 的超调最小，仅有15 r/min，相较于SMO 的120 r/min 和VGSTO 的40 r/min，有了显著的较低。

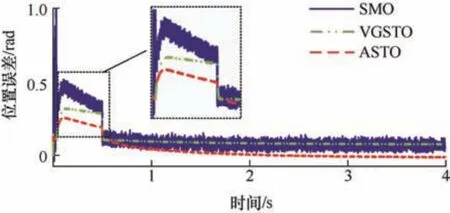
图10 位置估计误差

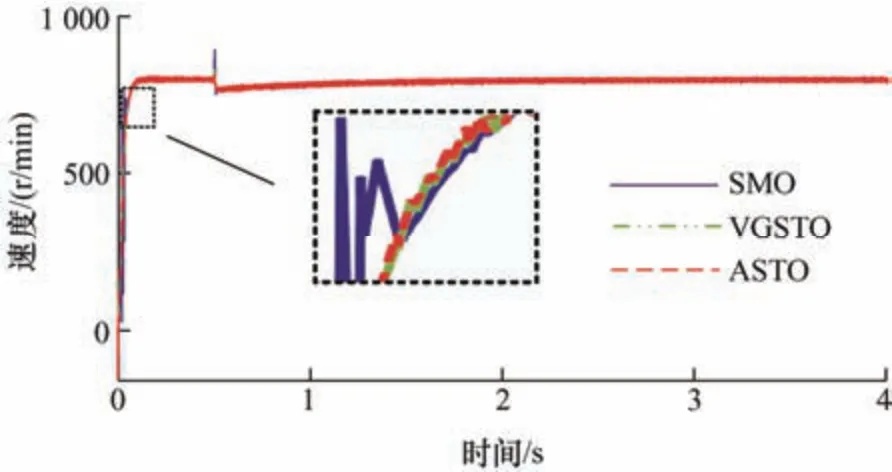
图11 速度估计值

4.2 试验结果及分析

为了验证改进自适应超螺旋观测器的正确性，基于STM32 系统搭建如图12 所示的试验平台。该试验平台包括基于STM32F407 的驱动器、10 kW 电源、永磁同步电机以及计算机。驱动器由六个分立的MOSFET 组成，电机电流通过HCS-LTS3 进行采样，通过模数转换模块输入STM32F407VET6 并进行后续的计算。

图12 永磁同步电机试验平台

图13 为三种算法在0.1 N·m 的初始负载下，运行到200 r/min 时的位置估计误差试验波形。由图13 可以发现，与仿真类似，传统SMO 算法估计速度最慢，在0.4 s 后才基本收敛为0，而VGSTO 和ASTO 的响应速度都更快，前者在0.08 s 收敛到0后，有0.1 rad 的超调，最终在0.8 s 处才基本收敛为0，而ASTO 在0.1 s 时就已经收敛于0 并基本平稳。传统SMO 算法的估计误差抖振现象仍然存在，其均方根(Root mean square，RMS)为0.045，VGSTO与ASTO 的跟踪误差波动明显更小，其RMS 分别为0.029 9 和0.026 6。均方根计算公式为

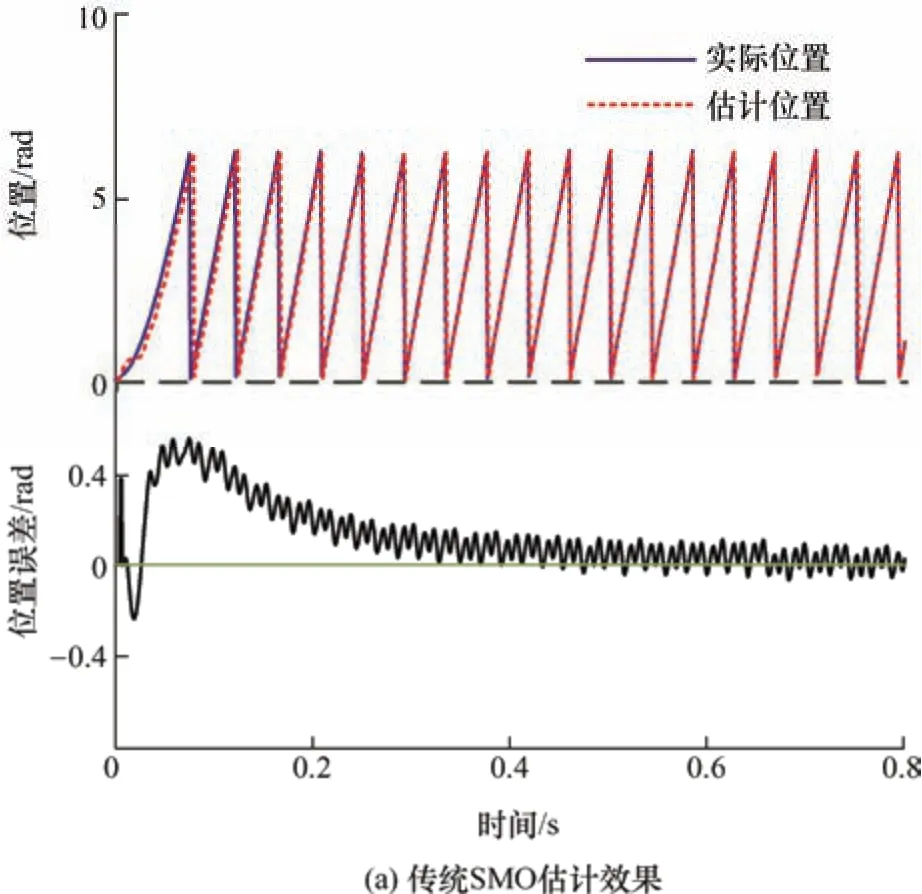
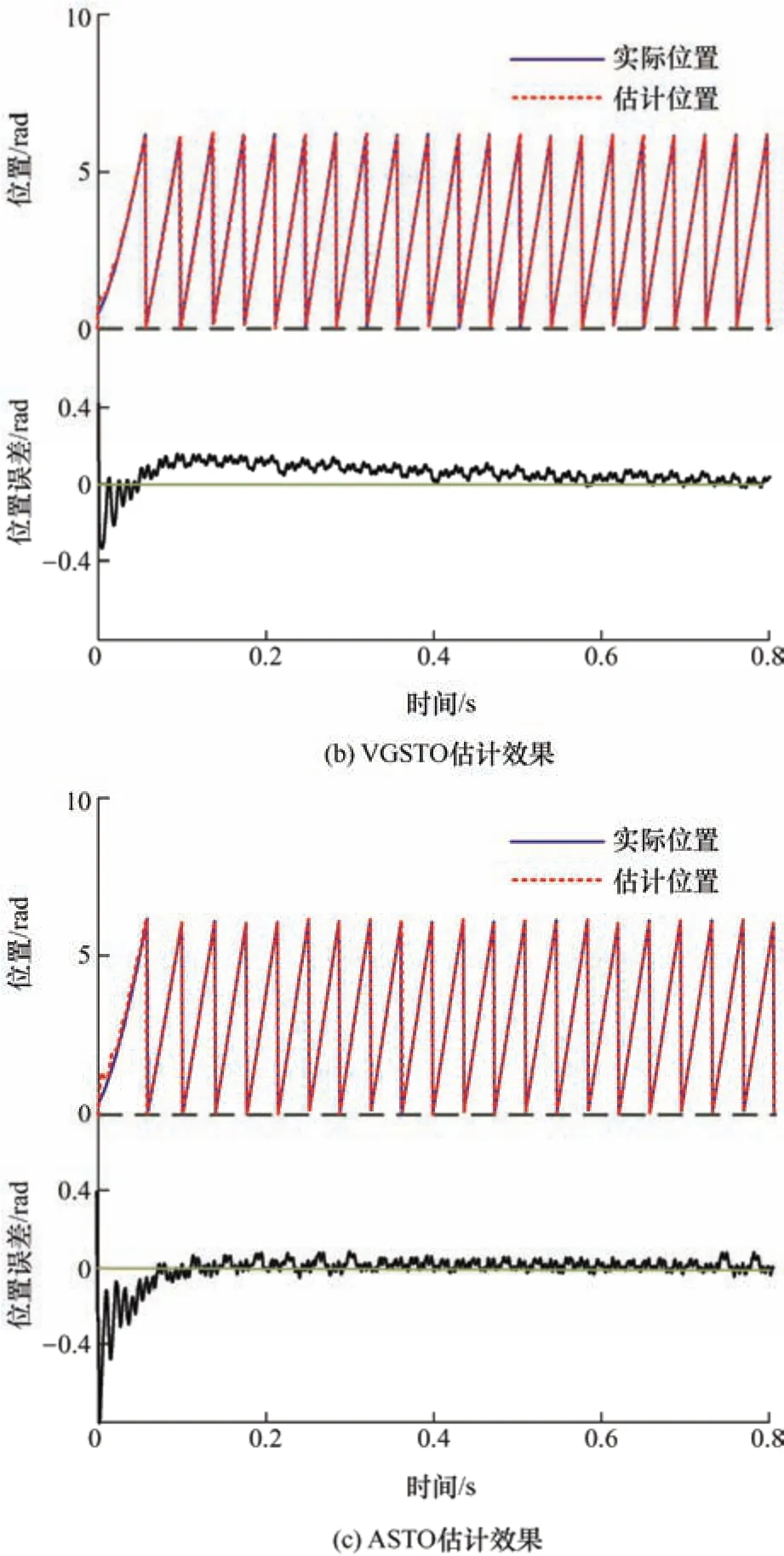
图13 三种算法在200 r/min 时位置估计试验结果

图14、图15 为估计转速误差曲线以及跟踪转速效果。由图14 可以看出，SMO 算法的估计速度在起始阶段有将近60 r/min 的误差，而后两者在该阶段的估计误差只有20 r/min。与位置误差相似，SMO 算法估计速度误差的RMS 为5.08，是其他两个算法的两到三倍，VGSTO 的估计误差RMS 为2.78，而使用ASTO 时的RMS 只有1.88。

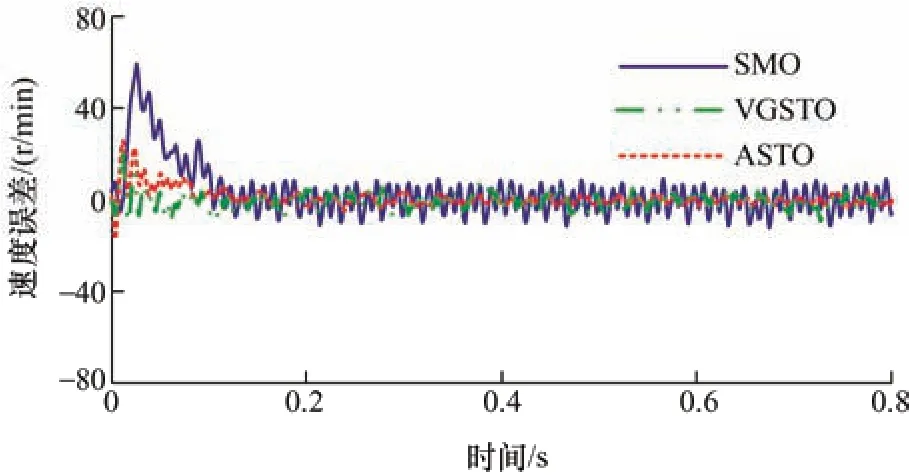
图14 三种算法转速估计误差曲线

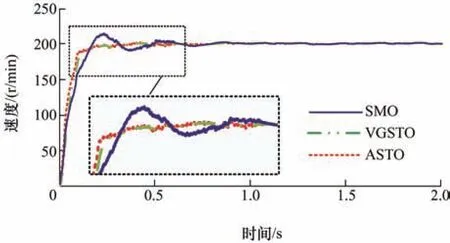
图15 三种算法转速跟踪曲线

考虑电阻误差的影响，设置d轴电流给定为1 A，给定转速为200 r/min，图16、图17 为存在电阻误差时的三种算法位置估计结果以及电阻估计结果。由图16 可以看出，使用SMO 以及VGSTO算法进行位置估计时由于电阻误差的存在，二者均会产生稳态的估计误差，该误差接近0.4 rad，而ASTO 算法会根据反电势的幅值误差对电阻进行估计，从而减少其带来的位置估计误差，图17中可以看出电阻估计值在10 s 后基本稳定在0.93Ω，误差仅在3%，此后位置估计误差也基本维持在0.1 rad 以内。

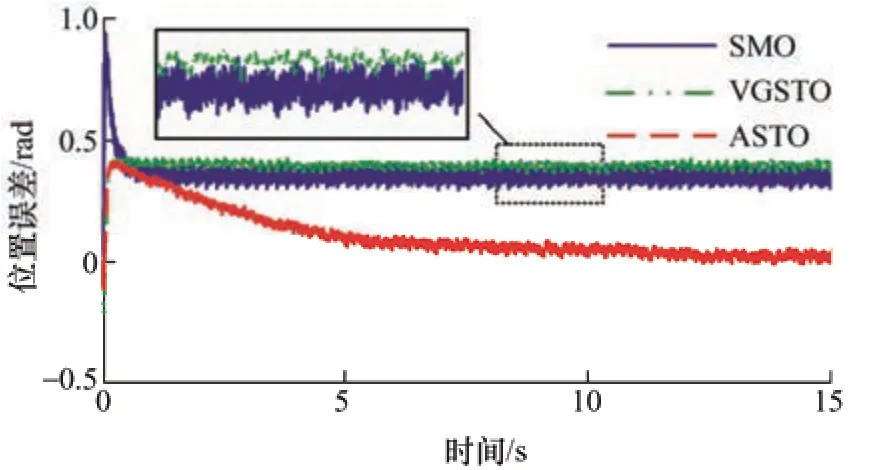
图16 存在电阻误差时三种算法在200 r/min 时的位置估计误差

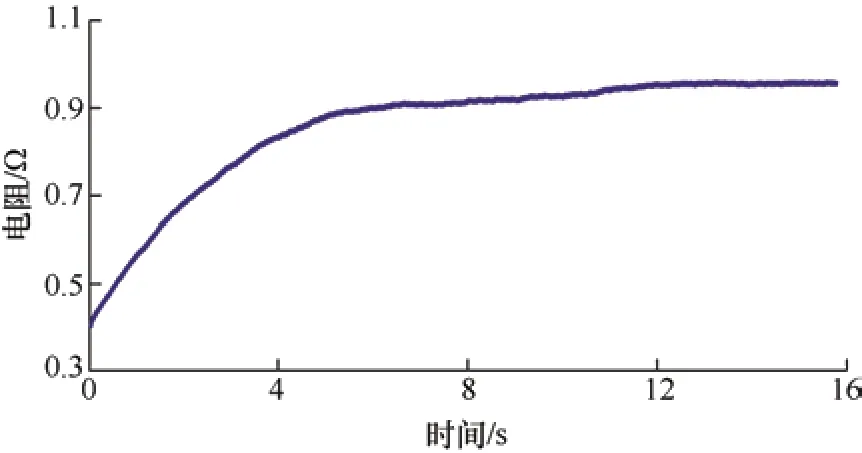
图17 ASTO 电阻估计曲线

作为对比，本文在800 r/min 时增加了一组仿真验证，其中分别设置电感和电阻的误差为50%，图18 为其位置误差波形。由图18 可以看到，当转速提高后，电感误差造成的影响会远大于电阻误差造成的影响。

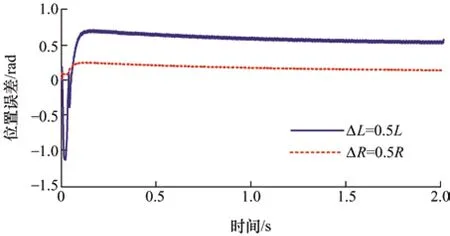
图18 800 r/min 时位置误差仿真结果

而在加入了使用递推最小二乘法辨识[24]电感后的估计位置如图19、图20 所示，可以看到随着电感值逐渐逼近真实值后，位置误差逐渐减小，最终电感误差位置在6%左右，而位置误差最终也仍有接近0.2 rad 的误差。

图19 800 r/min 时加入电感辨识的位置估计误差

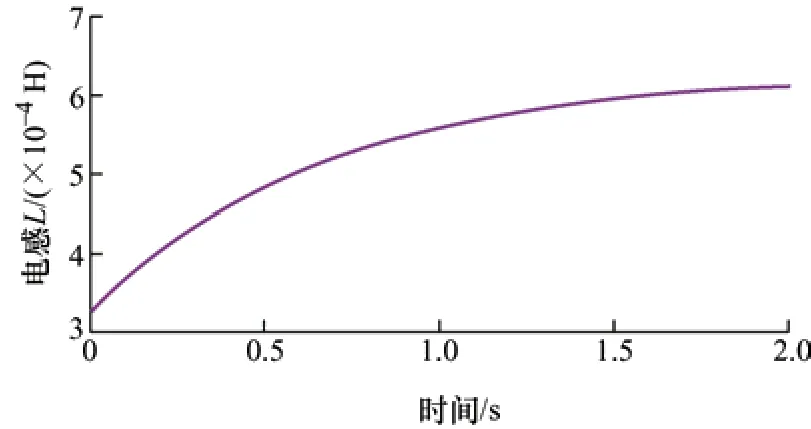
图20 电感辨识曲线

进一步地，为了验证算法在高速时同样具有良好的性能，本文设定给定转速为800 r/min，电阻初始值为0.6 Ω，d轴电流给定为1 A，进行了试验。图21、图22 为其位置估计误差和转速跟踪曲线。SMO 以及VGSTO 在稳定后有0.15 rad 的位置估计误差，而ASTO 仍然可以随着电阻的估计不断减小位置估计误差。SMO 的速度响应曲线有接近180 r/min 的超调，并且响应时间在0.5 ms 左右，而VGSTO 与ASTO 的超调均在30 r/min 左右，响应时间也只有0.2 ms。图23 为其电阻估计曲线，可以看到，速度增大后，电阻估计误差也相应增大到了0.6 Ω，但是误差也可以保持在6%以内，这在高速时对于位置估计的影响已经可以忽略不计。

图21 800 r/min 下三种算法的位置跟踪误差

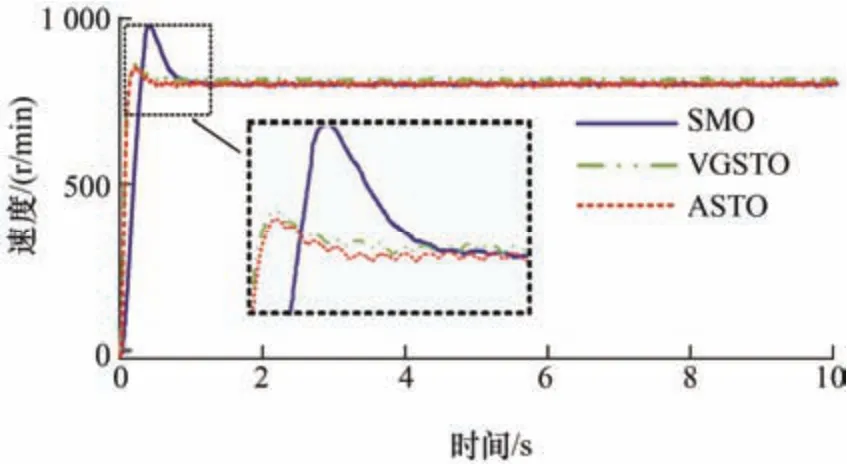
图22 800 r/min 下三种算法的转速跟踪曲线

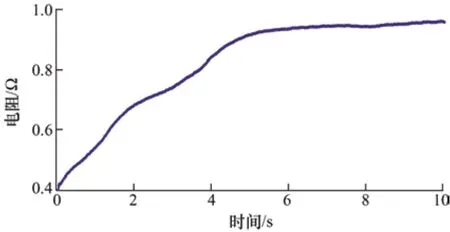
图23 电阻估计曲线

5 结论

为了提高永磁同步电机在低速时的位置估计精度，本文提出了一种改进的自适应超螺旋观测器用于永磁同步电机反电势的估计。通过在低速、中高速，以及有无电阻、电感误差的情况下进行了试验及仿真验证，可以得到如下结论。

(1) 该观测器将传统的超螺旋观测器中加入了新的高幂次非线性项，能够有效提高其在误差较大情况下的收敛速度。

(2) 设计的用于电阻估计的自适应律，可以在电阻误差较大的情况下大大降低电阻误差对角度估计的影响。

(3) 改进观测器较传统方案具有更小的抖振现象、更快的收敛速度以及在电阻存在误差时具有更准确的位置估计性能。