基于可视区域降维的超大规模MIMO 传输性能分析
王 珏,景海涛,高锐锋,施 佺
(1.南通大学 信息科学技术学院,江苏 南通 226019;2.南通大学 交通与土木工程学院,江苏 南通 226019)
随着第五代移动通信系统(5th generationmobile communication technology,5G)的标准化与逐步商用,学术界对下一代移动通信潜在技术的讨论已广泛展开[1]。在5G 三大典型应用场景,即增强移动宽带(enhanced mobile broadband,EMBB)、大规模机器通信(massive machine type of communication,mMTC)及高可靠低时延通信(ultra-reliable low-latency communications,URLLC)的基础上,6G 对宽带传输速率、用户接入密度、通信质量与时延等方面的要求进一步大幅增长。例如,在文献[2-4]中提出,6G 应支持1 000 万台/km2设备的连接密度。现有5G 资源及技术不足以支撑上述新需求,拓展面向6G 系统的新通信资源并开发相应的新型传输技术势在必行。
对于通信资源的拓展可在时域、频域、功率域、空间域等不同维度实现。其中在空间域资源方面,MIMO 技术在4G 开始进入标准,其进一步演进的大规模MIMO 技术也已成为5G 关键技术之一[5]。为应对6G 场景的更高通信需求,期望对空间资源进行更加深入地挖掘。因此,部署更大数量级天线单元的超大规模MIMO(extremely large-scale massive multiple-input multiple-output,XL-MIMO)作为5G 大规模MIMO 的持续演进,已在6G 相关研究中受到广泛关注[6]。其主要应用场景可能包括存在巨量通信节点和通信需求的室内环境(如智慧工厂),或人员分布极端密集的城市区域(如城市CBD 区域)等。
需要注意的是,XL-MIMO 较之于5G 大规模MIMO 并非天线数的简单增加。其不同之处与新的设计挑战主要体现在以下方面:
1)不同的阵列实现形式。较之于5G 大规模MIMO 数十(如64)或百级别(如128)天线量级,XL-MIMO 期望部署天线数可能达到数千甚至更多。此时,考虑风荷载等现实部署约束,其部署形式无法延续过去的集中式阵列形态,而是以分布式形态实现。例如,XL-MIMO 阵列单元可依附于大型建筑表面,因而呈现出超大孔径阵列(extremely large aperture array,ELAA)等新形态。
2)近场与空间非平稳性。由于ELAA 阵列孔径极大,使得部分散射体乃至用户本身可能处于阵列瑞利距离之内[6]。因此,即使对于单一用户,其到XL-MIMO 阵列每一天线单元信道的统计特性可能各不相同,即为信道在阵列域出现空间非平稳。特别地,受遮挡影响,某用户可能仅能“看到”部分ELAA,此即定义为该用户的“可视区域”(visible region,VR);而处于不同位置的用户因面临的遮挡环境不同,在ELAA 上可能具有不同的VR。
3)对低复杂度传输设计的必然需求。对于低开效、低复杂度设计的需求在传统大规模MIMO 中已得到广泛讨论,并已形成许多成熟技术手段如混合预编码[7];但随着硬件成本的降低与算力的提高,全数字大规模MIMO 已可实现,以提供更高的频谱利用率[8]。然而,在XL-MIMO 系统中,由于天线单元数目数量级的增长,在当前硬件限制下,采用全数字架构几乎不可能,因此,低复杂度传输设计成为必然需求。
由前述VR 特性对超大维度的信道进行降维处理,在所得低维信道上进行通信,是XL-MIMO低复杂度传输设计直观且重要的手段,因而在近期研究中得到科研人员的广泛关注,相关研究在信道测量与建模[9-10]、容量分析[11-12]、收发机设计[13-15]、信道估计[16-17]等多方面展开。然而,已有文献多假设简单VR 模型,例如假设多用户VR 固定且已知,并且假设用户VR 外部的阵列天线接收信号能量严格为0。而实际中,该假设很难得到保证。由于电磁波传播的全向性及散射体分布的泛在性,可能存在部分阵列天线接收能量极低(但并非完全为0)的情况。此时,如何定义用户的VR,及不同VR 定义对传输性能有何影响,在文献中尚无分析。
在此背景下,本文展开如下研究:
1)对阵列天线单元接收能量非0 的现实传播场景VR 定义进行了讨论,提出基于绝对能量阈值、相对能量集中度两种VR 判别准则。在XL-MIMO直达径(line of sight,LoS)近场传播模型下,分别对两种判别准则下的VR 统计分布进行了仿真分析。
2)基于所提出的VR 判别准则,首先在两用户场景下分析了最大比传输(maximal ratio transmission,MRT)的可达和速率。在两用户VR 由完全不交叠到完全交叠连续变化的过程中,讨论了可达和速率关于VR 长度或VR 能量集中度、用户位置、系统信噪比(signal-to-noise ratio,SNR)等关键参数的变化趋势,并对其原因加以分析讨论。
3)进一步将讨论扩展至多用户VR 随机分布的场景。选择不同VR 长度将对应不同的信道估计导频开销,进一步影响多用户接入数目。对此时的系统可达和速率进行了仿真分析,进而讨论了最优VR 长度选取以及用户分组优化的可能性。
本文结构安排如下:第1 节描述系统模型;第2节介绍所提出的两种VR 判别准则,并进行仿真分析;第3 节展开基于VR 的MRT 传输性能分析;第4 节总结全文并对未来研究方向进行展望。
1 系统模型
1.1 坐标系与信道模型
考虑如图1 所示的XL-MIMO 阵列。阵列以均匀平面阵(uniform planar array,UPA)的形式部署。阵列共包含M=Mx× Mz个天线单元,分布于如图1 所示坐标系中xoz 所定义平面,且关于z 轴对称布设,阵列下沿高度为H。为方便讨论,假设天线间距在x 方向和z 方向均相同,记为Δ。在所示坐标系下,自阵列左上角起,第mz行、mx列(mz∈{1,…,Mz},mx∈{1,…,Mx})的天线单元所对应的三维笛卡尔坐标表示为

图1 坐标系与系统模型Fig.1 Illustration of coordinate and system model
阵列服务其前方180°范围的扇形区域,区域半径为R。考虑用户配备单天线,且随机分布于该区域内。记用户k 所在方向与x 轴夹角为θk,其与坐标系原点距离为rk,则有θk∈[0,π],rk∈(0,R]。记用户k的三维笛卡尔坐标为ck=(xk,yk,0),则有xk=rk·cos θk,yk=rk·sin θk,且用户k 到第(mz,mx)阵列天线间的距离计算为
其中‖·‖表示Frobenius 范数。考虑无遮挡LoS 传输,任意位置用户到任意阵列天线存在(且仅存在)视距路径,其相应距离可由式(2)计算。考虑简化的自由空间路径损失模型,假设用户发送单位功率,则其在第(mz,mx)阵列天线上的接收功率为
相应地,由XL-MIMO 阵列到用户k 的1 × M维下行信道向量hk可表示为
其中:(·)T表示向量(或矩阵)转置;vec(·)表示矩阵拉直运算。注意式(4)中信道矩阵元素排列顺序与相应XL-MIMO 阵列单元排列顺序一致。在式(4)中,由近场传播造成的各天线单元大尺度路径损耗差异体现于各矩阵元素分母项,而由阵列结构与用户位置联合决定的小尺度信道相移、及其间相关性体现于各矩阵元素分子项。
对式(4)所定义的XL-MIMO 信道向量有如下讨论:1)当用户距离天线阵列足够远(大于阵列的瑞利距离[6]),式中∀mz,mx近似相等。此时,信道向量hk退化为x 与z 两个方向上阵列响应导向矢量的Kronecker 积形式。2)在XL-MIMO 场景下,由于阵列尺寸极大,使得用户极有可能处于阵列近场。此时,式(4)中各对于不同的(mz,mx)天线单元将具有明显不同。因此,hk中各元素能量值具有显著差别(但不存在完全为0 的元素)。如何定义用户VR 以确定其有效使用天线集合,将在第3 节中进行详细探讨。
1.2 VR 定义及其降维信道下的MRT 传输
记式(4)所述信道向量所对应的VR 向量为vk,其定义为与hk同维度的行向量,每一元素值取自{0,1}集合。作为示例,用户k 的VR 向量为
其中:“1”所在位置指明该用户可见的有效天线,即为其VR 区域;“0”所在位置天线对应信道增益极低,因此在传输中加以舍弃;Lk为该用户VR 长度。在该二值化vk定义下,降维的用户信道向量记为
其中,⊙表示向量Hadamard 积。通过该处理,可将信道估计和基带信号处理的维度由M 降至Lk。当Lk< 在大规模MIMO 相关分析中已证明,MRT 传输随天线数增大而渐近趋于最优,因此,本文重点分析XL-MIMO 系统MRT 传输性能。根据式(6)中VR降维信道,相应的MRT 波束成形(列)向量为 其中,(·)H表示向量(或矩阵)共轭转置。此处需要注意的是,虽然的尺寸为M × 1,但其中非零元素仅为Lk。因此,信道信息获取开销及传输运算复杂度可大幅下降。 在式(7)所述波束成形向量下,考虑通过空分多址接入服务K 个用户。此时的系统和速率可写为 其中:P 为发射功率,为方便讨论,此处假设各用户功率分配相同;σ2为噪声方差。 在对式(8)所述系统和速率进行分析之前,首先需对式(6)中的VR 向量vk进行明确定义。具体地,在实际hk各元素均非零时,明确如何对其进行二值化处理,即如何确定示例(5)中所示的0 和1的位置。为此,本文考虑如下两种定义方式: 1)基于绝对能量阈值的VR 判别准则(准则1)。首先,定义所有阵列天线相应信道能量值的最大值为 以此为基准,设定阈值系数κ。在式(4)所示矩阵中,将所有满足 相应(mz,mx)位置处的元素置1,其余置0。 2)基于相对能量集中度的VR 判别准则(准则2)。计算全部阵列天线信道能量值之和为 以此为基准,设定能量集中度系数η。将所有阵列天线信道能量值从大到小顺序排列,并从起始位开始叠加,直至叠加能量值大于停止。此时在式(4)所示矩阵中,将已叠加(mz,mx)位置处的元素置1,其余置0。值为1 的元素数目即为此时所判定的VR 长度Lk。 在准则2 下,进一步定义用户k 所对应的阵列能量集中指数∊k。在所述判别准则下,即比例为Lk/M的天线单元集中了比例为η 的总能量。因此,定义 考虑极端场景,当阵列能量完全均匀分布,此时Lk=ηM,相应∊k=0;当Lk=1,即一个天线单元上集中了所需η 比例的全部能量,此时∊k=1;在上述极端场景的中间部分,∊k值越大,表明用户k 所处位置在阵列上的能量集中度越强,即所表现出的空间非平稳性越明显。越大的∊k对于利用VR 的简化传输设计越有利。 在实际系统设计中,可根据需求灵活选择VR判别准则。因为本文重点考虑MRT 传输方案,此时,考虑所有参与通信的天线集合总能量更具意义。在以下分析中,将以VR 判别准则2 为主展开讨论。 考虑第1 节所述用户分布场景,对上述判别准则下的VR 分布情况进行仿真分析。在下文的仿真中,定义参数如下:Mx=20,Mz=50,因此XL-MIMO阵列天线单元总数为M=Mx× Mz=1 000。考虑XL-MIMO 阵列依附于大型建筑物表面,不失一般性,在x 与z 两个阵列方向设置同等的较大天线间距Δ=1 m,与载波波长无关。 在此参数设置下,首先对典型位置处用户在整个XL-MIMO 阵列上的信道能量连续分布进行直观展示与比较。分别选取θk=0,π/2,π,rk=20,100,500 m 共9 个典型位置,画出相应位置用户在阵列上的能量分布(dB)如图2 所示。需要注意的是,图2为在理想信道模型下仿真获得,仅为反映不同位置用户在天线阵列上的能量分布差异(图中黄色部分对应阵列上的能量集中处),其绝对数值并无实际意义。 图2 不同位置用户的XL-MIMO 阵列能量分布比较Fig.2 Comparison of antenna array energy distribution in different locations 观察图2 可得到以下重要启示和结论: 1)首先,在XL-MIMO 阵列尺寸下,不同位置处的用户在阵列上的能量分布明显不同,这为基于VR 的信道降维及选择VR 正交用户进行低复杂度传输提供了现实基础。但值得注意的是,能量在阵列上呈现连续变化,并不存在接收能量严格为0 的阵列天线单元。因此,如何将该连续能量分布图进行二值化处理,并由此确定各用户VR 区域,对于后续传输设计具有重要意义。 2)不同角度用户的阵列能量集中程度受到其距离阵列距离的显著影响。具体而言,当用户位于阵列较近的位置时,不同角度用户VR 差异并不明显(如图2(a—c)所示)。这是因为此时用户距离低处阵列每一天线单元的距离均处于 较小量级,因此由式(3)所得能量差异并不显著,均集中于阵列的下半部分。随用户到阵列的距离变远(rk增大),用户VR 关于角度的变化趋于显著(如图2(d—i)所示)。 3)当rk进一步增大时(如图2(g—i)所示),各用户VR 在角度域变得更显著,而在阵列纵向方向(即图1 中z 轴方向)变得不再显著。这是因为在该仿真场景设置下,在阵列边缘位置处(如图2(g—i)所示),用户到阵列x 方向天线单元的距离差异大于其到阵列z 方向天线单元的距离差异。换言之,随用户距离变远,可认为用户已处于其“可视”子阵列的远场,但仍处于整体阵列的近场。由此产生用户能量在其“可视”子阵列上能量分布差异不大,但在整体阵列上能量分布仍有差异的结果。 由图2 所示直观结果进一步归纳出如下关于多用户VR 在阵列上空间分布的结论:根据用户距离阵列的远近,可将其VR 分布归类为几个典型区域。在距离阵列较近的区域,多用户VR 区别主要体现在阵列的上、下部分(即z 轴方向)。注意到在图2仿真中假设用户均分布于地面,因此VR 集中在阵列上部的情况并未画出。在城市场景中,当用户分布于建筑物高楼层,垂直方向的VR 区别将有明显体现;在距离阵列较远的区域,多用户VR 区别主要体现在阵列的左、右部分(即x 轴方向);在上述两区域的中间区域,多用户VR 区别将同时体现在x 与z两个方向。 需要注意的是,尽管在图2(g—i)仿真图像中显示了阵列不同部分接收能量的相对差异,但随着用户距离变远,其位置趋于整体阵列的远场,阵列单元能量绝对差异值因而减小。该趋势由图3 所示的阵列单元接收能量柱状图分布可清晰显示。在图3 中,选取图2(a),(d)和(g)所示的3 组仿真参数设置,分别画出相应所有阵列天线接收能量绝对值(排序后)的柱状图分布。如图所示,当rk越小时,其阵列天线能量绝对差异越加显著。 图3 不同距离下的阵列天线能量绝对值柱状图分布Fig.3 Distribution of antenna array energy absolute at different distance 对于图3 所示的3 个场景,分别基于2.1 节所述VR 判别准则2 对其阵列能量连续分布进行二值化处理。选取η=0.5,即集中阵列总能量50%的天线集合作为其有效VR,所得结果见图4。在图4 所示的3 个场景下,随着rk由小变大,所对应的判定VR 长度Lk分别为345,435,490。相应地,式(12)所定义的能量集中指数∊k分别计算为0.059,0.022,0.003。观察数据变化规律可知,随着rk增大,阵列能量分布趋于平均;特别地,对于rk=500 m,图3(c)所示能量分布柱状图趋于平稳,此时约有一半的阵列天线(490/1 000)集中了η=0.5 的阵列总能量,其相应∊k=0.03 亦趋近于0。需要注意的是,在考虑的LoS 传播场景下,即使处于阵列近场(如rk=20 m),其对应的能量集中指数仍较低。当进一步考虑传播中的遮挡等现实因素影响,可期望更大的∊k,及对VR 更有效的利用。 图4 不同位置用户的二值化VR 区域Fig.4 Binarized VR region of the users in different locations 最后,对所述场景下待覆盖区域内∊k的总体分布情况进行仿真,并讨论其关于系统参数的变化。在图5 中,考虑用户均匀分布于θk∈[0,π],rk∈(0,500]所描述的区域。考虑两种不同阵列高度H=20,50 m,及3 种不同阵列天线间距Δ=1,2,3 m。其余参数设置如无另外描述,均与2.2 节开头所述相同。在随机生成的用户位置处,通过式(12)计算所得的∊k值亦为随机变量。统计画出其在不同参数下的累积概率分布函数(cumulative distribution function,CDF)曲线如图5 所示。由图可见,随阵列高度H 降低或天线间距Δ 增加,图中CDF 曲线右移,意味着在随机用户位置处出现更大∊k的概率增大;换言之,更多用户将具有更高的阵列能量集中度,对应于更小的VR。这是因为对于固定的待覆盖区域,随着H 降低或Δ 增加,更多用户将处于阵列的近场。在LoS传播环境下,这对于后续利用VR 的低复杂度传输设计是有利的。 图5 随机用户分布下的阵列能量集中度指数CDF 曲线(固定η=0.5)Fig.5 CDF of antenna array energy concentration under random user distribution(fixed η=0.5) 从以上仿真可以看出,在随机用户分布场景下,存在用户位置可以取得较大的∊k。特别地,当H=0 m 时,所考虑仿真场景下的随机值最大可达到1,意味着在此时的相应位置,1 根天线上可集中超过50%的阵列能量。接下来,下文将继续讨论如何选取阵列能量集中度足够大的用户进行传输设计。 本节对基于VR 的MRT 传输性能进行分析讨论。为重点关注用户空间信道VR 交叠对传输性能的影响,在分析中忽略各用户信道中的路径损耗因素,对用户信道进行如下归一化处理: 相应地,在式(6)与式(8)计算中,hk均以代替。 首先对基于VR 进行降维MRT 传输可能造成的影响进行简要讨论:需要注意的是,除易见的降低计算复杂度与系统开销方面的优势外,降维MRT传输存在用户有效信号能量减少与用户间干扰信号能量减少之间的权衡。举例而言,考虑用户1 与用户2 具有近似正交的VR。当选择部分阵列天线对用户1 进行传输时,其有效信号能量较之于使用全部阵列天线进行传输将降低;但与此同时,可避免使用其VR 外阵列天线进行传输时对用户2 的干扰,相应可能使用户2 的可达速率得以提高。考虑该权衡关系,应存在最优的VR 长度选择,使两用户可达和速率得到最大化。 首先从两用户场景出发,对上述讨论进行详细分析。在仿真中设置H=50 m,Δ=1 m。作为示例,考虑在角度域分离的两用户,假设两用户角度分别设定为θ1=0,θ2=π,且其到原点距离相同为r。考虑近、远两个典型场景(r=20,500 m),并考虑在判定各用户VR 时选取不同的能量集中度系数η,在图6 中分别仿真给出两用户和速率、以及用户1 的有用信号强度值、受到用户2 的干扰强度值等指标关于η 的变化曲线(由于两用户对称部署,用户2所对应的信道、干扰强度值变化趋势类似,因此在图中不再重复画出)。 图6 两用户和速率(左轴)与信号/干扰强度(右轴)关于η 设置值的变化Fig.6 Sum rate(left)and signal/interference strength(right)vs.η for two users 首先,如图6(a)所示,随着η 数值设定增大,意味着对各用户而言,均会有更多阵列天线单元被判定为其VR。相应地,其有用信号能量关于η 单调增加。另一方面,随用户2 VR 判定区域的增大,其对用户1 的干扰也呈现整体增强的趋势。但由于两用户信道相位不同且随机叠加,干扰强度关于η 呈现波动增加的趋势。两者共同造成可达和速率的波动变化。存在最优的η 设定使信号与干扰强度之间的权衡达到最优,即使得和速率最大化。该最优η 的取值与系统信噪比、用户位置、阵列天线数目等多项参数有关。 更具体而言,最优η 的选择受到系统信噪比的重要影响。在低信噪比下,系统工作于噪声受限区域。此时干扰造成的影响可忽略,为使和速率最大化,倾向于提高有用信号能量。因此,图中RSN=-2 dB所对应的和速率曲线关于η 单调增加。随着信噪比的增加(如图RSN=2,5 dB 曲线所示),用户间干扰的影响变得不可忽略。此时,最优η 取值明显减小。系统以降低有用信号强度为代价,换取用户间干扰的大幅降低,最终实现可达和速率的提高。此外,值得注意的是,由于XL-MIMO 天线数目巨大,系统可达和速率关于信噪比增加将迅速达到饱和状态。例如,对于RSN分别为2,5 dB,当η 增大时,系统可达和速率饱和至同样数值。 当两用户到阵列距离增大(r=500 m),上述结论在图6(b)中可得到类似观察确认。值得注意的是,当η 取值较小(约η <0.4),两用户之间的干扰强度趋近于0。该现象可由图4 中的VR 判定结果来解释。比较图4(a)与图4(c),可见远距离处的两用户在VR 域的分离更加明显,且当η 取值较小时能完全正交,因此,可大幅降低此时的用户间干扰强度值。相应地,较高信噪比下使得和速率最大化的η值设定也可在此区域取得。需要注意的是,因为在进行速率分析时对信道进行了归一化处理,忽略其路径损耗的影响,图6(b)中的最大可达和速率由于可实现更低的干扰,反而比图6(a)中可达和速率更高。 在3.1 节中,重点讨论了固定用户数目、位置场景下利用VR 进行降维MRT 传输在有用信号与干扰能量权衡控制方面的潜在优势。在本节中,进一步对其在系统开销方面的优势进行初步讨论。系统开销与实现复杂度需要综合考虑硬件成本、算力、可用时频资源、通信协议、信道估计与传输算法等众多因素的影响,难以全面精确描述,因此,本节考虑最简化的玩具模型(toy model)来探讨VR 降维设计在系统开销方面的影响。考虑如下最基本的开销方面的权衡关系:当用户信道维度得以由M 大幅降低为Lk(判定的VR 长度),在有限的资源和开销下,系统应有能力服务于更多用户。为便于讨论,假定所有用户判定VR 长度统一为Lk=L,∀k,则系统总服务用户数K 与L 成反比例关系为 以下就VR 降低开销对系统性能的影响进行讨论。考虑与图5 仿真同样的系统参数及用户分布区域(H=50 m,Δ=1,3 m,R=500 m)。忽略用户调度的影响,即每次用户选择在目标区域内随机选取K 个用户进行传输。对于每个固定K 值,仿真随机进行1 000 次用户选择并计算其相应可达和速率。基于此数据,分别画出系统平均和速率关于L 的变化曲线,及典型L 设置下随机和速率的CDF 分布曲线,如图7、8 所示。仿真中均设置=1 000,即当用户选择使用全部阵列天线,则系统开销与复杂度限制仅可支持单用户传输。随着L 减小(即VR 判定时所要求的能量集中系数η 值减小),可服务的用户数目增多,但同时会造成更大的用户间干扰。 图7 多用户平均和速率关于VR 长度L 的变化Fig.7 Average sum rate vs.L for multi-user 观察图7 可得出如下重要结论: 1)在多用户传输场景下,存在最优的L 取值,使系统可达平均和速率最大化。如图所示,随着天线间距Δ 增大,该最优取值趋于减小。就图中示例而言,Δ=1 m 时所对应的最优L 值在200 左右;而Δ=3 m 时对应的最优值L 约为100。这是因为,更大的Δ 对应于更明显的空间非平稳性及在阵列上更为集中的能量分布(在图5 中已验证该结论)。此时,总体上各用户可设置更小尺寸的VR 区域,服务更多用户,但不会对有用信号能量和干扰能量产生明显影响。 2)可以看到,在L 较小的区域,由于同时服务的用户数增多,用户间干扰增大,实际工作在干扰受限区域。因此,在此区域内,不同信噪比所对应的可达和速率曲线趋于重合。另一方面,在图示右半部分L 较大的区域,随着L 缓慢增加,速率曲线趋于平稳。这是因为在此仿真设置下,该区域内实际均对应于单用户传输,速率的缓慢增加仅来源于L增大而带来的有效能量提升。 3)当Δ 为3 m 时的可达和速率普遍高于Δ 为1 m 时的速率。这意味着在VR 降维的XL-MIMO传输中,更为明显的空间非平稳特性(对应于图5中分布更广的∊k)往往是更加有益的。 最后,为了对多用户可达和速率的随机分布进行更为全面的分析与展现,固定Δ=1 m,RSN=5 dB,并分别选取L=20,200,1 000 3 组典型参数设置,绘制可达和速率随机分布的CDF 曲线如图8 所示。较之于最优VR 长度设置L=200,其他两组设置下的CDF 曲线较陡,近似于直线。这是因为当L=20 时,每次随机选择用户数目较多(10 个),因此各次选择在统计意义上差别不大;另一方面,当L=1 000时,每次仅随机选择一个用户。又因为在计算速率时对信道进行了归一化处理,因此各次选择所能达到的波束成形可达和速率完全相同。值得注意的是,在L=200 的设置下,CDF 曲线分布较宽,意味着不同的用户选择对实际可达和速率有显著影响。特别地,与有限维MIMO 不同[18-19],此时若选择了不适当的用户成组传输(如曲线左端拖尾部分),其可达和速率甚至可能低于单用户波束成形可达和速率。该结果表明,用户选择与调度是VR 降维XL-MIMO 传输中需要深入研究的重要方向。 图8 随机分组多用户传输下的可达和速率CDF 曲线Fig.8 CDF of achievable sum rate under random group multi-user transmission 本文基于VR 降维的XL-MIMO 传输性能展开研究,得到以下结论。 1)实际传播环境中用户在XL-MIMO 阵列上的能量往往呈现出连续分布特征,如何确定用户的二值化VR区域取决于所采用的判定准则。 2)提出基于绝对能量阈值与基于相对能量集中度的两种VR 判定准则。在实际处理中,应根据系统特性及传输要求选取特定的判定准则。 3)在LoS 传播环境下,用户VR 的能量集中度与用户所在位置有关。当用户与x 轴夹角越小,且用户距离阵列越近,其能量集中度越大;另一方面,不同用户VR 分离程度亦与其位置有关。一般而言,在同等能量集中度下,当用户距离阵列越远,其在角度域的VR 分离程度越大。 4)VR 降维MRT 传输的潜在性能增益来源于以下方面:通过选取阵列的不同部分天线集合对不同用户传输,可以取得有用信号能量与干扰强度之间的最优权衡;同时,在给定的系统开销和复杂度下,可以服务更多用户,取得多用户复用增益。根据系统和环境参数设置的不同,存在最优的VR 判定系数选择。 面向6G 的XL-MIMO 相关研究工作正在受到越来越多科研人员的关注,根据本文讨论,在以下方向仍有待于开展深入研究: 1)存在遮挡及散射的一般传播环境下的VR统计特性分析; 2)在VR 场景下,更多预编码方案如迫零、最小均方误差预编码在实际复杂度与系统开销约束下的传输速率性能分析及优化设计; 3)在推导基于VR 的传输速率解析表达式基础上,对最优VR 判定准则及VR 长度设置等相关参数进一步优化设计; 4)基于VR 的多用户选择成组及调度方案优化设计。2 VR 判别准则及分析
2.1 基于绝对能量阈值和相对能量集中度的VR判别准则
2.2 LoS 场景下的阵列能量分布与VR 判别仿真分析
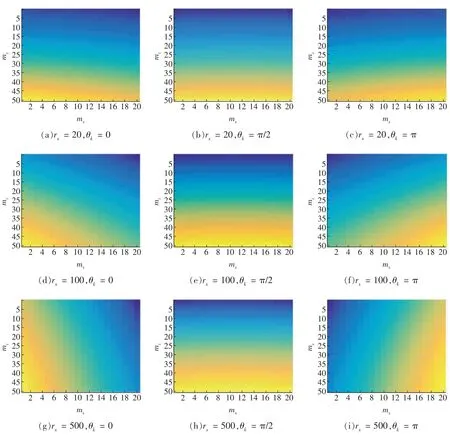
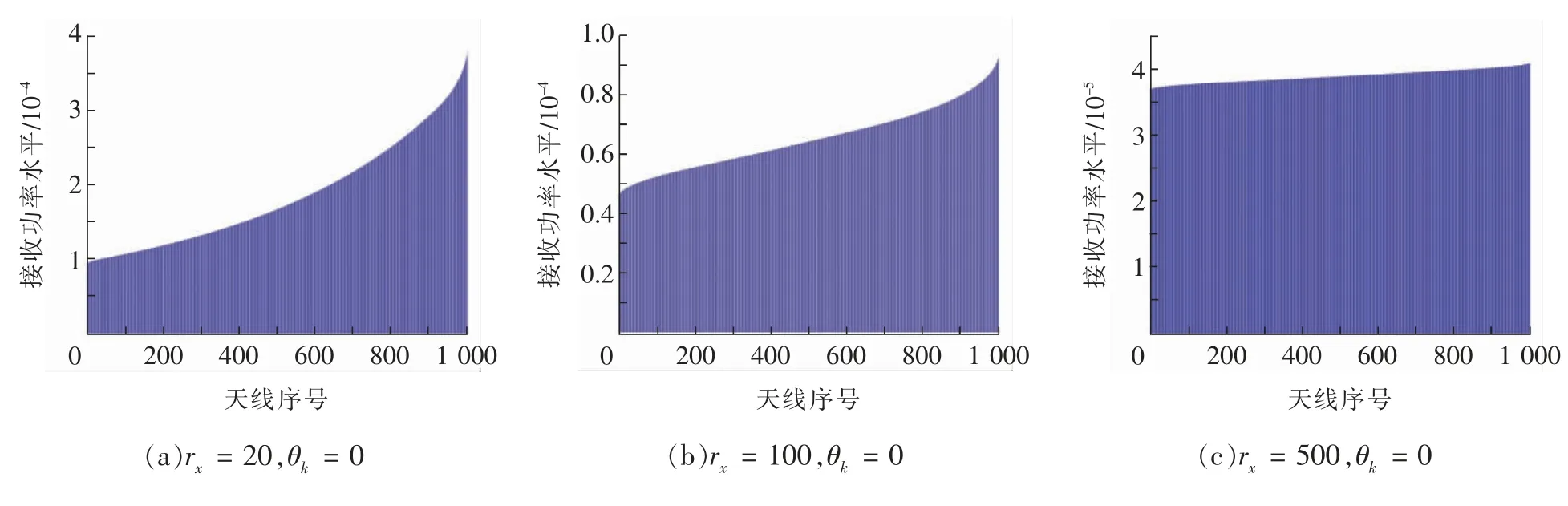
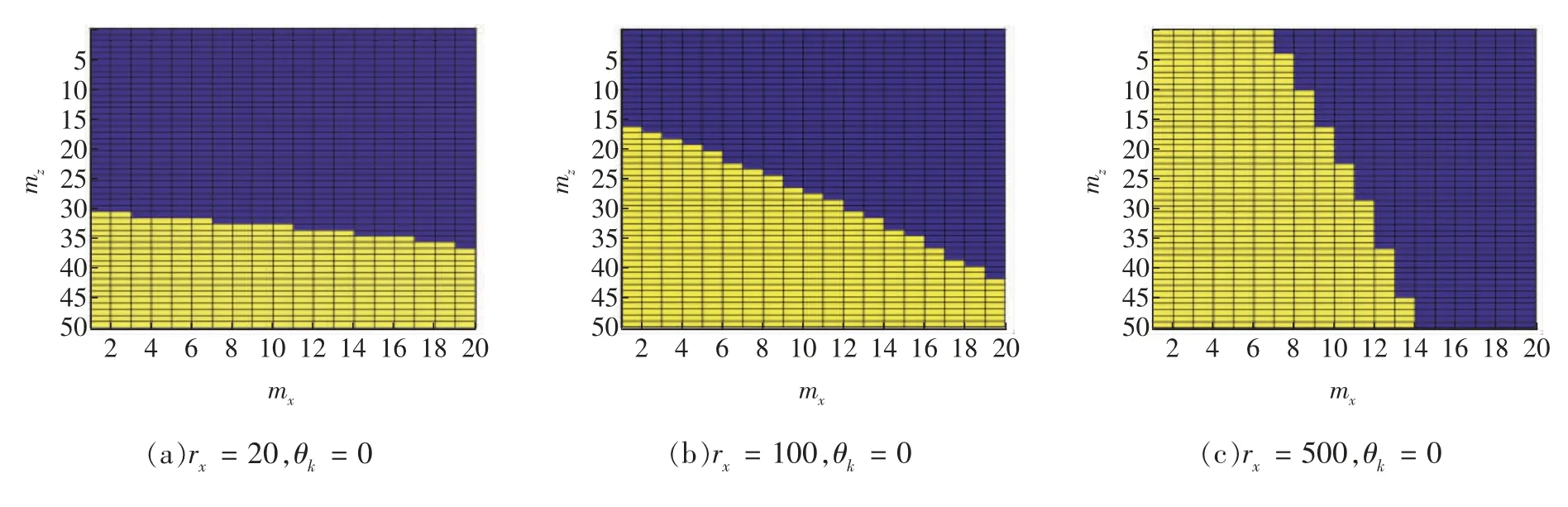
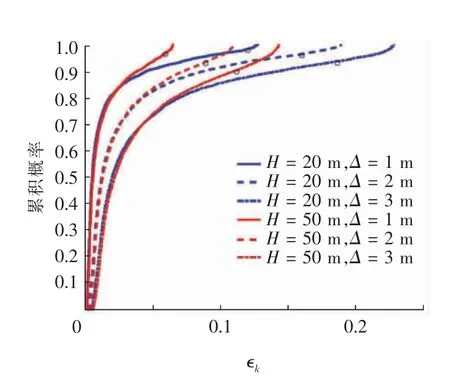
3 基于VR 的MRT 传输性能分析
3.1 两用户场景

3.2 多用户场景


4 结论与展望

