外热流扰动下航天器精密控温系统的设计及参数优化

耿利寅 张传强 童叶龙 韩东阳 孟恒辉 彭方汉

(北京空间飞行器总体设计部 航天器热控全国重点实验室,北京 100094)

近年来,随着空间高分辨率遥感载荷性能的不断提升,高精度、高稳定度控温技术成为航天器热控领域的重要组成部分[1-2]。航天器热设计实践中,一方面需在航天器表面开设散热面,其吸收的周期性外热流反过来也对设备的温度造成扰动,使其产生偏离期望值的周期性波动;另一方面,工程上普遍采用的时间离散型控温系统,在面临高精度控温场景时,其自身的稳定性将影响控温精度和稳定度指标的达成[3]。因此,航天器精密控温系统的核心任务,可归结为在保持系统自身稳定的前提下,通过合理的系统热设计和控制参数的选择、优化,最大限度地抑制因外热流扰动引起的被控对象温度波动[4]。

目前航天领域高精度控温系统设计,除了必要的提高测温精度[5]以外,主要侧重于系统热控方案的设计,如设计合理的散热通道、有效的被动热控措施和控温加热功率等[6]。对于控制部分,如控温算法和参数的选择、优化等,通常较少涉及,一般仅根据经验选取或直接指定[7],再在热试验中视实际效果而适当调整。有一定的随意性,缺乏系统的、规范性的理论指导。

本文在前期对离散型控温系统内部稳定性研究[3]的基础上,根据精密控温系统的典型场景,建立了融合空间外热流扰动、系统热控状态和控制算法的统一控温系统模型。在对模型进行线性化处理后,采用频率响应法对系统进行分析,获得了系统稳态输出的理论解。本文总结并验证了各参数对输出稳定性影响的一般规律,提出了提高系统输出温度稳定性的热设计和控制参数优化原则和方向,并以海洋盐度探测卫星综合孔径辐射计天线接收机的高稳定控温设计为例进行了说明。

1 外热流扰动下航天器主动控温系统数学模型

1.1 模型建立及其线性化

考虑外热流扰动下航天器主动控温系统的典型场景,如图1所示。考察被控对象的热环境,首先其与散热面之间有导热和辐射换热关系,根据文献[3]的说明,为实现模型线性化可将换热关系简化为等效热导K;其次,散热面直接面对空间背景,一方面将热量辐射到空间,另一方面也会吸收周期性的外热流Q;同时,被控对象上施加了主动控温功率P,此为控制量,目的是将被控对象的温度稳定地控制到预期的目标温度上。

图1 外热流扰动下主动控温系统模型Fig.1 Model of active temperature control system affected by heat flux

将图1所示系统进行抽象化处理,定义被控对象为节点1,散热面为节点2。设节点1的质量为m1,其比热容为c1,温度为T1。主动控温加热的功率P,为控温设备的输出。在不同的控温算法下,P根据T1的变化过程计算得出。节点2的质量为m2,比热容为c2,温度为T2。散热面吸收的空间外热流为Q,其对空间背景的辐射面积为A,红外发射率为εh,辐射换热系数为B。上述参数中,T1、T2、Q、P为时间t的函数,其他均为常量。

图1所示主动控温系统中,节点1的能量平衡方程为

(1)

对于PI控温,加热功率的输出算法为

(2)

式中:Ph为控温加热回路的设计最大功率;Tu为比例控温的温度阈值上限,Td为下限,即当温度T在二者之间时,控温功率按比例输出。i为PI控温算法的积分系数,单位为s-1;Ts为设定的控温目标温度。当i=0时,PI控温退化为比例控温。

式(2)代入式(1),并定义新系数将复杂的常系数替代,式(1)可简化为

k1(T2-T1)

(3)

式(3)中

(4)

(5)

对于节点2,其能量平衡方程为

(6)

式(6)中,σ0为Stefan-Boltzman常数,对该式进行同样的简化,可得

(7)

式(7)中

(8)

(9)

(10)

为实现模型的线性化,将式(10)中b近似为定值。经分析,在航天器散热面通常所处的温度范围内,这种近似处理引起的误差在10%以内,不影响本文分析结果和研究结论。

这样式(3)、(7)联立组成的线性微分方程组,即为图1所示主动控温系统的数学模型。

1.2 模型的稳态输出求解

航天器主动控温系统在轨长期运行,主要是其稳态输出决定了控温的品质,故可采用频率响应法进行分析[8]。本文研究内容为控温系统在外热流扰动下输出温度的波动问题,系统输入为散热面吸收的外热流,输出为被控对象的温度。按照傅里叶变换,周期性外热流可视为一系列正弦波叠加的结果,现将系列中某一频率为ω的波动分量作为系统输入,即

Q(t)=Qvsin(ωt)

(11)

式中:Qv为外热流波动的振幅。将式(11)代入式(9),得

(12)

为分析系统的稳态输出,需求得系统的传递函数。首先对(3)、(7)两式进行拉普拉斯变换,再将所得两方程联立,整理得外热流函数q到被控对象温度T1的传递函数

(s+k2+b)-k1k2s}

(13)

对于式(3)、(7)定义的线性定常系统,当其输入为正弦波时,其稳态输出也是一个同频率的正弦波,仅幅度和相位不同。在振幅为Qv,频率为ω的正弦外热流扰动下,被控对象的温度T1的振幅为[9]

(14)

式(14)中,j为虚数单位。对于航天器主动控温系统,由于绕地球运动,其外热流的基频ω最高约为1.0×10-3,通常p的范围约为0.01～2.00,i的取值范围为0.01～1.00,即使考虑各阶倍频,ω2也远小于pi,因此,式(14)可简化为

(15)

当i=0时,PI控温退化为比例控温,代入式(14)并考虑实际工程中p、b、k1、k2等的大小关系,可得采取比例控温时的输出温度振幅

(16)

1.3 理论解的验证

因比例控温是属于PI控温的一种特殊情况,以下仿真验证仅针对PI控温进行。为验证上述理论分析结果即式(15)的正确性,建立一个与图1所示热物理模型完全一致的主动控温系统数值仿真模型。该模型的主要热物理参数取值见表1。在不同的控制参数取值工况下,分别采取本文理论推导和数值仿真的方法计算被控对象的温度振幅,结果及其对比如表2所示。

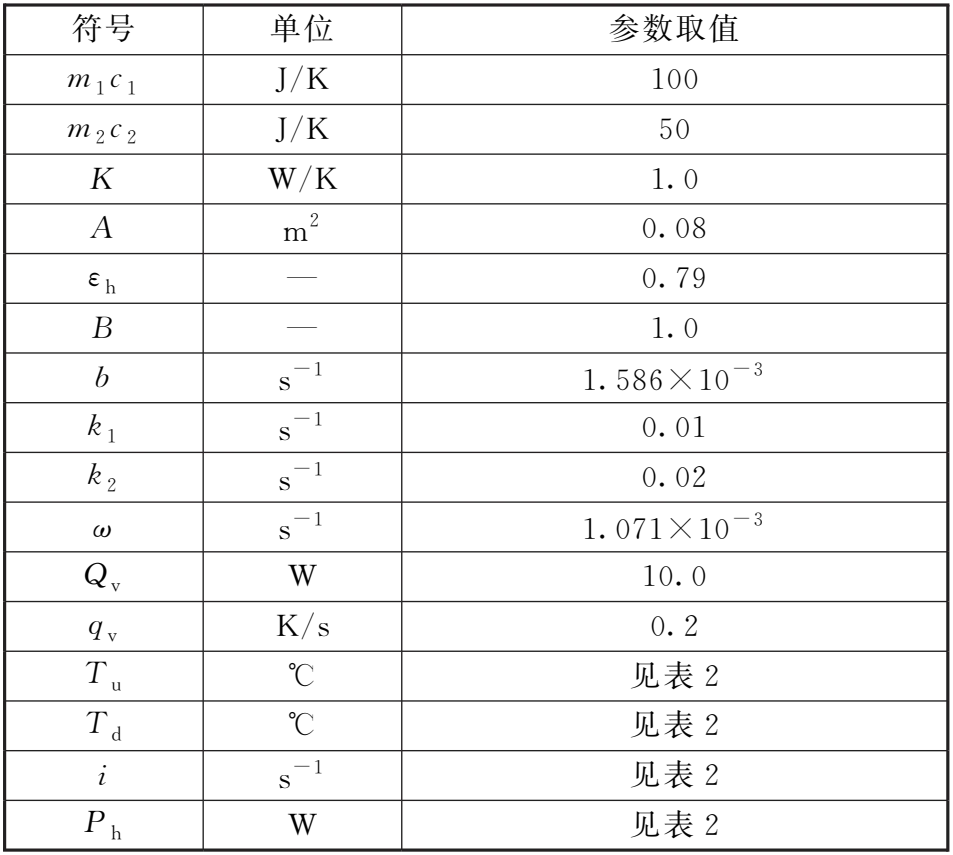
表1 验证模型的参数定义及取值Table 1 Definition and values of verifying model

表2 理论分析与仿真计算的输出温度振幅及对比Table 2 Comparing of temperature amplitude between theoretical and numerical analysis

从表2的结果对比可见,数值仿真的结果与理论分析即式(14)或(15)的结果一致,变化趋势相同,且随着pi的增加二者偏差迅速减小,尤其在控制参数的常用取值范围内,理论分析与数值仿真的结果高度一致,验证了本节理论分析的正确性。

2 理论解的分析和参数优化原则

2.1 各参数对温度稳定性的影响分析

1)积分因素对输出温度稳定性的影响

比较式(15)和(16),若令Tv-P和Tv-PI分别代表比例和PI控温算法输出的温度振幅,r为二者之比,则式(15)除以式(16)得

(17)

考虑到式(17)中分母分子括号中的部分数量级相等,且航天器热控设计实际中ω和i的大小关系,式(17)可化简为

(18)

式(18)说明,控温算法中积分项的引入,除可以将被控对象准确控制到目标温度Ts上以外[10],还可以显著减小外热流扰动引起的温度波动幅度。

2)热物理参数的影响

式(15)中主要参数不是直观的热物理参数(系除以节点1、2的热容所得),为直接分析各热物理参数的影响,将式(4)、(5)、(8)、(10)、(12)等代入式(15),得

(19)

式(19)中,将散热面向空间背景的辐射换热转化为了等效热导KR的形式,以便于比较。分析式(19),各热物理参数对输出温度振幅的影响如下。

(1)输出温度的振幅Tv,与吸收外热流振幅Qv成正比,而吸收外热流的波动通常是可见光(包含太阳直照和行星反照)造成的,因此减小散热面的太阳吸收比可直接、有效地降低温度的波动。

(2)被控对象温度振幅与节点1、2的热容无关,说明改变被控对象和散热面各自的热容,包括改变二者的比例关系,对提高温度稳定性均没有帮助。这与通常的直觉不一致,原因在于式(15)、(16)的简化中忽略了扰动项中的高频成分,实际当面临外热流突变时(含有高频成分),增加热容仍是阻止温度剧烈波动的有效措施。

(3)式(19)中KR与K的比值越大,系统输出温度振幅越小。这说明提高散热面对空间的辐射换热与被控对象与散热面之间等效热导的比值,可以提高输出温度的稳定性。

(4)外热流扰动的频率越低,被控对象温度波动振幅越小,说明PI控温算法对较低频率的外热流扰动抑制效果明显,对于高频扰动效果会变差,这与相关文献的设计和试验结果一致[11]。因此,选择散热面的朝向时应尽量避免外热流突变,降低外热流扰动中的高频成分。

3)控制参数的影响

(1)输出温度的振幅,与设计加热功率Ph成反比。因此,一定范围内(后文详细说明)增加设计加热功率可减小输出温度的波动。

(2)Tu-Td称为控温参数中的比例控温带,该值越小,越有利于抑制输出温度波动。工程实际中,只有提高测温精度,才能最大限度减小该值,这也是高精度控温系统必须首先提高测温精度的原因。

(3)积分系数i与输出温度振幅成反比,增加积分系数可减小输出温度的波动。

2.2 系统设计和控温参数优化方向

2.1节说明了各物理参数和控制参数对系统输出稳定性的影响,但实际热设计中,这些参数受到软硬件条件的限制,同时它们之间也是互相约束的,并不能随意取值。以下说明精密控温系统设计中,热物理参数和控制参数取值优化的原则、方向和思路。

(1)通常的热设计中,热耗决定散热需求,同时需综合考虑航天器构型等多方面约束选定散热面的朝向、面积等;另外,被控对象与散热面之间的综合热导K也是根据散热需求设计的。这些状态调整和优化的空间有限。但尽量选择外热流波动小,特别是剧烈突变小的方向开设散热面,尽量减少散热面的太阳吸收比αs,增加其红外发射率εh,仍然是提高温度稳定性直接、有效的优化方向。

(2)控温算法方面,降低输出温度振幅Tv的途径主要在于控制系数p、i的选定上。根据此前的研究结论[3],对于设计中普遍采用的时间离散型主动控温系统,其内部(或称自身)稳定性是参数设计的首要约束。对于本文1.1节所述的控温系统模型,保持其自身稳定的充要条件是

2pΔt+piΔt2≤4

(20)

并且式(20)中等号左侧的值越接近4,系统稳定性就越差,其受到扰动后稳定的过程就越长。由于控制周期Δt已由硬件系统确定,式(20)即为设计中p、i参数选定的约束条件。

(3)由式(15)可知,当其他热物理参数确定后,输出温度振幅Tv与控制参数p、i的积成反比,因此要减小Tv,应在保持系统稳定即满足式(20)的前提下,尽量增大pi的值。

(4)实际设计中,由p的定义式(4),加热回路的设计功率Ph由系统热设计和控温设备硬件共同决定,而比例控温带Tu-Td应不小于系统测温分辨率的5～10倍,最终也是系统硬件决定的。因此,系统控制参数优化应首先根据热设计的需求和硬件约束确定p,再在式(20)的约束下选定、优化i。总的趋势是i越大,稳态输出波动越小。可通过仿真计算验证控温的效果和指标满足情况。在满足输出温度的稳定性指标并留有充分余量的基础上,i应选取较小的值,以利于系统受到扰动后的快速稳定。

3 设计实例验证

3.1 综合孔径辐射计天线状态介绍

以海洋盐度探测(HY-4A)卫星综合孔径辐射计天线接收机的高稳定控温设计和参数优化为例,说明本文所述的热设计和参数优化的原则、方向和实施途径。

HY-4A卫星运行于高度约654.7km的太阳同步圆轨道上,周期约97.8min,降交点地方时6:00。该卫星载荷综合孔径辐射计天线由一个中心舱和3条天线支臂组成,支臂为长条形,安装在卫星载荷舱外,其辐射面朝向地面。每条支臂内安装有天线单元和接收机组成的阵列。天线长期工作,每台接收机热耗1.8W,要求接收机温度稳定性优于0.1℃,即其温度振幅Tv≤0.05℃。

本文选择2台典型接收机作为研究对象。如图2所示为天线支臂内的构型示意图,图中X方向是支臂长度方向,每条支臂X方向排列有16套相同的天线单元和接收机,此处只给出其中一段,包含2台接收机和一套天线单元。

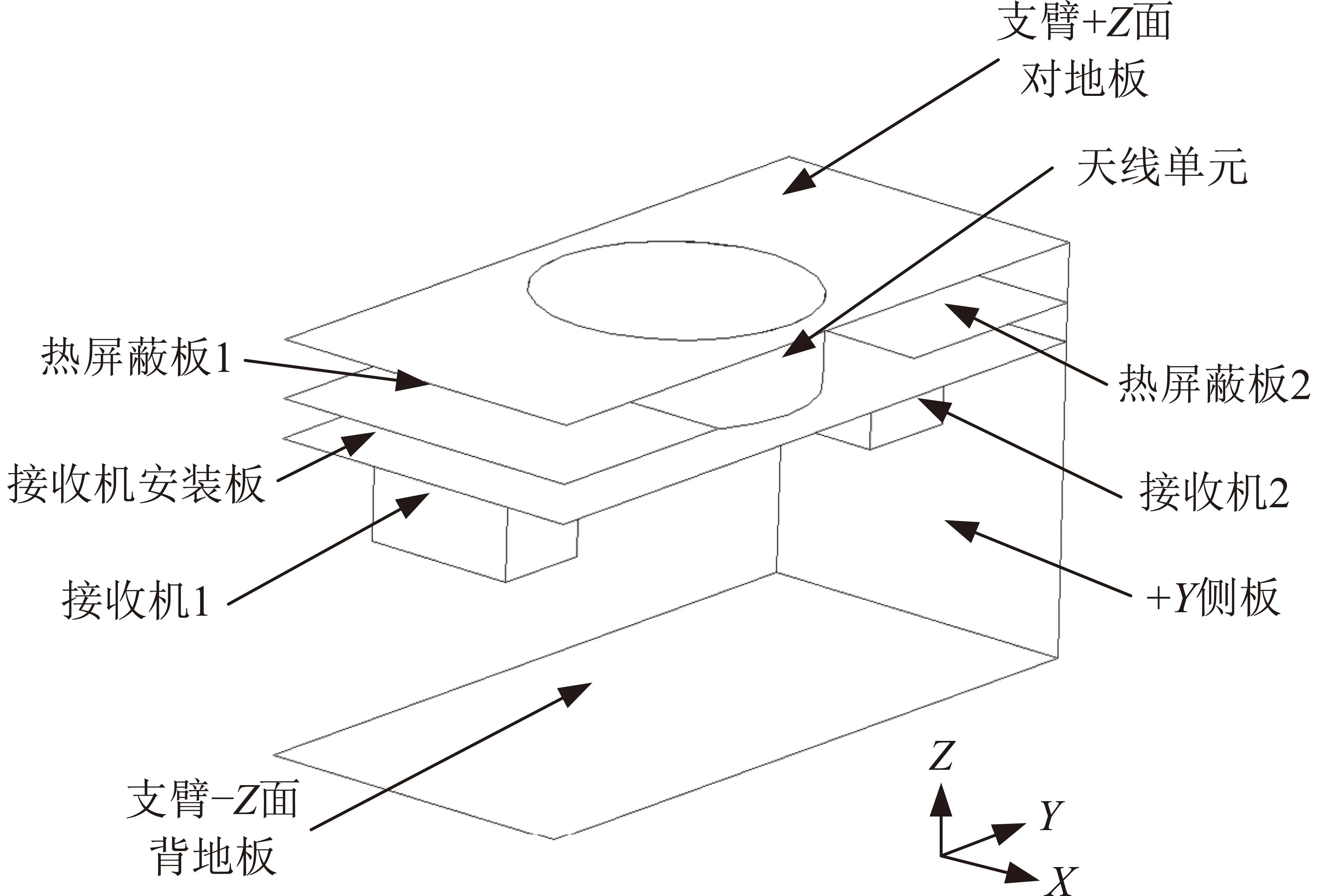
图2 天线支臂内部构型示意图Fig.2 Internal configuration diagram of antenna branched arm

根据该卫星在轨飞行姿态,图2中,+X方向为卫星飞行方向,+Z为对地方向,+Y方向为背阳面。天线支臂的±Y侧板、+Z面对地板和-Z面背地板均为碳纤维蒙皮铝蜂窝板。另外,支臂内还设置了一块平行于对地板的安装板,为接收机、天线单元等提供支撑和安装界面。

3.2 天线接收机热控设计及其优化

首先选择外热流最小且最稳定的+Y侧板作为散热面。但+Y侧板面积不足,必须在其他方向开设辅助散热面。受整星构型的限制,只能将支臂的+Z面即对地板作为辅助散热面。但晨昏轨道夏至时对地面外热流波动剧烈,如图3所示。由此对接收机的温度产生强烈扰动,这是接收机高稳定温度控制面临的难题之一。

图3 天线+Y和+Z方向到达热流密度Fig.3 Arrived heat flux in +Z and +Y direction of antenna

根据2.2节的分析结论,在热设计上提高接收机温度稳定性最直接和有效的措施是降低散热面的太阳吸收比αs,或增加其红外发射率εh。不同散热面涂层对接收机温度稳定性的影响见图4,图中白漆寿命末期αs=0.48、εh=0.87,而OSR寿命末期αs=0.23、εh=0.79,计算时其他参数完全一致。从图中接收机的温度曲线可知,OSR作为散热面涂层时接收机的温度稳定性显著优于白漆,故应选择OSR作为综合孔径辐射计天线散热面的涂层。

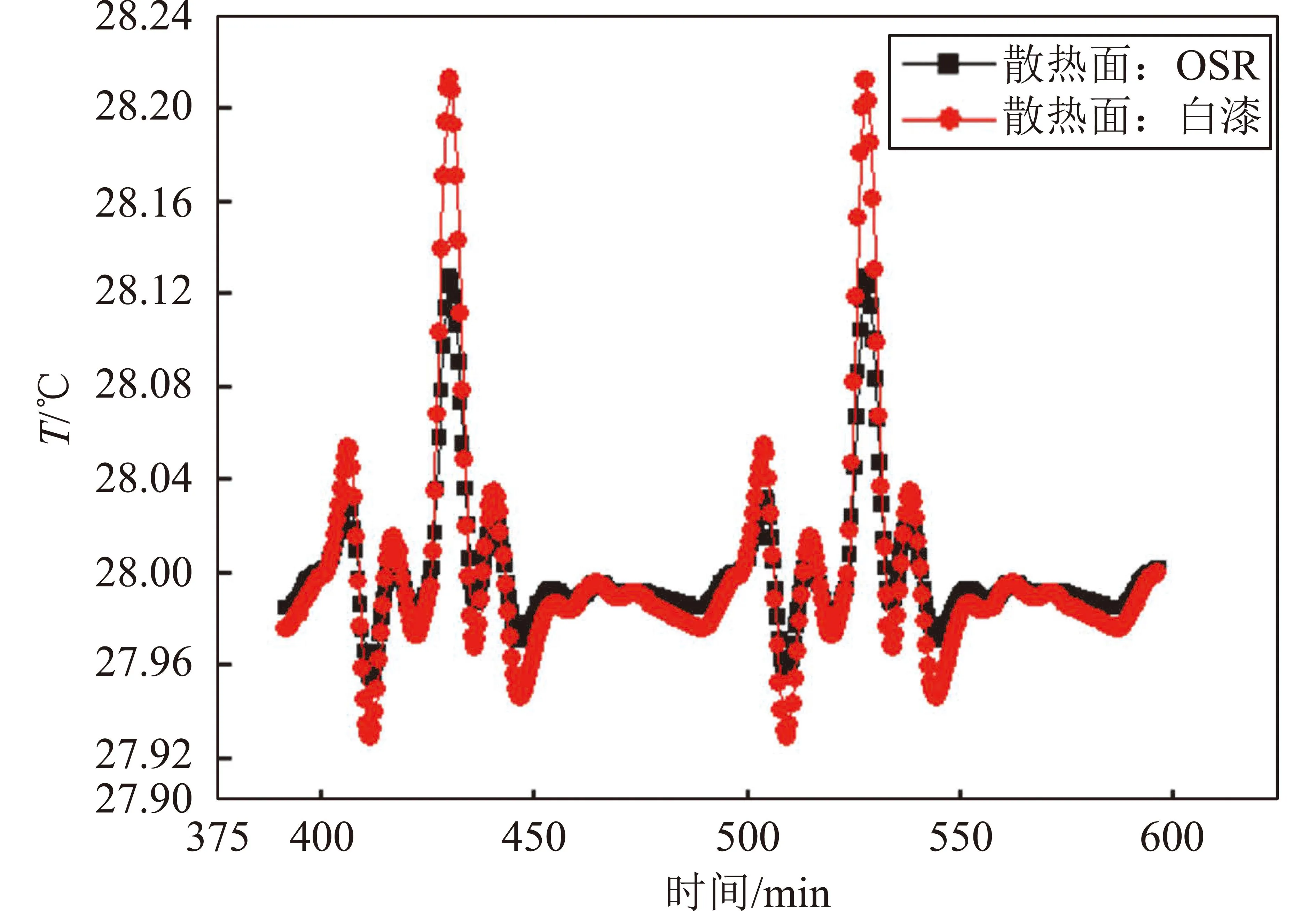
图4 不同散热面涂层对接收机温度稳定性的影响Fig.4 Influence of different coatings on temperature stability of receivers

同时,2.2节的分析说明:在满足散热需求的前提下,降低被控对象和散热面之间的等效热导也能提高温度稳定性。因此,在接收机安装板和+Z散热板之间安装一层双面发黑的铝合金热屏蔽板。热屏蔽板对接收机温度稳定性的影响结果见图5,图中两种结果的其他参数完全一致。从图中温度曲线可知,增加热屏蔽板后,接收机的温度波动幅度从0.21℃降为0.17℃。

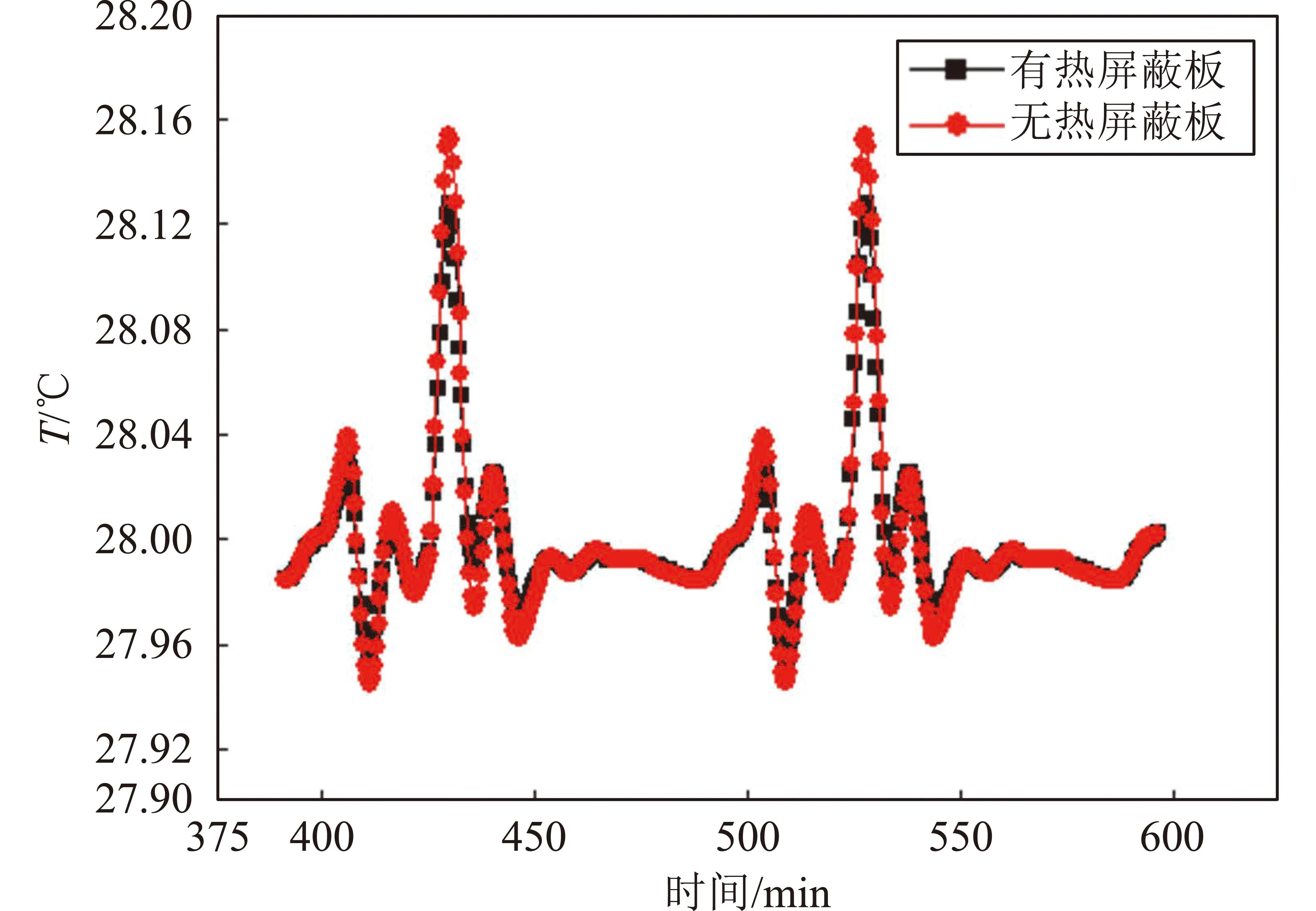
图5 热屏蔽板对接收机温度稳定性的影响Fig.5 Influence of thermal shield on temperature stability of receivers

3.3 接收机控温参数的设计和优化

每台接收机质量m1为0.32kg,热容m1c1约300J/K。在每台接收机上布置Ph=4W的加热器,控制周期Δt为5s,测温精度为0.01～0.02℃,故比例控温带Tu-Td最小为0.2℃。按照式(4)根据不同的Tu-Td可计算系统比例系数p。按照式(20)的约束,可得积分系数i应不超过0.79。在此范围内,针对不同的p、i参数取值,采用数值仿真模型计算接收机在轨温度。计算的具体工况为夏至、寿命末期,结果见图6。图中所示为典型p、i取值时的接收机温度曲线。图中曲线为达到平衡后约2个周期的温度结果,忽略了从初始温度达到平衡的中间过程。

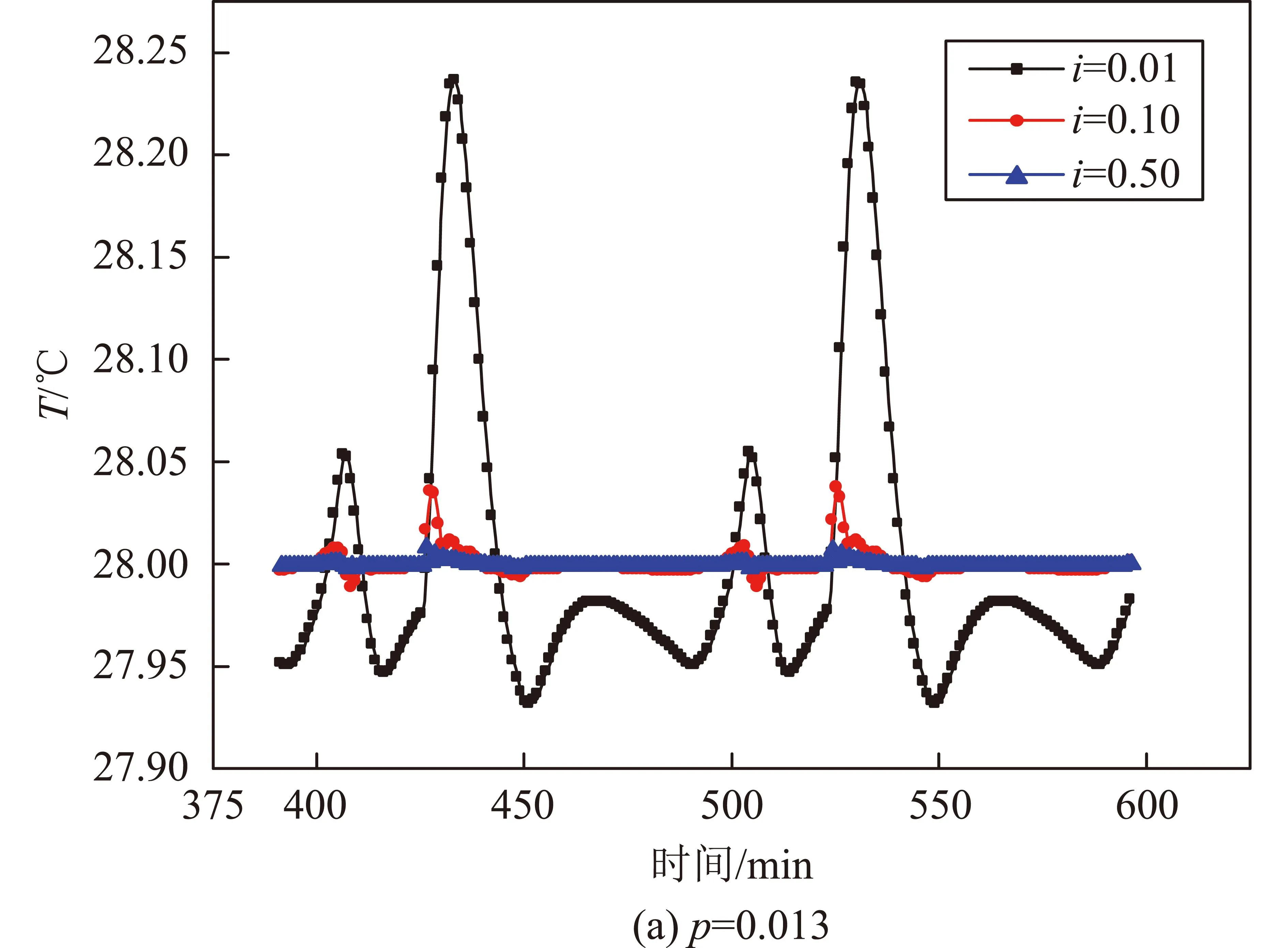
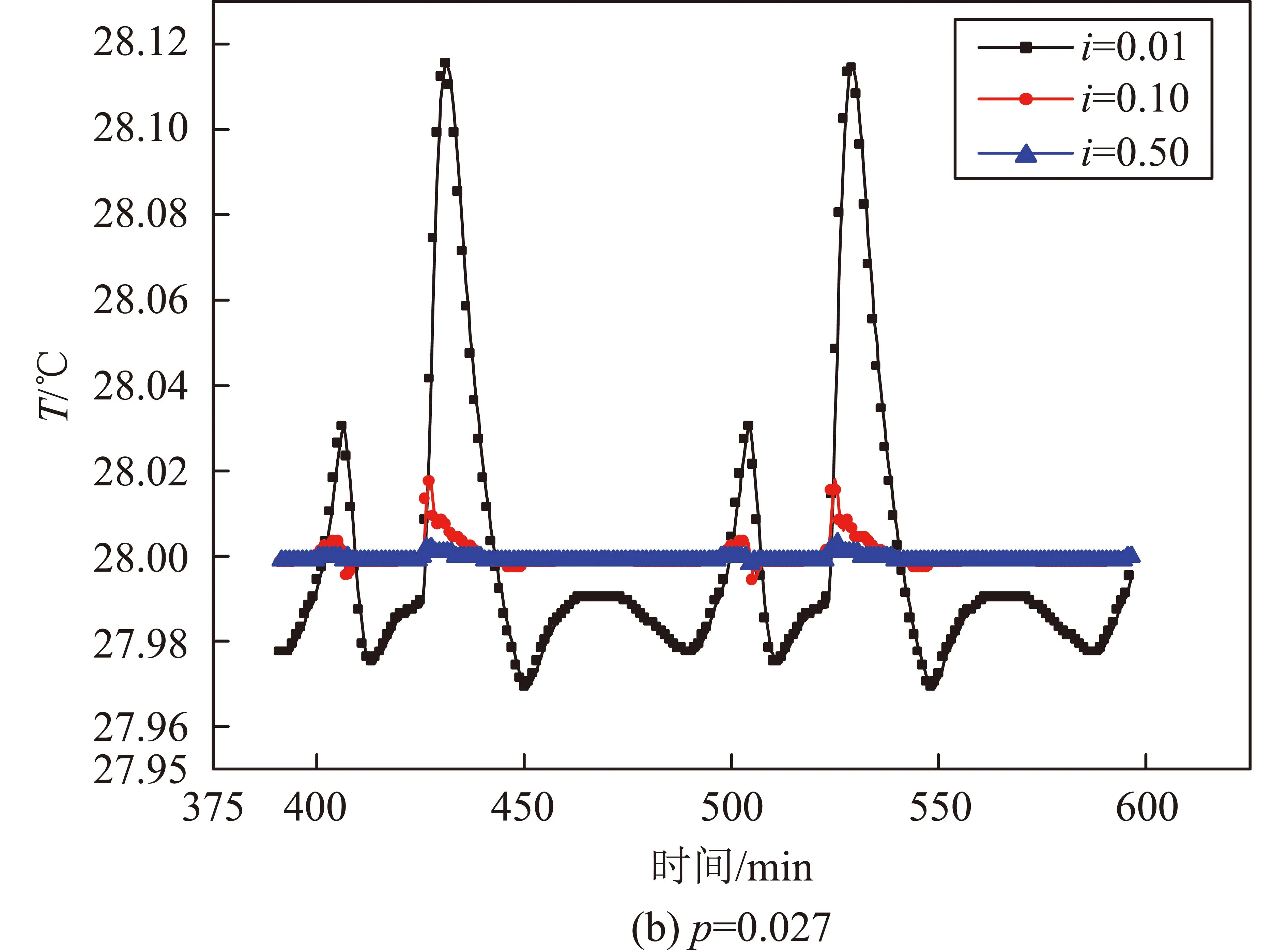
图6 不同p、i参数取值时接收机的温度曲线Fig.6 Temperature curves of receiver in different parameter p and i

图6中结果可以看出,满足系统自身稳定的前提下,当p确定时,i取值越大,输出温度的振幅越小,结果越稳定。当采取PI控温算法时,输出温度结果的振幅Tv与pi成反比。这与式(15)的结论符合,证明了本文理论分析及由此提出的优化原则的正确性和有效性。

综上,本设计实例中最终选定了Tu-Td=0.2℃即p=0.067,i=0.20作为接收机的控温参数。仿真分析表明,上述参数设置和优化获得了理想的控温效果。

4 结束语

本文通过理论分析和仿真计算,主要对航天器精密控温系统在外热流扰动下输出的稳定性进行研究,有以下主要内容和结论:

(1)根据航天器主动控温系统的典型应用场景,建立了融合系统热控状态和控温算法,包含热物理参数、控制参数和外热流输入等因素的统一数学模型。结合航天器热设计的工程实际,通过简化实现了模型的线性化,为进一步理论分析提供基础。

(2)应用基本控制理论对系统进行分析,采用频率响应法获得了典型外热流输入下主动控温系统稳态输出的理论解,通过合理简化获得了各热物理参数、控制参数与输出温度波动幅度之间的定量关系,主要结果见式(15)、(19)等,本文进一步讨论了各参数对系统输出温度稳定性的影响。

(3)在以上理论分析和讨论的基础上,结合此前得出的离散控温系统自身稳定条件和热控系统各参数的约束关系,提出了以降低外热流扰动引起的温度波动为目标的热设计和控制参数优化原则和方向。

(4)以海洋盐度探测卫星综合孔径辐射计天线接收机的高稳定性控温设计为实例,说明了本文提出的热设计和控制参数选取、优化的原则、思路和方向以及实施过程。通过数值仿真对不同参数取值下输出温度的稳定性进行了分析对比,验证了本文理论界的正确性和优化方法的有效性。