应用过程神经网络的航天器瞬态温度预测方法
陈冠宇 杨森 彭威 多乐乐 张健鹏 刘宪闯
(湖北航天技术研究院总体设计所,武汉 430040)
航天器在轨空间热环境复杂多变,在轨运行时各仪器设备温度受环境影响较大,同时其研制阶段的热分析、热平衡与热真空试验往往也需要耗费大量的人力、物力及时间成本,如何通过有效的温度预测提供在轨温度预警信息、提高仿真效率、减少试验成本,已受到广泛关注[1-3]。航天器热试验与在轨运行过程中,其温度变化过程伴随着时间积累效应[4],而传统的温度预测理论往往在选择初始模型的阶段就带来了一定误差,同时也难以反映热传递中的时间累积效应,因而能够预测的时间段较短且精度欠佳。
随着神经网络模型的广泛应用,对于大多数问题而言,其变化往往与时间累积效应有着密切的关系,例如温度变化过程、化学反应过程及股市的波动等,而传统的人工神经网络的几何点式的瞬时输入只在理论上存在。过程神经网络是对一般人工神经网络的一种推广,其输入与连接权均为时变函数,且连续性、逼近性及计算能力均得到了证明[5-6],拓宽了原模型的适用范围,是一种更加广义化的模型。航天器各部件间传热所引起的温升与温降是一个伴随着时间累积效应的过程,过程神经网络能够较好地反映过程量,进而体现传热过程中的时间累积效应[7]。本文提出应用过程神经网络的航天器瞬态温度预测方法,以航天器在轨温度实测数据为基础,结合相空间重构理论完成样本集的构建,基于过程神经网络建立瞬态温度预测模型。该方法能在满足工程精度要求下对航天器瞬态温度进行快速预测,可实现航天器复杂空间热环境下的在轨温度预警。
1 航天器瞬态温度预测方法
1.1 温度预测方法原理及流程
基于本文所研究的航天器瞬态温度预测具体问题,对温度预测原理及流程进行相应说明。本文将温度预测的流程分为3个部分,分别为学习过程、测试过程及预测过程,预测原理及过程如图1所示。

图1 温度预测原理及过程示意Fig.1 Principle and process diagram of temperature prediction
图1中,T0为样本集中训练集起始点航天器测点温度,τ1与T1分别为样本集中测试集起始点的时间与航天器测点温度,τ2与T2分别为样本集中测试集终止点的时间与航天器测点温度,τE与TE分别为预测过程终止点的时间与航天器测点温度。
本文首先将学习过程与测试过程中的样本集分成训练集与测试集,应用相空间重构理论对样本集进行重构,建立过程神经网络模型,提取[0,τ1)时间段内的航天器温度数据作为训练集,将其用于模型训练,并应用学习算法完成航天器温度信息学习;提取[τ1,τ2]时间段内的航天器温度数据作为测试集,用于模型精确度的测试;最后将[τ1,τ2]时间段内的航天器温度数据作为新增样本进行训练,最终得到训练完毕的模型,基于此模型来完成对(τ2,τE]时间段内航天器瞬态温度的预测。
1.2 应用相空间重构理论的样本集构建
在构建样本集时往往需要一定量的航天器温度数据,本文通过采用3次样条函数来完成数据间的插值与离散,即利用3次样条函数对一定数量原始数据进行插值,再以一定的密度对插值函数进行离散化处理,进而获得足够多数量的数据。
(1)

当d太小时,航天器温度相邻量的大小近乎相同,进而无法得到独立的信息;当d太大时,航天器温度相邻量的数值又会出现完全独立的情况,毫无相关性可言。因而,为了保证航天器温度相邻量的数值能在独立性与相关性之间达到平衡,需要选取合适的延迟时间。另外,为了确保航天器温度原状态空间的结构能得到完整的描述,需要满足嵌入定理[8],以此为基础结合相应算法可求出最小嵌入维数。
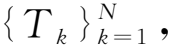
(2)
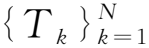
在计算CR时,延迟时间d的初值取为0,并以1为步长进行递增,直至最大值N-1。分别计算出每一步的CR值,并确定其第1个拐点所对应的延迟时间的值,则该值即为所求的d值,进而完成延迟时间的选取。

(3)
式中:|·|为向量间的欧氏距离;r>0,它被限定在各向量间最小欧氏距离与最大欧氏距离之间,本文采取等距离取值的方法;赫维赛德(Heaviside)函数δ(x)为0(x≤0)或1(x>0)。
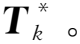
1.3 过程神经网络模型的建立
过程神经元的特点在于其能够较好地反映过程量,而航天器部组件传热所引起的温升与温降是一个伴随着时间累积效应的过程,因此理论上该模型对于传热问题较为适用。过程神经元的结构可分为4个部分,具体如图2所示。

(4)
[0,τ0]为温度函数项的积分区间,体现了航天器传热过程的时间累积效应。若温度数据间的时间差为Δτ,结合d值与m值,可得到τ0=(m-1)Δτd。

图2 过程神经元结构示意Fig.2 Process neuron structure diagram
本文选用罗吉斯蒂克函数(Sigmoid函数,也称Logistic函数)的衍生公式f(x)=1/[1+e(-x/a+b)]作为激励函数,在后续的训练过程中,可根据航天器温度变化实际趋势调整系数a与b的值,避免激励函数进入0值区或1值区。
将过程神经元与传统人工神经元结合,建立一种3层前馈过程神经网络温度预测模型。该模型除了包含输入层、输出层外,还在两者中间加入了隐层,其拓扑结构可表示为1-n-1。模型的连续性、逼近性及计算能力已得到证明,具体拓扑结构如图3所示。

图3 1-n-1模型的拓扑结构示意Fig.3 Topological structure diagram of 1-n-1 model
基于图3中的模型,可在式(4)的基础上得到
(5)
式中:νi与ωi(τ)类似,也为连接权,但不同的是,νi在这里并不是随时间变化的函数,而是作为常数,通过将隐层过程神经元输出值加权求和并减去相应阈值后,可得到输出温度值。
对于所建立的模型,在理论上已证明其具有任意精度的逼近能力,能够实现航天器瞬态温度函数的无限逼近,但需要保证隐层过程神经元具有一定数量(模型拓扑结构中的n值),如果直接设置较多的个数会使得训练时间增加、效率变低,因此选择合适数量的隐层过程神经元非常重要。目前尚无有效理论依据确定合适的隐层过程神经元数量,主要根据经验公式确定。
1.4 过程神经网络模型的学习算法
过程神经网络模型必须结合相应的学习算法才能发挥其预测能力,建立合适的学习算法,才能训练得到有效的航天器瞬态温度预测模型。本文采用正交函数系简化学习过程中的积分运算,假设温度输入函数项x(τ)与连接权ωi(τ)均为L2[0,τ0]空间上的函数,根据魏尔斯特拉斯(Weierstrass)逼近定理,若X(τ)为L2[0,τ0]空间上的函数,则对于∀ε>0,∃P(τ),使|P(τ)-X(τ)|<ε,且P(τ)为多项式。因此,x(τ)与ωi(τ)在L2[0,τ0]空间上均可由多项式函数P(τ)以任意精度逼近。在L2空间中,勒让德多项式、切比雪夫多项式及厄密特多项式等常被用于函数的正交展开。本文基于样本集开展试算与验证,选取合适的正交函数集,最终采用勒让德多项式函数系对函数进行正交展开并简化积分运算,在[-1,1]区间上,此函数系中的初始项P0(τ)与其余项Pn(τ)在一般情况下可表示为
(6)
对于本文所研究的问题,温度函数项积分区间在[0,τ0]内;同时,为了方便数值计算,将一般形式进行变换后可得到用于展开函数f(τ)的标准形式正交函数系,如式(7)~(9)所示。
(7)
(8)
(9)
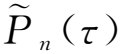
(10)
式中:ωik与ak分别为连接权ωi(τ)与温度输入函数项x(τ)正交展开后的系数;K取值为5。

(11)
在模型参数更新迭代中,为了解决传统误差反向传播(BP)算法所存在的缺陷,在原来的参数更新规则中加入了动量项与自适应调节学习率,能减小训练过程中的不稳定波动,保证稳定性,也能提高模型的学习率,进而可得到模型中的训练参数更新规则为
(12)
式中:学习过程中的迭代次数Q=1,2,…;初值Δωik(0)=Δνi(0)=Δθi(0)=Δθ(0)=0;η1(Q),η2(Q),η3(Q),η4(Q)分别对应于各参数的第Q次迭代的学习率;α1,α2,α3,α4为动量系数,一般取为0.9。

(13)
由上述训练参数更新规则可知:在训练的迭代过程中,共有(K+3)n+1个参数会不断更新,这些参数的初值均以随机数的形式给出;在迭代的过程中,会根据实际情况定义学习过程中的误差ε1>0,当迭代过程中E<ε1时,则可以停止学习;还需要采用测试集对泛化能力进行检测,满足精度要求后,将测试集作为新增样本进行学习,即可得到训练完毕的预测模型。
2 温度预测与结果分析


图4 测点1温度预测结果对比Fig.4 Comparison of temperature prediction results at measurement point 1
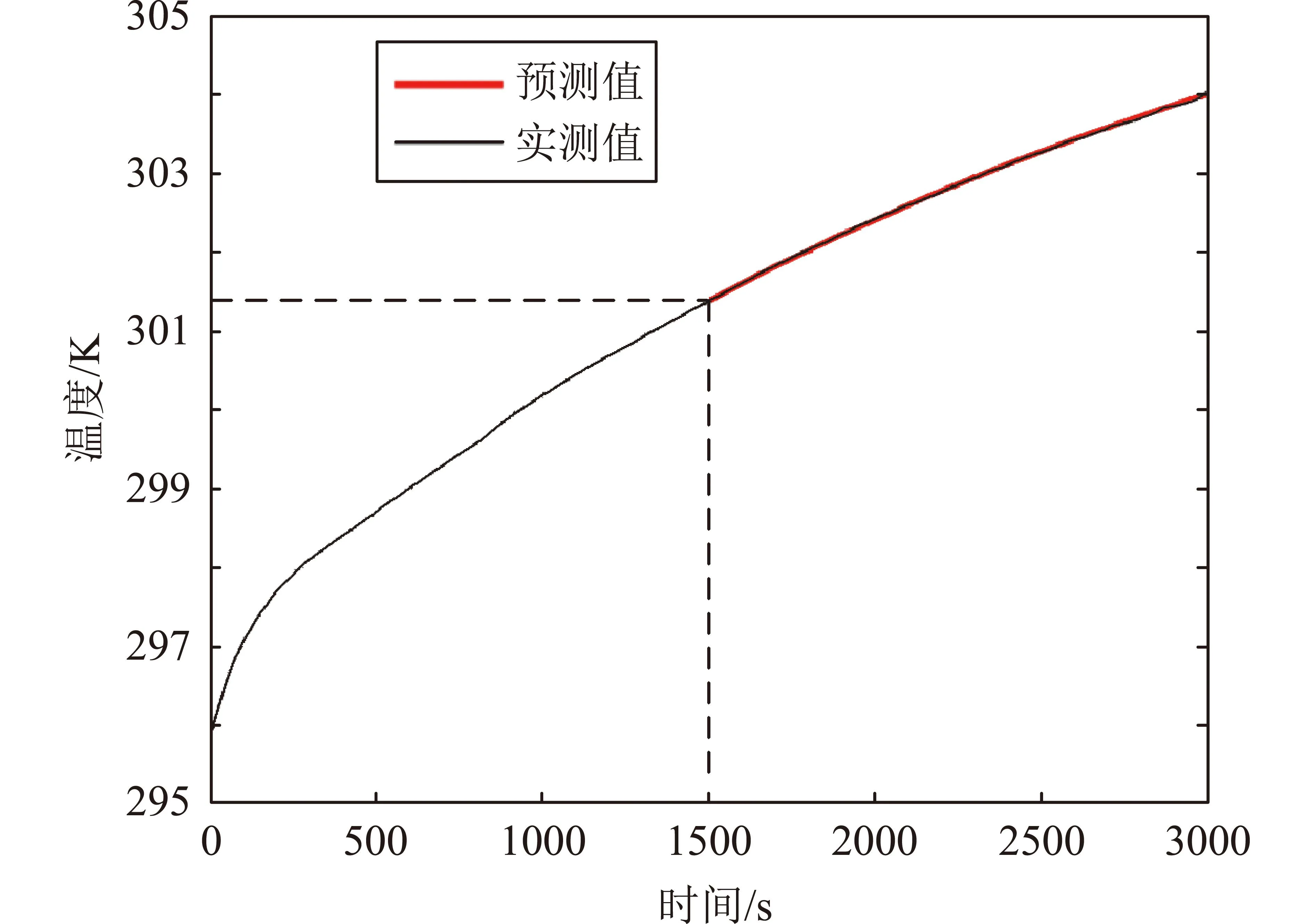
图5 测点2温度预测结果对比Fig.5 Comparison of temperature prediction results at measurement point 2

图6 测点1温度预测绝对误差Fig.6 Absolute error of temperature prediction at measuring point 1
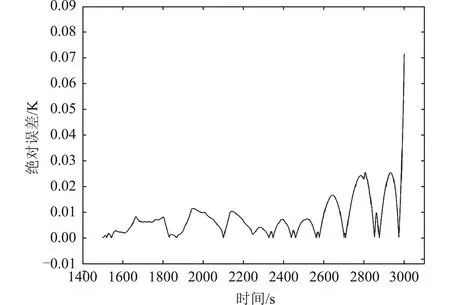
图7 测点2温度预测绝对误差Fig.7 Absolute error of temperature prediction at measuring point 2

表1 2个测点瞬态温度预测误差与耗时Table 1 Prediction error and time consumption of transient temperature at two measurement points
从表1中数据可知:测点1与测点2预测值的绝对误差最大值分别不超过0.746K和0.071K,训练时间与预测时间之和均不超过150s。由图6与图7可知:2个测点的绝对误差的变化趋势有所区别,但整体来看误差值均较小。因此,本文所建立的模型能够较好地完成航天器在轨瞬态温度预测,将预测方法应用于航天器在轨温度预警、研制阶段的热分析及热试验等任务场景中,能够有效缩短航天器研制周期,减少航天器研制成本,以及提升航天器在轨稳定运行保障水平。
3 结束语
本文提出航天器瞬态温度预测方法,应用过程神经网络建立瞬态温度预测模型,采用相空间重构理论将航天器在轨典型温度测点数据构建为样本集,并确定对应的延迟时间与嵌入维数,结合所建立的模型与算法完成瞬态温度的外推预测。通过与实测值对比显示,本文所建立的温度预测模型能够较好地满足工程应用精度要求,可实现对航天器瞬态温度的快速预测。此外,本文方法具有较强的通用性与拓展性,能够在各类具有时间累积效应的场景中推广应用。

