引力波探测中的超低频热噪声传递特性分析

亢佳贺 陈华 赵锐 杨昌鹏 赵欣 宋云飞 程文龙

(1 中国科学技术大学 热科学和能源工程系,合肥 230027) (2 合肥工业大学 汽车与交通工程学院,合肥 230009) (3 北京空间飞行器总体设计部 航天器热控全国重点实验室,北京 100094)

引力波是物质和能量剧烈运动和变化所产生的一种物质波,通过观测引力波可以了解到恒星碰撞、黑洞合并、中子星脉冲等极端天体物理事件,从而深入研究宇宙中的各种奇特现象,探测引力波的实验始于20世纪60年代的韦伯和他的共振质谱探测器[1],直接探测引力波的实验首先从地面探测开始,包括激光干涉引力波天文台(LIGO)和室女座干涉引力波天文台(VIRGO)等[2-3],但是由于地震噪声等原因,地面引力波探测器在频率低于100Hz时,探测灵敏度受到极大的限制[2,4],宇宙中信号较强的引力波源通常都分布在0.1mHz到0.1Hz的低频段,空间引力波探测可以架构臂长更长的激光干涉仪,并且具有比地面探测更丰富的波源和更远的探测距离,因此激光干涉仪空间天线(LISA),“太极”计划,“天琴”计划等空间引力波探测计划引起广泛重视[5-11]。

在星载引力波探测中,通过惯性传感器中测试质量的距离变化来探测引力波,测试质量周围的温度波动主要由太阳辐射的空间热流通量波动引起,其温度效应包括辐射计效应、辐射压效应和惯性传感器热应变波动。这些温度效应导致测试质量上的非引力加速度噪声[12-13],即温度噪声,降低了探测精度,甚至淹没了引力波信号。空间引力波探测过程只关注一定频率范围内的信号强度,敏感频段内多种温度效应导致的噪声会使测量结果产生误差,因此需要对温度噪声进行抑制。基于频域特性的温度噪声可用温度振幅谱密度(TASD)来表示。为了保证惯性传感器的灵敏度,相关研究分析认为“天琴”卫星目标频段TASD必须限制在μK/Hz1/2量级[14]。美国的LISA探路者(LISA Pathfinder)与“天琴”探测的引力波频段相同,但其在超低频段未能达到μK/Hz1/2的温度噪声抑制精度[15]。因此,超低频段的温度噪声抑制仍是一个挑战。

温度噪声抑制依赖于高精度的热控制,高精度热控的主要目的是抑制由于温度变化所导致的形变对仪器性能的影响,在激光领域、航空航天领域等领域,高精度热控不可或缺,但传统高精度热控只是针对时域温度波动的范围进行控制,如:重力场与稳态洋流探测器(GOCE)卫星要求同一轴线两重力梯度仪敏感头温度梯度不超过0.5℃[16]。由于资源的限制,空间热控以被动热控为主,以主动热控为辅,被动热控主要采用隔热材料和相变材料,相关研究主要集中在降低隔热材料的导热系数[17-18]和提高相变材料的潜热[19-20]。主动热控制主要采用比例、积分、微分控制(PID)方法,相关研究通过算法优化PID实现高精度温度稳定,在光学透镜、激光敏感器件等电子产品领域较为先进[21-23]。然而,主动热控制需要复杂的控制和测量系统,以及实现有效温度控制的算法,增加了系统复杂性和计算时间。

目前星载引力波探测器主要采用被动式热控制进行时域温度控制,包括隔热材料和加热器补偿[15,24]。加热器补偿基于温度检测被动调节加热功率,主要关注温度在时域上的波动,存在时滞。通过对PID主动控制结果进行分析,即使时域温度稳定性达到1mK,频域温度噪声仍大于10mK/Hz1/2[25]。文献[26]针对“天琴”引力波探测器提出分层分级、控制算法与材料结构结合的总体热控方案设想。主动与被动热控的有机结合需要探究频域温度特性,目前对温度噪声的研究还很有限,特别是在超低频下温度噪声的传输规律及其抑制机制尚不清楚。

针对上述问题,本文基于温度噪声频域特性,研究不同因素对温度噪声传递的影响。基于引力波探测敏感频段,探究被动热控材料对不同频率温度噪声的抑制效果,根据得到的频域特性提出温度噪声针对性控制方法。

1 分析方法及其验证

1.1 分析模型

为了说明被动式热控材料的热物性和热源的光谱特性对温度噪声的影响,建立温度噪声传输模型,模拟材料为长方体被动热控材料,设几何尺寸的长度(z轴)为Z,宽度(y轴)为Y,厚度(x轴)为L,热流方向垂直于z-y面,采用正弦波形式的输入热流(图1)。本文基于有限体积法,假设模拟材料处于真空和无重力环境中,波动热流从一侧输入,经过被动热控材料,以辐射换热的方式散热。

图1 物理模型Fig.1 Physical model

1.2 数学模型

建立温度在时域的波动模型,温度场控制方程为

(1)

式中:T为温度(K);ρs为测试材料的密度(kg/m3);cp为测试材料的比定压热容(J/(kg·K);κ为测试材料的导热系数(W/(m·K)。

边界条件为x=0的平面为输入具有频谱特征的热通量

-κ·∇T=Q(t)

(2)

式中:Q(t)为(叠加)正弦波形式的热流(W/m2),其余边界面为辐射换热

(3)

式中:As为s表面的面积(m2);σs为Stefan-Boltzmann常数,ε为模拟材料发射率;Ti是模拟材料表面的温度;Tb是环境温度。初始条件给出

T=T0,x≥0,t=0

(4)

式中:T0为初始温度(K)。

离散数据的功率谱密度可得到[27]

(5)

式中:GD(ω)为温度时间数据T(t)的功率谱密度(K2/Hz);N为时间记录中的数据点总数;T(t)为温度时间信号在第t个时间瞬间的值,其中t=0,…,N-1;j为虚数单位。

温度振幅谱密度满足

TTASD=GD(ω)1/2

(6)

1.3 网格独立性验证

为降低网格数量对仿真结果的影响,针对仿真模型进行网格独立性验证,不考虑重力作用,采用空间辐射模型,测试材料为复合聚氨酯材料,采用傅里叶红外光谱仪测得辐射发射率为0.79,经过Hot Disk热常数分析仪测试,热导率为0.04W/(m·K),比热容为885.35J/(kg·K),密度为100kg/m3,Z=0.1m,Y=0.1m,L=0.01m,采用瞬态计算,网格数量分别为326960、489577、741420、854441、1012631,评判指标为观测点的温度噪声值,结果如图2所示,综合考虑,本文后续模拟仿真选用的网格数为741420。

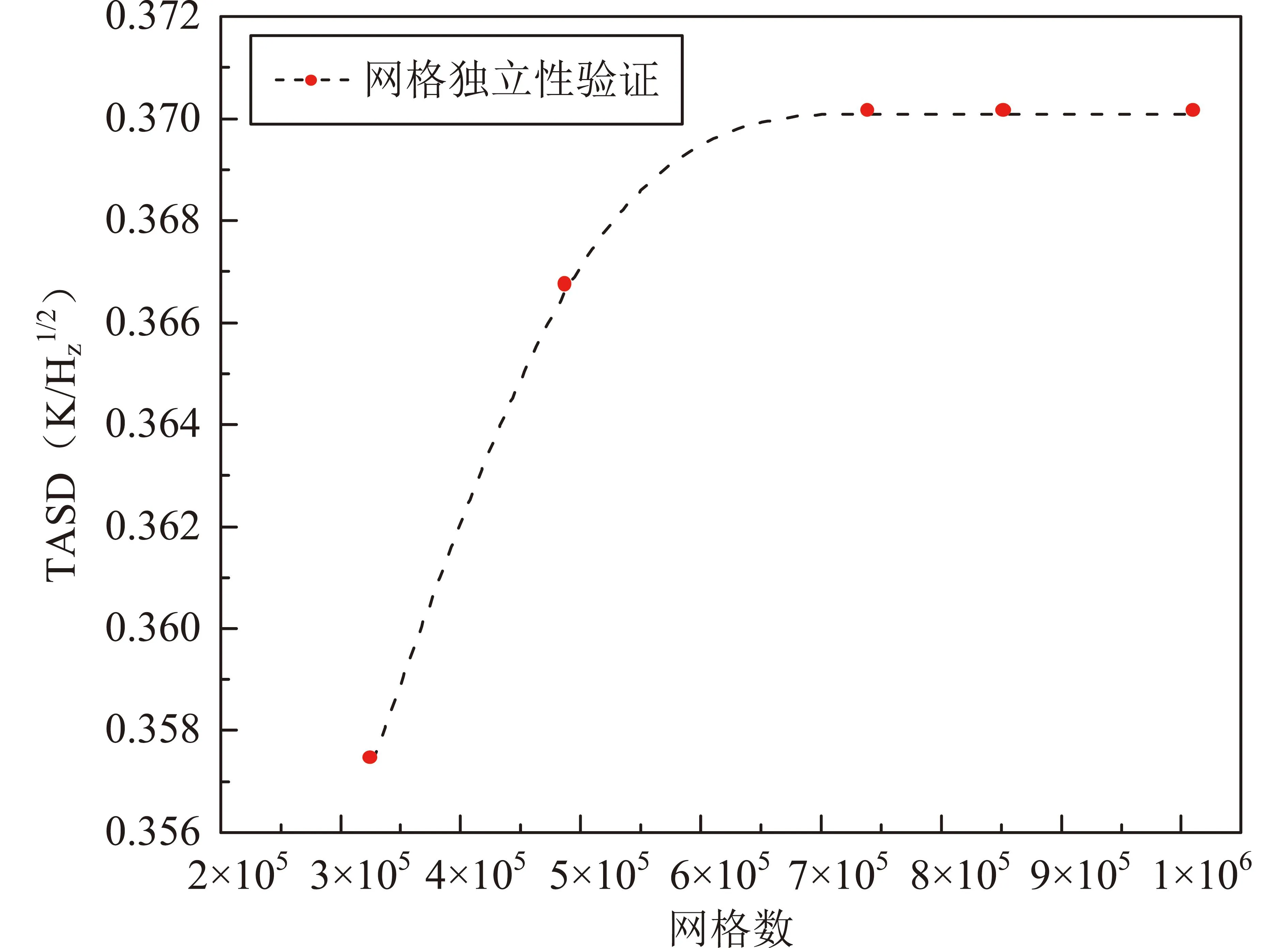
图2 网格独立性验证Fig.2 Grid independence verification

1.4 试验验证

测试材料尺寸结构为Z=0.1m,Y=0.1m,L=0.01m,测试材料为复合聚氨酯材料,辐射发射率为0.79,热导率为0.04W/(m·K),比热容为885.35J/(kg·K),密度为100kg/m3,采用PT100四线制热电阻温度传感器测温,通过信号发生器产生正弦波信号,信号发生器将信号传递给环形变压器和功率放大器,功率放大器将放大后的信号传递给聚酰亚胺加热膜,通过以上方法产生波动热流,测试材料置于真空箱中,真空度为100Pa,通过航空插排实现真空箱内外电路连通,真空箱置于恒温试验箱中,试验时保持环境温度25℃。

试验测量中的不确定度按照文献[28]给出的方法确定。每次试验测量重复数次测量参数的最大不确定度见表1。不同频率下的时域和频域验证结对比如图3所示。输入热流频率分别为10、15、20mHz,每次试验的振幅保持在5Vpp,每秒记录温度数据,仿真输入热流通过试验热通量传感器获得。

表1 参数的不确定度Table 1 Uncertainty of parameters

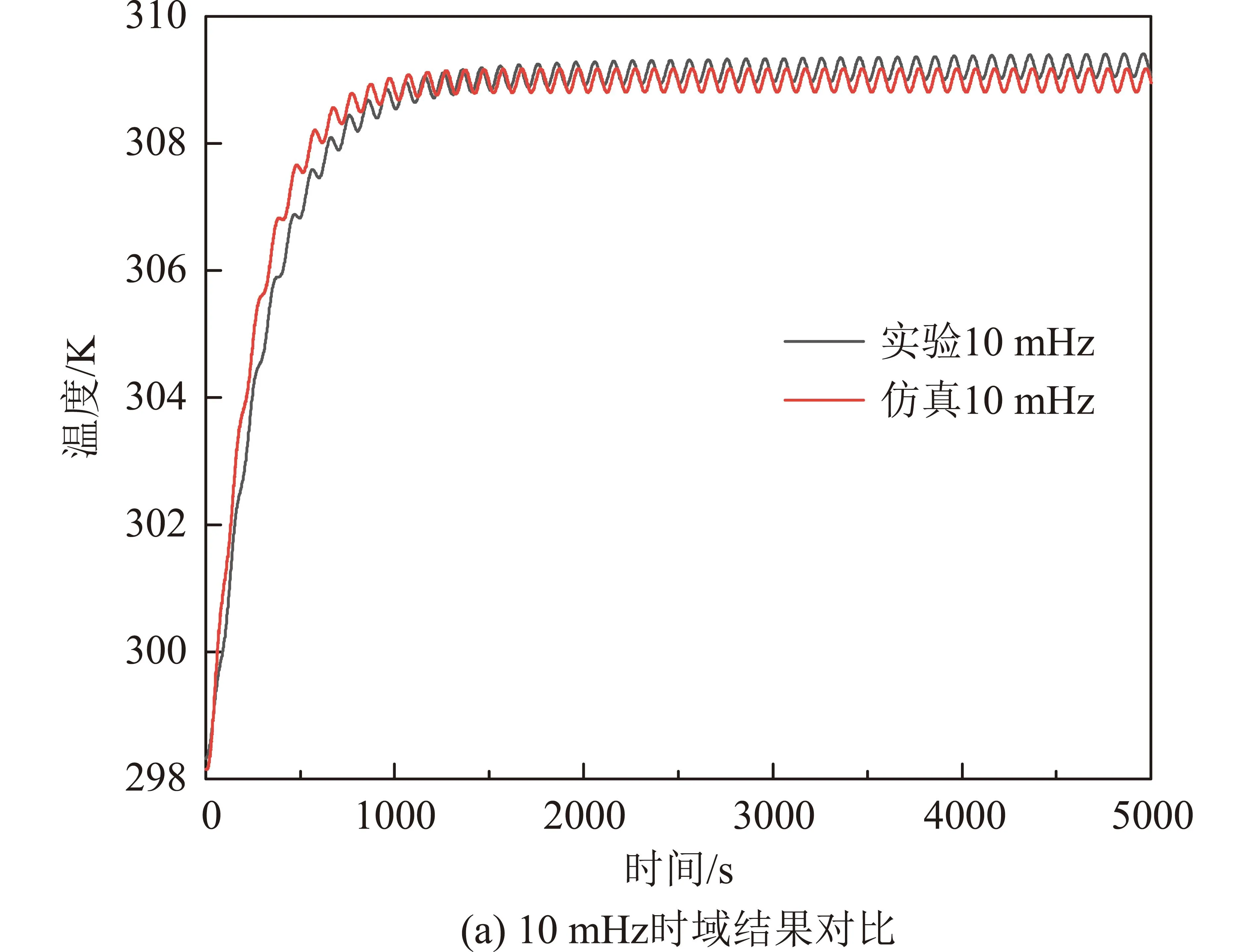
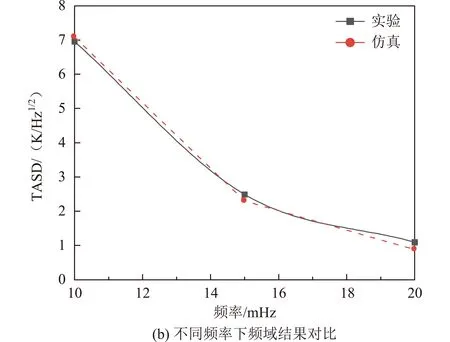
图3 试验与仿真结果对比 Fig.3 Comparison of experimental and simulation results

不同频率下的热流参数以及稳定时试验结果最大偏差见表2。从图3中可知仿真结果与试验结果一致,在时域上,温度升高趋势与试验一致,温度波动随频率的增加而减小,这一点在试验和仿真中都得到了体现。在频域中,试验中最大TASD的频率与仿真一致,且该频率与输入热流频率相同。以上结果表明,该模型可以用于分析温度噪声的影响。

表2 输入热流参数以及试验结果最大偏差Table 2 Maximum deviation of experimental results with different input heat flow parameters

2 结果与讨论

2.1 热源频谱特性对温度噪声的影响

引力波探测中温度噪声对频率敏感,首先研究单频热流波动的温度噪声传输。考虑星载引力波探测的空间环境条件,模拟了温度为4K的真空和无重力环境。被动热控材料为复合聚氨酯材料,辐射发射率为0.76,热导率为0.04W/(m·K),比热容为885.35J/(kg·K),密度为100kg/m3。输入热流参考“天琴”卫星科学试验阶段1入射太阳辐射[16](960～1314W/m2),由于本文是定性探究变化趋势和相关规律,因此不严格按照太阳热流的具体数值,假设

(7)

式中:Q为输入热流(W/m2);fj为热流频率(Hz),j=1,… ,n;图4中n=1,图5中n=50。

在单频热流条件下,热流、温度的时域和频域结果对比如图4所示。

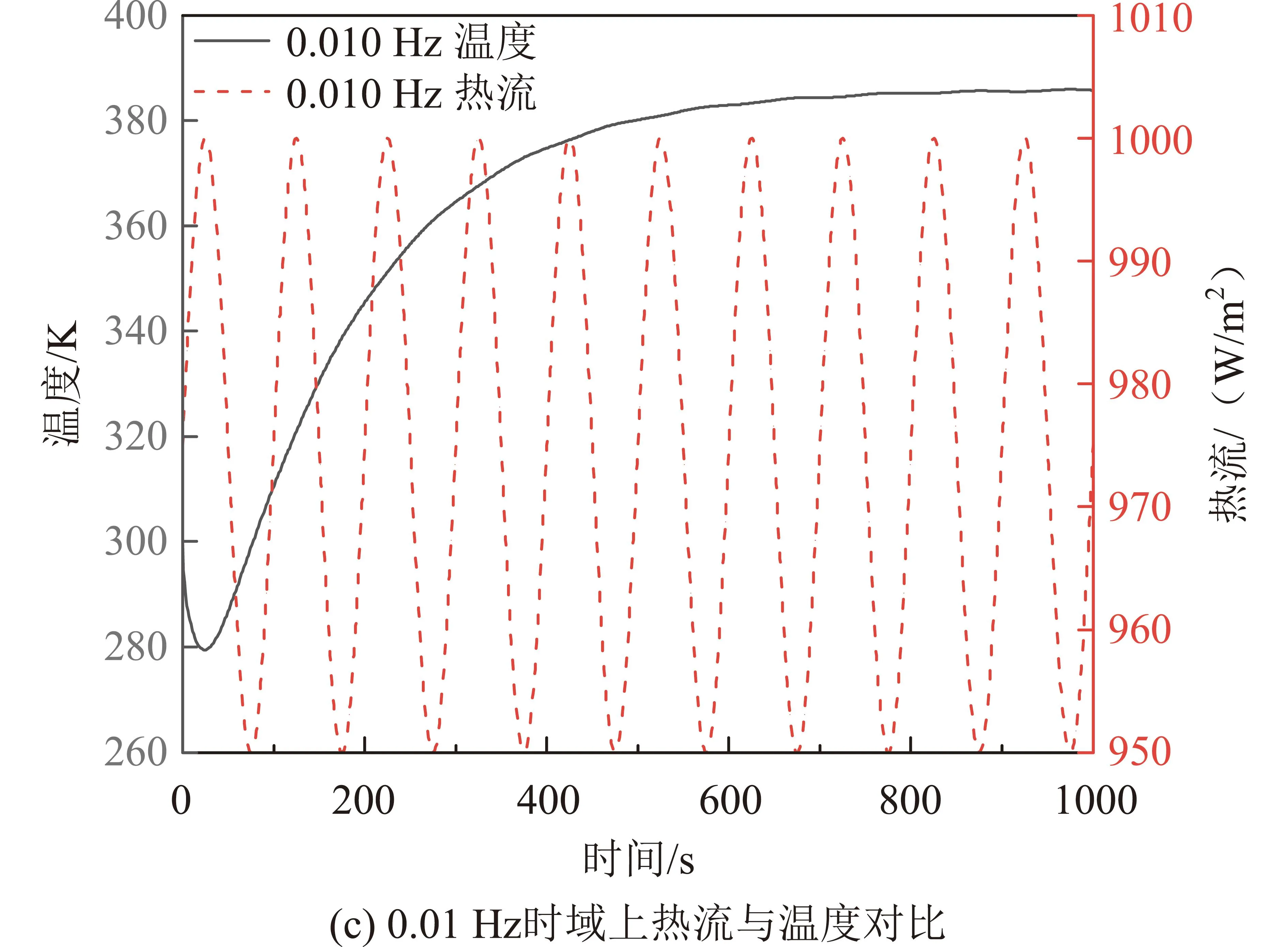
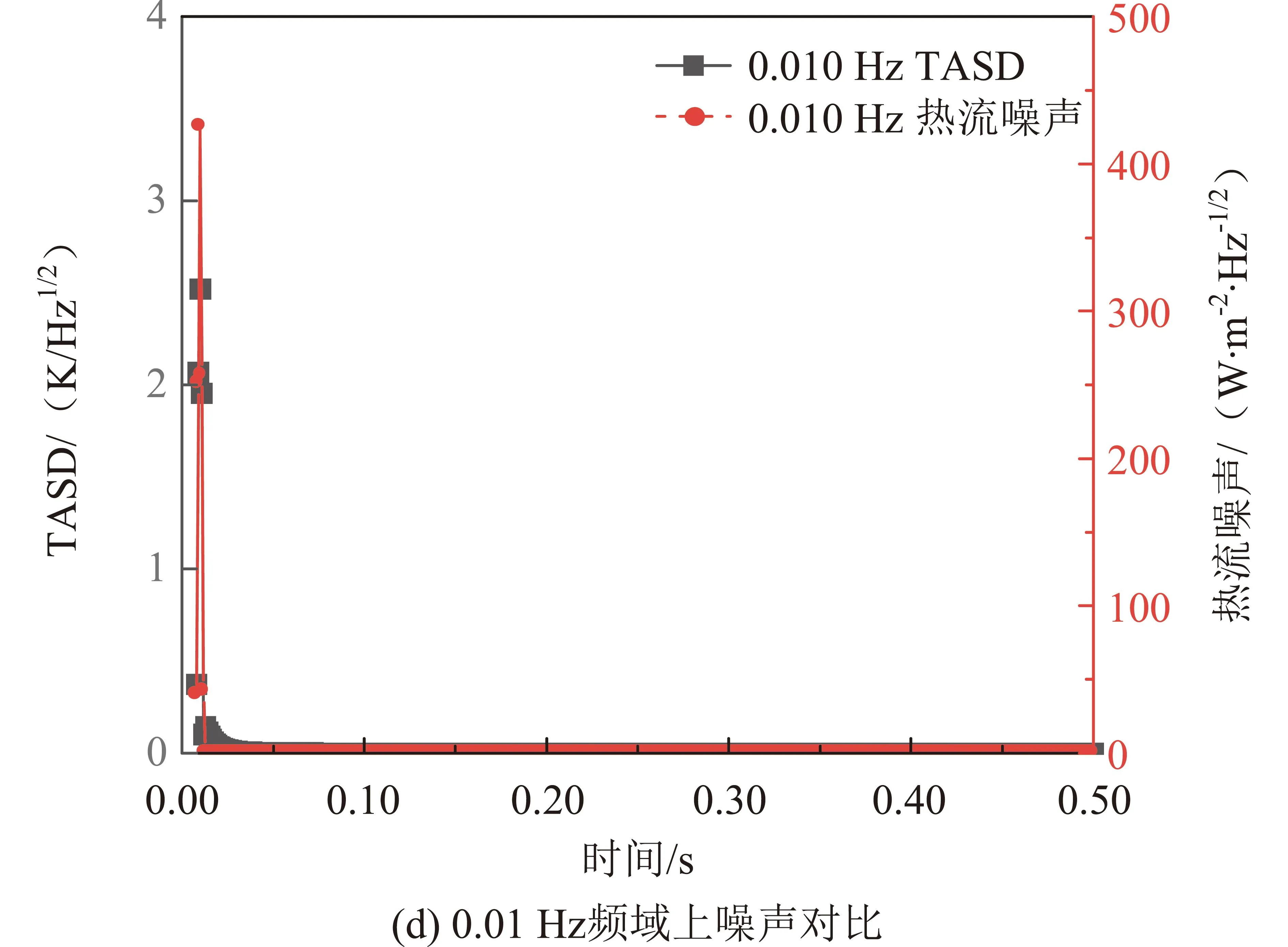
图4 单频热流和温度的时域和频域对比Fig.4 Comparison of heat flow and temperature fluctuation at mono-frequency in time and frequency domain

在时域上,温度波动频率与输入热流波动频率一致,见图4(a)(c),低频温度波动幅度(图4(a))比高频温度波动幅度(图4(c))更明显。输入热流幅值与温度幅值之比定义为[29]

(8)

式中:Qin为输入侧热流(W/m2);T1为输入侧温度(K);τ为热作用的波动周期(s)。由傅里叶导热定律可得

(9)

式中:T2为输出侧温度(K);L1为热控材料的厚度(m)。

由式(9)可知,当热流频率越大时,在热流波幅保持不变的时候,温度波幅就越小。通过对比图4(b)和图4(d)的频域振幅谱密度可以发现,在相同的热流振幅谱密度情况下,较高频率的温度振幅谱密度低于较低频率的温度振幅谱密度。

针对引力波探测中覆盖整个引力波敏感频段(0.1mHz～0.1Hz)的太阳辐射噪声频率,采用多频率正弦叠加的方法研究多频热源噪声对温度噪声传递的影响,取式(8)为输入热流,多频热流噪声和对应温度噪声的对比结果如图5所示,从图5(b)可以看出,随着噪声频率的增加,TASD逐渐减小,当频率超过0.17Hz时,TASD基本保持不变,结果表明,被动式热控材料在超低频段抑制温度噪声的能力较弱,而在高频频段抑制温度噪声的能力较强。针对这一特点,在较高频段采用被动热控材料;主动热控方法需要反应时间,较低频段意味着周期较长,采用主动热控方法抑制较低频段的温度噪声,通过针对不同频段的主被动方法结合,实现引力波全敏感频段的温度噪声控制。

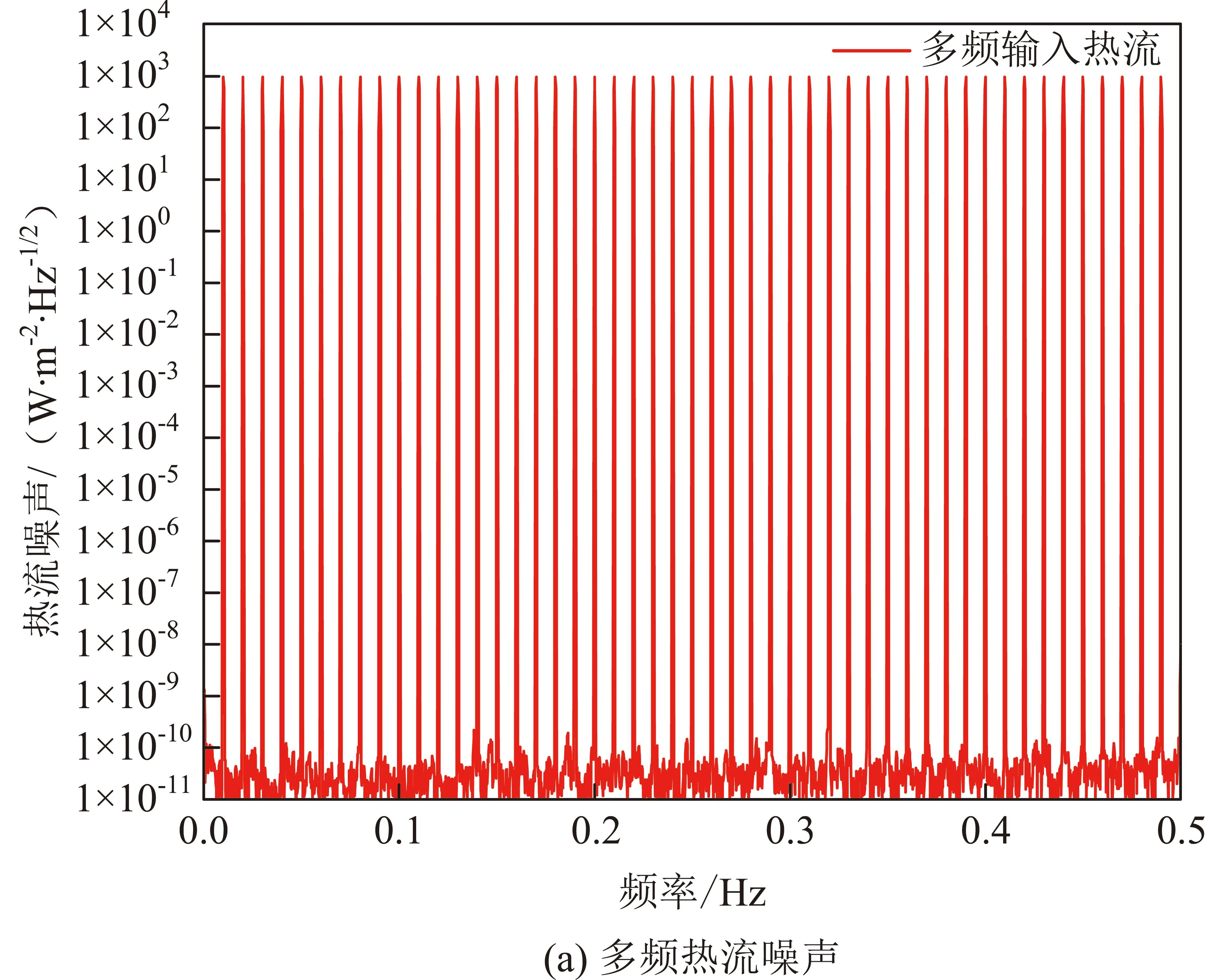
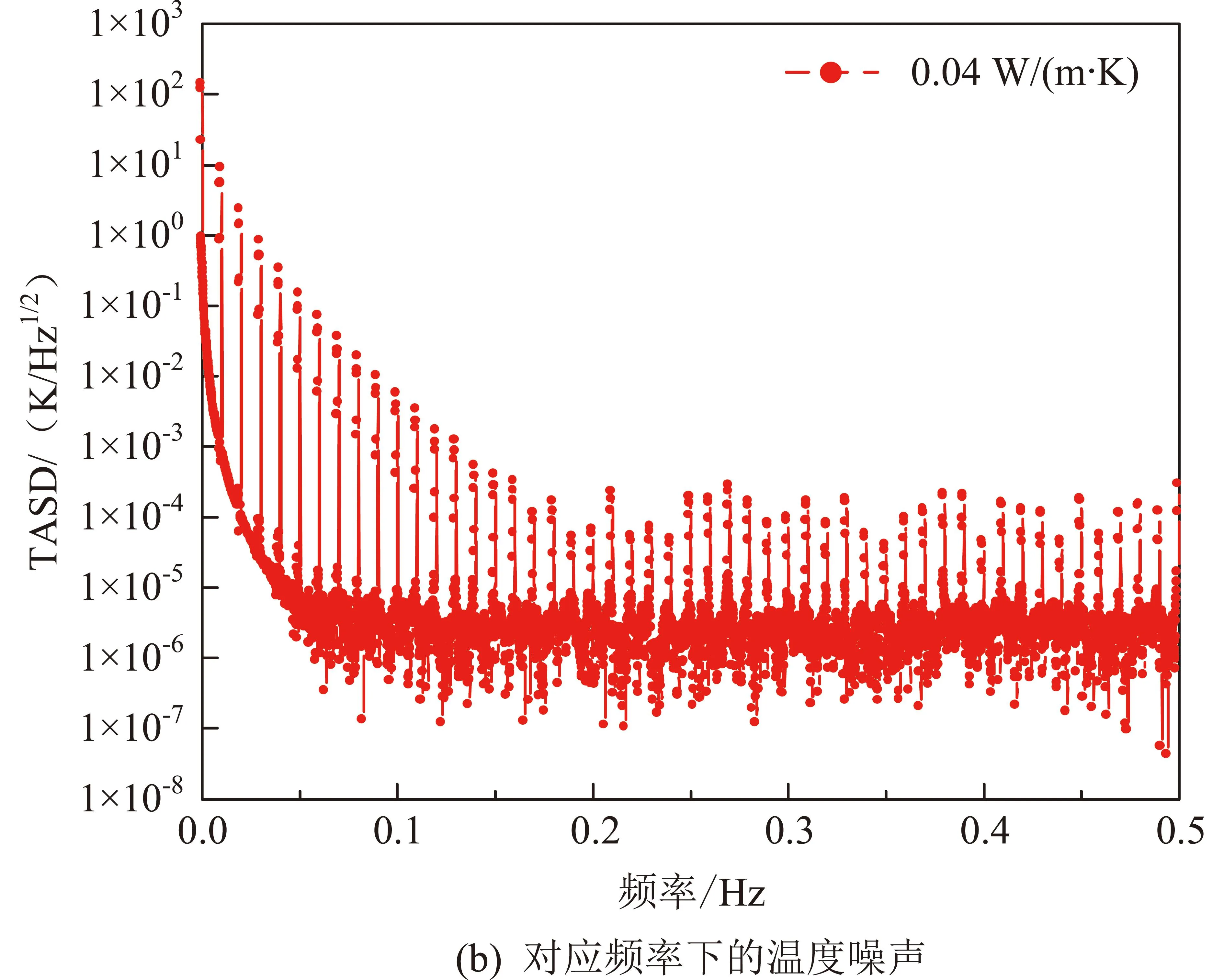
图5 多频热流噪声和对应温度噪声的对比Fig.5 Comparison of multiple frequency heat flow noise and temperature noise

2.2 厚度的影响

为探究被动热控材料不同厚度对温度噪声抑制的规律,厚度从1cm设置到6cm,保持被动热控材料的导热系数(0.04W/(m·K))和比热容(885.35J/(kg·K))不变,结果如图6所示。

对结果进行公式拟合,TASD随被动热控材料厚度变化的规律有

TTASD=ea+b×L+c×L2

(10)

式中:a,b,c为常数;L为被动热控材料的厚度(cm),具体数值参见表3。

表3 不同频率下的a,b,c参数值Table 3 a,b,c parameter values at different frequencies

图6 材料厚度对温度噪声的影响Fig.6 Effect of material thickness on temperature noise

从图6(a)中可以看出,增加热控材料的厚度可以降低温度噪声的强度,并且对于较高频率的温度噪声,抑制效果较明显,同时从图6(b)中可以发现,随着被动热控材料厚度的增加,温度噪声的对数呈线性下降,说明对于较低频率的温度噪声,需要采用更厚的被动热控材料进行抑制,对空间热控中的资源占用提出挑战。结合2.1节,对于超低频率的温度噪声,由于采用被动方法进行温度噪声抑制的效果有限,且需要占用更多的空间资源,因此需要考虑采用主动方法进行抑制。

3 结论

本文在时域结果的基础上进行频域温度噪声传递特性的研究,建立了基于温度振幅谱密度的低频温度噪声传递模型,通过试验验证了模型的准确性并进行了不确定性分析,通过该模型研究在引力波敏感频率下,热源频谱特性以及热控材料的厚度对温度噪声传递的影响,可得出以下结论。

(1)被动热控材料对不同频率的温度噪声抑制效果不同。随着噪声频率的增加,TASD逐渐减小,当频率超过0.17Hz时,TASD基本保持不变,说明被动热控材料对较高频段的温度噪声抑制效果好,针对较低频段的温度噪声可以采用主动热控方法。

(2)增加被动热控材料的厚度可以降低温度噪声的强度,并且对于较高频率的温度噪声,抑制效果较明显,温度噪声的对数随厚度的增加呈线性下降。对于超低频率的温度噪声,由于采用被动方法需要占用更多的空间资源,因此需要考虑采用主动方法进行抑制。