风电叶片粘接结构刚度退化模型

张 岩,徐嘉亮,安宗文,马 强

(1.甘肃省特种设备检验检测研究院,甘肃 兰州 730050) (2.兰州理工大学机电工程学院,甘肃 兰州 730050)

风电叶片作为整个机组转化风能的核心部件,占总成本的20%～30%[1-2],一旦损坏将会引发倒塔、电网烧毁等一系列恶性事故,造成巨大的经济损失[3-4]。丹麦Risø国家实验室的报告显示[5],导致叶片失效概率最高的事故是运行过程中粘接结构脱胶引发的叶片开裂。由此可知,风电叶片粘接结构影响着叶片的整体刚度和整体强度,叶片粘接结构的疲劳性能关系到叶片载荷能否顺利传递。

目前国内外学者针对风电叶片粘接结构疲劳失效问题已展开许多研究工作[6-7]。为了能够对风电叶片粘接结构的疲劳性能退化进行数值上的分析,以及更为直观地展现粘接结构在疲劳载荷加载作用下出现的多种损伤失效模式,Li等[8]分析了叶片粘接结构在疲劳载荷作用下裂纹的萌生与扩展规律,并且通过透射热成像技术研究了T字形截面的风电叶片粘接结构在疲劳载荷作用下的失效机理。Lahuerta等[9]将某34 m叶片上的粘接结构作为分析对象,通过试验以及理论分析的方法,深入研究了粘接结构在疲劳载荷作用下的刚度退化规律以及损伤机理。Liu等[10-11]基于此采用有限元分析方法进一步探讨了粘接层的强度、厚度以及宽度对叶片粘接结构力学性能的影响。黄吉[12]根据粘接结构疲劳失效过程中刚度退化规律,利用有限元方法进一步研究了挥舞摆振方向载荷对粘接结构力学性能的影响。Zamani等[13]将理论分析与有限元方法相结合对四点弯曲加载下粘接结构的疲劳寿命进行预测。Bayramoglu等[14]基于粘接结构损伤演化规律,利用有限元以及数值分析等手段,深入研究了粘接结构的破坏机理;寇海霞[15]通过理论分析与数值仿真模拟,以风电叶片粘接结构的刚度退化规律为切入点,分别对叶片粘接结构的静力特性和疲劳特新进行了详细分析,并建立了基于渐进损伤的叶片粘接结构刚度退化模型。

综上所述,现有的数值分析模型存在模型精度低以及模型参数需要通过大量试验获取等问题,这无疑给实际工程运用带来了巨大麻烦。鉴于此,本文基于复合材料层合板与粘接层的疲劳特性与粘接结构各失效模式的起始与演化,深入研究风电叶片粘接结构疲劳失效过程中的损伤演化规律。

1 粘接结构刚度退化模型建模

1.1 层合板刚度退化模型

层合板在疲劳载荷作用下剩余刚度退化规律与层合板损伤演化过程如图1所示,从图中可以看出层合板刚度退化规律与损伤演化规律相反,且刚度退化规律呈现出阶段性非线性的特点[16]。不同类型层合板使用的铺层材料以及铺层顺序不同,导致它们的疲劳寿命也不一样,但其在全寿命周期中各自的损伤演化规律是相似的。

根据这一现象选取相对载荷作用次数(n/N)为衡量疲劳损伤的自变量,则层合板疲劳加载过程中损伤量d可以表达为:

(1)

式中:n为载荷作用次数,N为对应载荷下的层合板疲劳寿命,D为以n/N为自变量的函数。

根据复合材料层合板的损伤演化规律,式(1)的边界条件描述如下。

材料未受损:

(2)

材料破坏:

(3)

在现有复合材料层合板疲劳损伤相关研究中,Miner线性损伤累积模型因为其表达式简单,使用限制条件较少等原因被广泛运用[17]。大量的层合板疲劳试验结果表明,层合板疲劳损伤的增长与加载过程中载荷作用次数n呈非线性的关系,但Miner线性损伤累积模型不能够准确地表达这一性质。因此,根据复合材料层合板的损伤演化规律[18],将层合板的损伤累积模型用指数函数形式表达为:

(4)

式中:A和B为模型参数,通过刚度退化疲劳试验数据确定。根据剩余刚度的退化规律[19]可将损伤d通过剩余刚度表示为:

(5)

式中:E0为初始刚度,E(n)为载荷作用n次时的剩余刚度,Ef为临界刚度。

式(5)的边界条件描述如下。

材料未受损:

(6)

材料破坏:

(7)

联立式(4)与式(5)得:

(8)

为了减小由层合板制造缺陷引起的误差,采用相对剩余刚度E(n)/E0来表达复合材料层合板在疲劳载荷影响下的剩余刚度。根据式(8),复合材料的相对剩余刚度可表示为:

(9)

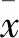
(10)

表1 玻璃纤维/环氧层合板试验参数

表2 玻璃纤维/环氧层合板刚度退化模型参数

由表2可知本文建立的层合板刚度退化模型具有较高的准确性,现将表2中的模型参数代入到式(9)中,得到玻璃纤维/环氧层合板的刚度退化曲线,如图2所示。在图2中的点代表玻璃纤维/环氧层合板在267.342 MPa以及297.076 MPa应力加载条件下的刚度退化试验数据,曲线是本文模型在267.342 MPa以及297.076 MPa应力下的刚度退化轨迹。

图2 玻璃纤维/环氧层合板刚度退化轨迹

1.2 粘接层刚度退化模型

通过对单搭接方式粘接层进行大量试验[21],得到其刚度退化规律如图3所示,从图中可以看出粘接层的刚度退化规律也呈现出非线性和阶段性的特点。

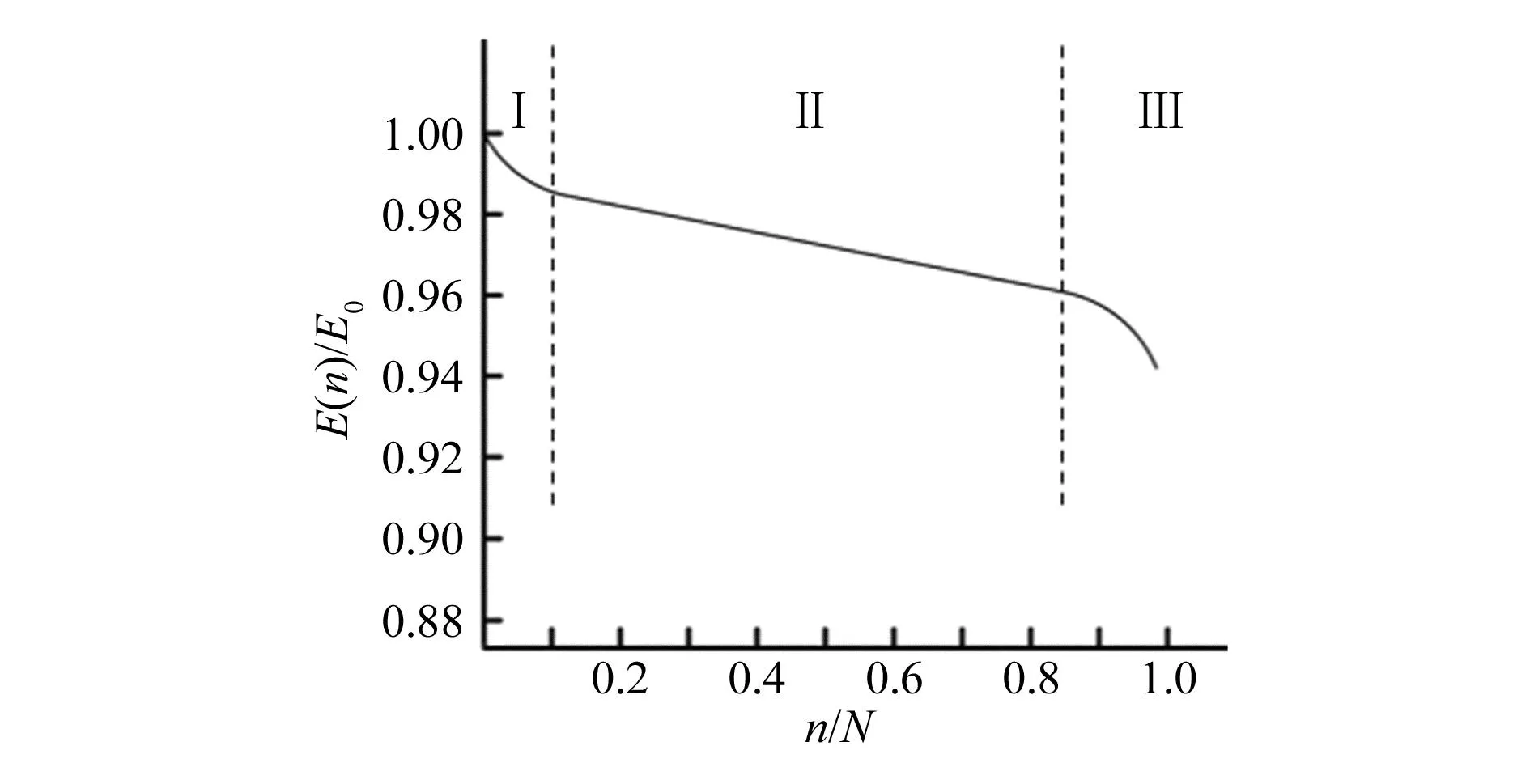
图3 粘接层刚度退化规律

影响粘接层刚度退化的因素有许多,其中粘接层的刚度退化速率和施加在其上的最大循环载荷与粘接层极限拉伸载荷之比相关[22]。如图4所示,从图中可以看出,随着施加载荷的增大,粘接层的刚度退化速率dE(n)/dn也随之增大,即:

(11)

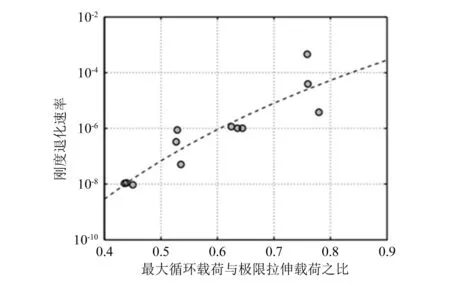
图4 不同载荷水平下的粘接层刚度退化速率

式中:F为最大循环载荷,Fu为粘接层极限拉伸载荷。

基于式(11)以及粘接层的刚度退化速率建立粘接层的刚度退化模型,即:

(12)

式中:g和h为模型参数。选取载荷作用次数n作为自变量来描述整个疲劳循环过程,但是在计算不同材料粘接层时,由于使用的结构胶不同,粘接层的寿命也不同,该模型可能无法准确描述使用不同材料的粘接层的刚度退化规律。通过分析结构胶的疲劳特性发现,虽然使用不同结构胶粘接后的粘接层的疲劳寿命不同,但是各损伤模式的起始与演化在粘接层全寿命中的周期相同。即不同材料粘接层虽然在相同循环载荷下造成的损伤不同,但是在相同载荷作用次数下的损伤相同。根据该结论可得粘接层的刚度退化模型为:

(13)

为了验证本文所建立的粘接层刚度退化模型的准确性,利用文献[22]中的粘接层疲劳试验进行验证。该文献以结构胶SikaDur330为研究对象,分别采用两种载荷水平在相同的试验条件下对试件进行加载,试验条件见表3。基于文献[20]中的试验数据以及表3,利用最小二乘法对式(13)中的数据进行拟合,得到相关模型参数以及平均误差,见表4。

表3 SikaDur330结构胶试验参数

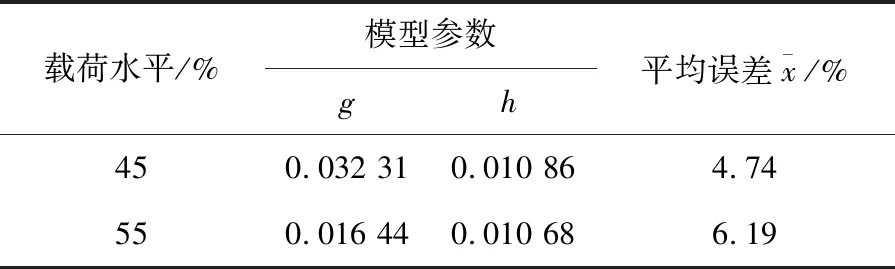
表4 SikaDur330结构胶模型参数

由表4可知,本文建立的层合板刚度退化模型具有较高的准确性,现将表4中的模型参数代入式(13)中,得到结构胶SikaDur330的刚度退化曲线,如图5所示。在图5中点代表结构胶SikaDur330在45%以及55%应力加载条件下的刚度退化试验数据,曲线是本文模型在45%以及55%应力下的刚度退化轨迹。

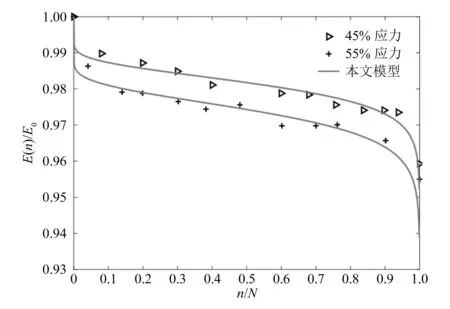
图5 玻璃纤维/环氧层合板刚度退化轨迹

1.3 风电叶片粘接结构刚度退化模型建模

风电叶片粘接结构在疲劳载荷影响下的刚度退化由层合板刚度退化和粘接层刚度退化两个部分组成。图6所示为叶片粘接结构模型,设上粘接层合板在整个粘接结构中刚度分布系数为p,下粘接层合板在整个粘接结构中刚度分布系数为q,粘接层在整个粘接结构中的刚度分布系数为t。

图6 疲劳加载试验试件

结合本文提出的复合材料层合板刚度退化模型(式9)以及粘接层刚度退化模型(式13),则风电叶片粘接结构刚度退化模型为:

(14)

式中:E01和Ef1为上粘接层合板的初始刚度和临界刚度,E02和Ef2为下粘接层合板的初始刚度和临界刚度。对式(14)合并同类项可得:

(15)

2 风电叶片粘接结构刚度退化模型验证

2.1 风电叶片粘接结构疲劳试验

为了验证本文所建立粘接结构刚度退化模型的准确性,本文以文献[23]中Beam18试件为分析对象,为了尽可能地提高结构胶的黏附力,在粘接前将层合板上的粘接面进行抛光和超声波清洗,然后采用结构胶将制作好的梁帽与腹板进行粘接,之后将完成粘接工序的工字梁在60 ℃的环境下固化2 h。该试验是在常温常压的环境中进行,工字梁粘接结构在MTS800标准伺服液压机上以四点弯曲疲劳加载的方式进行试验,试验条件见表5。

表5 Beam18粘接结构试验参数

2.2 相关文献刚度退化模型

从宏观唯象的角度入手,基于连续介质损伤理论建立一种能够准确地描述风电叶片粘接结构在循环载荷下刚度退化规律的剩余刚度模型[15],如式(16)所示:

(16)

式中:σmax(n)为循环载荷作用下粘接层所受的最大应力;εmax(n)为循环载荷作用下粘接层应变最大值;a和b为模型参数,决定着层合板刚度退化过程中刚度退化曲线的退化量和退化速率。

虽然该粘接结构刚度退化模型的适用性与准确性已通过试验数据验证,但是该模型只是利用数值拟合的方式在刚度退化模型中表达出粘接层在疲劳载荷作用下对整个粘接结构刚度退化过程的影响,并没有将粘接层在疲劳载荷作用下刚度退化规律以及刚度退化过程中各阶段刚度退化曲线的退化量和退化速率直接表达出来。同时,该模型中循环载荷作用下粘接层所受的最大应力σmax(n)以及循环载荷作用下粘接层应变最大值εmax(n)需要通过仿真或试验的形式求出,这给实际工程应用带来了巨大的麻烦。

2.3 粘接结构刚度退化模型验证

根据表5以及式(15)和式(16),采用最小二乘法拟合得到本文建立的工字梁粘接结构的刚度退化模型与文献建立的工字梁粘接结构的刚度退化模型的相关参数及误差,见表6。

表6 粘接结构刚度退化模型参数

基于表6以及试验数据,分别得到Beam18工字梁粘接结构在循环载荷作用下通过式(15)以及式(16)计算得到的刚度退化轨迹图。在图7中点代表Beam18工字梁粘接结构在应力最大峰值为62.3 kN加载条件下的刚度退化试验数据;浅色曲线是采用本文模型计算出的刚度退化轨迹,深色曲线是通过文献模型计算出的刚度退化轨迹。

图7 Beam18两种模型计算的刚度退化轨迹

经过上述周密的验证过程,由图7和表6可知本文所建立的风电叶片粘接结构刚度退化模型能够精确地拟合文献[23]中的试验,且平均误差为0.13%,证明该模型具有较高的准确性。其次相较于文献[15]中所建立的模型,本文所建立的模型能够更好地通过数值形式表达粘接层在疲劳载荷影响下其刚度退化过程,从表6中的平均误差可以看出本文所建立模型的平均误差相比文献[13]中所建立模型的平均误差小,证明了本文所建立模型的优越性。

3 结束语

通过对比分析现有的复合材料层合板以及粘接层刚度退化模型,建立疲劳载荷作用下的层合板以及粘接层刚度退化模型,根据风电叶片粘接结构在疲劳载荷作用下的刚度退化规律,将层合板以及粘接层的刚度退化模型相结合,建立了能够表达风电叶片粘接结构疲劳载荷作用下损伤演化规律的刚度退化模型。利用相关文献中工字梁粘接结构疲劳试验数据以及粘接结构刚度退化模型对本文所提出模型的准确性和优越性进行验证。从验证结果可以看出,相较于现有的粘接结构刚度退化模型,本文所建立的模型能够准确描述粘接结构在疲劳载荷作用下的损伤演化规律,且该模型与试验数据之间的平均误差要比文献中的模型要小,具有更高的模型精度,为深入研究风电叶片粘接结构疲劳失效提供了理论基础。