两操作模式2-R(SS)2-R(RR)2(RR)2并联机构运动学分析与优化设计
张宇轩,汪满新,黄兴锋,安守和
(南京理工大学机械工程学院,江苏 南京 210094)
由外转动副驱动、含平行四边形支链的并联机器人因从动臂可用碳纤维制成轻杆,驱动装置固定安装在机架上,可有效减轻末端负载,故可使末端动平台获得很高的速度和加速度[1],已被广泛应用于食品医药、现代物流等自动化生产线中,用于轻小散乱物料抓取、分拣、搬运等作业[2]。
可实现三平一转的高速并联机器人[3]是目前应用最广的高速并联机器人机构类型,可满足标的物需要SCARA运动的场合,但在标的物不需姿态调整的应用场合,仅需使用3自由度平动并联机器人[4]即可满足要求,而在平面内即可完成标的物分拣、抓放和搬运作业的应用场合,则仅需使用2自由度平动并联机器人[5]。从提升机构应用效果来看,机构所具有的自由度与目标任务所需自由度数目和类型相匹配是最理想的,这样可以依靠机构自身约束力去承担非任务自由度方向的载荷,有利于提高机构自身约束方向的使用效率,也可使机构具有更好的刚度和精度。然而,现有高速并联机器人机构大多操作模式固定,不具备根据现场任务的自由度变化要求进行构型重构的能力,而同时使用多台高速并联机器人机构又将带来成本的提升[6]。
多操作模式高速并联机构定义为具有多个不同操作模式的高速并联机构,其特点是通过合适的控制,可以使机构转入不同的操作模式,实现自由度数目或性质的改变,故可满足根据现场任务所需自由度的变化进行构型重构的要求[6]。多操作模式并联机构主要包含运动分岔并联机构、变胞并联机构、含可分离/可连接部件的并联机构等。如安守和等[7]基于制动器放开或锁死中间支链中的转动叉与静平台间的转动副,提出一种具有两种操作模式的高速并联机器人机构,该机构可在任意位形下快速切换操作模式。
运动学分析与优化是并联机构设计最重要的研究内容之一,近年来,众多学者在运动学性能评价指标构造、优化设计方法等方面开展了大量研究工作[8-11]。如Gosselin等[8]提出了以雅可比矩阵条件数的倒数作为优化机构尺度参数的运动学性能评价指标。汪满新等[9]利用矩阵变换得到了一种具有齐次量纲且与坐标系选取无关的解耦雅可比矩阵,进而据此构建了运动学性能指标,完成了一种三自由度并联机构的优化设计。值得注意的是,以往针对并联机构尺度优化设计的研究对象主要为单一操作模式的并联机构,对于多操作模式并联机构,由于不同操作模式共用一套尺度参数,故还需考虑如何兼顾不同操作模式下机构的运动学性能。
本文以2-R(SS)2-R(RR)2(RR)2两操作模式高速并联机构为对象,分析该机构的自由度,构造运动学性能评价指标,进而统筹考虑两种操作模式,研究可使机构全域运动学性能最优的尺度优化设计方法,以期为具有多种操作模式的机构优化设计提供重要参考。
1 机构简介及自由度分析
图1为2-R(SS)2-R(RR)2(RR)2两操作模式并联机构的3D造型,它由静平台、动平台以及3条支链组成。其中第一条和第二条支链的结构均为R(SS)2,包括一条主动臂和两条平行且相等的从动臂;第三条支链的结构为R(RR)2(RR)2,包括转动叉、主动臂、辅助臂、肘架、三条平行且相等的从动臂,肘架同时与主动臂、辅助臂、3条从动臂转动连接,且肘架与其中两条从动臂相连的转动轴线和肘架与主动臂相连的转动轴线共线。在此,()2表示平行四边形结构,S表示球副,R表示转动副。第一、二支链中与静平台连接的R副为驱动副,第三支链中主动臂和转动叉之间的R副为驱动副。为实现该机构在两种操作模式下切换,第三支链转动叉末端设有制动器,制动器固定端与机架相连,以控制转动叉锁死或转动。该机构的两种操作模式如下:1)3自由度模式,此时转动叉可转动,末端动平台具有沿u轴和w轴平动及绕w轴转动3个自由度;2)2自由度模式,此时转动叉被锁死,其他结构不变,末端动平台具有沿u轴和w轴平动2个自由度。值得注意的是,在2自由度模式下,因该机构有3个驱动副而仅有2个自由度,故为冗余驱动机构。本机构可应用在需切换操作模式的场合,例如,在某物料分拣线上包含异常物料分辨装置,若是正常物料,只需利用该机构的两平动将物料传输至下一个工位,若是异常物料,则需通过两平一转运动将异常物料送至一固定箱子中或其他工位。

1—动平台;2—第一从动臂;3—第一主动臂;4—肘架;5—辅助臂;6—第三主动臂;7—转动叉;8—静平台;9—第二主动臂;10—第二从动臂;11—第三从动臂
图2所示为2-R(SS)2-R(RR)2(RR)2两操作模式并联机构的结构简图,图中点Ai(i=1,2,3)为第i条支链与静平台相连转动副中心,并构成三角形△A1A2A3,点Ci(i=1,2,3)为第i条支链与动平台相连的铰链中心点,并构成三角形△C1C2C3。为使机构简图直观简洁,将第三支链用图2所示的方法进行了简化,显然该简化不会改变支链的运动特性。为方便后文描述,在△A1A2A3和△C1C2C3上分别建立了固定坐标系{R}和动平台连体系{R′},其中固定坐标系{R}原点O在A1A2的中点上,且有x⊥△A1A2A3和y⊥OA3;动平台连体系{R′}原点O′在C1C2的中点上,且有x′⊥C1C2和z′⊥△C1C2C3。如图2所示,为方便描述机构运动形式,以点A3为原点建立坐标系A3-uvw,其中w轴与z轴重合,v轴与第三支链中主动臂和转动叉相连的R副轴线重合,因此u轴和w轴始终与第三支链共面。

图2 2-R(SS)2-R(RR)2(RR)2机构
两种操作模式下第一、第二支链结构相同,且均为典型的R(SS)2支链,故其末端自由度为沿u轴、v轴、w轴的平动和绕w轴的转动,则其自由度{L1}、{L2}可分别表示为:
{L1}={R(A1,w)}{T}={R(O,w)}{T}
(1)
{L2}={R(A2,w)}{T}={R(O,w)}{T}
(2)
式中:R(Ai,w)表示过点Ai且与w轴平行的轴线的转动,{T}表示三维平动,{R(O,w)}表示过点O且与w轴平行的轴线的转动。

(3)
式中:{T(u)}、{T(w)}分别表示沿u、w方向的移动自由度。
综合考虑3条支链,可得在第一种操作模式下2-R(SS)2-R(RR)2(RR)2机构的自由度{L1}为:
{R(O,w)}{T(u)}{T(w)}
(4)
由式(3)可知,第一种操作模式下机构自由度数为3,包括沿u轴、w轴的平动和绕w轴的转动。

{T(u)}{T(w)}
(5)
因此,第二种操作模式下机构自由度数为2,即沿u轴、w轴的平动。
2 运动学性能评价指标
机构在3自由度操作模式下,动平台可绕竖直z轴(即w轴)转动,因此动平台连体系{R′}相对于固定坐标系{R}的姿态矩阵R可表示为:
(6)
式中:α4为第三支链转动叉绕z轴的旋转角度。
当机构处于2自由度操作模式下,机构没有绕z轴转动的自由度,α4为一定值。故在以下分析中,可先假设该机构处于3自由度操作模式下,然后将α4设为某一定值,如α4=0,则可得到2自由度操作模式下的运动学模型。
如图2所示,点O′在固定坐标系{R}中的位矢r=[xyz]T,r可表示为:
r=ai+Liui+liwi-cii=1,2,3
(7)
式中:ai和ci分别为点O到点Ai和点O′到点Ci的位矢,ui和wi分别为第i支链主动臂AiBi和从动臂BiCi的单位方向矢量,li和Li分别为第i条支链从动臂和主动臂杆长。
ui=[cosαisinαi0]Ti=1,2
u3=[sinα3cosα4sinα3sinα4cosα3]T
(8)
式中:αi为第i条支链主动臂转角。
对式(7)求导,得:
(9)

(10)

(11)
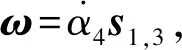
(12)
Jxa1=[(w1+A1)T(w2+A2)T(w3+A3)T]T
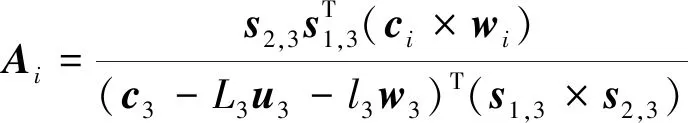
i=1,2
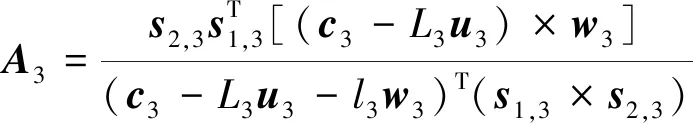

(13)
(14)
式中:V1为第一种操作模式下机构作业空间的体积。

(15)
其中:
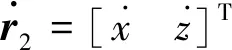

3 运动学性能分析
3.1 尺度参数归一化
根据2-R(SS)2-R(RR)2(RR)2并联机构两种操作模式运动特点,第一种操作模式工作空间为一扇环体区域,其内径为ra、宽为r、高为2h,转角范围为αz,其中空间下平面距离xy面为h,如图3所示。而第二种操作模式机构不能绕z轴旋转,取αz恒为零,故其工作空间为扇环体区域在xz平面的截面,如图4所示。

图3 第一种操作模式工作空间

图4 第二种操作模式工作空间
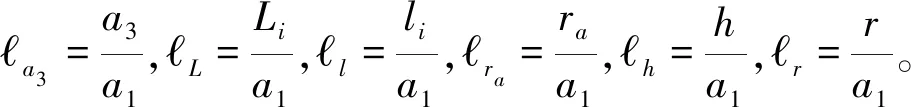
因为第三支链伺服电机和减速器安装在转动叉上,故转动叉中心轴线与静平台之间应留有足够的安装尺寸,且防止转动叉尺寸过大,故设定
δmax≥a3≥δmin
(16)
式中:δmax、δmin分别为伺服电机和减速器安装位置系数的最大值、最小值,由电机和减速器大小决定。
此外,并联机构各零件尺寸应满足装配条件的要求,机构末端应能到达给定工作空间边界位置,设定如下尺度约束:
(17)
3.2 尺度参数对运行性能的影响规律
借助单调性分析法揭示尺度参数对不同操作模式下机构运动学性能的影响规律。为了便于对机构尺度参数进行分析,考虑工程实际设计需求,给定-30°≤αz≤30°、h=0.8和r=0.6,且不失一般性,设定上述归一化后的尺度参数变化范围如下:0.2≤a3≤1,3.4≤L≤4.2,4≤l≤6,2.6≤ra≤3.6。

图随尺度参数L、ra、a3、l的变化规律
4 优化设计
为使机构在两种操作模式下均具有良好的运动学性能,需以两种操作模式的条件数均值和标准差作为优化设计目标:
(18)
式中:n1、n2分别为两种操作模式工作频率占比,s1、s2分别为条件数均值和标准差的比重。不失一般性,在此可假设n1=n2=1,s1=s2=1。
考虑式(16)和式(17)的装配约束,可将两操作模式并联机构运动学优化问题表示如下:

图随尺度参数L、ra、a3、l的变化规律
(19)
其中:
x=[a3lLra]T
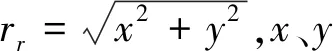
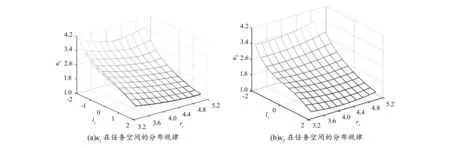
图9 κ1和κ2在任务空间的分布规律
5 结束语
本文提出一种具有两种操作模式的新型并联机器人机构,并借助位移子群及其运算分析了不同操作模式下机构的自由度。基于矢量法建立了2-R(SS)2-R(RR)2(RR)2两种操作模式并联机构统一的速度映射模型,并据此构造出两操作模式并联机构局部和全域运动学性能评价指标,揭示了尺度参数对不同操作模式下机构运动学性能的影响规律。统筹考虑两种操作模式,将机构运动学优化设计归纳为多目标有约束优化设计问题,并通过算例得到一组可使机构具有良好运动学性能的尺度参数。

