抽水蓄能6+6 长短叶片机组对厂房振动的影响研究
向 明,李海玲,赵聚平,杨 晖,杨 恒
(1.国网新源湖南黑麋峰抽水蓄能有限公司,湖南省长沙市 410007;2.中国水利水电科学研究院,北京市 100048)
0 引言
抽水蓄能电站具有高水头、高转速、双向运转、过渡过程复杂等特点,机组振动诱发的厂房结构振动问题较常规电站更为突出。近年来,国内已建成运行的多座抽水蓄能电站陆续出现厂房强烈振动现象,如张河湾、蒲石河抽蓄电站厂房局部构件振动偏大和噪声超标[1-6]、广蓄电站楼板出现裂缝等[7,8],个别电站在部分运行工况下产生的振动和噪声甚至影响到周边居民。黑麋峰抽水蓄能电站投产以来,存在机组并网需预开启多对小导叶、部分工况振摆偏大以及过渡过程等遗留问题,并且电站在过渡过程及部分运行工况下厂房局部有较强烈的振感,也引发上库输水管道途经区域的居民楼产生振动和噪声[9]。
为了优化机组的水力性能,更好地保障机组和厂房的安全稳定运行,黑麋峰抽水蓄能电站对4号机组进行了水力优化,重新设计并更换了转轮。更换后的水泵水轮机转轮为6+6 长短叶片(原机组为9 叶片转轮),座环20 个固定导叶,20 个活动导叶,该机组是世界首台应用的6+6 长短叶片转轮蓄能机组;额定转速nr300.0r/min,飞逸转速np465.0r/min;最大扬程为335.0m,最低扬程为272.8m。
本文建立了黑麋峰抽水蓄能电站4 号机组厂房结构的三维有限元模型,基于机组改造前后不同压力脉动特性,计算分析了厂房局部结构的自振频率特性和机组振动载荷、脉动压力荷载作用下的动力响应,研究不同转轮特性机组对厂房引起的不同激励响应特性,为未来抽水蓄能电站的设计、建设、运行和改造提供参考。
1 厂房结构有限元模型和计算方法
1.1 材料参数
电站4 号机组段的厂房楼板上下游尺寸为25.50m,左右宽22.98m;蜗壳进口直径为2.80m;母线层层高为6.20m,水轮机层层高为6.00m;发电机层楼板厚度0.75m,母线层楼板厚度0.63m,水轮机层楼板0.83m。
电站主厂房各种材料力学参数见表1。机组设备转动惯量见表2。
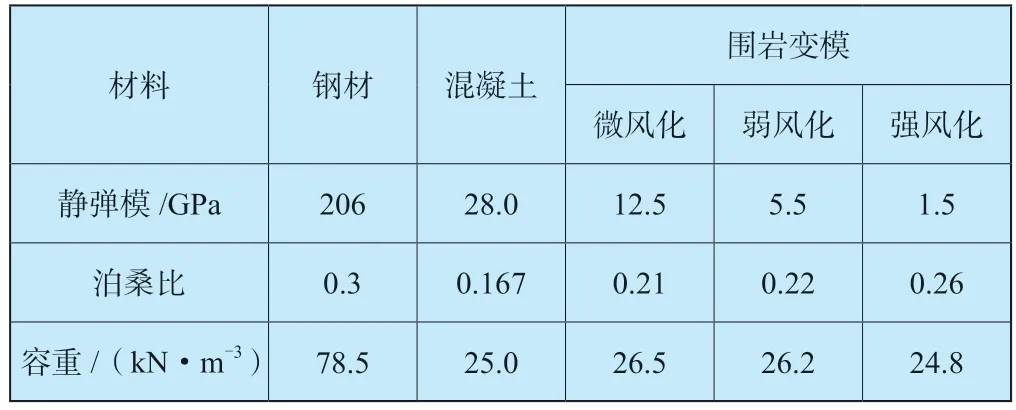
表1 材料力学参数Table1 Material parameters
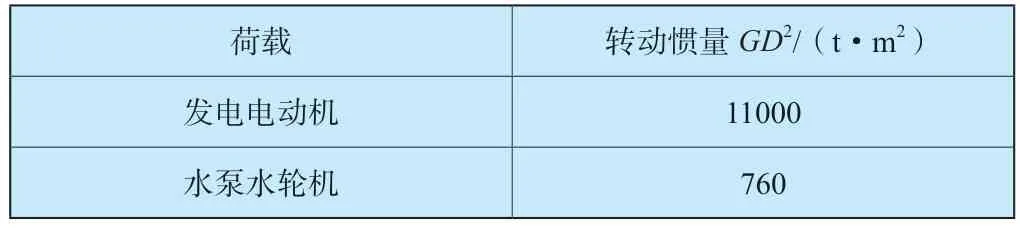
表2 机组设备转动惯量Table 2 Rotational inertia of unit
1.2 有限元模型及参数取值
1.2.1 振源分析
对于抽水蓄能电站的厂房振动而言,其振源有水力振源、机械振源和电磁振源3 种,且一般以水力振源为主。通过对转轮改造前、后的4 号机组脉动压力开展测试,不同出力工况下各部位脉动压力统计见表3。
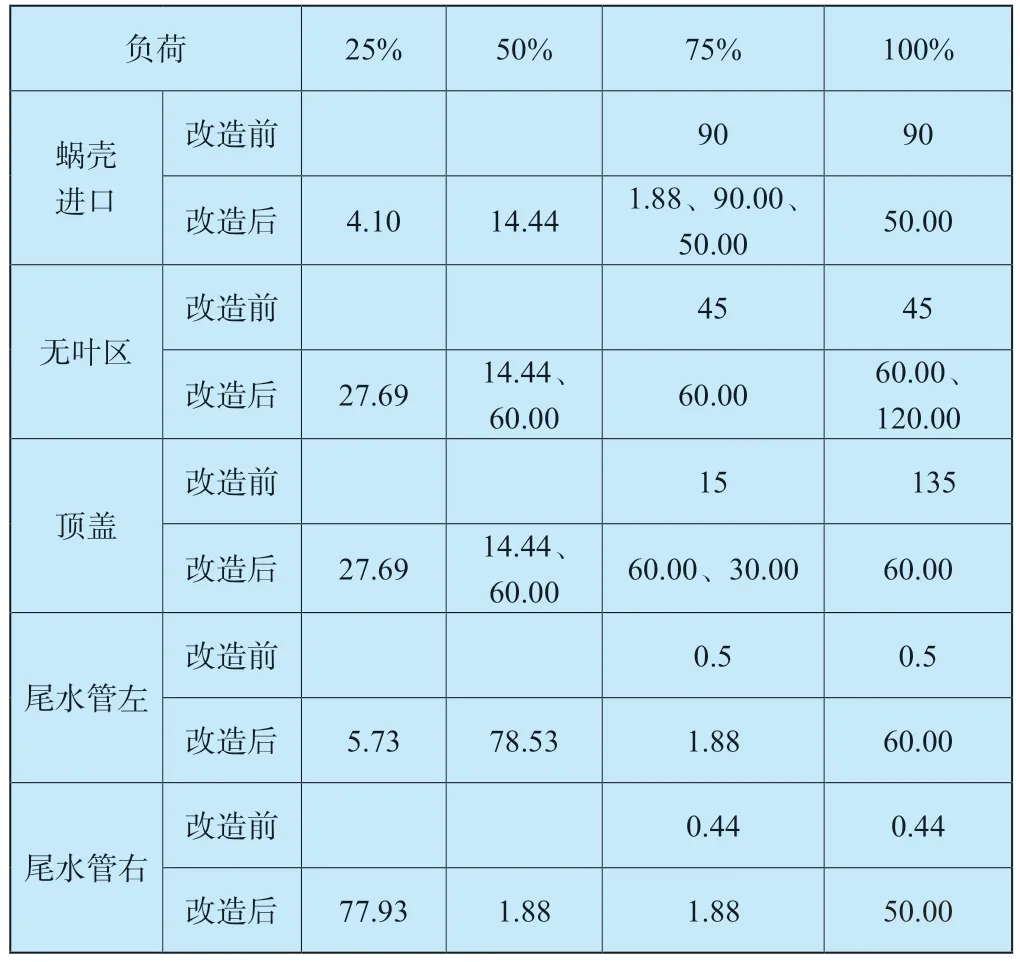
表3 4 号机组改造前后脉动压力主频统计表Table 3 Basic frequency of pulsating pressure of unit 4 Hz
机械振源即为机组旋转部分安装偏心引起的偏心力,其频率一般为机组的转频(本电站为5.0Hz)。随着机组安装工艺的不断提升,机械振源所占比重不断下降,甚至可忽略不计。电磁振源主要为不平衡磁拉力,其频率为50Hz 及其倍频(100Hz 等),但其振动能量相对水力振源也较小[10,11]。因此,在计算时,把脉动压力作为振源进行分析计算。
1.2.2 有限元模型
计算中,为了保证计算模型的可靠性,对于混凝土结构,全部采用三维实体单元。对于楼板、梁、柱子、楼梯、风罩等结构,严格按照设计尺寸模拟。在不影响上述结构计算结果的工程精度基础上,不模拟一期大体积混凝土的廊道等部位。流道结构采用壳单元进行模拟。弹簧阻尼单元用于模拟围岩对厂房的约束。对于机组、轻体墙等采用附加质量模拟。主厂房模型坐标系选取如下:X轴为机组轴线,正向为4 号机组指向安装间;Y轴垂直机组轴线,正向指向上游;Z轴正向为垂直向上。厂房三维CAD 模型以及有限元网格模型见图1,网格节点数209886 个。

图1 4 号机组段厂房结构有限元网格(含边界)Figure 1 Finite element gridding of power plant of unit 4 section(with boundary included)
就该电站而言,其围岩岩性主要为Ⅱ类花岗岩。考虑到动力分析计算规模,参照小浪底围岩抗力试验成果以及国内其他水电站厂房振动研究成果,计算模型采用黏弹性边界模拟周边约束条件,具体如下:围岩法向抗力系数取80kg/cm3,切向取法向的一半,厂房段法向抗力系数取20kg/cm3。
2 振动响应计算分析
2.1 计算分析条件
根据4 号机组改造前后甩负荷试验前的稳态脉动压力脉动主频数据(见表3),开展了75%出力和100%出力两个工况下的计算分析。此外,电站4 号机组改造前后的厂房振动测试表明,厂房主要振源为水力振源,因此本次计算分析不考虑机械力和电磁力。
本次计算分析厂房结构响应,采用Newmark 逐步积分法在时域内求解线弹性动力平衡方程:
式中:M——结构的质量矩阵,kg;
C——结构的阻尼矩阵;
K——结构的刚度矩阵;
V——各自由度的位移向量,m;
F——等效节点力,N。
综合考虑模型的规模、计算机的能力和脉动荷载的频率特性,在保证结果可靠的前提下,选取的荷载持续时间为5s。此外,参考笔者之前做过的国内类似电站的计算分析,厂房结构的阻尼比ξ取0.02。在结构岩体体系动力反应中,能够兼顾计算精度和计算效率的方法才易于被工程接受。黏弹性人工边界虽然只有一阶精度,但其算法有良好的稳定性,物理概念简单明确,易于有限元编程实现的特点使其有较强的吸引力。因此,本项目采用黏弹性人工边界模拟岩体辐射阻尼效应,并采用柱面波模拟岩体中远域能量逸散的散射波。
极坐标下出平面波的运动方程可表示为:
式中:w——出平面位移;
r——波源到计算点的距离;
cs——剪切波波速。
式中:G——剪切模量;
ρ——介质密度。
对于从坐标原点射出的柱面波,可以采用如式(4)形式的解:
式中:w——位移,m;
r——波源到计算点的距离,m;
cs——剪切波波速,m/s。
任一点的速度可以表示为:
式中:G——剪切模量,Pa;
f′——f对括号内变量的导数。
将式(4)和式(5)带入到式(6)中,可得任一半径rb处以矢径为外法线的单元面上应力与该处速度和位移的关系,如式(7)所示:
式(7)的物理意义是在半径rb处截断介质,并在截断的边界上布置一系列的每单位面积阻尼系数为Cb的阻尼器和刚度系数(即抗力系数)为Kb的线性弹簧,其中:
本次动力响应计算分析的抗力系数按上述1.2.2 中的参数取值,并假设散射波为压缩波。计算分析以下结构的振动响应:①三层楼板;②三层机墩;③两层立柱。
2.2 楼板振动响应计算分析
不同频率脉动压力作用下,三层楼板振动响应最大值分别统计于表4,由于篇幅所限,这里只列出4 号机组改造前后发电机层振动响应幅值变化,见图2 和图3。从数据中可以看出:各工况下,三层楼板竖向(Z向)振动响应总体比水平向振动响应大。相同出力工况下,与4 号机组改造前脉动压力作用下三层楼板总体振动响应幅值相比,4 号机组改造后脉动压力作用下三层楼板总体振动响应幅值降幅超过50%。改造前后机组100%出力工况下的三层楼板结构振动响应大于75%出力工况。

图2 机组改造后发电机层楼板振动响应最大值相对改造前降幅(75%出力)Figure 2 Decreasing amplitude of the max.vibration response on generator floor after and before runner renovation(75% output)
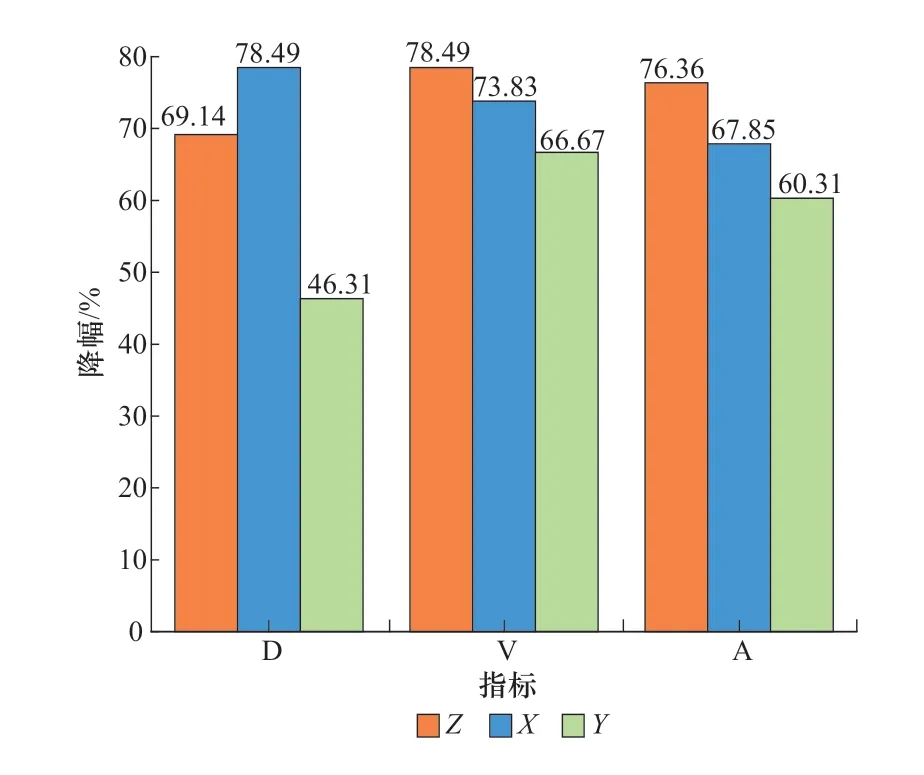
图3 机组改造后发电机层楼板振动响应最大值相对改造前降幅(100%出力)Figure 3 Decreasing amplitude of the max.vibration response on generator floor after and before runner renovation(100% output)
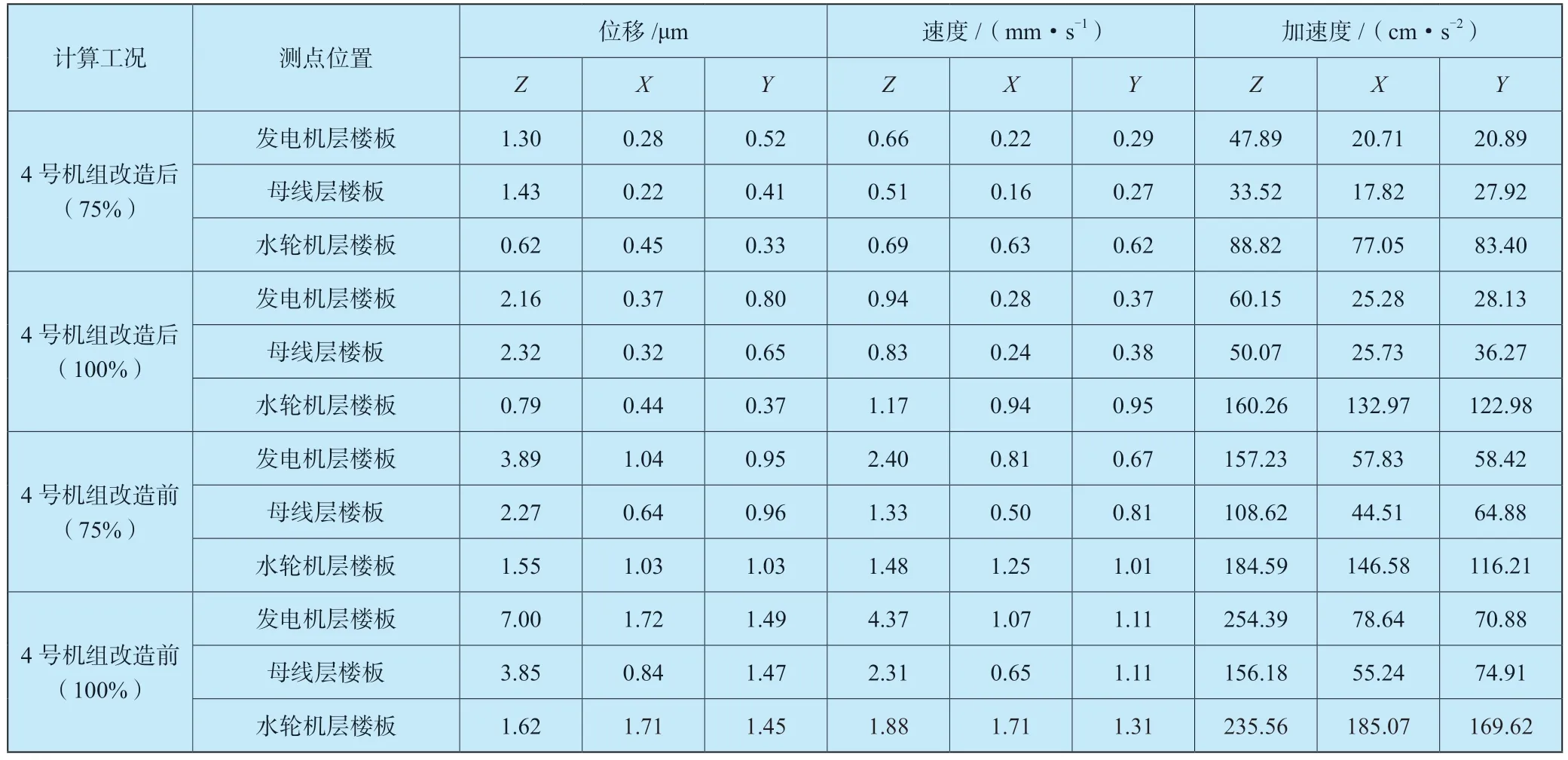
表4 三层楼板振动响应最大值统计Table 4 Maximum of vibration response on three floors
2.3 机墩振动响应计算分析
三层机墩振动响应最大值统计于表5。从数据中可以看出:各工况下,三层机墩竖向(Z向)振动响应总体比水平向振动响应大。在4 号机组改造后水力振源作用下,三层机墩的Z向最大位移为1.02μm,水平最大位移为0.59μm。相同出力工况下,与4 号机组改造前脉动压力作用下三层机墩总体振动响应幅值相比,机组改造后脉动压力作用下三层机墩总体振动响应幅值降幅超过50%。4 号机组改造前后100% 出力工况下的三层机墩振动响应大于75% 出力工况。

表5 三层机墩振动响应最大值统计Table 5 Maximum of vibration response of generator piers on three floors
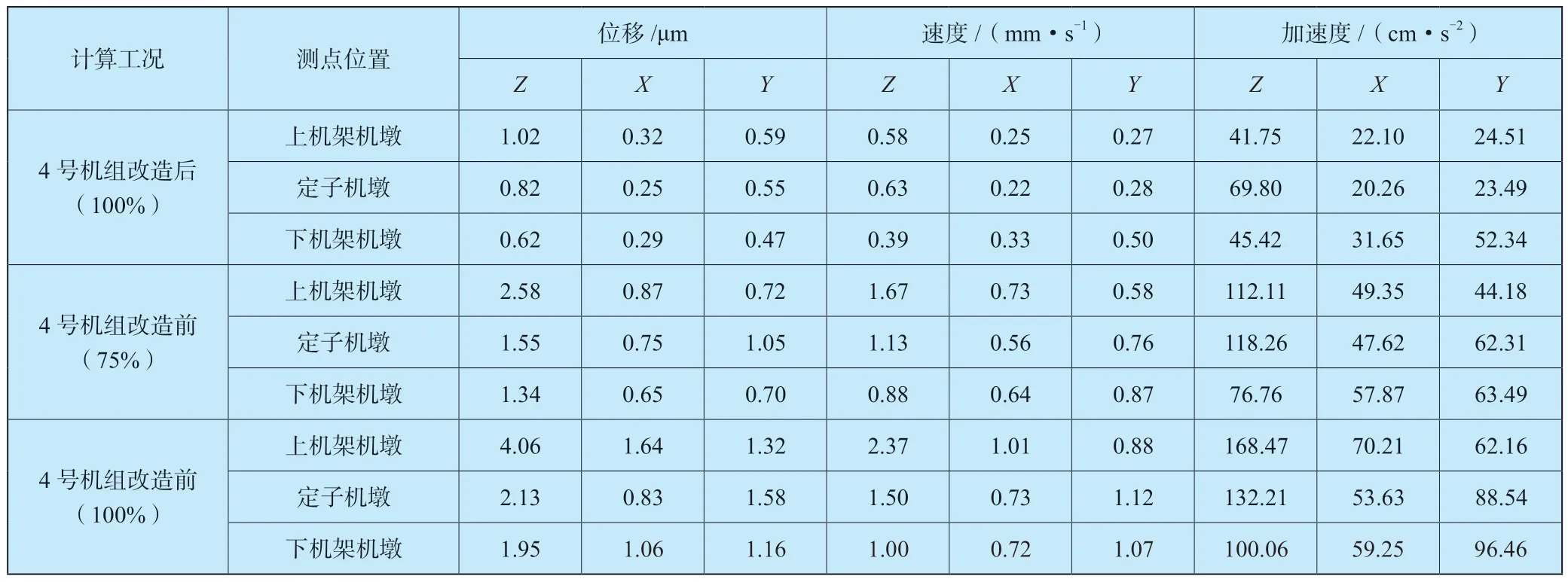
续表
2.4 立柱振动响应计算分析
本次振动响应计算分析选取了6 个立柱,编号分别为P_1 ~P_6;6 个立柱的振动响应的最大值统计于表6,不同工况个别立柱的振动响应变化见图4 ~图5。通过对数据的分析,结果表明:4 号机组改造后运行时,6 个立柱的最大水平位移不到1.0μm,根据日本学者畑中元弘归纳的不同研究者提出的建筑物振动允许界限[2],强度特别好的建筑物振动位移允许值为135 ,立柱的最大水平位移远小于该值,因此不会影响立柱结构安全。相同出力工况下,与4 号机组改造前脉动压力作用下6 个立柱总体振动响应幅值相比,改造后脉动压力作用下6 个立柱总体振动响应幅值降幅超过50%。
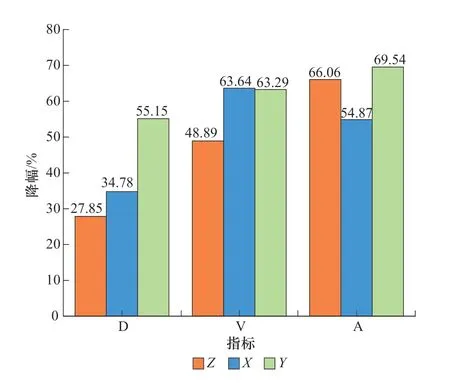
图4 4 号机组改造后运行时立柱P_1 振动响应最大值相对改造前运行时的降幅(75%出力)Figure 4 Decreasing amplitude of the max.vibration response of stand column P_1 after and before runner renovation(75% output)
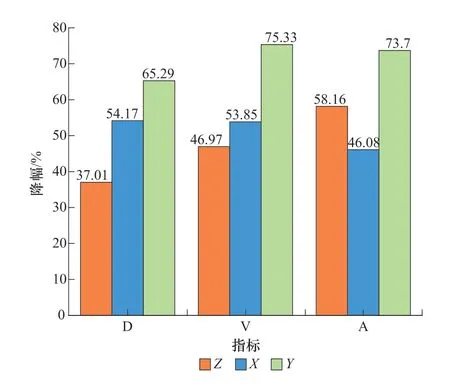
图5 4 号机组改造后运行时立柱P_1 振动响应最大值相对改造前运行时的降幅(100%出力)Figure 5 Decreasing amplitude of the max.vibration response of stand column P_1 after and before runner renovation(100% output)
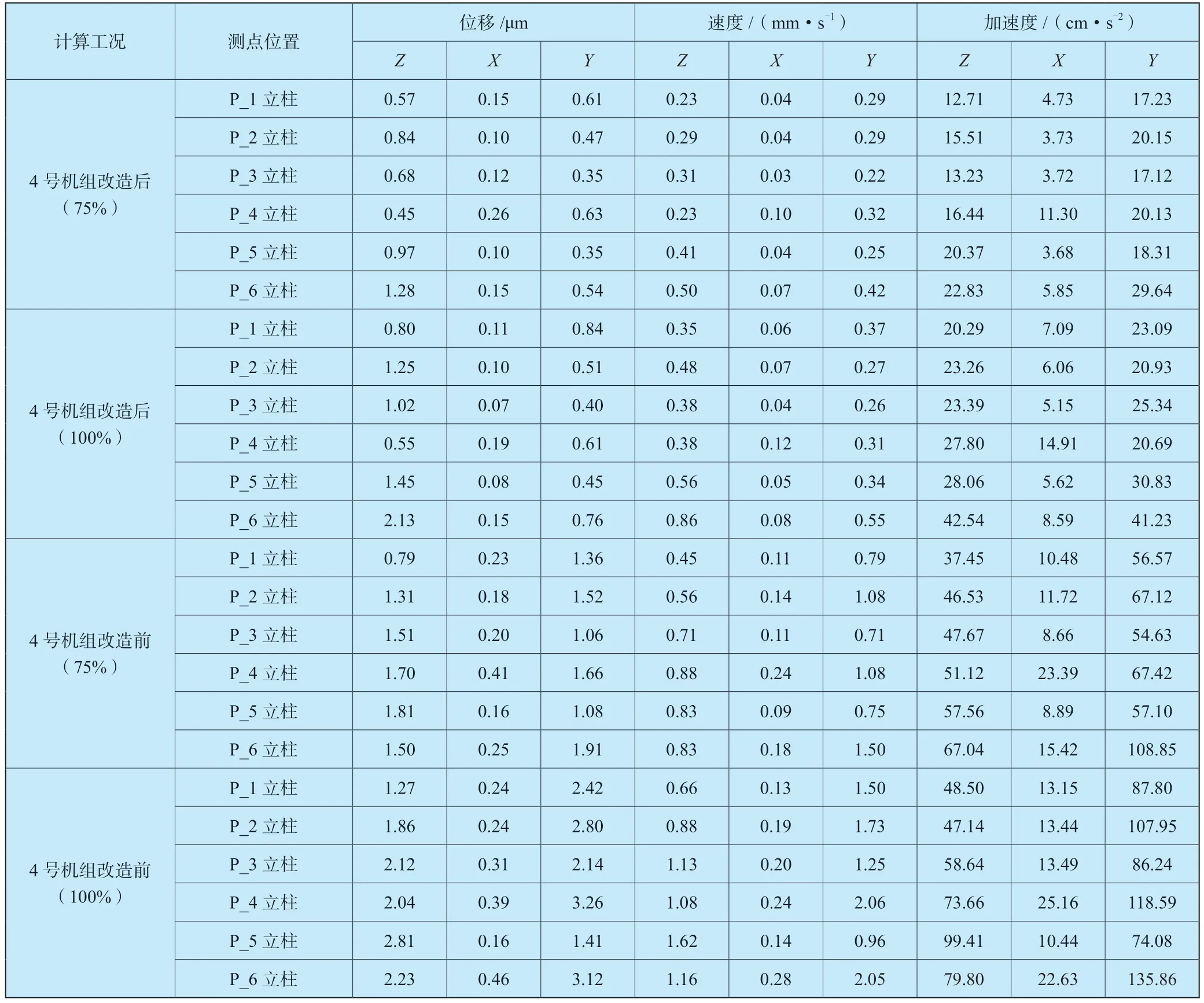
表6 6 个立柱振动响应最大值统计Table 6 Maximum of vibration response of six stand columns
机组调试期间对厂房布置了部分测点进行现场实测,从试验结果来看,除个别测点,计算值与实测值整体来看基本相当,大多数测点计算偏差小于5cm/s2,整体来看,计算模型及边界条件选取准确,计算结果可信,可用于厂房振动安全评价。
3 结论
本文针对黑麋峰抽水蓄能电站4 号机组6+6 长短叶片转轮对厂房振动影响问题,创建了厂房三维有限元模型,采用机组更换转轮前后的脉动压力测试数据,开展了厂房结构振动响应计算分析,对比了不同转轮特性机组对厂房振动的影响,分析统计表明,相同出力工况下,与4 号机组转轮改造前脉动压力作用下厂房结构总体振动响应幅值相比,转轮改造后厂房结构总体振动响应幅值降幅超过50%。4 号机组转轮改造后振动响应显著优于转轮改造前。
通过机组转轮叶片型式改造前后的厂房振动响应分析对比表明,黑麋峰抽水蓄能电站4 号机组转轮叶片型式由9叶片改造成6+6 长短叶片,有效降低了机组运行引发的厂房振动。
——“AABC”和“无X无X”式词语

