勘测自推式钻地机器人螺旋钻进轴特性分析*

张 晋,伍 强,周 鹏,董绍江,朱孙科

(1.重庆市勘测院,重庆 401120; 2.重庆市轨道交通(集团)有限公司,重庆 401120; 3.重庆交通大学 机电与车辆工程学院,重庆 400074)

0 引 言

钻地机器人是一种能够在多种地下与土壤环境中执行各项困难任务的极限作业机器人。和传统钻进设备相比,钻地机器人具有体积小、机动性强和灵活性高的特点[1]。根据工作环境、土壤状况以及机器人的结构与载荷性能的不同,钻地机器人所能完成的任务也各有不同[2]。目前自推式钻地机器人已在地下勘探、行星土壤取样与探测、地震火灾后的搜救工作、水底打捞辅助等领域得到了广泛应用。

Myrick等[3]在美国航空航天局的支持下发明了一种自推进式深孔钻进机器人,用于太空行星的土壤取样、勘测工作。日本宇宙科学研究所提出了一种用于月球勘测的螺旋式钻进机器人。该机器人通过螺旋叶片的旋切运动将土壤切除并向后输送,同时利用螺旋的向后输土动作产生钻进所需的推进力[4]。日本筑波大学与HDK和UNIVANCE两公司合作,开发了一种小型钻掘机器人“Digbot”,主要用于地质勘测和月球探索[5]。随着我国航空航天实力的快速提升和航天事业的有效开展,国内亦有众多优秀的研究成果。哈尔滨工业大学的Zhang等[6]以尺蠖运动为灵感,设计了一种有线尺蠖钻井机器人。此方案通过在机器人前后端设置旋向不同的螺旋叶片进行钻井和排屑,并通过月球土壤环境的土力学模拟分析,验证了方案的可行性。

笔者针对勘测机器人的发展需求,进行了勘测用自推式钻地机器人的总体设计,并对螺旋钻进轴叶片受力、螺旋钻进轴叶片临界转速等做了研究,采用有限元法分析了螺旋钻进轴力学特性。为勘测自推式钻地机器人设计提供指导。

1 自推式钻进机器人结构与工作原理

自推式钻地机器人主要分为冲击型、蠕动型和螺旋钻进型三种类型。其中,螺旋钻进型钻地机器人依靠螺旋钻具掘削土壤产生的轴向推力实现自身的钻进作业。其上设置多个螺旋轴,可通过螺旋轴的旋转差异产生的不同大小或不同方向的轴向力实现机体的转向,整体结构较为紧凑、工作平稳可靠,多用于陆上、太空土壤的探测取样或工程用孔洞挖掘工作。

自推式钻地机器人的整体结构如图1所示。其工作方式为螺旋钻进,机器人在土壤中的钻进与转向工作主要依靠螺旋钻具对土壤的掘削作业来实现。机体结构主要分为三部分,分别为攻土钻头、螺旋钻具和动力装置,其中螺旋钻具是机器人的核心部件,它是主要工作原件,同时也是构成机器人的主体结构,并连接机器人的各个部件。螺旋钻具的输入端通过联轴器与减速箱相连,从而实现较低转速的掘削旋转运动。

图1 勘测用自推式钻地机器人结构

2 螺旋钻进轴叶片受力分析

由于螺旋钻具的螺旋叶片宽度较窄,螺旋升角变化幅度不大,而且需考虑土壤与孔壁之间的摩擦力,因此取螺旋叶片边缘的土壤微元,采用临界转速经典模型[7]对其进行准静力学受力分析。在临界转速经典模型中,被掘削的土会被视作单独的粒子,其由于受到螺旋叶片的回转运动产生的离心力的作用而与孔壁接触,并受到与孔壁间形成的摩擦驱动力的作用而被排出,与其他被掘削的土无关。根据临界转速经典模型建立如图2所示的力学模型。图2中β为螺旋叶片外缘的螺旋升角;Ψ为土被切削下后的运动轨迹的螺旋上升角,反映了螺旋机构输送土壤的能力;F1为土在受到科氏加速度的影响的情况下与孔壁间形成的摩擦力,其方向与土做旋转运动的方向相反,有一定阻碍土随螺旋叶片一同旋转的功能,是螺旋叶片上的土向上或向后运动的动力;F2为土与螺旋叶片之间的摩擦力;F3是土的重力延叶片螺旋倾角方向的分力,同F2一样起阻碍土向上方或后方运动的作用;N为土壤受到的螺旋叶片提供的支撑力。

图2 螺旋叶片输土模型

由图2可得各参数间关系:

G=mg

(1)

F2=μ1N

(2)

(3)

(4)

式中:m为土粒子的质量,kg;g为重力加速度,kg/s2;μ1为土与螺旋叶片间摩擦系数;μ2是土与土之间摩擦系数;R是螺旋叶片的半径,m;ωa是土粒子绝对角速度,rad/s;ω是螺旋叶片旋转的角速度,rad/s;vr是土粒子相对螺旋叶片的速度,m/s。

土粒子处于受力平衡状态,则其在x与y的方向上的受力平衡,因此:

F2+F3-F1sin(β+Ψ)=0

(5)

N-Gcosβ-F1sin(β+Ψ)=0

(6)

对土粒子的速度进行分解与合成,可得其速度合成图如图3所示。图中va为土粒子绝对速度,ve为土粒子牵连点处的牵连速度。

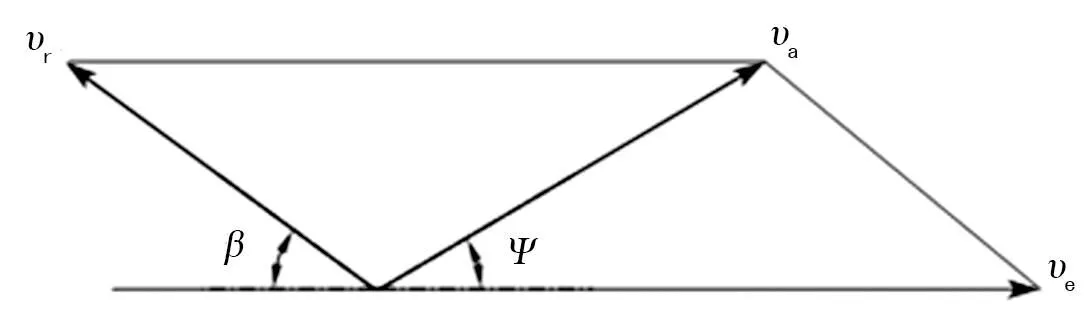
图3 土粒子各项速度关系

ve和vr在垂直于va方向上的分量相等,故:

vesinψ=vrsin (β+Ψ)

(7)

ve=Rω

(8)

由以上公式可得理想状态下螺旋叶片的角速度:

ω=(1+tanΨcosβ)×

(9)

因60ω=2πn,故螺旋叶片转速:

(10)

采用MATLAB进行编程计算,得到螺旋升角、土的运动轨迹上升角与螺旋叶片转速间的关系,如图4所示。

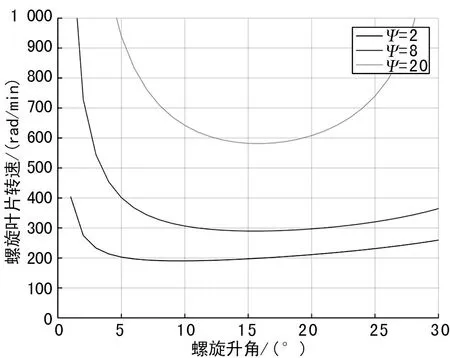
图4 螺旋升角、土粒子运动轨迹上升角和叶片转速关系

由图4可知,若土粒子运动轨迹上升角相同,则外缘螺旋升角存在最优值,此最优值可使钻地机器人在钻进过程中所需的转速最小;而随着土粒子运动轨迹上升角的逐渐增大,钻地机器人钻进时所需的转速就越高,且螺旋叶片外缘螺旋升角的最优值也会明显增大;此外,在外缘螺旋升角确定的情况下,随着土粒子运动上升角的增加,钻地机器人钻进时所需的转速也会随之快速增大。

3 螺旋钻进轴叶片临界转速分析

“临界转速”是指螺旋叶片上被掘削下的土有着相对螺旋叶片发生运动的趋势时的一种临界状态[8]。若螺旋钻具的转速能够大于这一“临界转速”,便可以达到将土向与螺旋钻具钻进相反的方向输送的目的,否则容易出现土在螺隙间卡阻的现象,严重时会发生卡钻现象,造成作业事故。

当螺旋叶片上被掘削下的土处于临界状态时,其处于平衡状态,并没有实际发生与螺旋叶片的相对运动,故此时其处于受力平衡状态。受力情况如图5所示。

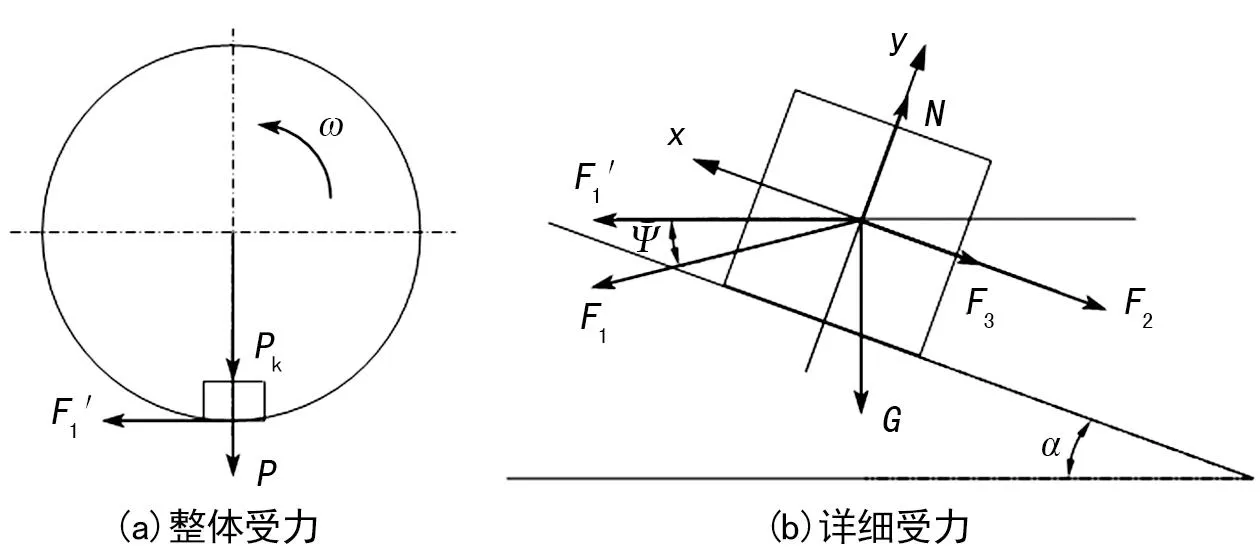
图5 螺旋叶片上土临界转速受力情况

图中P为旋转产生的离心力,Pk为受科氏加速度影响产生的惯性力[9],这一惯性力使得原本呈水平状态的土与所钻孔洞孔壁间的摩擦力F1′向下偏斜角度Ψ,进而产生土运动轨迹的上升角。

土的临界转速用n0(rad/min)表示,由于实际钻进工况下,应保证螺旋钻具钻进的平稳性,因此其转速一般不高,由经验公式得n0表达式:

(11)

(12)

式中:K为土相对螺旋叶片的转速nr与土的临界转速n0的比值,K=nr/n0;α为包含一个螺旋叶片宽度上所有土的运动情况,依经验公式取螺旋叶片位于螺旋钻杆处摩擦角进行计算;v是钻地机器人钻进的速度,m/s。

4 螺旋钻进轴有限元分析

螺旋轴作为自推式钻进钻地机器人最为核心的部件,需完成对土壤的掘削以完成机器人的钻进工作。螺旋轴的两端通过角接触球轴承与底层机架和上层机架配合,以限制其轴向移动。因此,其主要承担掘削土壤时产生的扭矩和钻进时轴体所受轴向力。螺旋轴的材料选用密度小、强度高的铝合金,材料性能如表1所列。

表1 铝合金材料属性

为便于分析,对螺旋轴的钻进情况进行简化后对其进行分析。假设被掘削后的土壤在螺旋叶片上是均匀分布的,轴主要运动形式即竖直钻进运作,因此所受轴向阻力竖直向上,所受扭矩绕轴向在螺旋轴周身与螺旋叶片边缘均匀分布。

为提升分析精度与实际计算效率,对螺旋轴进行网格独立性验证,分别对螺旋轴进行5 mm、2.5 mm和2 mm网格尺寸分析,结果如表2所列。

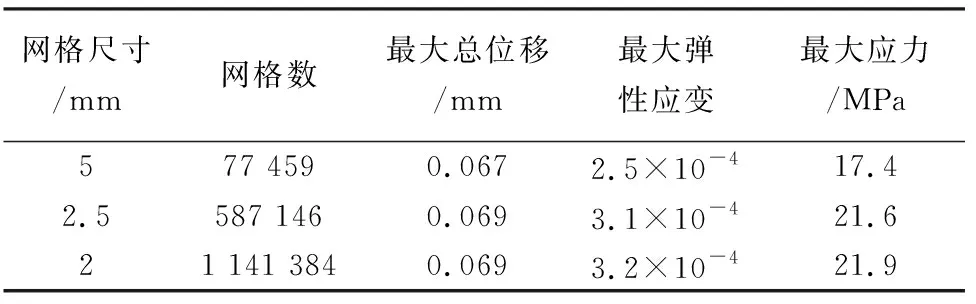
表2 螺旋轴不同网格划分计算结果

由表2对比结果可知,当网格尺寸为5 mm时,所得结果精度较低,而将网格划分至2.5 mm与2 mm后,结果精度有明显提升,且二者分析结果差别不大。因此选择运算效率更高的2.5 mm尺寸的网格对螺旋轴进行划分,网格划分结果如图6所示。

图6 螺旋轴局部网格划分 图7 螺旋轴约束与载荷分布

以轴旋转状态的较大载荷情况为基准进行静应力分析,并在轴顶端键槽处添加固定约束。将轴所受扭矩简化至轴的周身与螺旋叶片的边缘,所添加扭矩近似取较大值M1=3.3 N·m,在螺旋叶片底部添加延轴运动方向反向的轴向力,近似取较大值Faz=353 N。约束与载荷添加结果如图7所示。

螺旋轴位移云图和应力云图如图8、9所示。由图可得,螺旋轴上部位发生的形变极小,最大变形处主要集中在螺旋轴底部首先对土壤进行掘削的部位,其值较小,对螺旋轴的推进运动影响不大。而螺旋轴所受最大应力约为21.6 MPa,主要发生在驱动轴进行旋转运动的键槽和螺旋叶片与轴的焊接处,远小于材料许用应力,因此在正常工作中不会出现故障失效问题,螺旋轴的设计合理。

图8 螺旋轴位移云图 图9 螺旋轴应力云图

图11 成品滑轮

5 结 语

文章设计了一款勘测用自推式钻地机器人,研究了该机器人的螺旋钻进轴叶片受力和螺旋钻进轴叶片临界转速。采用MATLAB编程计算了螺旋升角、土的运动轨迹上升角与螺旋叶片转速间的关系,获得了外缘螺旋升角的最优值。对螺旋钻进轴进行了有限元力学性能分析,通过网格依赖性分析获得了最佳的网格尺寸,应力和位移结果表明所示的螺旋钻进轴能够满足设计要求。