阶梯式预测控制在SCR脱硝控制中的应用

李昱

(杭州和利时自动化有限公司, 浙江, 杭州 310018)

0 引言

煤燃烧过程中氮氧化物(NOx)的排放已成为环境污染的一个重要问题,并对空气质量产生了重大影响[1]。快速有效的减排已经成为燃煤电厂最重要的问题之一。目前,选择性催化还原法(SCR)因其脱硝效率高、成本低、技术成熟而受到广泛关注和应用[2]。同时,SCR系统的建模和控制优化也受到了广泛的关注。

在火电厂的SCR脱硝系统中,通常采用PID控制。然而,由于SCR脱硝系统具有大惯性、时滞、多变量、时变等特点,常规的PID控制难以满足控制质量要求,一旦控制不佳,氨水喷洒过量时,氨气会逸出,污染环境,并增加成本。因此,对于火力发电厂的可SCR控制系统,迫切需要提出新的智能控制策略,以降低成本,同时最大限度地减少氮氧化物的排放。在脱硝系统的建模方面:文献[3]通过深度学习网络建立了SCR系统出口NOx浓度的预测模型;文献[4]基于SCR系统变量间的相关性建立了自适应惰性学习算法;文献[5]基于时间差分法和最小二乘支持向量机建立了SCR脱硝系统的动态模型。在控制器设计方面:文献[6]利用BP神经网络建立了NOx浓度控制模型,结合遗传算法(GA)和模型预测控制,实现了出口NOx浓度的神经网络模型预测控制;文献[7]提出了一种使用在线最小二乘支持向量机的自适应抗干扰MPC,并使用卡尔曼滤波器来评估过程模型中不可测的干扰;文献[8]利用神经网络反馈线性化算法控制喷氨阀,对NOx浓度进行优化控制,使其达到排放标准。

上述无论是SCR的系统建模还是控制优化,都较少考虑算法本身的实际应用效率问题,本文针对某电厂高温高尘布置方式的SCR脱销系统建立了两入一出的传递函数模型。考虑到实际电厂对智能算法计算效率的要求,通过阶梯式策略对动态矩阵预测控制(DMC)算法进行了改进,改进后的阶梯式DMC(SDMC)避免了大型矩阵求逆计算,大大简化了求解过程。通过与PID控制器的对比仿真可知,本文设计的SDMC非常适用于实际热工过程控制。

1 SCR脱硝系统模型

目前,从烟道的安装位置划分,SCR脱硝系统的布置可分为高温高尘、高温低尘以及低温低尘。综合考虑3种方法的优缺点,处于省煤器下游、空气预热器和电除尘器上游的高温高尘布置最为经济有效,已被国内大多数电厂采用[9]。

采用这种布置,锅炉产生的烟气在通过省煤器后温度更高,无须额外的预热装置,与喷氨格栅喷射的氨/空气混合气体一同在脱硝反应器中进行反应,其涉及的主要化学反应[10]为

4NO+4NH3+O2→4N2+6H2O

2NO2+4NH3+O2→3N2+6H2O

(1)

某电厂1000 MW机组SCR脱硝系统采用高温高尘布置方式,系统的控制量为脱硝阀门开度,被控量是出口NOx浓度,入口NOx浓度则为可测量的扰动。为避免电厂实际运行环境中的有色噪声对SCR脱硝系统对象模型参数估计造成影响,在MATLAB中通过辅助变量最小二乘法进行SCR对象模型辨识的算法实现[11],得到传递函数模型如下:

(2)

式(2)中,Y(s)为出口NOx浓度,U(s)为SCR脱硝阀门开度,D(s)为入口NOx浓度。

2 阶梯式动态矩阵控制(SDMC)

2.1 预测模型

本文首先获得式(2)所示SCR被控对象的单位阶跃响应作为DMC的预测模型。假设系数ai=a(iT),i=1,2,…为对象单位阶跃的输出采样值,其中T表示采样周期。在阶跃响应趋于稳定时截断模型,即可求得限定时间范围内的阶跃响应序列[12],即

a=[a1,a2,…,aN]T

(3)

式(3)中,N为建模时域。

若k时刻在系统的输入端引入单位控制增量Δu(k),那么k+i时刻的预测值如下:

(4)

(5)

式(5)中,M为控制时域。

将式(5)改写成向量形式:

(6)

式(6)中,

(7)

(8)

(9)

Δu(k)=[Δu(k),Δu(k+1),…,Δu(k+M-1)]T

(10)

式(7)～式(10)中,P为预测时域。

2.2 滚动优化

DMC算法的优化采用滚动优化计算方式来实现,通常采用式(11)所述的二次型优化指标函数:

(11)

式(11)中,wP(k)为输出期望值,Q为误差权矩阵,R为控制权矩阵。

wP(k)=[w(k+1),…,w(k+P)]T

(12)

Q=diag(q1,…,qP)

(13)

Ρ=diag(r1,…,rM)

(14)

(15)

式(15)中,ΔuM(k)为k时刻最优的控制增量向量。在实际控制过程中,仅执行当前控制律,即u(k)=Δu(k)+u(k-1),而在下一采样周期,重新进行上述优化计算。

2.3 阶梯式策略

通过引入阶梯式控制的思想,控制变量的未来增量可以被明确规划为

Δu(k)=δ,Δu(k+1)=βΔu(k+i-1)=βiδ,1≤i≤M-1

(16)

因此,未来时刻的控制序列变为

ΔU=(Δu(k) Δu(k+1) … Δu(k+M-1))

=(δβδ…βM-1δ)=(1β…βM-1)δ

(17)

从式(17)可知,控制量u的形式呈现阶梯状,变化较为稳定均衡,且控制率求解时不需进行矩阵求逆,使计算量得到较大简化,稳定性也得到提高[11]。

(18)

式(18)中,G为P×1的列向量。

预测模型可表示为

(19)

式(11)所示的性能指标函数可表示为

(20)

式(20)中,λ为控制矩阵系数,β为阶梯因子。

极小化目标函数(20),令∂J/∂δ=0,得到控制率为

(21)

在实际控制时只实施当前控制量u(k)=u(k-1)+δ。到下一时刻,根据最新得到的反馈信息,可重新求得预测值并进行优化计算。根据式(21)可以发现,求解的控制律不再需要矩阵求逆,且从矩阵相乘转变为向量相乘,使计算变得更加简便。

2.4 反馈校正

由于电厂运行过程中会产生各种噪声及干扰,导致SDMC控制器的预测值与实际输出会出现发散偏离。为解决这一影响,需对预测模型进行反馈校正。

当k时刻的控制增量δ作用于对象时,根据式(6),可计算得到未来的输出预测值:

(22)

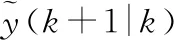
(23)

上述误差无因果关系,从而使用启发式方法实现预测误差,如式(24):

(24)

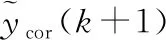
(25)

3 基于SDMC的脱硝控制仿真

本文基于MATLAB 2020b Simulink工具搭建了SCR-SDMC控制仿真系统如图1所示。

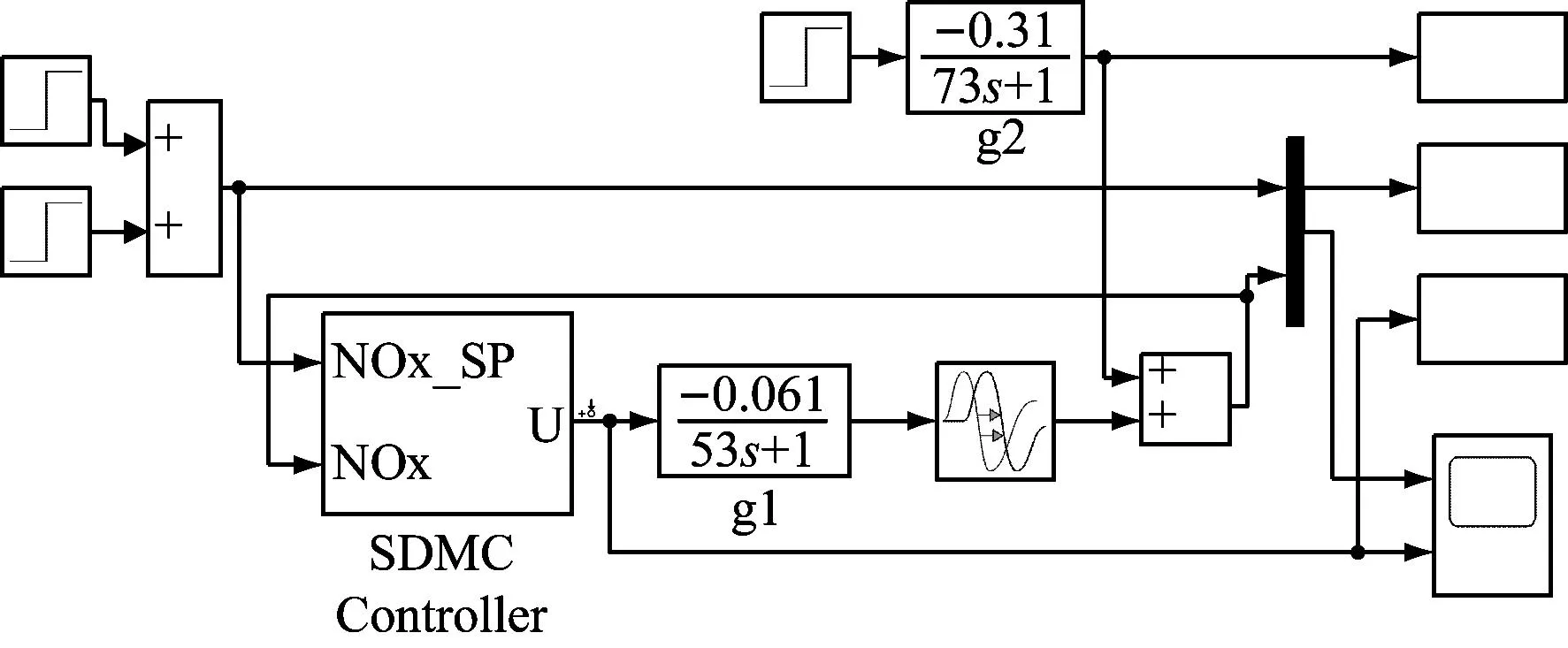
图1 SCR-SDMC控制仿真图

为了验证SDMC在SCR对象上的控制效果,本文进行了设定值扰动试验、入口NOx扰动量扰动试验以及模型失配等试验,并与经MATLAB自整定工具整定后的PID控制器进行了对比。SDMC控制器参数为N=1000,P=250,M=20,β=0.1,λ=1,采样周期T=1 s。PID参数为P=-5.8,I=-0.06。

3.1 设定值扰动仿真

待整个控制系统稳定运行后,于t=100将出口NOx浓度从30 mg/m3阶跃为35 mg/m3,并继续运行1100 s,响应曲线如图2所示。

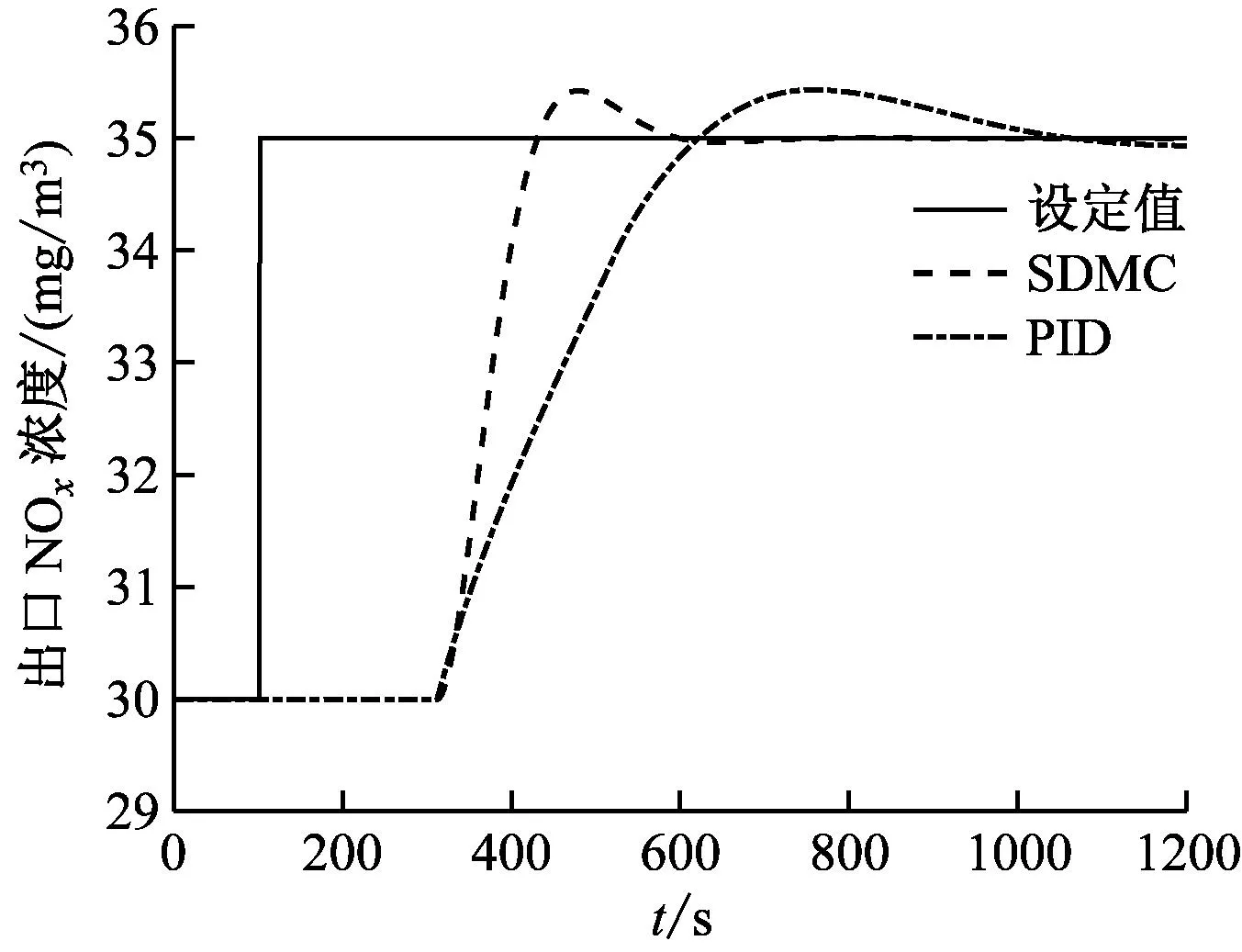
图2 设定值扰动下的响应曲线

从图2可以看出,在SDMC和经优化整定后的PID控制作用下,SCR系统超调均在5%以内,但SDMC调节要比PID快240 s,SDMC具有良好的控制效果。

3.2 扰动量扰动仿真

(1) 阶跃扰动仿真

在t=0时,将入口NOx浓度在原稳定状态下阶跃增加20 mg/m3,仿真共运行1500 s,SDMC与PID控制器控制效果如图3所示。

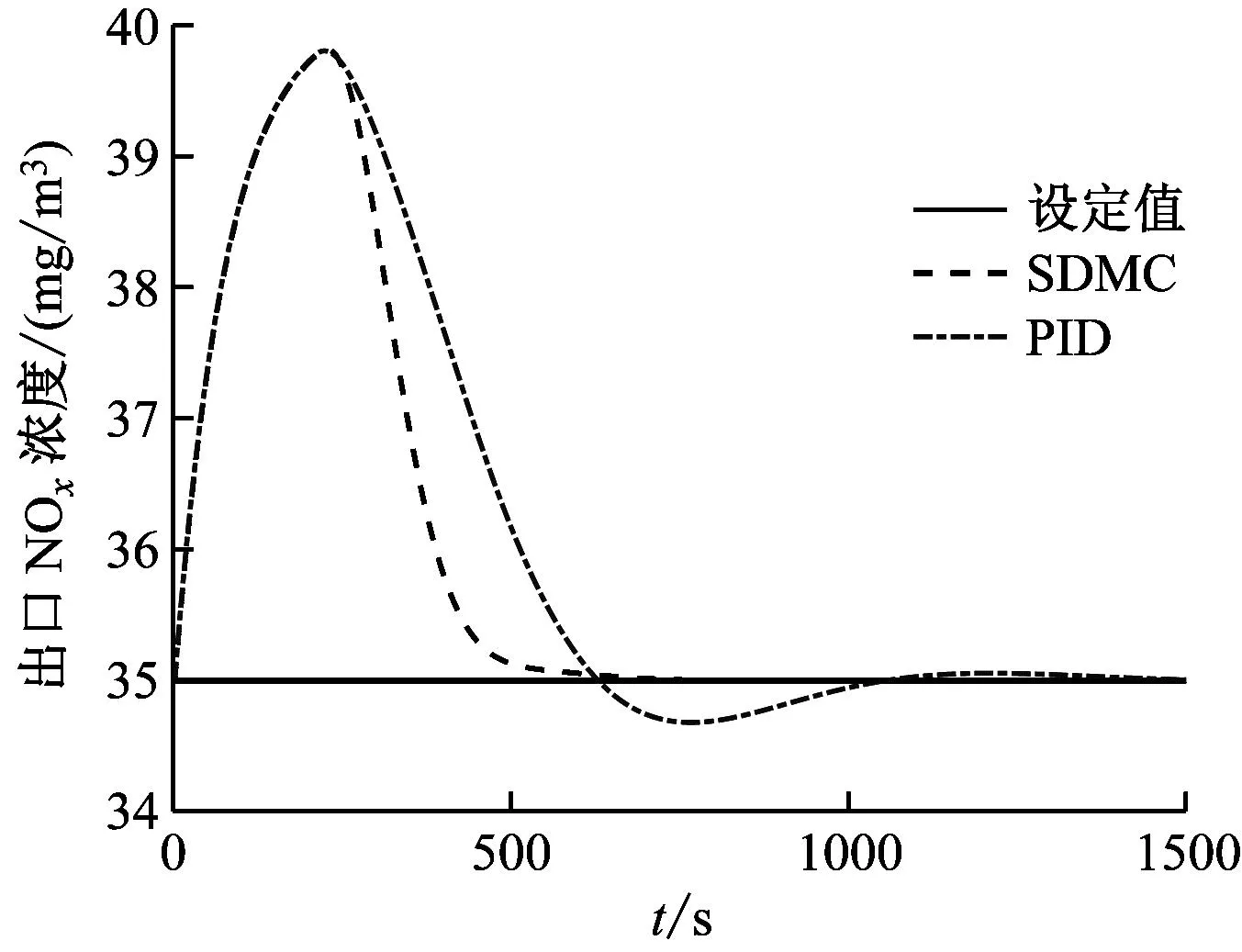
图3 输入阶跃扰动下的响应曲线

由于入口NOx浓度是一个扰动量,所以当NOx浓度阶跃增加时,一开始控制量还未起作用,出口NOx浓度随入口NOx浓度的突增而不断上升,在度过被控对象迟延时间,即210 s后,SDMC立即开始控制作用,出口NOx浓度逐渐下降,回到原稳定状态。从图3可知,SDMC在对象迟延介绍后,能快速抑制扰动,没有任何超调,调节速度也比PID更强。

(2) 实际输入扰动仿真

为了充分验证算法在工程实际中应用的可行性,本文通过模拟电厂入口NOx浓度实际情况,即入口NOx随着时间演进,其扰动值是一个在幅度和周期上均变化的量。本文将幅度在25 mg/m3附近波动的一组入口NOx浓度值在t=0时注入,仿真运行2000 s,SDMC与PID控制器控制效果如图4所示。

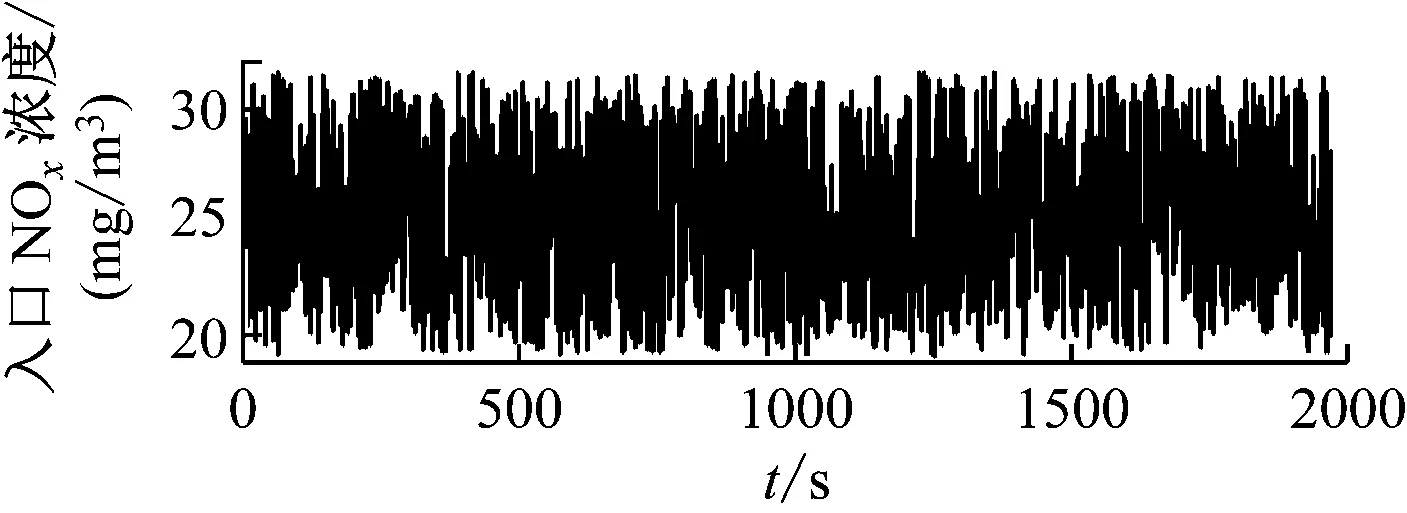
(a) 入口NOx浓度扰动

从图4可以看出,在入口NOx浓度连续波动的情况下,SDMC与PID仍能最终恢复稳定,但SDMC恢复稳定的时间比PID快,而且与PID相比,在SDMC控制下,SCR系统不需要经过多次上下波动便可直接稳定。

3.3 模型失配仿真

为了进一步验证SDMC的控制性能和鲁棒性,通过对SCR对象进行失配处理,即将SCR传递函数模型增益K、迟延时间tao和惯性时间T异化处理进行验证。失配处理后的不可测控制通道模型如下:

(26)

同样,系统稳定运行后,在t=100时,将出口NOx浓度设定值由30 mg/m3阶跃为35 mg/m3,并继续运行1100 s,响应曲线如图5所示。

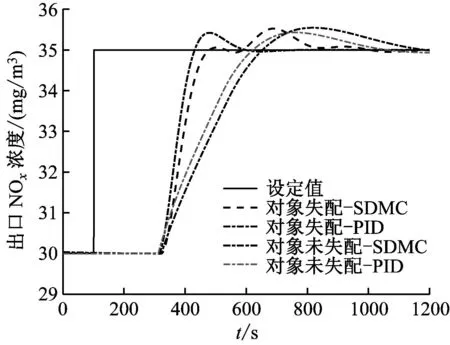
图5 模型失配情况下SDMC参数优化前的控制响应曲线

从图5可知,在模型失配情况下,若SDMC超参数不做任何修改,会有小幅度波动,但仍比PID更快稳定下来。在模型预测步骤中建模向量保持不变的情况下,通过调节相关超参数,可进一步改善模型失配情况下的调节效果,如图6所示,经SDMC超参数调节后,波动明显减小,从而进一步验证了SDMC的鲁棒性。

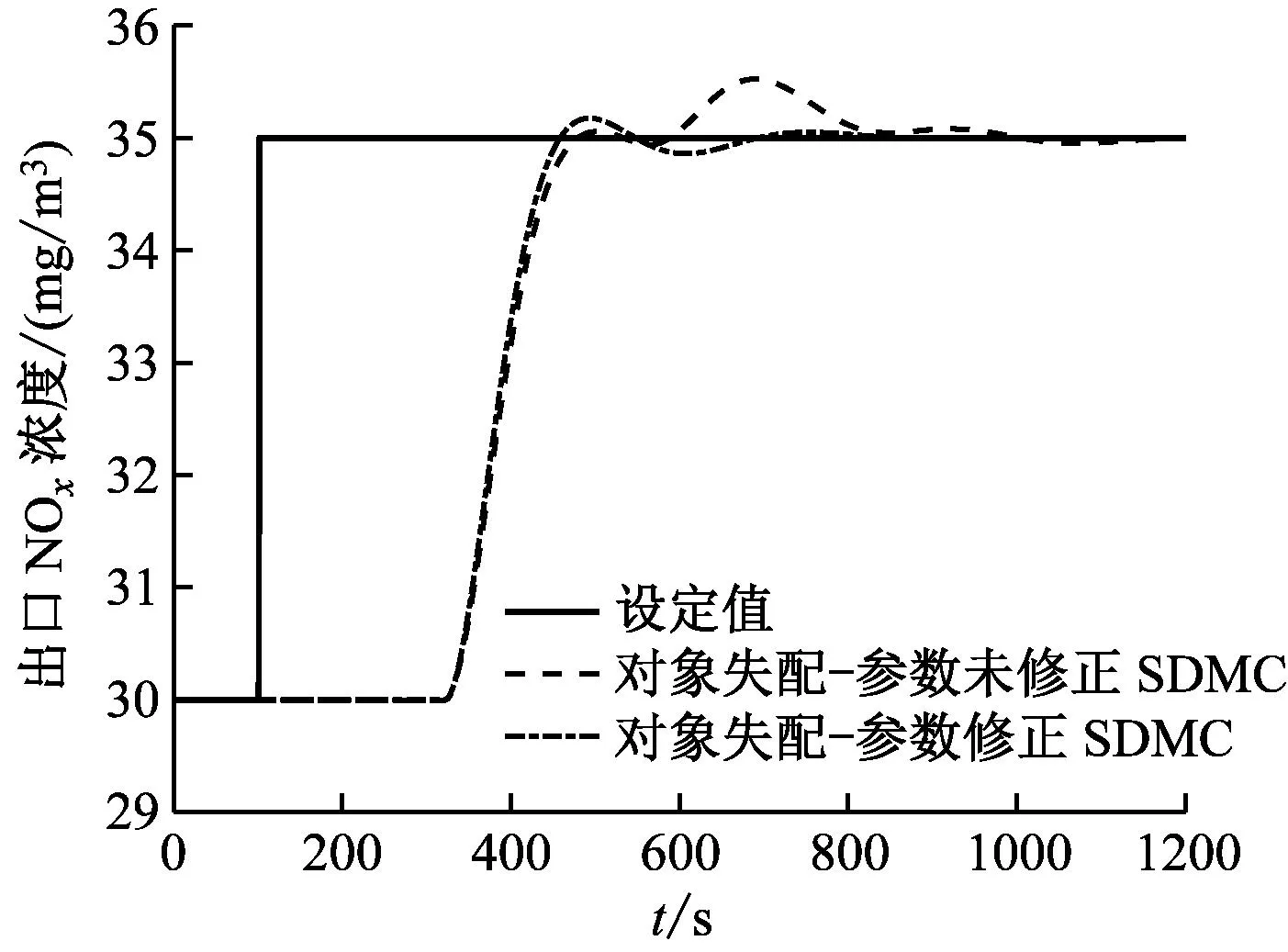
图6 模型失配情况下SDMC参数优化后的控制响应曲线

3.4 运行时间对比仿真

为了验证本文方法的高效性,对SDMC和DMC 2种算法在每个在线滚动优化计算的周期内进行耗时统计,2种算法均取实际输入扰动仿真下运行10次的平均耗时,对比曲线如图7所示。

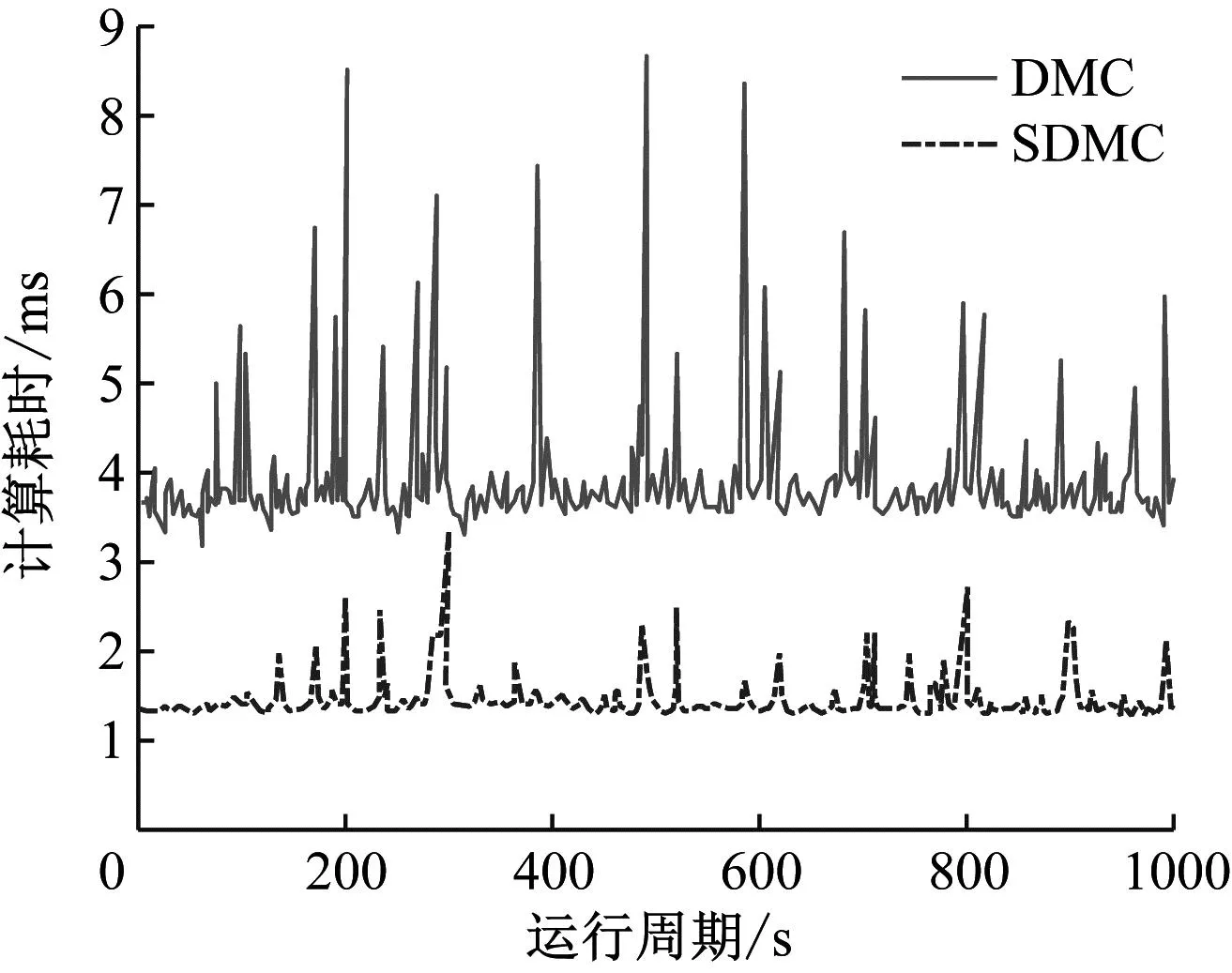
图7 算法耗时计算对比

从图7可知,SDMC在每个优化计算周期内的耗时均比DMC算法短,这种情况会随着控制对象复杂性和耦合性的增强而越发突出。这也进一步验证了本文方法更适用于电厂工程实际应用。

4 总结

本文在分析高温高尘布置SCR脱硝系统对象基础上,基于改进最小二乘法辨识得到了控制量和可测扰动量的传递函数模型。基于阶梯式策略对动态矩阵算法进行了改进,避免了矩阵求逆计算,并将矩阵求解化简为向量求解,大大减小了计算量。通过与PID控制器对比仿真可知,SDMC对NOx出口浓度变化具有更好地响应特性,能更快地克服输入NOx浓度的扰动。在模型失配情况下,只有小幅度的波动,通过适当超参数调优,能很好地恢复控制性能,具有较强的鲁棒性。最后,通过算法耗时对比,可知本文算法效率更高,更适用于作为电厂复杂热工控制对象的先进控制器。