并联式混合动力发动机神经网络法转矩预测与闭环控制

楼狄明， 唐远贽， 房 亮， 施雅风， 张允华， 仇 杰， 杨 芾

（1.同济大学 汽车学院， 上海 201804；2.上汽集团 乘用车技术中心， 上海 201804）

混合动力汽车相比内燃机车和纯电动车具有显著的油耗低、工作效率高、续航里程可靠的特点，在未来的几十年中将依旧是新能源汽车的主流之一［1］。其中，并联式混合动力汽车架构更加接近内燃机汽车，包含发动机与电机2个动力输出源。其工作模式极具多样性，是近年来企业及研究机构的研发主流［2-3］。

并联式混合动力汽车的动力扭矩输出依赖于发动机与电机之间的扭矩配合，相比于转矩变化时间常数在毫秒级的电机，发动机的瞬态进气量、空燃比波动会导致发动机不稳定燃烧，从而导致瞬态转矩较大波动，再加上各缸供气的不均匀性、废气再循环（exhaust gas recycling， EGR）率等影响，难以实现对发动机转矩的精准控制［4］。现有的量产发动机未配备转矩传感器，在传统发动机ECU（electrical control unit）中仅设有发动机输出转矩预测模块。因此，在混合动力汽车运行过程中，尤其是瞬态变化的过程中，较为准确的发动机的转矩预测对并联式混合动力汽车极其重要［5-6］。

查表法是工业界获得实际运行中发动机转矩的常用方法，所建立的查表脉谱（MAP）一般通过台架试验得到，建立起发动机转矩和转速、进气量、进气压力之间的关系。使用时根据发动机在线测得的参数进行插值查表，得到发动机转矩预测值，其缺点是瞬态过程的预测精度低［7］，且一旦涉及多参数，MAP的维度会激增，从而大幅增加标定工作量及存储运算量。

模 型 预 测 控 制 法（model prediction control，MPC）也是转矩预测研究的热门方法［8-9］，使用发动机可获取信息，例如利用爆震传感器等信息，通过对缸内燃烧、传热进行建模，从而对缸压等信息进行预测，进一步完成转矩预测［8，10-12］。该类方法近年来基本集中在简化模型及优化预测精准度方面，如Park等［13］提出了一种仅使用节气门信息的端口空气质量流量的估计方法，替代了以前研究中使用通过节气门进入进气歧管的空气质量流量信息（称为节气门空气质量流量）和进气歧管中的空气压力信息来估计端口空气质量流量。此外，在开环MPC 的基础上，可以添加部分闭环反馈信息从而对预测信号进行进一步的处理。Kao 等［14］、Chauvin 等［15］对发动机转速信号进行测量和处理，利用时变卡尔曼滤波器来预测瞬态转矩。Lee 等［16］提出了2 种转矩预测方法，其核心都是基于发动机转速瞬时波动，即“随机解析法”和“频域解析法”，建立发动机转矩与曲轴转角、角速度和角加速度的函数关系，进而预测转矩。

神经网络（artificial neural network， ANN）算法是近几年来研究发动机相关问题的热门方法。由于ANN 方法是建立在搭建且训练完成的神经网络模型上，因此也作为MPC 方法的一种，可以针对发动机的特性及燃烧性能进行相应的优化设计［17-18］。在转矩预测领域ANN方法也同样受到了关注，相比于传统的物理化学类模型，ANN模型的变量更加多元化且输入输出几乎不受相关性的要求限制，但是关于ANN 转矩预测的研究基本集中在算法结构优化和误差优化层面［19-20］，少有涉及到多种转矩预测模式与ANN 方法的优劣对比。与众多模型控制方法类似，基于模型的瞬时转矩预测为了保障其准确性，一般都需要建立足够可靠的实时发动机闭环反馈，根据发动机可提供的实际信息进行转矩预测修正。

针对实时转矩预测的准确性及转矩预测修正方式，童毅博士［4］在国内首次提出“动态协调控制”的概念，针对并联式混合动力模式切换的瞬态过程，提出“发动机转矩开环控制+发动机转矩在线预测+电机转矩闭环补偿”的控制策略。合理的转矩预测方式配合动态协同控制，可以实现利用发动机前馈预测模型及当前状态信息的反馈控制方式对预测得到的转矩进行实时修正，从而进一步实现更精确的转矩预测及多动力源的转矩动态协调控制［21-23］。

目前将神经网络直接用于预测发动机转矩并进行动态协调修正的研究较少，常规的修正算法均可以在转矩预测及发动机动态协调控制的基础上继续实现，而本文主要聚焦于神经网络与MAP法在闭环控制中对稳态及变化的发动机转矩预测精准程度对比。利用Simulink及GT-Suite软件搭建联合仿真模型，建立基于发动机转速、进气量/增压压力等参数的转矩预测ANN 神经网络模型，验证对比多种稳态、瞬态工况下MAP法预测的转矩与发动机实际转矩误差。在实际应用过程中，随着发动机参数维度的增加，ANN法将相比于MAP法更有优势，如果简单参数下的ANN 预测比MAP 法更精准，这将对发动机（尤其是混合动力发动机）转矩预测开发具有较大的指导意义和参考价值。

1 建模方法与设置

1.1 GT-Suite和Simulink联合仿真模型

表1为联合仿真模拟的混合动力发动机相关基本性能参数，其中包括进气门开启（intake valve opening, IVO）以及排气门关闭（exhaust valve closing, EVC）曲轴转角可调节范围。

表1 发动机相关参数Tab.1 Engine parameters

基于GT-Suite及Simulink软件的交互模型进行发动机时序性联合仿真，具体原理如图1 所示。Simulink 作为控制型号的发出端，在模型中发挥发动机上混合动力控制单元（hybrid control unit，HCU）的功能，而GT-Suite 模型用来模拟真实发动机的运行情况，并为控制端（simulink）提供时序性的发动机状态参数，且这些参数均为发动机实际运行下的可获取参数。

图1 联合仿真原理模型示意Fig.1 Schematic diagram of joint simulation model

搭建的GT-Suite 发动机模型需要根据发动机台架的试验数据进行标定，其标定的万有工况分布如图2所示。

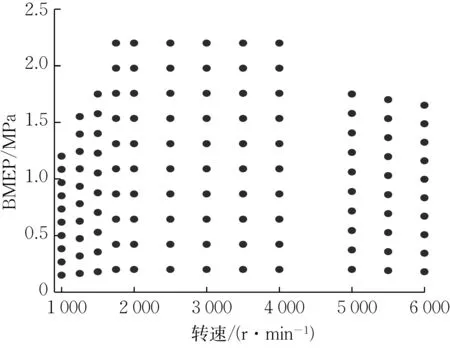
图2 万有工况标定Fig.2 Calibration of working conditions

Simulink模型作为GT的控制端，信号交互如图3所示，以状态输入量发动机转速为固定值，控制信号分别有：节气门开度、增压压力、进气门正时（IVO信号）、排气门正时（EVC信号）、空燃比；发动机反馈状态信号有：发动机转速、进气质量流量、进气温度、进气压力、空燃比、点火提前角、有效转矩、IMEP平均指示压力、燃油循环喷射量、旁通阀开度。同理在GT-Power中也将各控制信号从交互模块连接至执行器、各状态反馈信号从传感器连接至交互模块，如图4所示。

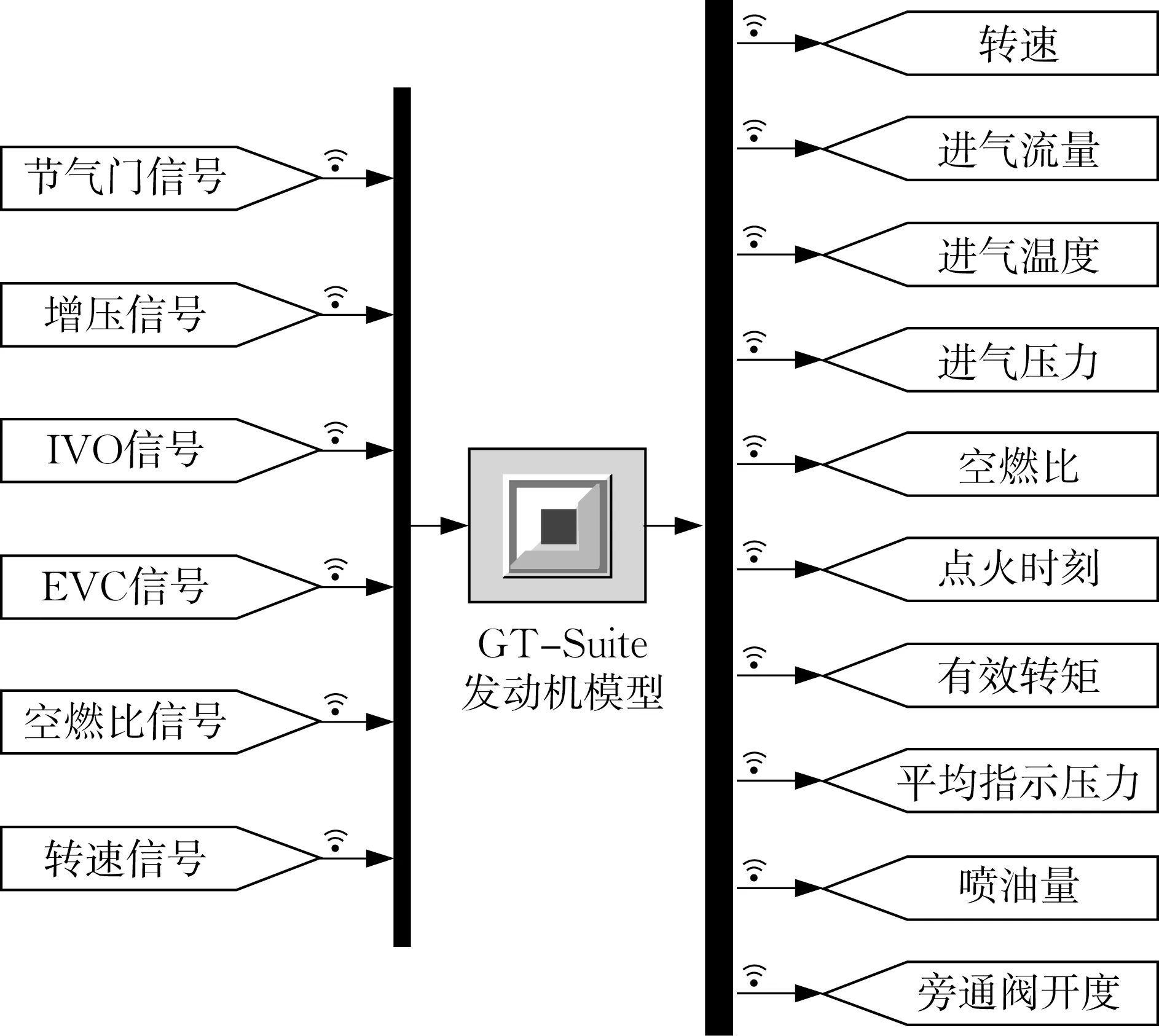
图3 GT & Simulink联合仿真信号交互关系Fig.3 Signal interaction of joint simulation in GT&Simulink

图4 GT-Suite联合仿真模型Fig.4 GT-Suite joint simulation model

1.2 转矩预测方法

转矩预测同时使用MAP 法和ANN 法，这2 种方法都利用进气量和发动机转速这2个变量作为输入参数，比较两者在发动机稳态及瞬态工况下转矩预测及闭环修正控制的准确性。

MAP法是目前发动机上常用的方法，一般是通过台架标定得到的MAP，在实际瞬态工况下进行插值等方式得到相应的转矩，图5是通过GT的万有工况标定得到的进气量、发动机转速与IMEP 关系的MAP图，通过IMEP可以直接计算得到指示转矩。

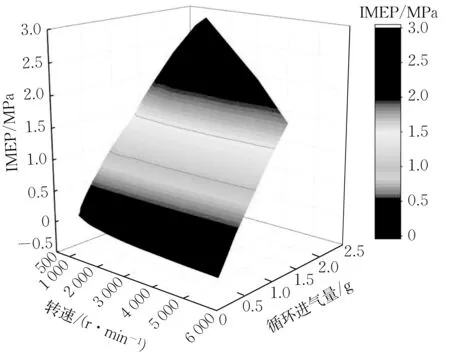
图5 IMEP预测MAP图Fig.5 MAP of IMEP estimation

使用MATLAB 软件中的Neural Fitting 工具箱对神经网络进行构建与训练（见图6）。创建了2 层前馈神经网络，其中一层为隐藏层，神经元函数为Sigmoid，另一层为输出层，神经元为线性函数。采用了Levenberg-Marquardt 的误差反向传播（error back propagation， BP）的训练算法对网络进行训练。对发动机全工况范围内总计840例试验数据进行随机分类，其中80%用于训练网络，10%用于验证网络，最后10%用于测试网络精度。通过调整隐藏层神经元节点数来获得最优的预测效果。

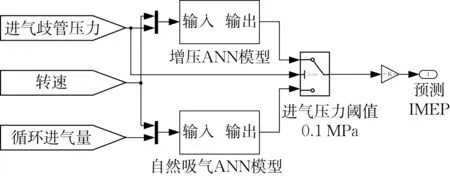
图6 IMEP预测ANN模型Fig.6 ANN model of IMEP estimation

经测试最终在隐藏层节点数为15 时得到神经网络的最优预测效果。由于输入参数量总体较少，总体回归系数如图7所示为0.999 93，表明具有较高的预测精度。

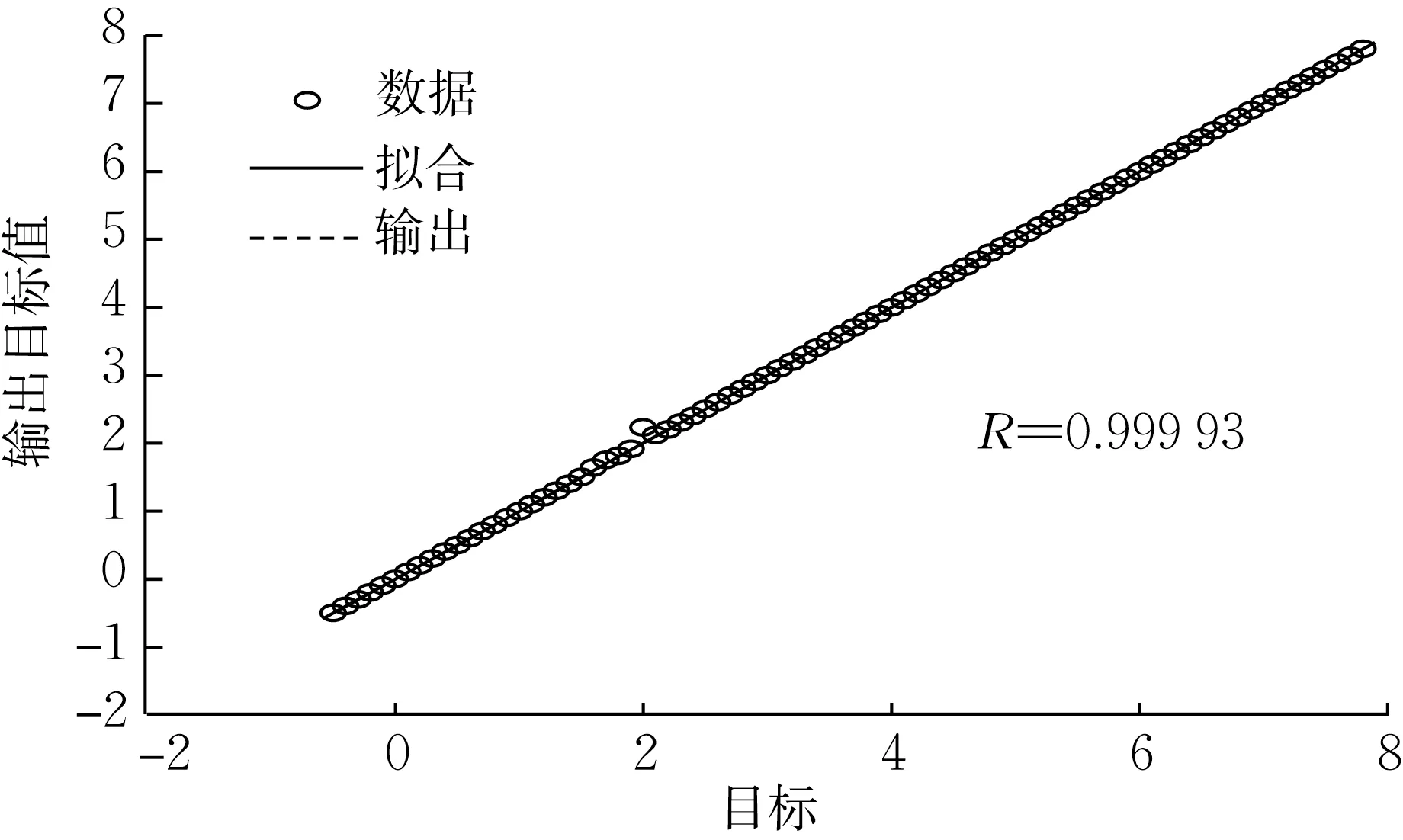
图7 神经网络数据回归分析Fig.7 Data regression analysis of ANN

考虑空燃比对转矩的影响，2种转矩预测算法均需再引入空燃比的修正，得到平均指示压力IMEP的预测值，通过换算得到指示转矩的大小。空燃比修正因子是基于2 000r·min-1、节气门全开、旁通阀全开的工况，通过调节空燃比得到相应的指示转矩，以当量燃烧时的转矩为基准，其他空燃比下的转矩除以当量燃烧的转矩得到空燃比修正因子（φλ），如式（1）所示：

式中：λ为过量空气系数；Tλ=i为任意空燃比下发动机指示转矩，其中i为当前过量空气系数值；Tλ=1为当量燃烧时的发动机指示转矩。

在对比稳态工况及瞬态工况下ANN和MAP法预测结果时使用瞬时的转矩百分比偏差（δerror）来评估转矩预测准确度，如式（2）所示：

式中：Te为预测转矩；T为GT-Suite发动机输出转矩。

1.3 转矩预测闭环控制方法

所述2种方法预测得出的转矩均为估计指示转矩，而发动机指示转矩直接受缸内燃烧放热状态所影响。有效输出转矩则为指示转矩扣除附件消耗转矩和机械摩擦损失转矩后所得，为了能够更精确地控制发动机燃烧放热从而控制发动机的有效转矩输出，故将指示转矩设为发动机控制系统的控制目标。

在混合动力发动机中，由于HCU给出的是发动机指示转矩命令，而实际发动机有效转矩包含了发动机当前机械损失转矩、附件消耗转矩等，因此，在闭环控制的情况下，需考虑不同工况的不同损失，根据目标有效转矩和预测指示转矩进行目标指示转矩和预测有效转矩的计算。指示转矩、预测转矩及各类转矩损失间的关系在本模型中简化为式（3）所示：

式中：Ti为指示转矩；Te为有效转矩；Tf为摩擦消耗转矩；Ta为发动机附件消耗转矩。

在根据发动机实际状态完成转矩估计的情况下，可以建立以预测转矩为接口的发动机控制方法（见图8）。由于发动机在不同工况下的各类损失情况不同，需要根据当前发动机状态进行转矩的协调计算，从而提高工况切换或者瞬态工况下的转矩预测准确性。图8中该转矩协调计算模块的主要功能有2个：①计算发动机当前机械损失转矩、附件消耗转矩；②根据目标有效转矩和估计指示转矩计算目标指示转矩和估计有效转矩。

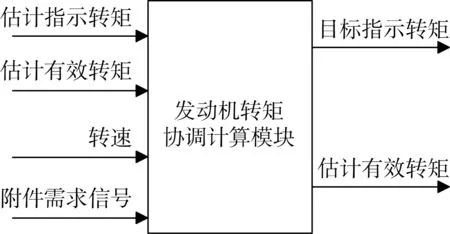
图8 转矩协调计算模块Fig.8 Schematic diagram of torque coordination calculation

对于机械摩擦和附件消耗转矩可以依据万有工况用发动机台架测定并形成对应的标定MAP，其输入量为当前发动机转速及目标负荷。在模型计算逻辑中计算预测的有效转矩时，当前查表MAP的目标负荷用控制目标指示转矩代替，当反馈修正有效转矩时，当前负荷则用预测指示转矩替代。

此外，闭环的反馈信号需要与控制的前馈MAP信号整合叠加，从而形成发动机时序性的控制信号，与反馈逻辑类似。图9为本模型方法对进气部分的前馈控制。模型中利用发动机的DVVT系统建立了进气门、排气门、旁通阀及节气门的前馈MAP，最终模型可以实现将发动机转矩的预测值作为转矩控制系统的反馈信号进而对进气系统执行器进行反馈控制。完整的进气协同反馈控制流程图如图10所示。图中的NA WOT 阈值设置为旁通阀及节气门全开工况下的转矩，可视作该发动机自然吸气工况下的最大转矩，是自然吸气工况和涡轮增压工况的分界转矩。当目标转矩小于90%分界转矩时，节气门闭环控制，旁通阀全开；当目标转矩大于90%分界转矩且小于100%分界转矩时，节气门开环控制，旁通阀闭环控制；当目标转矩大于100%分界转矩时，节气门全开，旁通阀闭环控制。

图9 前馈控制信号Fig.9 Feedforward control signals

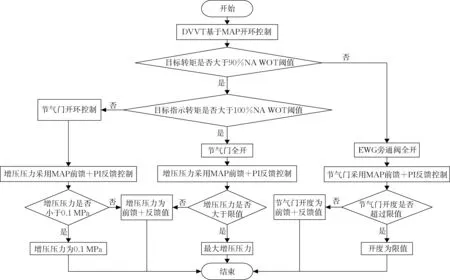
图10 进气协同反馈控制流程Fig.10 Intake collaborative feedback control process

2 仿真结果及分析

2.1 稳态工况转矩预测及误差分析

依据实际发动机工况，选取了低、中、高3 种不同转速作为转矩研究的典型转速，分别为1 000 r·min-1， 2 000 r·min-1和3 000 r·min-1。

针对发动机的稳态工况分别选取了50 N·m、100 N·m 以及150 N·m 作为目标转矩的研究对象，模拟的时长设定为从发动机起动开始的10 s 时间段。图11所示为模拟的10s时长、2 000 r·min-1转速下的稳态有效转矩的跟随性和稳定性曲线。

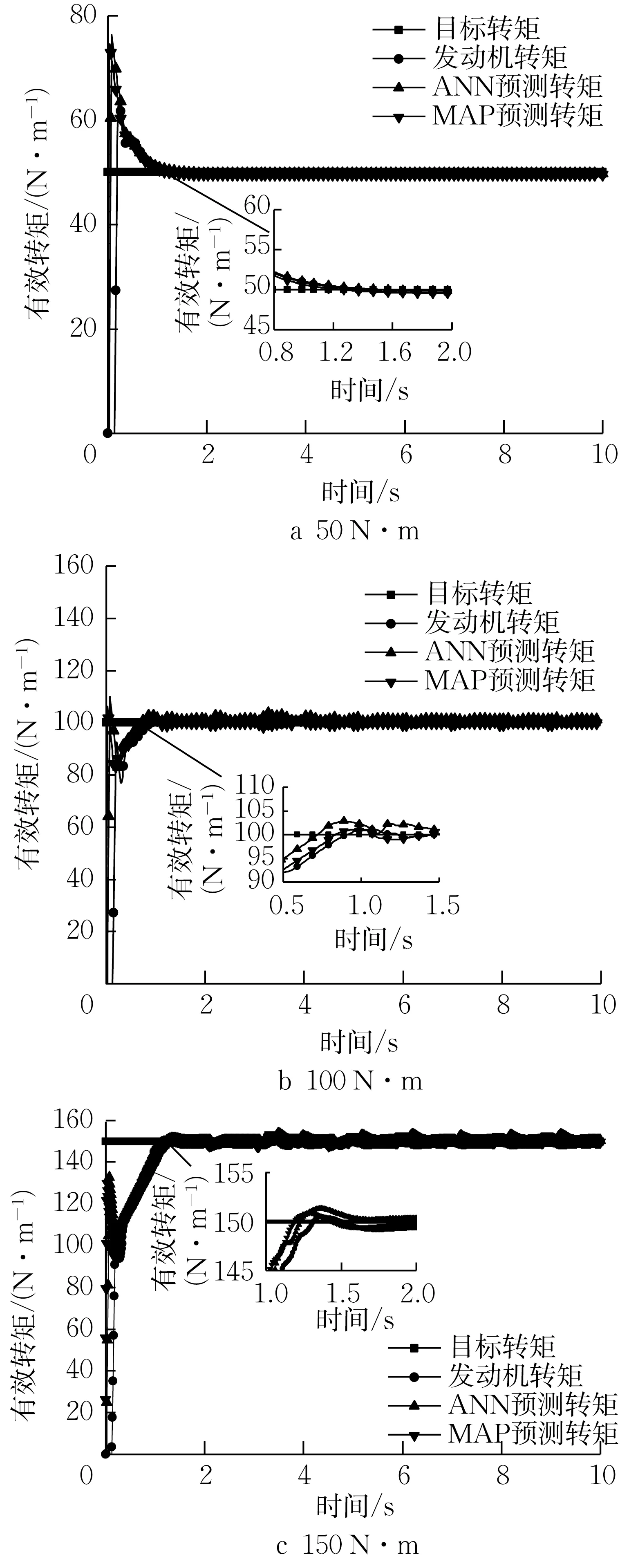
图11 稳态工况有效转矩曲线Fig.11 Break torque under steady working conditions 50 N·m, 100 N·m, and 150 N·m

图11 中的曲线分别代表目标设定的有效转矩（HCU转矩命令）、GT-Suite模型模拟的发动机有效转矩、ANN和MAP2种方法预测并计算得到的有效转矩。可以看出从发动机起动开始，预测转矩与实际曲线需要一定时间从零抬升至目标转矩附近。图11a中转矩50N·m对应的曲线抬升阶段波动幅度较小，这可能由于小转矩工况下的发动机控制参数与信号更为稳定性有关。

按照式（2）可计算预测的有效转矩的误差。为保证误差计算的合理性，计算过程去除发动机起动第1 s 的转矩不稳定阶段。分别通过对比GT-Suite模型运算得到的发动机实际转矩，ANN 和MAP 法的计算误差分析如图12。

图12 稳态工况预测转矩误差Fig.12 Errors of estimated break torque under steady working conditions at 1 000r·min-1, 2 000r·min-1, and 3 000r·min-1

图12包含了3种选区的不同转速下的误差计算分析。在稳态转矩模拟9种工况得到的误差中，有7种工况条件下MAP法预测精度低于ANN法，因此，MAP法更适用于各类转速的稳态转矩预测，各转速条件下不同转矩工况的累计误差分别较ANN 法低1.31%、1.09%和1.52%。

2.2 跃变及阶跃工况转矩预测及误差分析

在实际发动机运行过程中，维持长达数秒稳态的转矩的情况几乎不存在，HCU给定的目标转矩命令往往均以变化的形式出现。针对转矩跃变及转矩的阶段模拟结果如图13所示。

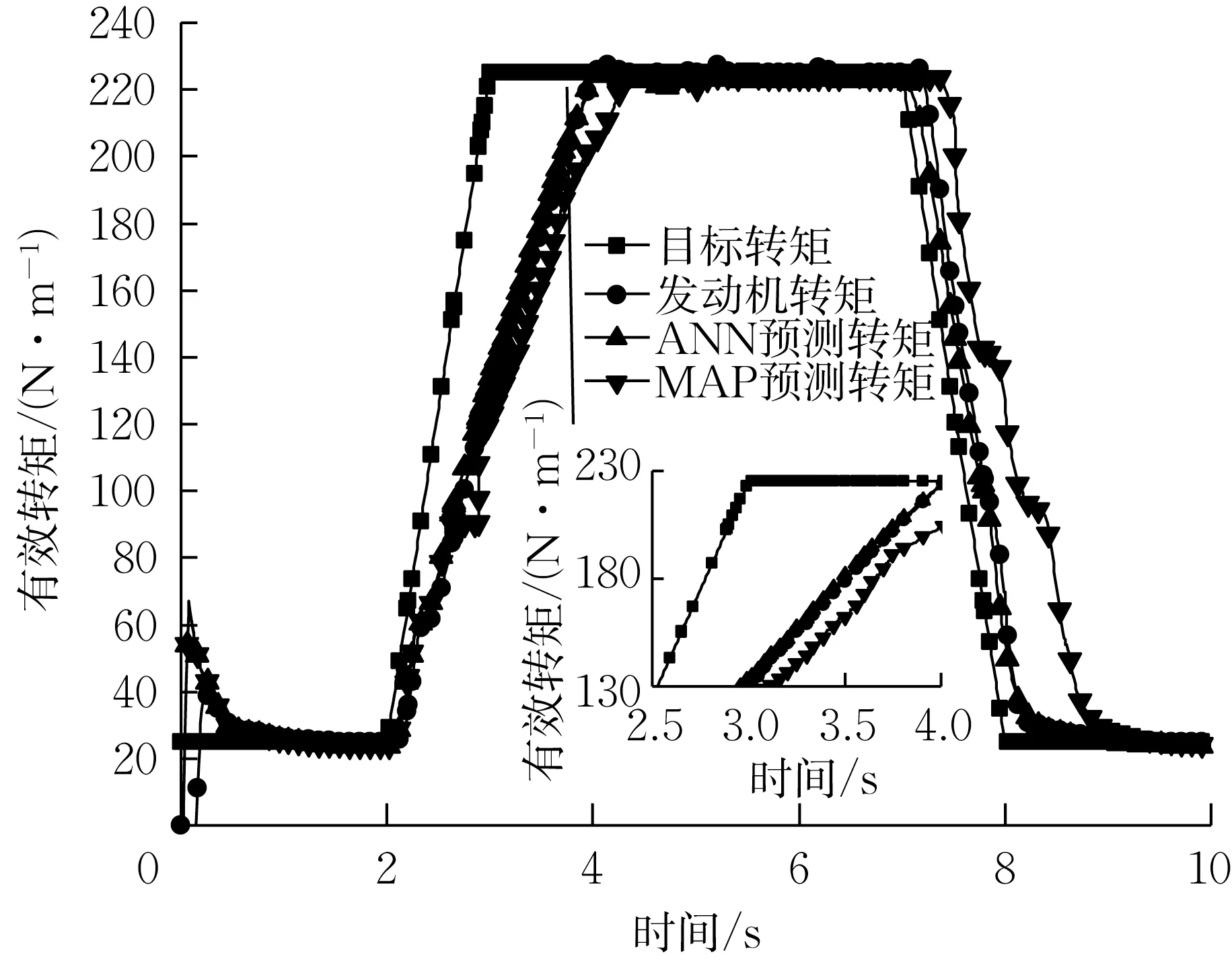
图13 2 000 r·min-1转速下跃变工况有效转矩Fig.13 Break torque under torque jump working condition at 2 000 r·min-1

不同转速下转矩跃变误差分析见图14。在转矩跃变瞬态工况下预测的各有效转矩曲线较稳态工况存在较为明显的差别，随着目标转矩以一定的斜率升高，GT模型模拟得到的发动机转矩及2种方法的预测有效转矩曲线都存在明显的时间延迟，这一现象也符合实际发动机的控制响应过程。从图中可以看出，MAP法由于其原理是根据发动机状态插值得到，因此预测得到的有效转矩曲线较ANN 延迟更大，依据图14的误差分析结果也可以看这一点。在瞬态工况转矩跃变条件下，ANN在各转速的预测精度显著高于MAP法，相比误差累计降低了5.62%。

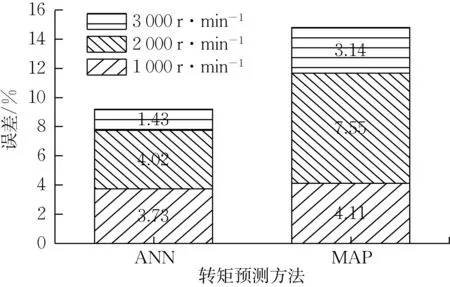
图14 跃变工况预测转矩误差Fig.14 Errors of estimated break torque under torque jump working conditions

图15 为不同转速下转矩阶跃模拟结果。图16为不同转速下转矩阶跃工况模拟结果误差分析。与跃变工况类似，转矩阶跃工况条件下发动机转矩与预测转矩也存在明显延迟，但是不同转矩提升幅度的阶跃工况对不同转矩预测方法的准确度几乎没有影响。从综合误差分析来看，ANN 法相比MAP 法在各转速下相对精准，误差相比MAP法低1.32%。

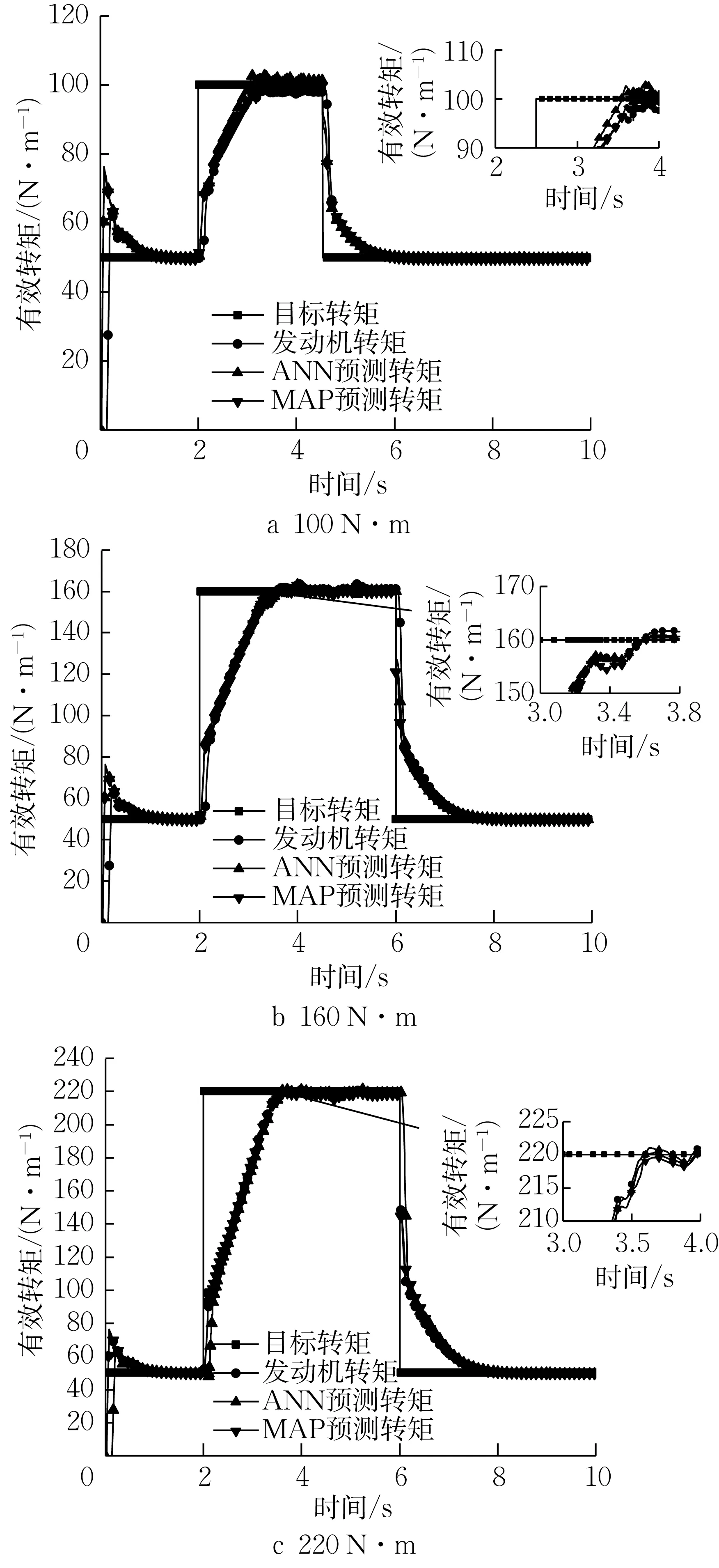
图15 2 000 r·min-1转速下阶跃工况有效转矩Fig.15 Break torque under torque step working condition at 2 000 r·min-1

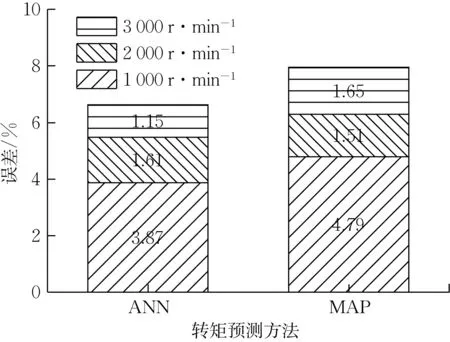
图16 阶跃工况预测转矩误差Fig.16 Errors of estimated break torque under torque step working conditions

2.3 升降挡工况转矩预测及误差分析

除了转矩的提升和下降以外，混合动力发动机瞬态工况常伴随着变速器升、降挡位。其中升、降挡过程要求发动机快速增减转矩，以达到良好的离合器结合控制；换挡完成后根据当前混合动力工作模式较为缓慢地调整输出转矩，实现较好的动力性和燃油经济性。

图17 所示为模拟的升挡工况转矩条件下的有效转矩曲线，其中目标转矩来源于发动机台架实际换挡过程中的测量结果。在升挡过程中，随着发动机起动，目标转矩先缓慢增加到80 N·m，在0.1 s时间内跌至30 N·m 并维持0.2 s，随后在0.5 s 时间内增加到140 N·m，之后继续缓慢增加。在升挡过程中，由于模拟进程较快，在换挡前的转矩缓慢上升阶段发动机转矩及预测转矩的跟随性较差，但在转矩快速下降时刻响应速度较好，发动机转矩及预测转矩发生的主要延迟范围表现在转矩二次上升时刻。

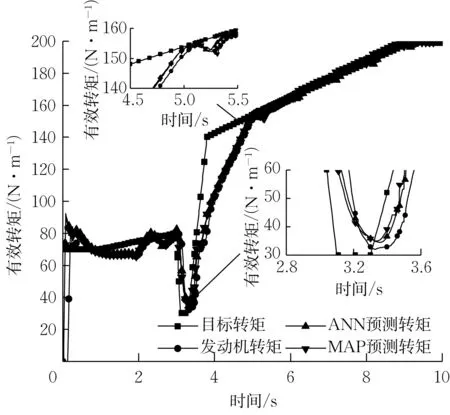
图17 2 000 r·min-1转速下升挡工况有效转矩Fig.17 Break torque under upshift working condition at 2 000 r·min-1

图18 为升挡工况预测转矩误差。综合来看ANN 法比MAP 法预测有效转矩的误差低1.93%。图19为模拟降挡工况转矩条件下的有效转矩曲线。在模拟降挡工况下，所控制的目标转矩先缓慢增加到110 N·m，在0.1s 时间内跌至30 N·m 并维持了0.2 s，随后在0.5 s 时间内增加到140 N·m，之后继续缓慢增加。降挡工况有效转矩曲线与升挡有所不同，由于转矩在大部分时间缓慢下降，因此发动机转矩及预测转矩对目标转矩的跟随性较好，可见的延迟发生在第1 次转矩下降及短时间稳定的阶段。

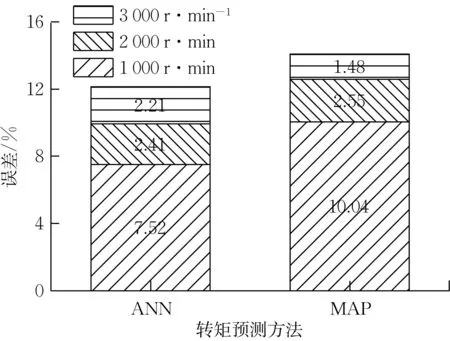
图18 升挡工况预测转矩误差Fig.18 Errors of estimated break torque under upshift working conditions

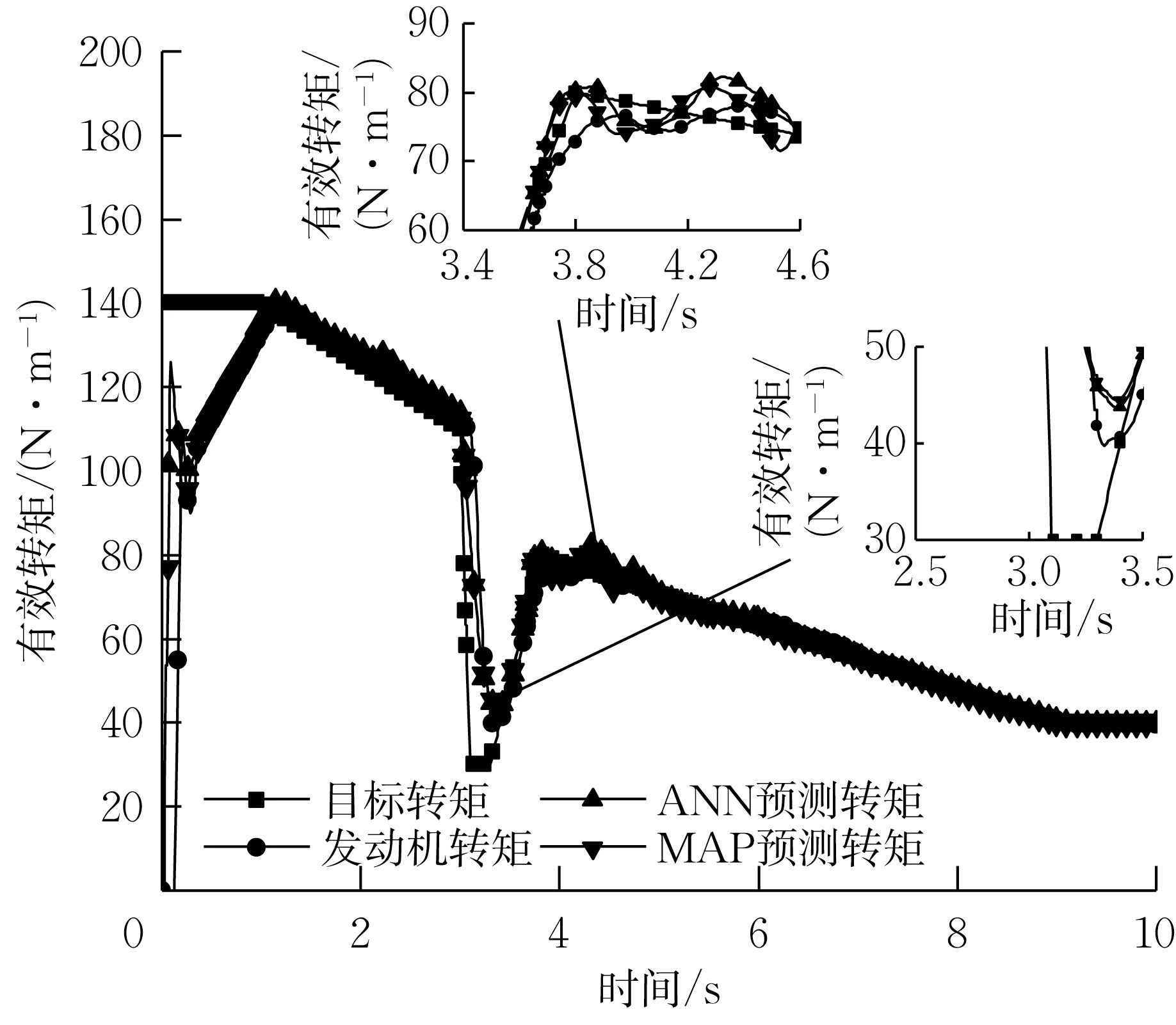
图19 降挡工况有效转矩曲线Fig.19 Break torque under downshift working condition at 2 000 r·min-1

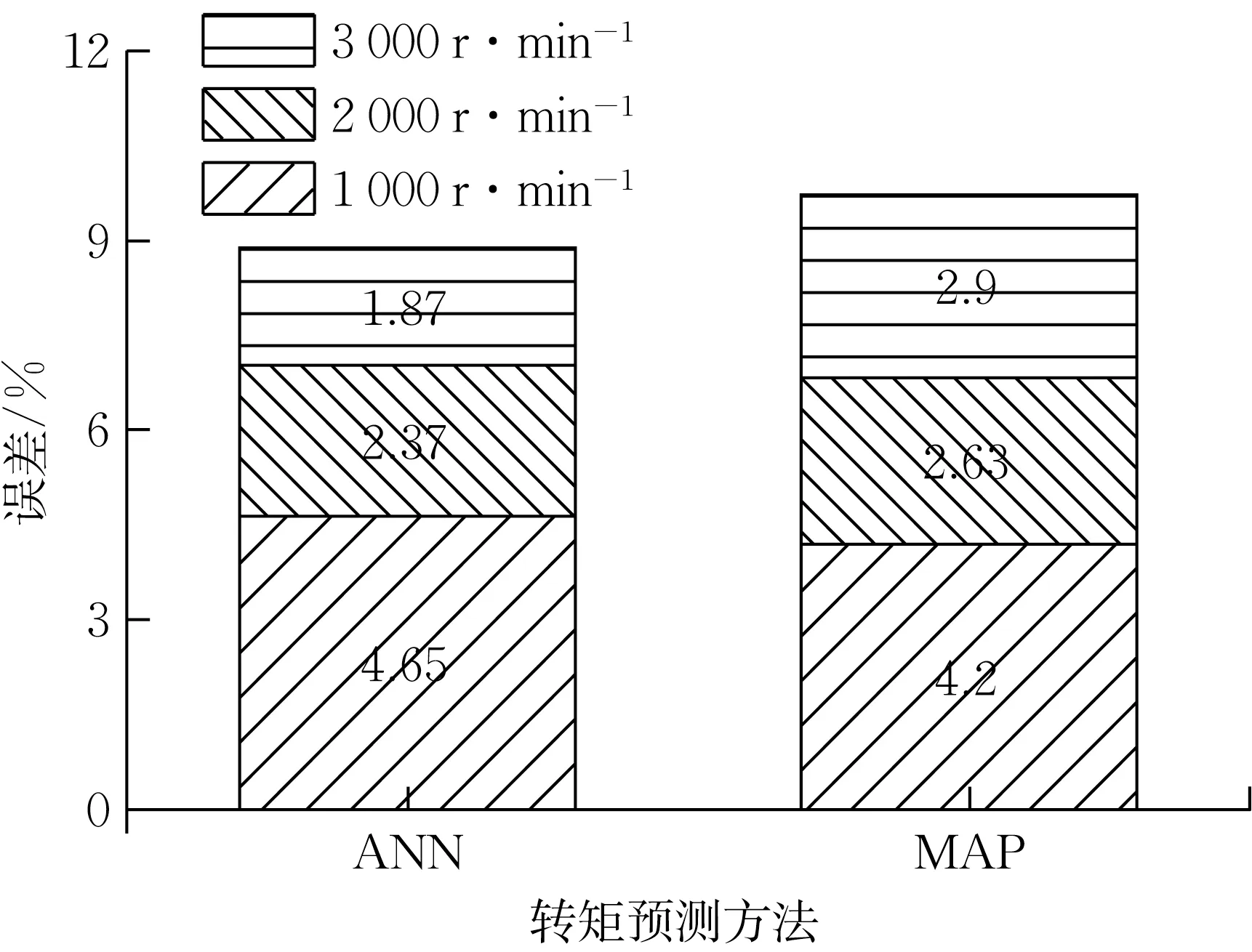
图20 降挡工况预测转矩误差Fig.20 Errors of estimated break torque under downshift working conditions

3 结论

基于搭建的GT-Suite 及Matlab/Simulink 联合仿真模型研究了ANN 方法对发动机稳态及瞬态转矩预测可靠性，建立了基于进气和发动机状态参数的预测转矩反馈协同控制模块，并对比了MAP法在同样条件下的结果误差。

由于稳态工况选取的转矩更加接近标定MAP的试验工况点，稳态工况下的MAP 法预测较ANN法更为精准，低、中、高3 种发动机转速下误差低1.31%、1.09%和1.52%，转矩预测波动范围较小。

在瞬态工况的跃变及阶跃的转矩变化条件下，MAP 法的预测延迟较ANN 法更为明显，相较于MAP 法的插值预测，更加密集的模型训练集对ANN法在工况切换过程中的预测精度有明显助益，ANN法预测所得到的有效转矩误差较MAP法分别低5.62%和1.32%。

在升挡工况及降挡工况下，ANN法的预测结果同样也更为精准，较MAP 法的误差分别低1.93%和0.84%。

稳态的发动机转矩预测利用标定好的MAP 进行插值更为适用，在瞬态工况下，ANN 法针对混合动力发动机的转速预测及控制有非常显著的潜在应用价值。

作者贡献声明：

楼狄明：项目/课题负责人，论文审阅与修改。

唐远贽：模型搭建，模拟数据，论文撰写与修改。

施雅风：概念提出，模型搭建，数据整理，论文撰写。

房 亮：概念提出，论文审阅与修改。

张允华：论文审阅与修改。

仇 杰：项目负责人，模型与试验数据提供。

杨 芾：项目/课题负责人，模型与试验数据提供。