面向多维特性数据的缺失值检测及填补方法对比

乔 非， 翟晓东， 王巧玲

（同济大学 电子与信息工程学院，上海 201804）

随着互联网、云计算等信息技术的发展，大数据日益渗透于金融、医疗、工业等各个行业领域之中，成为重要的生产因素，因此数据挖掘和应用具有十分重要的现实意义。在实际的采集、传输、存储过程中，多种原因导致数据质量参差不齐，导致后续数据分析挖掘效果也不佳［1-2］。现有大多数学者针对数据质量相关的研究主要集中在数据质量特性评估，侧重评估数据集的准确性、相似性或完整性，而这些特性分别取决于数据集中异常值、相似值及缺失值［3］。由于数据内在或外界因素而造成在某个属性上发生信息丢失的数据点称为缺失值。缺失值作为数据质量评估的重要方面，能够判断数据集中各数据的完整程度，为后续数据分析提供依据。在许多实际研究问题中，数据的缺失或不完整是必然存在的，当缺失数据占研究数据比重过大时会造成大量数据信息的丢失，导致基于数据的研究结果产生较大偏差，影响数据的使用效果。因此，对数据集的缺失值进行评估和研究是至关重要的［4-5］。

目前针对缺失值相关的研究主要包括缺失值检测和缺失值填补2 个方面。针对缺失值检测问题，由于大数据集具有维度高、数据量大的特点，目前研究多采用建模方法，根据数据点之间潜在的关联且不同数据属性之间也存在一定联系，建立缺失值检测模型，从而提高检测准确度并降低时间复杂度。例如，文献［6］研究了异构属性多维数组的概率建模，且使用拉普拉斯方法和高斯过程对近似的算法进行转换求解。该模型可以通过对海量数组的每个属性采用单独的指数族分布来管理异质性，从而对数据集的缺失值进行检测。文献［7］提出了一种快速检测丢失数据的方法，该方法概率性地对多类别RFID系统的丢失数据进行检测，在满足检测结果可靠的基础上，将检测时间最小化。文献［8］建立了2个回归适应模型，一个用于对缺失数据的主成分进行分析，另一个是根据缺失值构建的最小二乘回归模型，使用这2个模型，研究人员可以通过预测变量和响应变量推算出缺失值，从而实现对缺失值的检测。文献［9］采用Hollow-tree 方法来检测缺少属性值的数据，该方法首先定义出一组距离函数索引，这些函数可以测量缺失数据点之间的距离。其次，根据距离函数索引，计算出能够有效排序缺失数据而不会引起数据集内部结构失真的模型。最后，根据计算出的模型，对缺失数据进行检测。此外另有一些学者使用交叉验证模型，通过计算数据集的完整性实现对缺失数据的检测。例如文献［10］建立了完整性证据和不可信证据交叉验证模型，完整性证据用于检测数据的完整性，不可信证据用于判定缺失值检测的结果是否可靠。文献［11］首次提出采用IEC61970方法来进行信息集成，然后根据数据的特征自动建模，形成了一个可以直接进行判别缺失值的检测模型。文献［12］提出了一种基于复数旋转码的缺失值检验方法，该方法用哈希算法对数据进行交叉检验，但是仅针对细粒度数据，并不具有很好的通用性。

通过上述文献分析可知，目前针对缺失值检测方面的研究基本止步于对数据集是否含有缺失值进行判断，仅仅可以检测出数据集中含有缺失值的数据点，无法判断出多维特性数据点是多个属性维度还是仅一个属性维度发生缺失，且未对其缺失程度进行量化，缺少对多维特性数据全面立体的分析。另一方面，在机器学习和数据挖掘等大数据研究领域，为了能从数据集中提取到有用的信息，需要对缺失数据集进行处理，目前研究主要包括以下3 种方法：

（1）不作处理［13］。即保持原有带缺失数据的数据集，并对其进行信息挖掘，然而数据集中的维度缺失常常会导致数据类型不匹配的错误，这给后续数据分析与处理带来了挑战。此外，不作处理会导致缺失数据携带的信息价值丢失，从而造成数据分析结果不准确。

（2）删除数据［14］。删除数据是指将发生缺失的数据点进行删除，并把剩余未缺失的数据点重新归并为一个完整的数据集。该方法简单易行，在面对庞大数据集时仍能保持良好的时效性。然而也存在明显不足，缺失数据点往往携带实际生产过程中的相关重要信息，直接删除会造成数据价值浪费。虽然在缺失数据占少量比例的情况下，删除数据只会导致数据信息挖掘不完全，但是在数据集缺失程度严重、缺失数据所占比例大的情况下，直接删除缺失数据会造成整个数据集分布完全失真，从而不再具有研究价值。

（3）填补数据［15］。填补数据是指利用各类算法模型，基于数据点的分布情况，对缺失数据进行可能值填补，从而得到完整的数据集。该方法可以尽可能地挖掘出缺失数据所含信息，并提高了数据集的完整度，还原了数据集原始的空间分布。目前缺失值填补方法可分为如下4类：

一是固定值填补［16］。固定值填补是用特定数值对缺失值进行填补。一般都取零为特定数值。该方法能够有效快速对大数据集进行处理，避免在后续数据分析过程中出现数据类型不匹配的问题。然而固定值填补无法挖掘出缺失数据所蕴含的价值信息，并且对数据集的分布造成一定的影响。

二是替换缺失值［17］。替换缺失值是指用一些数学方法，参考缺失值所在位置的上下文计算得到缺失值的可能取值。常用的方法有：平均值填补、中位数填补、众数填补、插值填补等。

三是模型填补［18］。模型填补是利用其他完整数据点对缺失值预测模型进行训练，将缺失数据点输入到预测模型，得到缺失位置的可能填补值。常见的如KNN（k-nearest neighbor）算法模型、Iterative Imputer算法模型等。

四是低秩逼近［19］。低秩逼近通过将数据集转换为矩阵形式，构建合理的低秩矩阵模型，通过低秩矩阵优化算法求解最优解，从而填补缺失值，目前多应用于高缺失程度情况下的缺失值填补［20］。

在实际应用过程中，不同情况下对缺失值填补算法的要求往往不同［21］。例如当数据集的缺失程度小、数据分析精度要求低时，往往使用固定值填补方法，从而实现快速填补。当数据分析精度要求较高、缺失程度较大的情况下，使用模型填补能够挖掘出已有数据点之间的联系，从而预估出缺失值。但目前上述3 类方法都包含多种缺失值填补方法，如何根据数据集的缺失程度选择最合适的填补方法仍有待研究。

综上所述，由于数据集结构多样，生产采集环境复杂，经常会发生数据点的缺失。尽管目前针对数据集中缺失值检测及填补方法已经具有一定的研究，由于数据处理分析过程中对数据质量的要求不断提高，针对多维特性数据的缺失值检测及填补方法研究也变得更加复杂和具有挑战性。本文研究主要包括以下两点：

（1）考虑到目前常见的多维特性数据，由于其不同属性维度的缺失都会对数据质量造成影响，所以首先针对多维特性数据缺失程度分析不够全面、基本止步于对数据集是否含有缺失值这一不足展开研究［9］，设计缺失值检测方法，在数据点缺失度基础上进一步提出数据总体缺失度和加权数据总体缺失度2个概念的严格定义及计算公式，实现对多维特性数据集缺失程度的全面检测，为后续缺失值填补方法的选择提供理论依据。

（2）目前已有缺失值填补方法众多，但多数研究所关注的问题一方面是对某种缺失值填补方法本身的精度进行改进［22］，另一方面是对缺失值进行简单填补从而得到更加准确可靠的数据分析结果［23］，忽略了所选择的缺失值填补方法是否合适。针对该问题，基于所提出的3种缺失度通过实验横向、纵向对比和分析不同缺失值填补方法性能，研究不同缺失值填补方法的适用性，从而实现根据数据集的缺失程度选择最合适的填补方法，进一步提高后续数据处理分析的准确性和可靠性。

1 缺失值检测方法设计

当对数据集的缺失程度进行分析时，首先需要对其进行缺失值检测。在实际生产过程中，数据集中的每个数据点往往具有多个属性维度，在空间中具有复杂的形态，采用Dataframe格式［24］对数据集进行存储。DataFrame 是一种表格型数据结构，它含有1 组有序的列，每列可以是不同的值，既有行索引，也有列索引，数据点的分布更为直观，方便进行缺失值检测。所设计的缺失值检测流程如图1 所示，具体步骤如下。

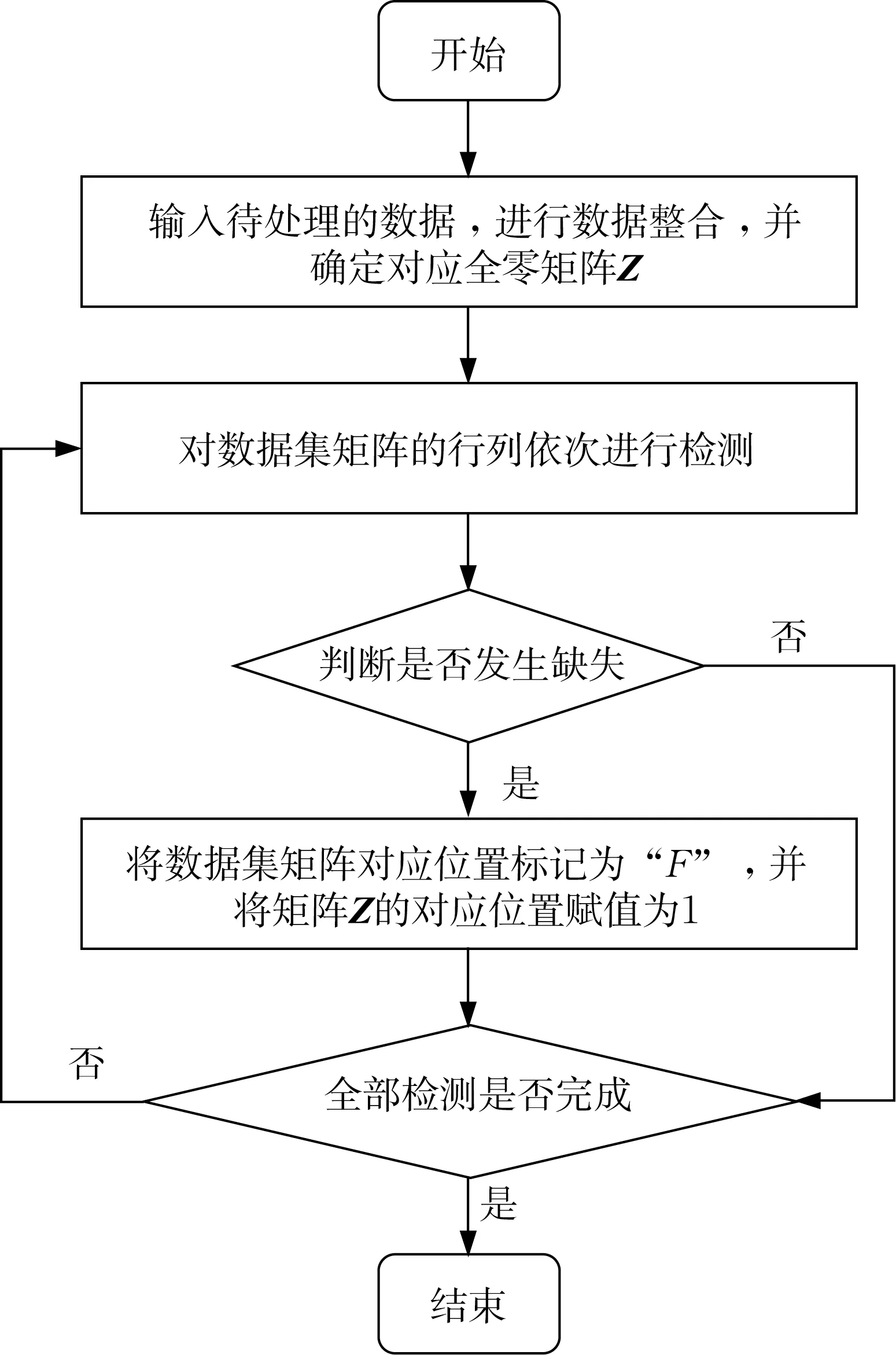
图1 缺失值检测流程及伪代码Fig.1 Flowchart and pseudo-code of missing value detection

（1） 输入待处理的数据集D1，并将其整合成n×m阶矩阵，其中n代表数据点的数量，m代表每个数据点的维度，每个元素为xij（其中i表示矩阵行数，j表示矩阵列数）。

为了更直观说明，这里采用一组6×4阶数据集D'1进行举例描述。设数据集D'1有6个数据点，每个数据点包含4个属性维度。根据数据集D'1的分布可以看出，第1个和第5个数据点发生了缺失。

（2） 定义n×m维全零矩阵Z0从矩阵的第1行第1 列即i=1、j=1 开始在空间中对数据集矩阵的行列依次进行检测，并判断每一个数据点xi（0＜i≤n，i∈N）的每一个维度xij（0＜j≤m，j∈N）是否为空。若判断出xij为空，则将数据集矩阵的第i行第j列标记为“F”，即xij=F，并为矩阵Z的第i行第j列赋值为1，即Z［i，j］=1，表明xij发生缺失。反之，则不填充。

（3） 重复进行步骤（2），直至对整个数据集D1完成检测。如图2 所示，此时Z矩阵标记完毕，从空间上直观给出了数据集的缺失分布，被标记为1 的表明数据点在相应维度发生了缺失。

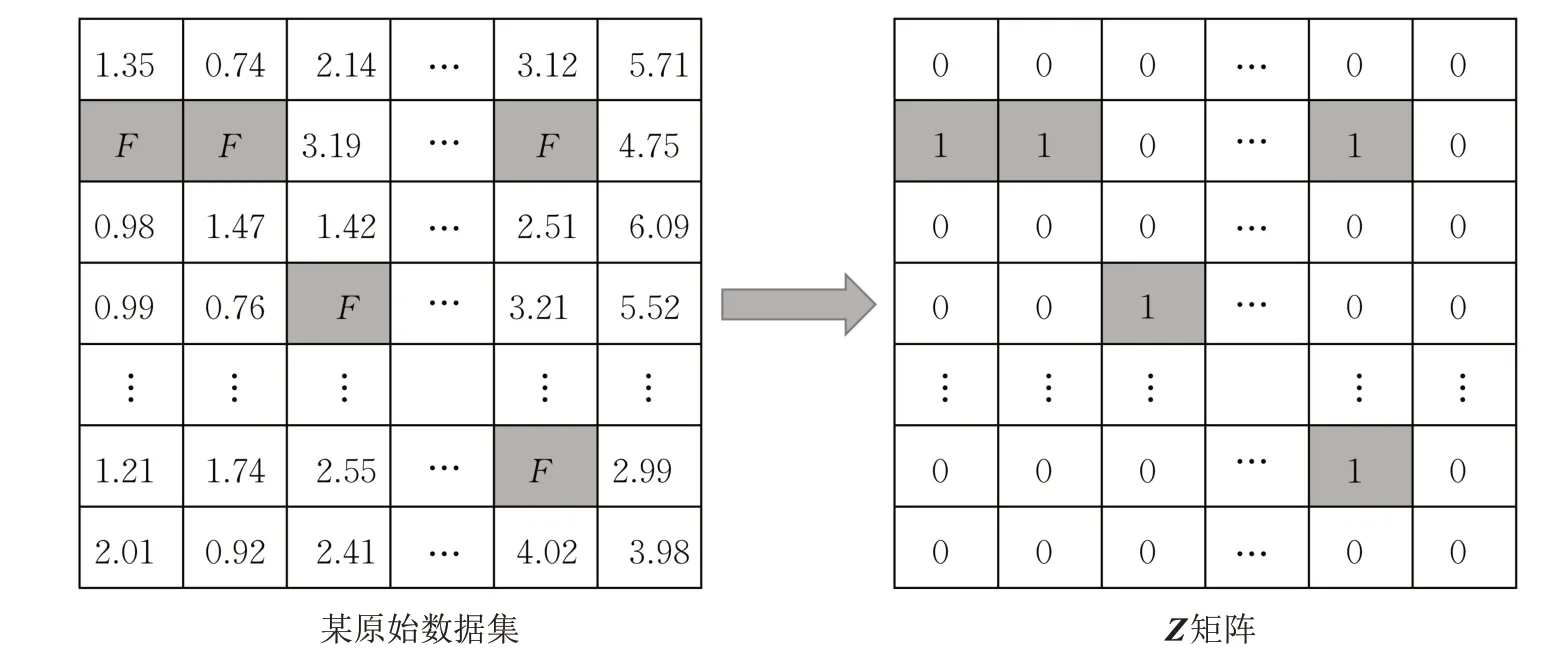
图2 矩阵Z示意Fig.2 Schematic diagram of matrix Z

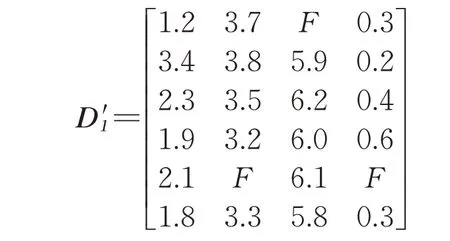
图3 缺失值检测后数据集矩阵示意Fig.3 Schematic diagram of dataset matrix after missing value detection

相应地，对数据集D'1检查完后，对应的D'1及其Z矩阵为

利用上述缺失值检测方法能够查找出数据集中发生缺失的数据点的位置及缺失属性的个数。接着基于该缺失值检测方法提出多种缺失度概念，根据缺失值检测结果对数据集的缺失度进行计算，从而客观全面地反应整个数据集的缺失程度。

2 多维特性数据集缺失度

数据缺失会造成数据集携带信息的损失，需要对数据集的缺失程度进行评估，以便研究人员全面直观地了解数据集。而数据缺失可能有数据点缺失、属性维度缺失［25］等，因此有必要结合数据的多维特性对数据集进行缺失度评估。针对该问题提出数据点缺失度、数据总体缺失度和加权数据总体缺失度3个概念。

2.1 数据点缺失度

数据点缺失度用于衡量整个数据集中具有缺失的数据点占所有数据点的比重，记为“Mall”。如图4a所示，该数据集中第2行和第i行的数据点分别在不同维度发生了缺失，即存在数值为“F”的项，因此把第2个和第i个数据点标记为缺失数据点，数据集总体缺失2个单位。

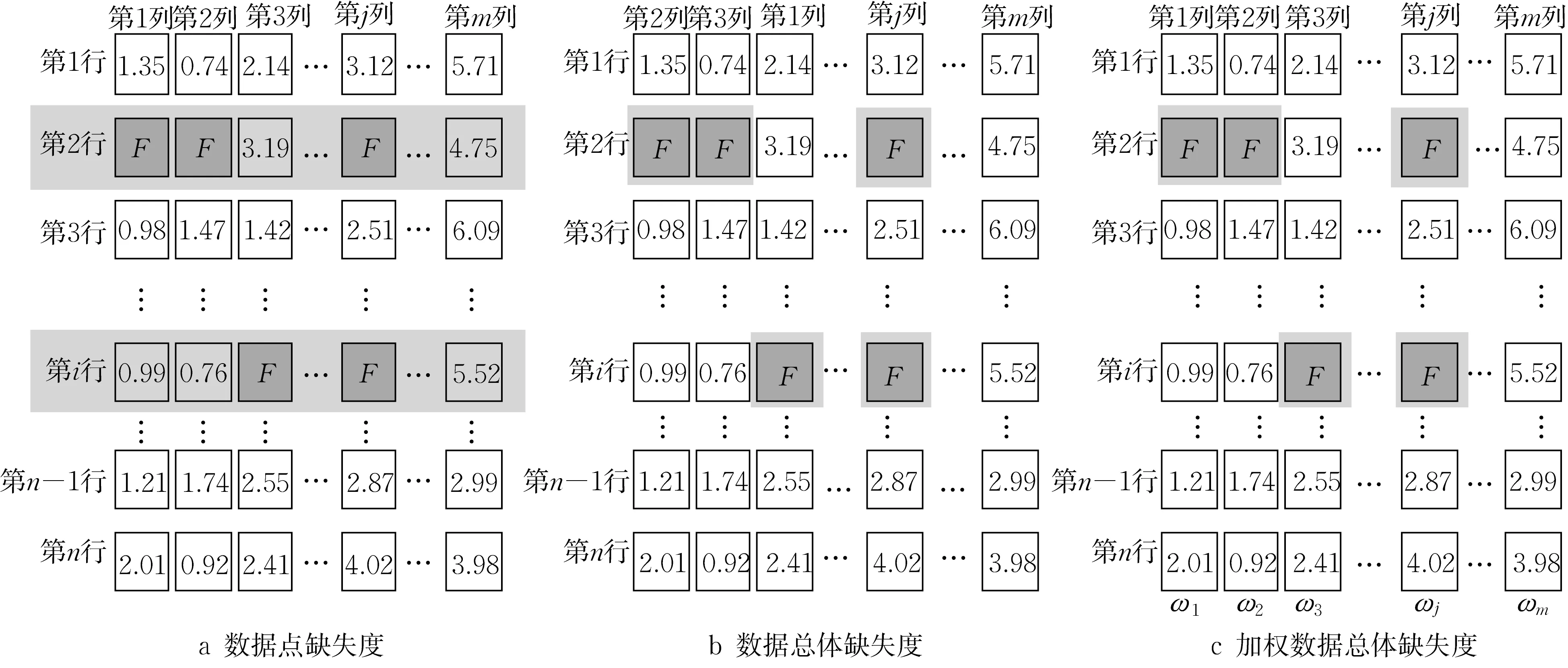
图4 3种缺失度示意Fig.4 Diagram of three missing degrees

数据点缺失度的具体计算方法如下：

（1）统计缺失数据点总个数。首先定义Sdata为缺失数据点的总个数，从第1 行开始，依次对Z矩阵的每一行进行各个维度的求和，若某一行所有维度总和相加为零，则表明该行维度全为零，即该数据点在任意维度上都没有发生缺失，反之，若Z矩阵的第i行各个维度之和不为零，表明第i个数据点发生了缺失，则对Sdata进行加1。

（2）计算数据集数据点缺失度。数据集数据点缺失度（Mall）计算公式为

式中：row（Z）表示Z矩阵的行数，即数据集所包含数据点的总个数。

数据点缺失度侧重于计算整个数据集中发生缺失的数据点所占的比重。其有效考察了含有缺失值的数据点个数，反应了数据集在整体上的缺失程度。

2.2 数据总体缺失度

在大数据背景下一个数据点往往会在多个属性维度发生缺失。倘若只根据数据点缺失度对缺失数据点的个数及其所占的比重进行判断，则较为片面。为了更全面地为数据集缺失质量提供理论支撑，提出数据总体缺失度（Mmen）这一概念。与数据点缺失度不同，数据总体缺失度的最小单位为数据点的一个属性维度，而非一个数据点。数据总体缺失度用于衡量整个数据集中发生缺失的属性维度占总属性维度的百分比。如图4b所示，该数据集中第2行的第1、2、j列以及第i行的第3、j列为F，因此，第2个数据点在1、2、j这3个属性维度上发生了缺失，第i个数据点在3、j这2个属性维度上发生了缺失，数据集总体缺失5个属性维度单位。

数据总体缺失度Mmen的计算式为

式中：Z［i，j］表示矩阵Z的第i行、第j列。通过对整个数据集中各个数据点的各个属性维度上的数字进行求和，即可得知整个数据集中发生缺失的属性维度总个数。再将缺失属性维度总个数与数据集中数据点所有维度总和m×n求商，从而得到数据集中发生缺失的属性维度占数据总体的百分比，即数据集的数据总体缺失度。

2.3 加权数据总体缺失度

在生产过程中，数据集的每一属性维度对企业管理人员的参考价值往往不同。例如根据设备的电流、电压参数监测设备的健康状况时，电流和电压2个属性维度的数据相对温度、湿度等其他数据来说更为重要，即当数据点在电流、电压属性方面发生缺失，会比在其他属性缺失造成更严重的影响。因此，为数据集的每一属性维度设定权重比例系数，并引入加权数据总体缺失度（Mw），从而更加灵活全面描述数据集的缺失度，更能符合实际需求。

式中：Z［i，j］表示矩阵Z的第i行、第j列。依次对每一个数据点的每一属性维度进行检测，并与该维度对应的权重系数相乘，从而求得该数据点的加权缺失度，再将所有数据点的加权缺失度求和，并与数据集中数据点所有维度总和m×n求商，从而得到数据集的加权数据总体缺失度。

3 面向多维数据的缺失值填补算法及对比分析

在机器学习和数据挖掘研究领域，为了能从数据集中提取到有用的信息，对含有缺失值的数据集进行处理是非常必要的，但如何从众多的缺失值填补算法中选择合适的方法仍有待研究。本文基于提出的多种缺失度概念和公开数据集对多种不同典型的缺失值填补算法进行性能评估，采用多种评价指标研究不同缺失值填补方法在各种缺失度情况下的适用度。

3.1 实验数据集

从常用机器学习数据库UCI Machine Learning Repository［26］中选取Iris数据集进行实验，Iris共包含150 个样本数据点、4 个属性维度，所有的数据点被分为3个类。

实验从数据点缺失度和数据总体缺失度的大小关系出发，评价缺失度对填补算法性能的影响。实验一共设置5组不同缺失程度的对比数据集：20-05、20-15、40-15、60-15、60-45。表1 介绍了数据集的具体信息，列举了每个数据集发生缺失的数据点个数、发生缺失的属性维度个数、数据点缺失度和数据总体缺失度这4 个属性。例如20-15 表示用随机方法构建数据点缺失度为20%、数据总体缺失度为15%的数据集，该数据集发生缺失的数据点个数为30个，发生缺失的属性维度个数为90 个，平均每个数据点在3个属性维度上发生了缺失。

表1 数据集介绍Tab.1 Introduction to dataset

根据上述缺失度的设置，这些数据集囊括了Mall偏小且Mmen偏小、Mall偏小且Mmen偏大、Mall中等且Mmen中等、Mall偏大且Mmen偏小，以及Mall偏大且Mmen偏大这5 种情况。后续实验在这5 组数据集的基础上，对5种缺失值填补算法进行全面性能评估。

3.2 算法性能评价指标

采用典型的F1-score和RMSE2个指标来评判多种缺失值填补算法的性能。F1-score能有效判断预测分类和实际分类的相似程度，是预测模型精确率和召回率的一种加权平均。RMSE计算了预测结果与真实结果的均方根误差，用于进一步衡量缺失值预测结果是否接近真实结果。表2 为预测模型的混淆矩阵，其包含了模型预测的4种结果：在真实结果为0的情况下，若预测结果也为0，则表示真负例（true negative，TN），若预测结果为1，则表示假正例（false positive，FP）；在真实结果为1的情况下，若预测结果也为1，则表示真正例（true positive，TP），若预测结果为0，则表示假负例（false negative，FN）。

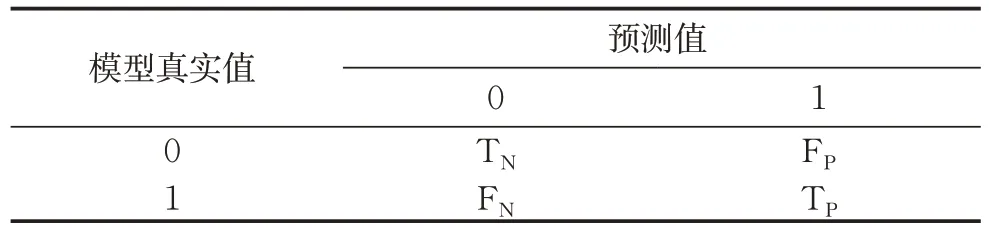
表2 混淆矩阵Tab.2 Confusion matrix

根据模型预测的结果可以得到该模型预测的精确率Precision和召回率Recall，具体计算公式为

式中：NTP表示真正例的个数；NFP表示假正例的个数；NFN表示假负例的个数。精确率表示被正确预测为1的样本占预测为1的样本总数的比例；召回率表示被正确预测为1 的样本占真实为1 的样本总数的比例，F1-score为精确率和召回率的调和平均数。

F1-score的范围为［0，1］，根据式（7）可以看出，精准率和召回率只要有一个比较小的话，F1-score的值都会降低，即F1-score越大表明预测结果越好。

实验采用的另一个评价指标为RMSE，具体计算式为

式中：ei为原始未发生缺失的数据；e͂i为发生缺失后进行填充的数据；m为缺失维度总个数。RMSE值越大，表明误差越大，缺失值填补算法的预测效果越不好。

综上所述，F1-score是用于评判模型预测缺失值的准确度，而RMSE是用于评判模型累计预测误差值。

3.3 缺失值填补算法

目前常用的缺失值填补方法可分为固定值填补、替换缺失值和模型填补的方法，为了对不同填补方法在不同缺失度时填补效果进行全面评估，从固定值填补方法里面选择补零法，从替换缺失值方法里选择平均值和插值填补方法，从模型填补方法里选择KNN填补和Iterative Imputer填补算法，基于提出的缺失度概念对这5种典型的缺失值填补算法进行性能比较。需要说明的是，上述5 种常见方法多应用于数据点缺失度不超过60%的情况，当缺失度过高时，由于算法原理的原因，上述算法无法达到良好的填补效果，此时可选择低秩逼近方法［20］。实验中5种缺失值填补方法具体介绍如下：

（1）补零法［27］。将检测出的缺失数据全部填充为零。

（2）平均值填补［28］。将缺失数据所在维度的其他所有数据求平均，用平均值对该维度所有缺失值进行填补。

（3）插值填补［29］。插值填补是基于拟合函数的一种填补方法，其具体思想为：根据数据集中未发生缺失的完整数据点求取出插值函数，再对缺失值进行预测，并将预测值作为缺失值的可能填补值。

（4）KNN 填补算法［23］。KNN 填补算法是基于数据点之间的相似性来达到填补缺失值的目的。具体步骤为：① 设定最近邻个数K值；② 在特征空间中，根据欧氏距离判断出与缺失值距离最近的K个相邻数据点；③ 依次对这K个相邻数据点的类别进行判断，统计出这些相邻点所属的类别，并确定包含最多相邻点的类别。④ 根据这整个类的特征利用预测模型对缺失值进行填补。

（5）Iterative Imputer 填 补 算 法［30］。Iterative Imputer是以循环的方式实现建模预测缺失值的，具体步骤为：①指定一个维度作为输出值y；② 其他剩余维度均作为输入值x；③ 根据x和y对回归预测模型进行训练；④ 利用训练好的模型预测出维度y上的所有缺失值。⑤重复步骤①-④，循环更新维度作为新的输出值y，直至完成所有维度的缺失值填补。

实验所采用的算法参数说明如下：补零法、平均值填补、插值填补为基于统计信息的填补方法，不存在超参数的设置。KNN填补算法中存在超参数“聚类个数k值”等，Iterative Imputer 填补算法中存在超参数“迭代次数”等。需要说明的是，实验目的是为了对比分析不同缺失值填补算法在数据集不同缺失度时的效果，而上述算法中超参数选择的不同会同时影响该算法在不同缺失度下的填补效果，即超参数选择越合理，该算法在不同缺失度下的填补效果越高。此外，考虑到目前研究中选择KNN 和Iterative Imputer方法对缺失值进行填补时均会优化对应超参数，进行实验时也对KNN 和Iterative Imputer方法中的超参数根据实验结果进行了优化，选择最优的实验结果对应的超参数；同时为了消除实验结果偶然性的影响，对含有超参数的KNN 和Iterative Imputer 方法进行5 次实验，对应的实验结果为多次结果的平均值。综上所述，实验结果具有普遍性，超参数的选择不影响实验结论。

3.4 同种算法在不同缺失度情况下的性能对比

根据上述5种缺失值填补算法和数据集进行实验，5种填补算法在不同缺失程度数据集上的填补效果如图5所示。

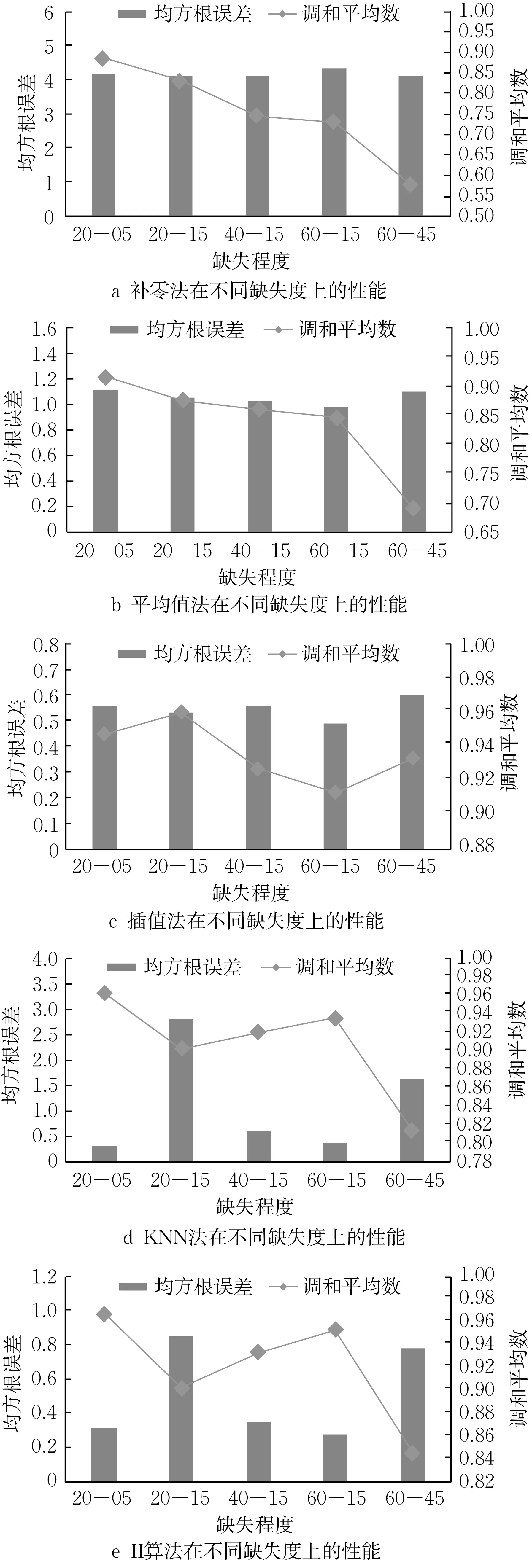
图5 5种算法在不同缺失度时的填补结果Fig.5 Imputation results of five algorithms at different missing degrees

图5a为补零法在数据集5种缺失情况下的性能指标分析：① 对不同缺失程度的数据集来说，RMSE指标相差不多，表明补零法的预测填补值误差在5 种缺失情况下效果较为接近；②F1-score指标按照Iris20-05、Iris20-15、Iris40-15、Iris60-15、Iris60-45 的顺序依次降低，表明填补的准确度逐步下降。③ 总体来说，数据点缺失度越大，补零法对缺失值的填补效果越差；在数据点缺失度相同的情况下，数据总体缺失度越大，补零法效果越差。数据点缺失度比数据总体缺失度对补零法的影响大。

图5b为平均值法在数据集5种缺失情况下的性能指标分析：① 对不同缺失程度的数据集来说，RMSE指标相差不多，表明平均值法的预测填补值误差效果较为接近。②F1-score指标在Iris20-05 数据集上最好，按照Iris20-15、Iris40-15 和Iris60-15 的顺序略有降低。在Iris60-45 数据集上最差，表明预测的填补值与真实情况最不接近。③ 总体来说，数据点缺失度越大平均值法对缺失值的填补效果越差；在数据点缺失度相同的情况下，数据总体缺失度越小，平均值法效果越好。数据点缺失度比数据总体缺失度对平均值法的影响大。

图5c为插值法在数据集5种缺失情况下的性能指标分析：① 5 个不同缺失程度数据集的RMSE指标都比较小，数值在0.55 左右，且相差不多。表明插值法对于这5个数据集的预测填补值与真实值都比较 接 近。② 按 照Iris60-15、Iris40-15、Iris60-45、Iris20-05、Iris20-15 的顺序，数据集的F1-score指标的结果值逐渐变好，表明预测填补值与真实情况逐渐接近。③ 比较数据点缺失度相同、数据总体缺失度不同 的 数 据 集 组Iris20-05 和Iris20-15、Iris60-15 和Iris60-45可知，数据点缺失度相同的情况下，数据总体缺失度越大，数据集的F1-score指标值越好。因为数据集本身分为3 类，每个类别的数据点之间差异性较大，若拟合出一个插值函数来形容数据集中的所有数据点，误差比较大。而数据总体缺失度较大的数据集Iris20-15 和Iris60-45 中，平均每个数据点缺失3 个属性维度，这种情况下不同类别的数据点之间的差异性变小，因此插值法拟合出的函数能较好地表示整个数据集的特点。④ 数据集Iris20-05缺失数据点较少，类别之间差异性明显；数据集Iris60-15缺失数据点过多，无法拟合正确函数，因此插值法对这2种低数据总体缺失度的数据集填补效果相对不佳。⑤ 总体来说，在数据点缺失度相同的情况下，数据总体缺失度越大，插值法填补效果越好。

图5d 为KNN 填补算法在数据集5 种缺失情况下的性能指标分析：① 数据集Iris20-05、Iris40-15、Iris60-15的RMSE指标相差不多，Iris20-15的RMSE值最差，表明KNN在Iris20-15数据集上预测填补值与真实值误差最大。②F1-score指标在Iris20-05 数据集上最好，数据集Iris60-15 其次，数据集Iris60-45 最差。③ 总体来说，在数据点缺失度相同的情况下，数据总体缺失度越大，KNN 对缺失值的填补效果越差。数据总体缺失度比数据点缺失度对KNN 填补法的影响大，这是因为KNN算法是根据缺失点的最近K个数据点所属的类别进行判断的，当数据总体缺失度过大时，每个数据点均有多个属性维度发生缺失，数据点的特征性不明显，KNN无法准确判断数据点所属的类别，导致预测的填补值不准确，误差较大。

图5e为Iterative Imputer填补算法在数据集5种缺失情况下的性能指标。由于Iterative Imputer算法和KNN 算法的填补思想皆为通过统计未缺失数据点的类别来确定缺失数据点的特征并进行填补，因此这2种填补算法的分析结果类似。

3.5 不同算法在同种缺失度数据集上的性能对比

图6 进一步展示了在每种缺失度的数据集上5种不同算法的填补效果，从而系统地对每种填补算法的性能进行分析。

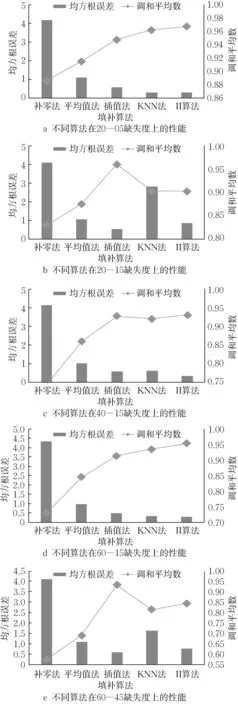
图6 相同缺失度下不同填补方法结果对比Fig.6 Comparison of different imputation methods at the same missing degree

图6a 为不同算法在20-05 缺失度上的填补结果。当数据集的数据点缺失度为20%、数据总体缺失度为5%时，补零法、平均值法、插值法、KNN 法、Iterative Imputer算法的缺失值填补效果依次变好。

图6b 为不同算法在20-15 缺失度上的填补结果。当数据集的数据点缺失度为20%、数据总体缺失度为15%时，补零法的填补效果最差，其次为平均值法和KNN 算法，Iterative Imputer 算法较好，插值法填补效果最佳。

图6c 为不同算法在40-15 缺失度上的填补结果。当数据集的数据点缺失度为40%、数据总体缺失度为15%时，补零法的填补效果最差，其次为平均值法，KNN 法的效果居中，插值法、Iterative Imputer算法的填补效果均比较好。

图6d 为不同算法在60-15 缺失度上的填补结果。当数据集的数据点缺失度为60%、数据总体缺失度为15%时，补零法的填补效果最差，平均值法、插值法、KNN法、Iterative Imputer算法的依次变好。

图6e 为不同算法在60-45 缺失度上的填补结果。当数据集的数据点缺失度为60%、数据总体缺失度为45%时，补零法的填补效果最差，其次为平均值法，KNN 算法的填补效果居中，Iterative Imputer算法较好，但插值法填补效果最佳。

由上述5 种情况分析可以得到如下结论：① 补零法和平均值法在各种缺失度下的填补效果均不好，因此仅可以在对填补精度要求不高时使用。②在数据总体缺失度不高的情况下，基于模型的KNN算法和Iterative Imputer 算法都能有较好的填补效果。KNN 和Iterative Imputer 都为基于预测模型的缺失值填补算法，但是Iterative Imputer 算法的性能总是优于KNN算法，因为Iterative Imputer算法是循环更改输入变量来训练缺失值预测模型，因此模型的误差更小，填补效果更好。③ 在数据总体缺失度较大的情况下，即单个数据点缺失属性维度较多的情况下，插值法具有最好的填补效果。综上所述，该实验可以证明，通过对数据集缺失度进行全面系统的评估可以对缺失值填补算法的选择起到良好的指导作用。

4 结语

从多维特性数据缺失值检测和填补工作切入，针对传统缺失值检测方法缺少对多维特性数据缺失程度全面立体的评估以及多种缺失值填补方法难以选择的问题，通过设计缺失值检测方法，在数据点缺失度基础上，提出数据总体缺失度和加权数据总体缺失度的概念，实现对数据集缺失程度的全面检测，进而通过实验横向、纵向对比和分析不同缺失值填补方法的性能。实验证明，补零法和平均值法在各种缺失度下的填补效果均不好，因此仅可以在对填补精度要求不高时使用。在数据总体缺失度不高的情况下，基于模型的KNN算法和Iterative Imputer算法都能有较好的填补效果，且Iterative Imputer 算法比KNN 算法性能更好。在数据总体缺失度较大的情况下，插值法具有更好的填补效果。综上所述，通过对数据集缺失度进行全面系统的评估可以对缺失值填补算法的选择起到良好的指导作用。

提出的缺失值检测和填补方法主要应用于具有多维特性的数据集，不适用于以树、链表等复杂数据结构表达的数据集，今后会考虑向复杂数据结构的缺失值检测和填补领域开展。此外，本文目前只考虑了对离线数据进行缺失值检测和填补，由于实际生产过程中也会有大量的实时数据产生，因此后续可以针对实时数据流设计相应的缺失值检测和填补方法。

作者贡献声明：

乔 非：研究工作思路与全程指导。

翟晓东：研究工作补充完善与总结。

王巧玲：初步研究工作。