基于广义S-D分配算法的船舶目标跟踪与航迹起始研究

周浚璠,丁 凯

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

基于船舶雷达的目标跟踪技术受到海上目标运动状态、外部环境噪声以及信号处理技术误差的影响,单雷达探测技术很难满足实际需求,尤其是在目标探测起始阶段,多个动目标航迹起始信息判读、目标方位参数估计等均存在较大误差。多目标航迹起始是海上机动目标跟踪领域的首要问题。它是建立新目标档案的决策环节,本质上是一个决策问题[1]。对于多目标航迹处理,正确的航迹起始是减小航迹处理负担、提高机动目标跟踪质量的重要前提。由于目标一般是由远到近出现在探测传感器有效探测范围内的,在航迹起始时,目标一般距离探测传感器较远,此时传感器探测分辨力低,测量精度差,加之真假目标的出现,无真正的统计规律。因此,在多目标航迹处理中,航迹起始问题是一个难题,而杂波环境下的多目标航迹起始问题尤为困难。

针对传统的基于逻辑规则方法存在的问题,本文提出了一种在杂波环境下基于多假设思想的航迹起始算法。算法的思想是对相邻2个扫描周期的数据按启发式算法起始所有可能的假设航迹,然后在下一扫描周期将接收到的数据与假设航迹进行关联,采用S-D分配算法来求解关联的全局最优解,实现对真实航迹的确认,同时删除虚假航迹,并通过多源数据融合获取海上多个目标的方位信息,提高航迹数据估计精度,并能够对目标实施机动跟踪。

1 船舶雷达系统的信号模型

船舶雷达系统与海上机动目标的空间布局如图1所示,船舶雷达系统的总数为Ns,则方位坐标可记为si=[xi,yi,zi]T,i=1,2,…,Ns。令多个海上机动目标的初始方位坐标为xp=[xp,yp,zp]T,则各船舶雷达系统在t0时刻第i个站观测信号的到达时间(TOA)为:

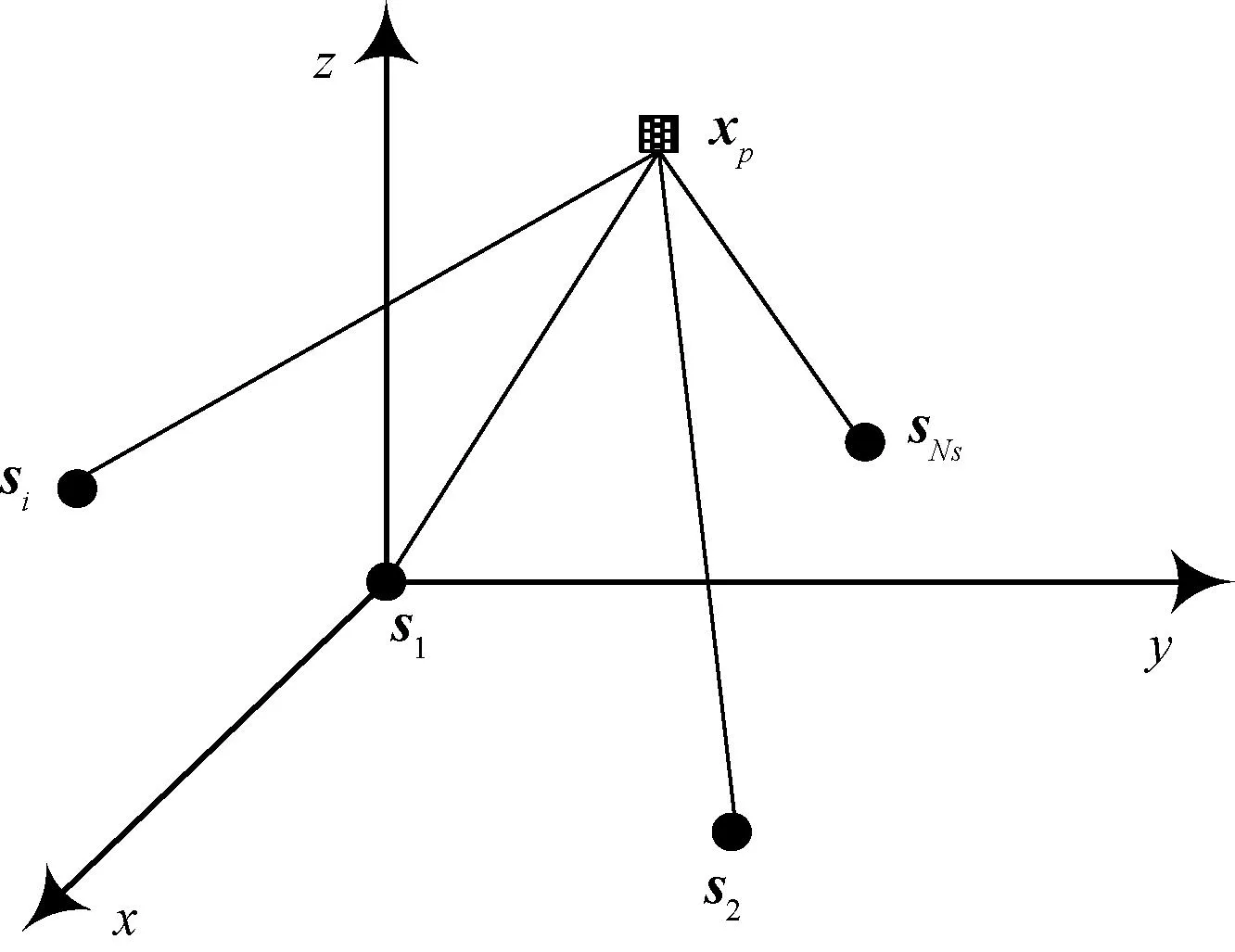
图1 船舶雷达系统与海上机动目标的空间示意图

ti=t0+‖si-xp‖/c+εi

(1)

式中:c为信号传播速度;εi为测时误差。

由于t0是未知的,可以利用两站的到达时间差构成量测消去t0,就可以得到1个用到达时间差(TDOA)表示的量测方程。令Δti,j=ti-tj,则:

Δti,j=(‖si-xp‖-‖sj-xp‖)/c+εij

(2)

式中:εij=εi-εj。

以第1个站作为参考(也可以其它站为参考),可以得到Ns-1个TDOA量测方程,将这些方程写成矩阵形式,可以表示为:

zk=h(xp)+nk

(3)

其中:

(4)

(5)

(6)

(7)

对于式(3)所描述的非线性方程,可以应用Chan方法求出目标的定位解。

2 基于量测-量测关联的广义S-D分配算法

各船舶雷达在任意时刻的位置都是确定的,但是基于该系统的多目标跟踪场景中,目标个数通常是未知的。

在“量测-量测”关联过程中,某一时刻第s个船舶雷达收到的TOA量测数据个数为ns,s=1,2,…,S0。第s个船舶雷达中的量测数据分别表示为zsis,is=0,1,2,…,ns,其中is=0为人为增加的虚拟量测,若将虚拟量测分配给某一目标,表示该目标没有被第s个船舶雷达检测到。

f(zsis)=1/ψs

(8)

式中:ψs是第s个船舶雷达观测区域的体积。

另外,假设虚警量测间统计独立,且独立于目标。

选择似然比作为代价函数ci1,i2,…,iS,即:

(9)

式中:Λ(Zi1,i2,…,iS|xp)表示S元量测Zi1,i2,…,iS源于第p个目标的似然函数;Λ(Zi1,i2,…,iS|p=φ)表示Zi1,i2,…,iS不是源于目标;由于Λ(Zi1,i2,…,iS|xp)中的xp是未知的,因此可以使用它的最大似然(ML)估计来代替[5],即:

(10)

假设不同传感器的量测噪声是不相关的,则源于目标p的S元测量Zi1,i2,…,iS的似然函数可以表示为:

Λ(Zi1,i2,…,iS|xp)=

(11)

式中:PDs表示第s个船舶雷达的检测概率;u(is)为二值指示性函数,定义为:

(12)

假设TOA量测噪声服从零均值高斯分布[6],则:

(13)

实际上,由于t0未知,上述方程无法计算。为此,以某个站作为参考站,用TDOA量测来代替TOA测量,从而将t0消除掉。选择S元量测中,某个非虚拟量测对应的雷达作为参考(为方便起见,这里以船舶雷达1作为参考),则时差量测zsis,1i1=zsis-z1i1服从高斯分布:

(14)

由于时差量测不满足不相关的要求,因此,在计算代价函数时,需要考虑时差量测之间相关的因素。

将S元量测中的S个TOA量测转换成(S-1)个TDOA量测,这(S-1)个TDOA量测服从联合高斯分布,即:

(15)

式中:zk=[z2i2-z1i1,z3i3-z1i1,…,zsis-z1i1]T;h(xp)和Rk表达式分别如式(6)和(7)所示。

另外,(S-1)元量测中可能包含有虚拟量测,此情况下,将zk中相应的列,以及Rk中相应的行和列删除即可。经上述变化后,式(11)的似然函数就可以由(S-1)元TDOA量测来表达:

Λ(Zi1,i2,…,iS|xp)=

(16)

若S元量测都是虚假量测或与该目标无关(用p=φ表示),其对应的似然函数为:

(17)

式中:ψs表示船舶雷达s的监视区域体积。

将式(16)和(17)代入式(9),可得代价函数:

(18)

多维分配算法的目的是寻找最有可能的S元量测集合,要求每个量测只分配给1个目标或虚警,而且每个目标至多收到来自各个列表的1个量测;至于虚拟量测,没有太大的限制,但要保证S元量测中的非虚拟量测能够对目标进行定位[7]。上述描述可以转化为如下的S-D分配问题:

约束条件为:

(19)

式中:ρi1,i2,…,iS是二值变量,用以表征量测组合Zi1,i2,…,iS是否与某个目标关联,若Zi1,i2,…,iS与某个候选目标关联,ρi1,i2,…,iS=1;否则ρi1,i2,…,iS=0。

通过引入虚拟量测,使关联能够在完整的S元量测上进行。对虚拟量测没有太多的限制,但每个S元量测中真实量测数不得小于1个最小值,以保证该S元量测能够对目标定位。由多个船舶雷达组成的雷达系统对三维空间目标进行定位,真实TOA量测数至少为4个。当S≥3,求所述多维分配问题的解是NP-hard问题,即求解的复杂度随问题规模的增大呈指数规律增长。

3 杂波环境下多目标航迹起始算法流程

算法如下:

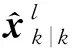
计算候选关联组合(l,Zm)的代价clm,若上述条件不满足,则令clm=0。若某个暂时航迹的跟踪门内,只有一个S元TOA量测,则直接将该量测分配给该航迹,并将两者从S-D分配算法中删除,以减小问题规模。

在杂波和虚警存在的情况下,可能会起始虚假航迹。但若杂波密度不大的情况下,虚假航迹存在的时间一般很短。

4 仿真验证与数据分析

为验证本文算法的有效性,采用船舶雷达系统对3个目标进行航迹起始的模拟。假设雷达系统由4个分站组成,在三维直角坐标系中的位置分别为:站1[0,0,20]T,站2[0,2.5×104]T,站3[-21 651,-12 500,15]T,站4[21 651,-12 500,25]T。采用时差量测体制,且各站的测时误差标准差为σt=10 ns,采样间隔T=1 s。整个监视区域为长7 km,宽7 km,高1.2 km区域。

图2中目标1和目标2做匀速直线运动,目标3以角速度π/360 rad/s在水平面内做匀速弧线运动;3个运动目标前20 s的轨迹如图2所示。每次扫描,雷达各分站的虚警数目服从参数为λ=10的泊松分布,且虚警在整个监视区域内服从均匀分布[10]。假设传感器的检测概率均为1。

图2 海上多个机动目标的运动轨迹

采用本文方法进行航迹起始与目标跟踪,在300次Monte Carlo仿真基础上,得到3个目标的航迹起始概率以及虚假航迹概率如表1所示。可见,该算法具有很高的航迹起始概率,以及较低的虚假航迹起始概率。一般只要连续3个周期都能扫描到海上机动目标,就能够为该目标起始航迹,具有很快的反应能力。

表1 目标的航迹起始概率及虚假航迹概率

采用匀速运动模型和扩展卡尔曼滤波器(EKF)对这3个目标进行跟踪,图3给出了基于300次Monte Carlo仿真得到的3个目标的均方根位置误差,可以看出采用EKF能够使跟踪误差迅速减小并收敛到稳定状态。

图3 目标1～3的位置均方根误差

从图3可以看出,该算法能够快速起始目标航迹,并完成机动目标位置的近实时精确估计,这对于船舶雷达系统要求有快速的航迹反应时间是非常有利的。

5 结束语

为了有效解决单船舶雷达目标探测与跟踪精度低、易误判等问题,本文结合杂波环境中的多目标航迹起始问题,提出了基于广义S-D分配算法的多目标航迹起始与机动跟踪算法,对相邻周期的量测按速度门准则形成暂时航迹,将下一时刻的量测数据与这些暂时航迹进行关联,以确认航迹,同时删除虚假航迹。通过仿真验证了该算法具有较高的精度和稳定性,具有一定的借鉴意义。