音律学数理思维在作曲中的应用研究

张杰文,薛亚东

(兰州职业技术学院 初等教育学院, 甘肃 兰州 730070)

一、音律与音律学简介

音律学是从发声体的振动规律出发,运用数学计算乐音体系音阶中各音的由来及精密高度,是物理声学、数学计算和音乐理论互相渗透的一门交叉学科。由于音律学与数学计算的重要关系,又称为数理音乐学[1]。作为音乐学的一个重要分支,“音律学在阐明律制的原理之外,还讲述律制在音乐各方面的应用。”[2]笔者以物理原理、数学模型和数列逻辑为基础,分析和弦、音律、节奏、序列音乐产生的原理和方法,从而指导人们的音乐创作实践,并运用这些分析方法更加深入地研究音乐结构、和声、音高、节奏等特性。

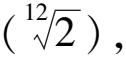
音律作为音乐最基本的物质基础,是产生音列、旋律、和声的理论基础和物理支撑。在音律学数理思维的基础上进行作曲实践,不仅能够帮助作曲家更好地理解音乐,还可以提供新的创作工具,使作曲技术变得更加多样化。例如,巴赫的《平均律钢琴曲集》是音律学理论在作曲技术方面应用的重要成果;以十二平均律为基础的有序列主义音乐,代表人物为奥地利作曲家勋伯格和他的学生威伯恩、贝尔格;运用周易六十四卦衍生乐曲的有太极作曲系统;以五行数理思维为基础的有五行作曲法;以十天干和十二地支为逻辑的有天干地支作曲法等。“音律学是实践性很强的学科。任何音律学学说,若脱离了音乐实践,将必然或对实践无益,或使自身受损。”[3]近年来,随着数字化的迅猛发展,音律学的重要性更加凸显了出来。在音乐软件中,作曲家不仅能够按照自己的创作意图设计任何一个乐音的音高,还能用音源将这种音响效果准确地展现出来,并根据调式来微调音高。由此看来,作曲实践也推动了音律学的数字化发展。

二、和声中的数理思维

和声的音响效果较之单声部音响具有更加丰富的表现力。在分析和生成和声的过程中运用数理方法,使原本复杂的和弦连接变得更加富于逻辑。和声音响构成的物理基础是泛音列,泛音列最初的几个分音结合为大三和弦。古希腊毕达哥拉斯的和声比例关系奠定了音乐中和声的数学基础,影响了西方的音乐理论和实践的发展。毕达哥拉斯通过观察和分析,发现当一根弦被分成整数比例的部分时,例如一根弦被分成一半、三分之一、四分之一等等,所产生的音调听起来会更和谐。这些整数比例的分割产生了基本和声关系。

(一)基频和驻波决定和弦色彩

音律学研究的是20～20,000 Hz这一频率区间内的声音以及它们之间的关系。乐音振动体的振动会产生一个基频和多个谐频,基频决定振动体的音调,而谐频则决定其音色。

1.依据根音基频和驻波判断和弦音色

物理学中,当两列振幅、频率相同的波迎面相遇,会在介质中形成看起来没有移动的波,称为驻波。满足基音的驻波并不只有一个,而是一系列等于有效弦长倍数的波列,波列对应的音频有高有低,人耳对低频更为敏感,因此一个音的频率越低,可辨识的泛音列越长。从这个角度来讲,处在和弦中最低的音最为重要。和弦的根音在不转位的情况下就处在最低位置,根音的“基频”决定了这个音上建立起来的和弦的音色。和根音产生的驻波越多,意味着这个音在和弦中决定音色的地位越高,所以和弦音中振幅、频率相同的音其驻波较为稳定,与自己的反射波相互增强,而其他波与反射波相互削弱,最后消失。根音或者转位之后的低音更容易产生低频驻波,使这个音显得尤为突出,在整个和弦中起了主导作用。

2.依据镜像设计和弦音色

镜像和弦是通过音符倒置排列,制造出一种类似于“回声”的效果,这也可以被称为“回文效应”(“回文”是指正读和倒读都一样的词语、句子或数字)。例如,将《闪烁的小星星》这首曲子的音符序列倒置,会发现它听起来就像是原旋律的回声。这是因为《闪烁的小星星》的音符序列是重复的,所以无论正序还是倒序播放,都会产生相同的效果(图1)。

图1 《闪烁的小星星》旋律示意图

除了《闪烁的小星星》之外,还有很多歌曲也具有这种“回文效应”,这些歌曲的音符序列通常包含重复或对称的元素,使得它们在倒置时仍然保持和谐。将旋律音叠加就可以变成对应的和弦,所以这里对旋律的倒置分析同样适用于和弦。传统和弦进行模式往往比较单调,缺乏新意,而通过镜像和弦与原始和弦的交替使用,就可以在音乐中创造情感对比,打破传统和弦进行模式,给人们带来新鲜感和探索感。从上例和弦的镜像倒置还可以发现,镜像和弦可能会将一个明亮的原始和弦带来的愉快情感变成一种阴暗或悲伤的效果,使音乐更加生动和有趣。所以,依据物理现象产生和变化和弦、旋律,可以增强音乐的戏剧性和张力,使听众更好地感受音乐中的情感起伏和对比,体验到更加丰富的情感变化。

(二)和声功能的数理模型演变

在物理分析和弦色彩的基础上,运用数学模型方法来分析和解释和声的连接,这种数理的结合使人们能够清晰地看出和声连接中人的审美变化。和声进行中经常使用和声功能圈、音级功能模型来分析,使原本复杂的和声有条理地展现出来。

1.传统和声的功能圈模型

在多声部音乐的进行中,使用纯律可以获得丰富的音响,使用五度相生律可以产生以Ⅰ、Ⅳ、Ⅴ级作为泛音基音的大三和弦,这三个和弦完全合乎泛音音准,在此基础上形成突出导音的倾向性功能和声(T、S、D),其中S功能是介于两者之间的过渡功能(图2)。

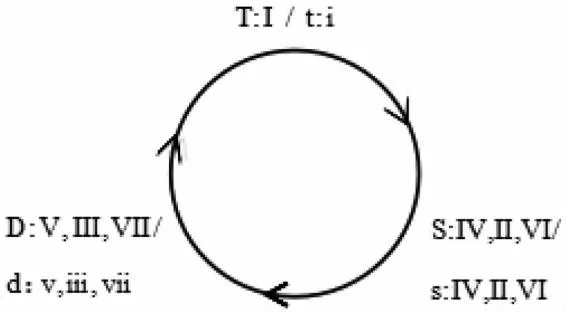
图2 传统和声的功能圈模型

2.现代和声音级功能模型

各个音级上产生的和弦都有自己的特性,这还是由低音谐频振动的原理决定的,每个音级在和声进行中都有它们各自的功能倾向。这种方法通常运用主音、属音、下行五度等描述和声的运动和关系(方框内功能区域内可以替换,图3)。

图3 现代和声音级功能模型

3.马尔科夫链模型

“马尔科夫矩阵”模型是通过“概率”分析和声连接的方法,使作曲者能够更加清晰地理解和描述和声的模式和转换,同时也为创作和解释音乐提供了一种数学工具。在当代音乐中,对功能和声的使用变得更加扩展和随意,尤其是许多当代流行音乐,和声进行出现了一种“套路化”的特征(图4)。

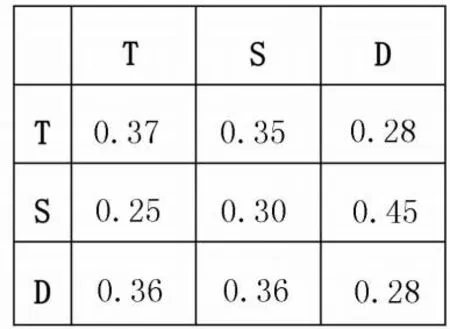
图4 马尔科夫链模型

从图4可以清晰地看出9种和声进行的状态,T(Ⅰ)连接到T(Ⅰ)的概率是37%,T(Ⅰ)连接到S(Ⅳ)的概率是35%,S(Ⅳ)连接到D(Ⅴ)的概率是45%。这个矩阵还可以随着选用和弦的增加而变化,每个音级上都可以产生一些不同的和弦,这个矩阵就会变得更大,使个性化创作的素材更加丰富。

(三)黄金标界和弦

古希腊的毕达哥拉斯学派认为,美感是由一些基本原则构成的,例如和谐、对称、比例等。植物的叶子、花朵和动物的身体均存在黄金分割比例。将这种比例关系运用到艺术作品中能产生最完美的和谐和美感。音乐家们将这种具有神奇魅力的数学比例关系运用到音乐创作中,创造出了“黄金标界和弦”。

“黄金标界和弦”遵循先创造音列然后由音列产生和弦的方法,将一条线段A分割为B、C两部分,B与A之比等于C,一条线段上有两个黄金分割点,分别叫做“顺点”和“逆点”。将A视为一首乐曲的全部,B、C点的交界处(也就是“黄金分割点”左右的乐句)常常被作曲家设计为乐曲的高潮。与黄金分割点相近的是“斐波那契数列”,这个数列的比例关系是从2∶3开始,然后用3∶(3+2),也就是3∶5;以此类推,就可以得出序列2∶3∶5∶8∶13∶21∶34∶55∶79∶134…经过笔者的运算,发现这种比例关系依次波浪式地接近0.618(见后文斐波那契数列表格)。为了完美乐曲的旋律也会起伏不断,然后达到高潮,这和斐波那契数列的递进关系如出一辙。

这些富有逻辑的数理结构,对于音乐的创作具有极大的应用价值,在音乐的序列编创中就可以借用某些数学推理的方法,创造出富有逻辑的音列来。只要在逻辑上有规可依,就可以创作出充满自然科学哲理的乐曲,这是人文哲学和自然科学结合的一种尝试。爱因斯坦、牛顿、钱学森等科学家常常用音乐来寻找科学的灵感,反过来,音乐家也可以在自然科学的研究成果中寻找音乐创作的思路,比如古老的la-so-mi三音列童谣的黄金标界原理(图5)。

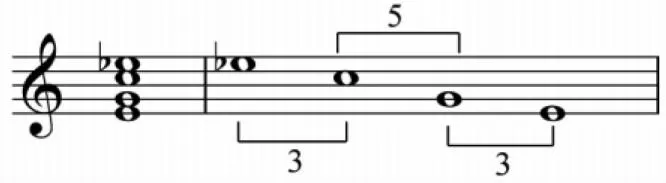
图5 黄金标界和弦

匈牙利作曲家巴托克·贝拉在音阶、和弦、节奏、结构等各个方面都有研究。巴托克的黄金标界原理的和弦,被称为“巴托克和弦”(图6)。

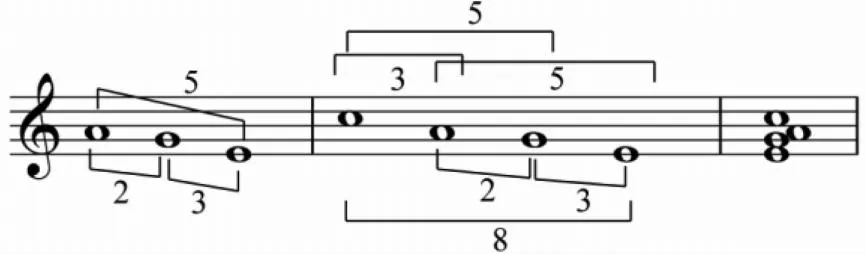
图6 巴托克和弦

伦德沃伊认为,从常见的一些和弦可以看到,它们之间的关系也符合黄金分割原理:全音阶和弦2+2+2+2,减七和弦3+3+3+3,四度和弦5+5+5+5,增三和弦之转位8+8+8(图7)。

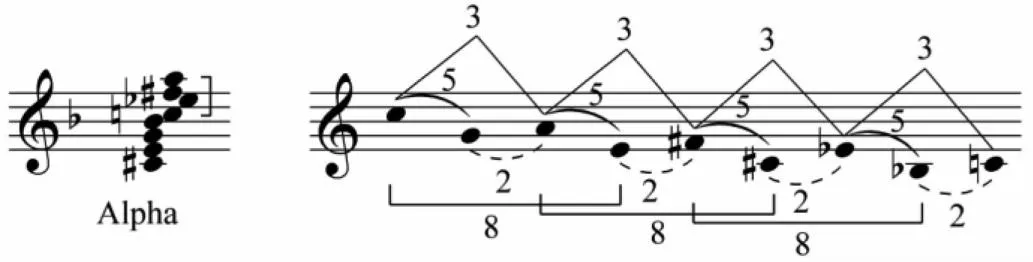
图7 几种和弦示意图

由此看来,数理思维的运用不仅强化了音乐分析的准确度,而且丰富了作曲技术,让作曲者在某种数理逻辑的指导下产生新的音列、和弦和结构。作曲技术要遵循自然科学的法则,和生活实践紧密结合,实现“源于自然,又超乎自然;艺术源于生活,又高于生活”[4]的艺术法则。这里借用数学中的黄金分割理论来建构和弦和音乐结构,从而将数理逻辑的美学意向演变成为一种作曲方法。

三、节奏的数理分析和应用

节奏是音乐的时间要素,从用数字来表示节奏、节拍、音符的时值,到运用数理思维来分析和生成复杂的节奏模式,节奏的创作和数理思维息息相关。通过数学方法可以研究节奏的结构和特点,创作出具有独特节奏感的音乐。

(一)用数字描述音符的特征

在音律分析中,人们常用罗马数字、阿拉伯数字表示音符的级数、音符名称等,唱名是根据奥尔夫音乐唱名法来规定的(图8)。

图8 音符名称对照表

正是因为这些数字标识的应用,人们建立了音符的各种逻辑关系。在音乐学习的时候,人就可以通过标记来发现乐曲内在的逻辑,可以通过数理分析得到新的创作方法。比如,序列标记中,就将C音作为开始音,用半音数来表示各音到第一个音的距离,音程数就为0,#C和bD是等音,音程数为1,依此类推,B音的序列号就是11。这种标记方法为序列音乐的创作打下了数理的基础,创作中就可以比较方便地使用。

(二)运用数理的变化规律衍生节奏

“二十世纪之后的许多作品则在摒弃了调性法则后,将全部的注意力集中于不同的音乐参数,在构建音乐事件的过程中所显现的形式化逻辑。”[5]节奏的结构力在序列的作用下得到解脱,从节奏的独特视角推进音乐,由新颖的节奏构思主导音乐结构,使音乐更有魅力。“12音序列作曲法”从产生到演变都可以从数理中找到其变化的规律,从节奏的设计中就可以找到现代音乐和调性时期音乐的区别(图9)。

图9 《钢琴的时值与力度的模式练习曲》(奥利维尔·梅西安)

从图9可以看出,三行乐谱从高到低分别使用的是三十二分音符、十六分音符、八分音符,它们的音值呈现出倍数递增的规律。第一行乐谱使用的三十二分音符,从1个到12个依次展开(中间次序出现调整),第二行乐谱使用的十六分音符,从1个到12个依次展开,第三行乐谱处于低音声部。作曲家更多地汲取了数理的思维方式衍生节奏型,“内在联系的数理因素在音像上有很强的感染力。”[6]

四、音列的数理特点分析和应用

音律学作为音乐理论中的一个重要领域,在研究音程、音色的基础上,研究音的排列和组合规律,依据音律衍生原理来设计音列,是乐曲创作的重要开端。

(一)用音律产生音列的逻辑

1.雅乐音列

《战国策》记载:“郢人作《阳春》《白雪》,其调引商刻羽,杂以清角流徵。”[7]看来古人的乐调音列是靠“引”“刻”“杂”来创造的。“引”的意思就是“起于”,它和中华雅乐调“起音毕曲”的“起”意思一样,由此判断《阳春》《白雪》的主音就是“Re”;“刻”就是深刻的意思,“A”是属音,有半终止的感觉,听觉自然深刻。“杂以”突出了作曲技法中经过音的使用,“夹杂”“混杂”的意思,可以像“辅助音”一样,用在“D”“A”的前面或者后面;“流”同样有经过的意思。当然古人的乐调音列的衍生和变化还有“清”,“清角”就是#F,“清角”是从哪个律制衍生而来的呢?就是逆宫而生;还有“变”,表示降低半音,比如“变宫”就是“B”。由于原曲早已失传,李健正先生选择了用音相同的曲调《北京的金山上》(图10)进行演示,以便让人们感受到这种曲风的味道。

图10 《北京的金山上》示例

从“引”“刻”“杂”“夹”“流”“变”“清”这些变音的方法可以看出上古先哲丰富的乐律创造手法。

2.黄金音列

依据以上分析,笔者设计了“黄金音列”。将十二平均律的12个音由低到高按照0～11的顺序依次排列,C音为0,#C音为1,依次按照半音数往上推,B音就是11。将斐波那契数列中大于音数12的值减去12n,确保音数在0～11之间,从而得出余数和余数音列。余数音列中到第八个音都没有重复,但是没有出现3、11、4序列的音,所以把这八个音命名为“黄金8音”。将12个音全部罗列出来,按照大小顺序,将F变为E,数值较大的11号F变为#F,数值最大的12号F变为#F,再将最后的F改为B,得出“黄金12音”(表1)。

表1 “黄金12音”统计表

由表1可以得出“黄金8音”(图11)和“黄金12音”(图12)。

图11 “黄金8音”示例

图12 “黄金12音”示例

(二)序列音乐中律制的相对固定和灵活运用

序列音乐的排列组合有三种方式:横向可移动性、纵向可移动性、纵横可移动性。这些序列可以是音高、力度序、时值序列,也可以是音色序、组织性序列等。序列音乐最早的序列是音高序列,后来发展到力度、时值序列等,又进一步扩展到色彩性的、组织性的序列,这样多维度的音乐语言更加具有表现力。那么,“序列音乐”会遵循哪种律制呢?

1.序列音乐中的律制

“有了律制应用的自觉性,就可将音律科学和音乐艺术的关系处理得恰如其分。”[8]传统音乐创作中,由于平均律在和声乐器中使用起来比较方便,易于转调,剔除了自然律复杂的音程变化,起到了中和、调节的作用,所以和声乐器的乐曲一般使用十二平均律。多声部音乐(这里指合唱和乐队)的创作中,十二律的和声纯度就不够用了,达不到和声的谐音效果,因此创作无转调、离调的无伴奏合唱曲或乐段时,就要以纯律为主将作者的意图准确、完美地表达出来,因为纯律中的大三度、小三度和转位后的音程,与人们听觉可以感受到的自然泛音列相吻合,构成协和度相当高的音响效果,给人以自然和谐的美感。

序列音乐中的律制主要采用十二平均律,每个半音的音高都是唯一的,而且相邻半音之间的音程是相等的。在序列音乐中律制的应用要注重音高和音程的准确比例关系,使序列音乐更符合音律的逻辑,产生更加丰富的音响效果。所以,在序列音乐的创作中也要融入纯律和五度律,在和声音乐、单旋律音乐中分别加以灵活运用,既不影响转调,又能增加音乐的美感。

2.运用现代测音技术控制音准

测量音的振动频率是音律学常用的一种方法。随着测音技术的进步,测量音高不再是一件难事,用测音软件测量音律既精确又便捷。无调性音乐要做到音律美,其音准很难控制,对“视唱练耳”教学来说也是很大的挑战。有时人们会在乐谱上通过标记律制和频率来说明音准,这种提示仅仅是文字性说明,不能解决根本性问题。为了使演唱(奏)的音准达到最准确的状态,最行之有效的方法还是在音准训练中用仪器测量音高,将音准的“观感”和“听感”相结合,最终达到音律美的效果。以下是“F”音三种律制的频率(图13)。

图13 “F”音三种律制的频率

图13是以“F音”为例,用手机APP测出的十二平均律、五度相生律、纯律三种律制的音高频率。

当然,音乐的风格多种多样,音律也是形态各异,测音软件可以根据要表达的音乐风格来设计音高。《律学》一书指出:“民族音乐的音律方面的研究,是民族音乐研究中重要的一环;利用现代先进的测音技术或自制的测音工具,对我国各民族的民族民间音乐或戏曲音乐等进行广泛的音律测算和律制核定。”[9]在民族音乐中,有很多特殊音律的要求,测音软件可以通过细微的调整来满足不同风格的需求。比如秦腔里的“中立音”“#F”“bB”,在软件中就可以自己设计它的音律。笔者将音频率做了临时调整(图14)。

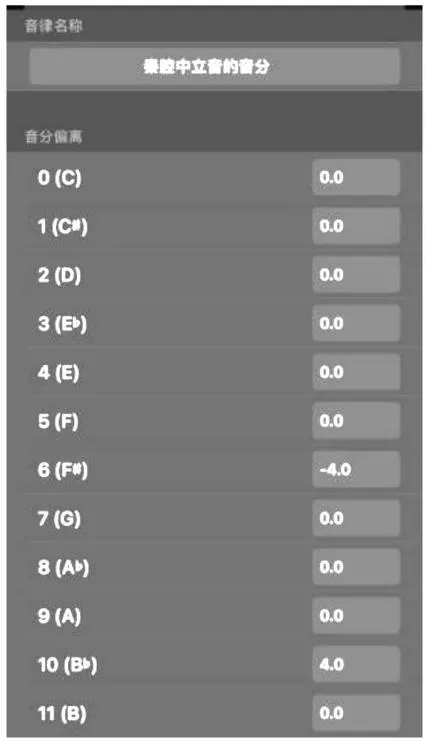
图14 运用“弹性律制”将音频率临时调整

这种细微的差别靠人耳是很难辨别的。在“视唱练耳”训练的时候,用测音软件进行不同律制的音准训练,将抽象的声音具体为音频数字,再由具体数字抽象为音高感觉,经过长期的视听训练,音准就能做到真正的音律美。

五、结语

正如爱因斯坦所说:“这个世界是由音乐的音符组成的,也是由数学公式组成的。音符加数学公式,就是真正完整的世界。”[10]笔者以音的物理特征为原点,在原理性研究的基础上,以数学逻辑推理为手段,研究了和声色彩、数理模型、节奏和音列的数理特点以及作曲中的构建方法,为作曲技术的发展和进步提供了新的视角。随着音律学数理思维的广泛应用,这种将原理性学习与创作性实践相结合的方法,将为学习者学好音乐打下良好的基础。通过观察音的物理属性,建立音列逻辑,再结合作曲软件平台、音律测试软件等工具,就可以降低作曲的难度。为此,音律学数理思维不仅可以在专业作曲中应用,还可以在以培养作曲兴趣为主的课程教学中加以应用,从而加强音乐基础教育中创作能力的培养。从这个意义上讲,音律学数理思维之于作曲的研究善莫大焉。