星载InSAR方位向逐行的顺轨有效基线计算方法❋

刘昆池, 苗洪利, 杨忠昊, 张佳辉

(中国海洋大学信息科学与工程学部, 山东 青岛 266100)

海流的研究对海军作战、海上救援、海岸带建设、渔业、船舶航运路线的制定、海洋环境的监测和预报等都有重要意义[1-2]。海流计[3]、浮标、地波雷达[4-5]等难以实现全球范围的观测,星载干涉合成孔径雷达(Interferometric synthetic aperture radar,InSAR)是一种微波遥感技术,具有全天时、全天候、数据处理精度高等优点[6]。InSAR分为单星重复轨道、单星双天线及双星编队伴飞等方式[7]。利用InSAR技术的顺轨干涉测量(Along track interferometry,ATI)可以进行地面运动目标的速度监测,当然也可应用于海洋领域,如海表面流速、海面风速、冰川运动及舰船速度等方面的观测[8-11]。ATI反演海表面流速相比于单景SAR多普勒中心偏移法(DCA)[12-13]具有更高的时空分辨率和反演精度。而顺轨干涉基线的准确估算在InSAR数据影像配准、平地相位去除[14]、地形相位计算等方面具有重要地位,是反演高精度海表面流场的关键参数[15]。目前,常用的方法是从卫星影像的头文件中直接读取或基于影像相位中心计算获得顺轨有效基线长度。在反演海流方面,使用单一值反演整幅影像对应的径向流速会有很大的误差。本文在进行轨道拟合计算基础上,建立顺轨有效基线值与方位向行号的函数关系式,得到方位向每一行的顺轨有效基线长度,以实现在海流反演方面的顺轨有效基线的精细化使用,将会带来反演精度的提高。

1 顺轨干涉有效基线及海流速度反演

InSAR测量中的基线是指两个天线对同一地面目标观测时,主辅天线相位中心(Antenna phase centre, APC)的连线,也称为物理基线[16]。如果是双发双收的模式,有效基线长度等于物理基线;如果是单发双收,有效基线长度为物理基线的一半[10]。有效基线在方位向上的投影为顺轨干涉有效基线,在距离向上的投影为交轨干涉有效基线。

ATI-SAR反演海流方法的基本原理为[8]:在两个天线均工作在条带模式下,在前后扫过海面上同一个区域时,后天线到达前天线照射的同一海面区域的时间差ΔT为:

(1)

式中:V为卫星平台的速度;Be为ATI的顺轨有效基线长度。当被前天线照射的区域再被后天线照射时径向(信号视线方向)移动的速度ULOS为:

(2)

式中:ΔR是前后两个天线通过被照射区域所接收到的信号的路程差。

对于单发双收模式:

(3)

式中:λ为信号波长;φATI为两个天线所接收到信号的相位差,正是ATI-SAR所要获得的两幅图像的干涉相位数据。

ULOS不但包括由风、浪等因素造成的海流径向速度,还包括长波轨道速度和Bragg波相速度,将ULOS径向速度做地距投影之后,再去除后两项速度才能得到海流的距离向速度。

ATI-SAR获取两幅图像的时间差应该充分长,以便得到可靠的相位差,但同时也要比后向散射区域的去相干时间短[17]。海面后向散射区域的去相干时间τcorr可以近似表达为:

(4)

式中σorb为重力波轨道速度的标准差,可近似为σorb=0.068U10,其中U10是距离海面10 m高度处的风速[18]。假设风速大小为6～12 m/s,信号波长为0.031 m,则海面后向散射区域的去相干时间为4.3～8.6 ms。

2 顺轨有效基线计算方法

顺轨有效基线的计算需要轨道方程的确定、图像对偏移量的获取、基线矢量的投影及有效基线方程的建立四个步骤。

2.1 轨道方程的确定

卫星轨道如图1所示意,由于轨道数据时间分辨率较高,采用多项式拟合,确定卫星位置方程和卫星速度方程[19]。

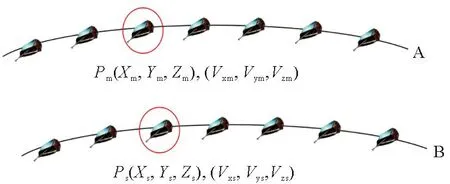
图1 卫星飞行轨道示意图Fig.1 Schematic diagram of satellite flight orbit

在图1中,A和B分别表示主辅卫星对应的轨道,从卫星数据头文件可知,每个卫星提供了时间间隔为1 s 的轨道参数,包括在WGS-84坐标系下的空间位置和飞行速度。例如Pm为轨道A(主卫星)的某一点,其空间直角坐标为(Xm,Ym,Zm),在三个坐标轴上飞行速度为(Vxm,Vym,Vzm),Ps为轨道B(辅卫星)的某一点,其空间直角坐标为(Xs,Ys,Zs),其飞行速度为(Vxs,Vys,Vzs),用一段时间内的主辅轨道参数进行拟合,采用三次多项式,以时间为自变量:

(5)

(6)

式中:(X,Y,Z)、(Vx,Vy,Vz)为卫星的位置和飞行速度;ai,bi,ci,di,ei,fi为多项式系数(i=0,1,2,3)。

2.2 图像间偏移量的获取

在InSAR图像中方位向第n行的成像时刻t(n)为:

(7)

式中:PRF为脉冲重复频率;t0是成像起始时刻。由于主辅卫星有各自的轨道方程(5)和方程(6),而原始的主辅图像可能存在同一行号像元对应的不是同一地面成像点,因此,在使用辅卫星轨道方程时,使用的行号n需要和主卫星的行号配准。

解决主辅图像行号的统一问题,首先需要进行图像对偏移量的确定。具体方法为,选取主卫星图像的场景中心为控制点,利用相干系数作为匹配测度对辅卫星图像的偏移量进行确定。相干系数γ的计算公式为:

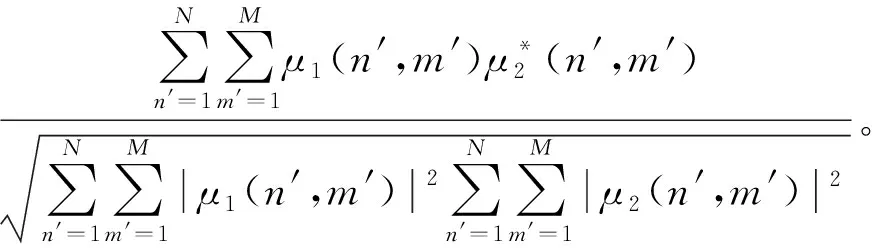
(8)

式中:N和M为计算相干性的图像块尺寸大小;n′和m′为数据块内行列号;μ1(n′,m′),μ2(n′,m′)为主辅影像数据块内影像坐标(n′,m′)处的复数值;|·|2为数据的二阶范数。

确定偏移量分为像元级和亚像元级。像元级偏移量是在主图像中以控制点为中心选取一个匹配窗口,再在辅图像中选取一个相对较大的搜索窗口,在搜索窗中遍历匹配窗口,分别计算各自的相干系数,以相干系数最大的遍历位置确定图像像元偏移量,即中心像元位置差,以此决定要调整辅图像的行号数。

ATI-SAR成像间隔是毫秒量级,在此期间海面随机运动导致后天线记录的海浪纹理相比于前天线已经产生了一定的变化,图像间海浪纹理的相关性会急剧下降[20],因此在利用相关系数法获取图像间偏移量时,所选区的匹配窗口应包含陆地区域,以减小偏移量计算的误差。

为提高顺轨有效基线计算精度,还可以进一步计算亚像元级偏移量。首先对匹配窗口和搜索窗口进行过采样,采用sinc函数插值的方法,插值间隔取0.1个像元。用同样的遍历方法可以确定亚像元级偏移量,此时主辅图像统一后的行号变为小数级。

2.3 基线矢量的投影

顺轨有效基线几何示意如图2所示。

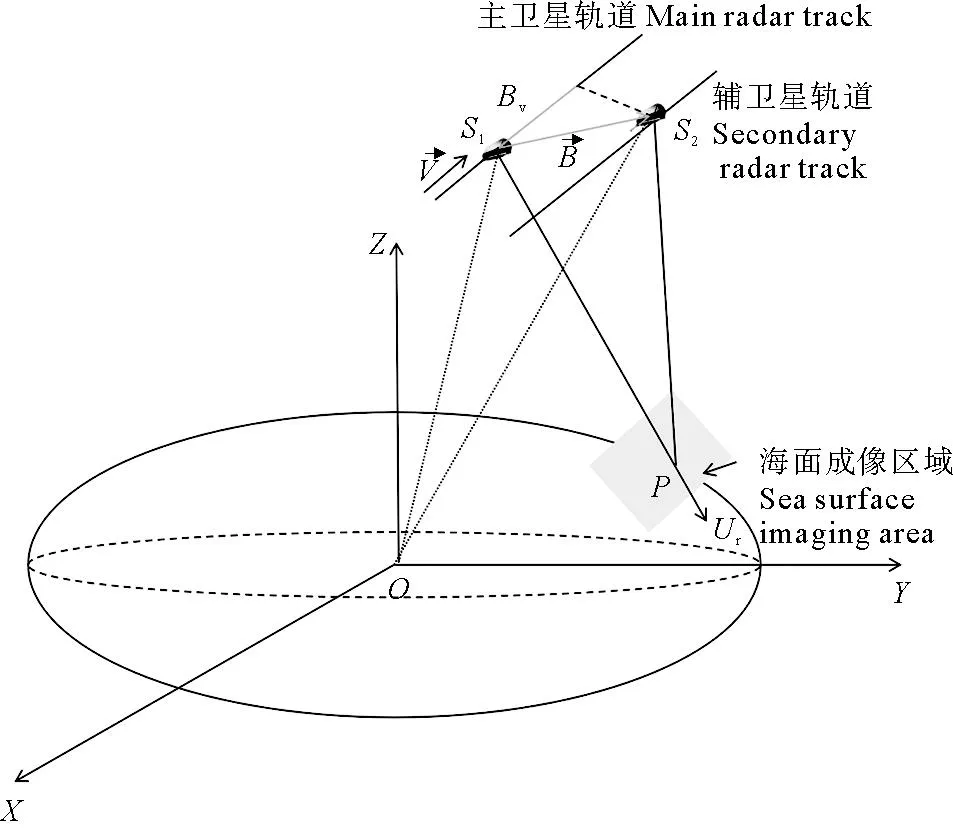
图2 有效基线几何示意图Fig.2 Schematic diagram of effective baseline geometry

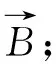
(9)

当只有一个天线用于发射,两个天线都用于接收时,顺轨有效基线Be是顺轨物理基线的一半。

2.4 有效基线方程的建立

目前常用的方法是将成像区域中心行对应的两星位置及时刻和卫星速度等信息获得中心行对应的有效基线,并将该基线值应用于整个刈幅。然而,卫星按照轨道运行时,由于各方面的原因导致卫星姿态不稳定,对方位向各行像素点成像时两个卫星之间并不是一个固定的基线值,使得获取同一对干涉影像时顺轨有效基线的长度是一个随方位向上行号的变量。

为了解决上述问题,需建立顺轨有效基线与方位向上行号之间的关系式,以便获得每一行的顺轨有效基线值。

通过式(5)、(6)、(9)可推导出针对单发双收模式顺轨有效基线Be与成像行号的函数关系为:

(10)

式中tm和ts分别为主卫星和辅卫星对同一目标点成像的时刻,即:

tm=[(n-1)/PRF]+tm0。

(11)

ts=[(n-1)/PRF]+ts0。

(12)

其中tm0为主图像第一行成像时间,ts0为辅图像与主图像配准后的第一行成像时间。

3 应用结果分析

将以上有效基线的计算方法应用于TanDEM-X/TerraSAR-X卫星,时间为2012年3月19日6:41,地点为奥尼克群岛地区。主图像的大小为20 782×18 432,即行号从1到20 782。选取从2012年3月19日6:41:15—6:41:32时间段,采用三次多项式拟合主卫星位置方程和速度方程分别为式(13)和式(14):

(13)

(14)

辅卫星的位置方程为式(15):

(15)

使用相干系数法获得方位向平均偏移量为0.141,把午夜零时设定为0 s,则主卫星成像起始时刻为24 079.843 0,辅卫星成像起始时刻为24 079.838 8。将行号(1—20782)逐个通过式(7)获得所在行对应的主辅卫星成像的各自时刻,再通过轨道方程(13)、(14)、(15)获得主辅卫星的瞬时位置和主卫星瞬时速度。通过公式(10)即可得到对应各行的有效基线Be。结果如图3(a)所示。

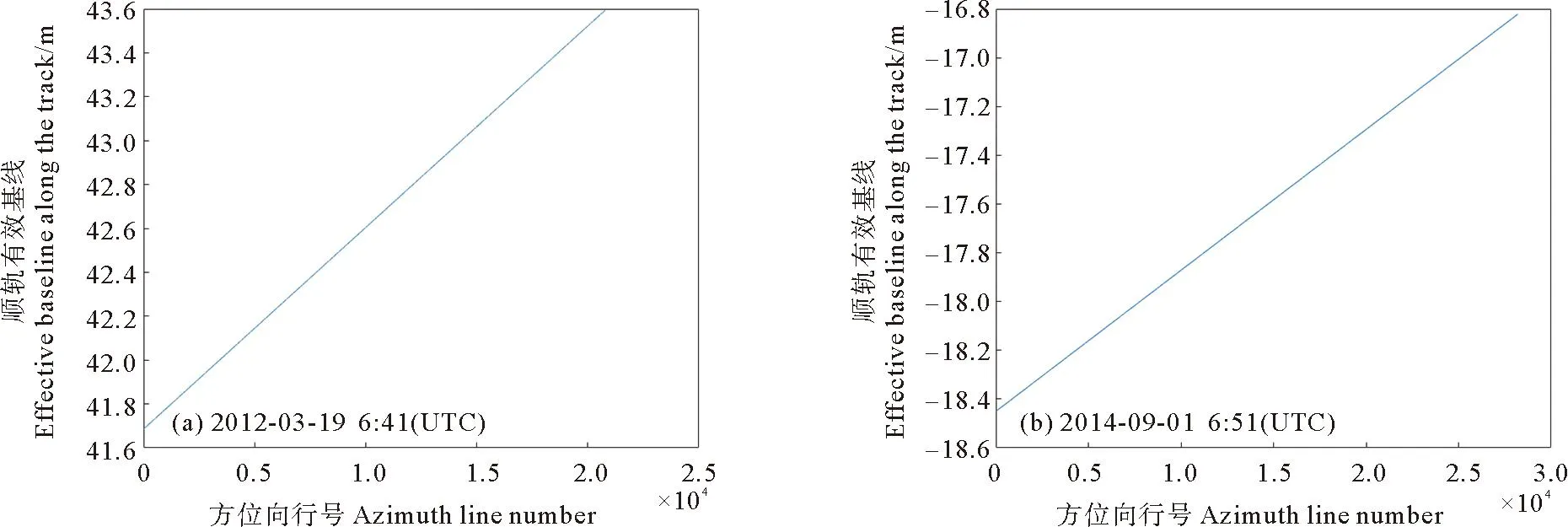
图3 顺轨有效基线与方位向行号关系图Fig.3 The relationship between the effective baseline along the track and the azimuth line number

针对TanDEM-X/TerraSAR-X卫星获取的另一对顺轨干涉数据(时间:2014年9月1日6:51,位置:苏格兰西南的艾莱岛附近),主图像的大小为:28 200×12 790。利用同样方法获得的顺轨有效基线与主影像方位向行号关系如图3(b)所示。

从图3(a)可以看出,在整幅图像上,顺轨有效基线从41.7～43.6 m,变化范围约1.9 m。从另一对数据的结果(见图3(b))看,顺轨有效基线的变化范围也同样接近2 m。而通过传统方法计算的只是中心行对应的顺轨有效基线,两对干涉数据的顺轨有效基线分别为42.6和-17.7 m,与参考文献[10]所述顺轨有效基线大小接近。由于卫星轨道高度距地都有几百公里以上,无论是交轨干涉还是顺轨干涉,干涉结果对基线长度的变化十分敏感,将以上固定值应用于整幅图像无疑会带来较大误差。

从图3(a)和3(b)还可看出,Be与图像方位向行号呈线性变化,这不是必然结果,可能是由于两卫星在该幅图像成像期间,其姿态稳定,始终保持了平行。针对这样的结果,在后期应用时,可以使用拟合的线性方程来替代公式(10)的繁琐计算。两对干涉数据的顺轨有效基线与行号的简易线性方程如式(16)和式(17)所示:

Be=41.685 7+9.184 7×10-5n,

(16)

Be=-18.449 8+5.776 9×10-5n。

(17)

通过TanDEM-X/TerraSAR-X卫星实测数据(时间:2012年3月19日6:41时,位置:奥尼克群岛地区)进行海面流速估计,以判断逐行顺轨有效基线对海面流场精度的影响。逐行使用不同的顺轨有效基线,海流流速反演结果如图4所示。

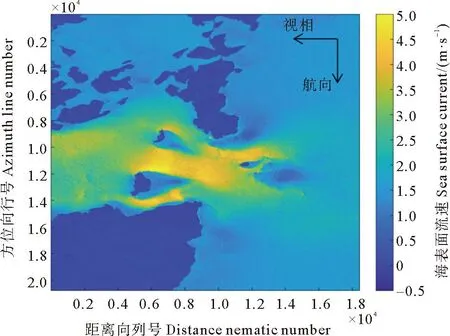
图4 奥尼克群岛地区海流流速反演图Fig.4 Inversion map of ocean current velocity in the Onik Islands area

分别使用传统基线计算方法和改进的基线计算方法进行海流流速反演,计算两幅图像方位向上每一行的流速均值,其结果如图5(a)所示,在方位向上每一行的海流流速差值如图5(b)所示。由图5(b)可知,在方位向上逐行使用不同的顺轨有效基线值能够一定程度提高海表面流速反演精度。

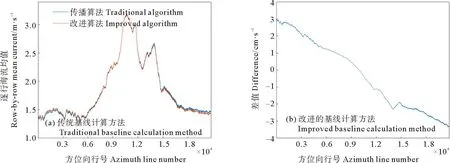
图5 两种算法流速反演结果对比Fig.5 Comparison of flow velocity inversion results between the two algorithms

4 结语

本文通过轨道方程的确定、图像对偏移量的获取、基线矢量的投影及有效基线方程的建立四个步骤完成顺轨有效基线与方位向行号的函数关系式的建立,用以在主辅图像干涉时顺轨有效基线的精细化应用是对传统计算方法的改进,有效避免在整幅图像上使用固定基线带来的误差。通过TanDEM-X/TerraSAR-X实测干涉数据对所述改进方法进行了应用和检验,同时针对所使用干涉图像对的特殊线性关系建立了快捷方便的线性方程,避免了繁琐的计算,更有利于提高程序化运行效率。通过在整幅图像上精细化使用顺轨有效基线会对诸如海流反演方面有效提高反演精度。