梳状高度计编队探测海洋涡旋仿真分析❋

王 绚, 马纯永,2❋❋, 梁 达, 赵朝方,2, 陈 戈,2

(1.中国海洋大学信息科学与工程学部, 山东 青岛 266100;2.青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室, 山东 青岛 266237)

在全球海洋中普遍存在一种空间尺度为数十至数百公里、时间尺度为数周至数月的旋涡,称为海洋涡旋[1]。按照极性不同可分为气旋涡(Cyclone eddy, CE)和反气旋涡(Anticyclone eddy, AE)两种。海洋涡旋动能占海洋动能的90%,主导着上层海洋流场。海洋涡旋在其核心内部可产生垂向运动,引起水团、热量、盐分等显著变化,促进海表和海面以下物质和能量交换,进而影响海域环流结构、大面积水团分布和海洋生物等,对区域乃至全球气候具有调节作用[2-4]。因此,对海洋涡旋进行观测、追踪与分析至关重要。

星下点高度计(Nadir altimetry, NA)可提供沿轨一维散点化海平面高度(Sea surface height, SSH)采样数据,空间分辨率约为50 km[5],这为海洋涡旋的探测提供了契机。星下点高度计可通过多源卫星融合的方式实现数据同化合并[6-8],形成网格化测高数据[9]。学者们对海洋涡旋探测及分析的研究兴趣日益增加,在全球多个海域开展相关实验。Kubryakov等使用1992—2011年高度计数据在黑海地区进行涡旋识别[10],Qin等利用1993—2010年海平面异常(Sea level anomaly, SLA)数据在中国东海开展中尺度涡流探测,对其极性、寿命、半径等属性进行分析,并揭示其季节、年际变化特征[11],Cui等在孟加拉湾基于22 a的SLA数据分析涡旋在该海域的活动情况[12]。众多研究证实,基于高度计数据进行涡旋识别探测具有可行性。但若网格化数据空间分辨率较低,会导致真实涡旋密度极大地被低估[13-14]。由单颗变为多颗星下点高度计编队联合观测,测高能力会随之提升[15],从而改善涡旋探测效果。但由于轨道设计、所在纬度和海域以及测高精度不同等原因,提升效果会存在差异[16]。近年来,联合观测生产的全球海面高度卫星测高数据集,推动了海洋学和其他地球科学的研究进程[17]。

随着海洋探测的进一步深入,宽刈幅干涉成像高度计(Wide-swath altimetry, WSA)应运而生[18],此高度计可生成沿轨数百千米尺度的宽刈幅观测条带。旨在将测高精度提升至厘米级别[19],并对垂直方向上的海洋运动进行直接观测[5],但其技术要求和研制所需经费比星下点高度计要高出数个层级,现阶段难以普及。由美国NASA与法国宇航中心合作研发,预计于2022年发射的地表水和海洋地形任务(Surface water and ocean topography mission,SWOT)卫星,将搭载Ka波段雷达干涉仪[20],实现数十米量级的空间分辨率和厘米级的垂直观测精度[21]。Ma等模拟SWOT采样并分析了测高误差对涡旋探测的影响[22],发现单颗SWOT卫星难以全面探测小尺度涡旋。中国青岛海洋科学与技术试点国家实验室提出的“观澜号”海洋科学卫星也是未来将要推进的科学探测任务[5]。在这一高度计发展的重大阶段,开展本研究的必要性和重要性不言而喻。

本文以黑潮延伸体海域(Kuroshio extension, KE)作为研究区域,采用5颗间隔均匀的星下点高度计卫星,组建梳状高度计编队(Comb altimeter constellation, CAC)。以单颗星下点高度计及宽刈幅成像高度计作为对比研究对象,定量化分析不同高度计卫星设计方案的涡旋探测能力差异。首先,分别对三种卫星设计方案进行采样仿真,得到该海域全年SSH采样数据。其次,经最优化插值算法(Optimal interpolation, OI)[23]处理后合成逐天SLA数据场,采用基于SLA数据场的混合涡旋探测方法进行涡旋识别。最后,基于涡旋数量、极性、半径、振幅等参数,对梳状高度计编队及其与单颗星下点高度计和成像高度计的涡旋探测能力差异进行定量化分析。

1 数据

1.1 HYCOM模式数据

近年来随着数据计算能力的大幅提高,高分辨率涡旋解析和海洋环流模拟研究已经在全球范围内开展。由多机构合作开发的混合坐标海洋模型(Hybrid coordinate ocean model, HYCOM)覆盖全球所有海域,其在涡流解析、实时全球预报和未来海洋预测等方面发挥了积极作用,并扩展了区域内海洋探测的可能性[24]。HYCOM数据在海洋盐度[25]、温度、动能[26]等多项研究中被广泛使用,其可用性已被实践证明。该海洋模型可以很好地代表中尺度变化,并为评估多高度计任务的测高能力提供了独特机会[27]。

西北太平洋黑潮延伸体(KE)海域(24°N—44°N,140°E—180°)涡旋能量丰富[28],是全球海洋涡旋研究的热点区域之一[29-30]。HYCOM高分辨率数据使我们得以从KE海域0.08°数值模拟数据中量化高度计任务时空采样映射后的SSH场质量,分析合并多卫星高度计任务对海平面高度测量的贡献。本文使用2015年HYCOM的SSH数据,并将其视作真实海面高度数据,即真值数据。其经纬度网格间距为0.08°,在KE海域,经度跨度所含网格点数为500个,纬度跨度所含网格点数为250个,图1绘制了单天HYCOM模式下的SSH空间分布图。分别沿星下点和成像高度计轨迹对KE海域进行SSH采样,并将相应测高误差添加其中。有关采样仿真的详细设计将在2.1节进行详细介绍。

图1 HYCOM海平面高度(SSH)数据Fig.1 HYCOM SSH data

1.2 高度计卫星轨道设计

目前传统高度计能探测到直径超过100 km的中尺度海洋涡旋特征[31],但由于观测误差和采样空间分辨率的限制,它们不能解决亚中尺度(半径在10～50 km)的涡旋特征。为尽可能减少轨道设计对后续数据插值和涡旋识别的影响,本文以中国自主设计的观澜卫星轨道为采样基础,对梳状高度计编队、单颗星下点高度计和成像高度计的测高能力及涡旋探测能力差异进行探讨。

观澜卫星轨道为太阳同步轨道,轨道高度989 km,重访周期16 d,轨道数206条(见表1)。本文使用5颗相同的星下点高度计卫星,在跨轨方向上间隔100 s呈现队列式飞行,来实现梳状高度计编队近乎瞬时的多星沿轨采样,其中每个星下点高度计又可单独工作,对海表面进行独立观测。为降低轨道间隔对后续网格化数据场插值的影响,以观澜成像高度计卫星的刈幅宽度(180 km)为参考,本文设计的5条轨道跨轨宽度大致与成像高度计刈幅宽度相吻合。为便于理解,图2绘制了不同高度计模式沿轨采样示意图。图中NA1-NA5为5颗星下点高度计,黄色长方形区域对应成像高度计,箭头方向为卫星运行方向,即沿轨方向。NA1-NA5星下点高度计依次排列,共同组成梳状高度计编队,均匀分布成像高度计所跨刈幅区域内。其中,NA3为单颗星下点高度计模式,位于梳状高度计编队和成像高度计采样轨道的中心位置。

表1 观澜卫星的主要参数Table 1 Main parameters of Guanlan satellite

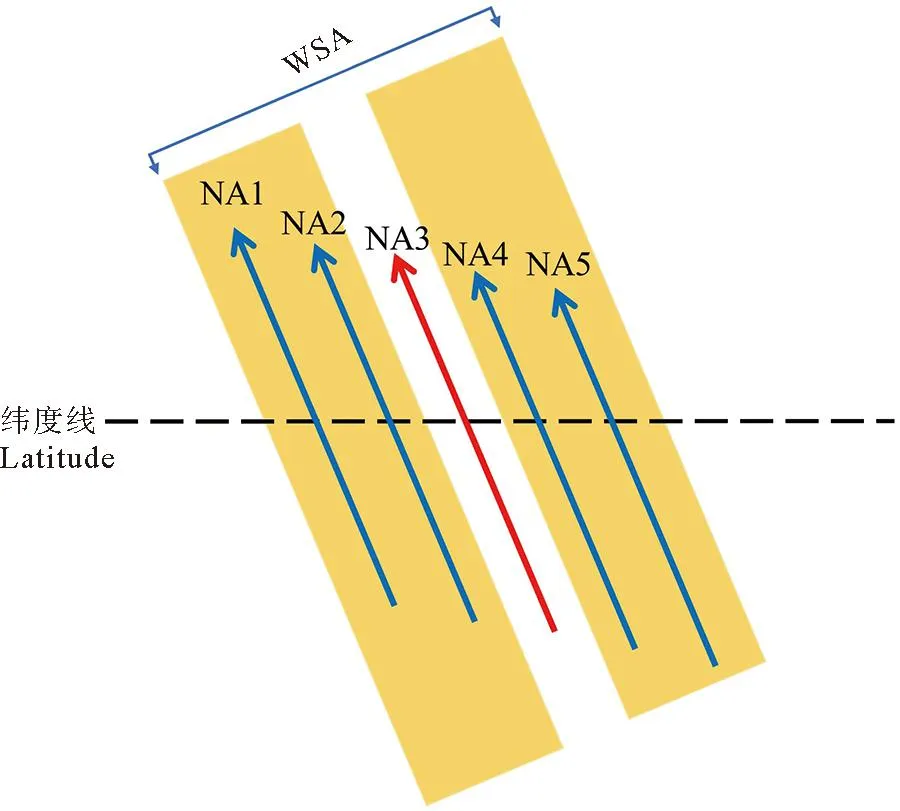
图2 高度计卫星设计示意图Fig.2 The schematic diagram of altimeter satellite design

少于数天时间间隔的卫星采样环境误差将在两条平行轨道间高度相关,因此大部分环境误差可被消除。但轨道误差是随机的,无法通过系统性处理较好地去除。因此,本研究假设轨道误差在可控范围内不予考虑,仅将每一轨对应的SSH采样误差考虑在内。

2 研究方法

本文基于不同高度计卫星方案SSH采样仿真数据,经数据优化插值后得到网格化SLA数据场,使用混合涡旋识别方法进行涡旋识别探测。不同高度计逐天SLA网格化数据场,是沿各自轨道方案基于0.08°分辨率HYCOM数据采样后的单天SSH数据,去除全年平均SSH值,经OI插值处理后得到的。

2.1 高度计SSH数据采样仿真

本研究假设轨道误差在可控范围内不予考虑,仅将SSH采样误差考虑在内。高度计任务测高精度的提升需要一系列非常精确地验证和校准作支撑。目前使用地面站、GNSS浮标、验潮仪和星星交叉等校准方法,星下点高度计SSH偏差普遍降到几毫米至几厘米的水平[32]。Ma等发现,成像高度计观测误差会影响亚中尺度及中尺度涡旋特征观测[22]。故在高度计采样数据中,我们在每轨星下点高度计采样中添加了2 cm左右的误差,并在成像高度计沿轨及跨轨方向上添加了2～3 cm左右的误差,以模拟真实的采样输出情况。

对于采样仿真而言,全球轨道采样数据是多余的。因此,我们只关注所选取区域内的轨道。最终得到KE海域内全年测高观测数据,每条数据中包含沿轨坐标(经纬度)、SSH、采样误差等信息。星下点高度计沿轨生成一维散点测高数据,成像高度计在沿轨和跨轨刈幅宽度上生成二维网格化测高数据。本文设定的成像高度计采样空间分辨率为5 km,总刈幅宽度为180 km,中间空白区域宽度为30 km,有效刈幅宽度为180 km-30 km=150 km,可提供高空间分辨率的SSH数据,能够覆盖大部分中尺度海洋现象,为海洋学研究提供观测数据。

图3绘制了一个重访周期内的SSH采样图,图3(a)为单颗星下点高度计采样结果图,图3(b)为梳状高度计编队采样结果图,图3(c)为宽刈幅成像高度计采样结果图。可以看出单颗星下点高度计采样空间分辨率较低,轨道间交错形成的“菱形”区域面积较大,插值处理后其中心误差值较大,这将对后续的涡旋识别造成影响。而梳状高度计编队通过5条间隔均匀的轨道联合观测,其“菱形”面积远远小于单颗星下点卫星,沿轨采样可实现高时空分辨率。我们可以从梳状高度计编队采样图中较直观地看出KE海域的SSH变化趋势。虽然星下点高度计仅提供沿轨一维散点采样,但在梳状星下点高度计卫星编队方案下,其与成像高度计采样效果十分接近。

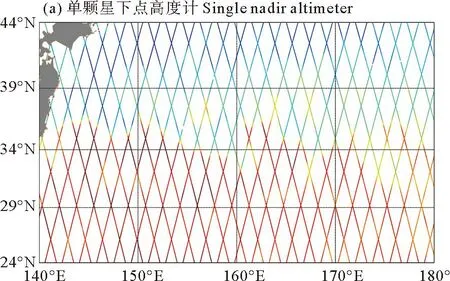
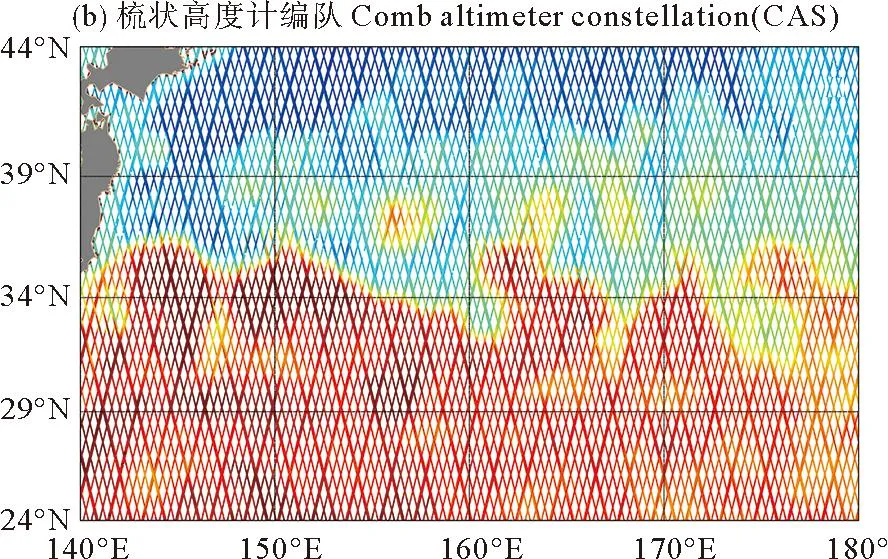
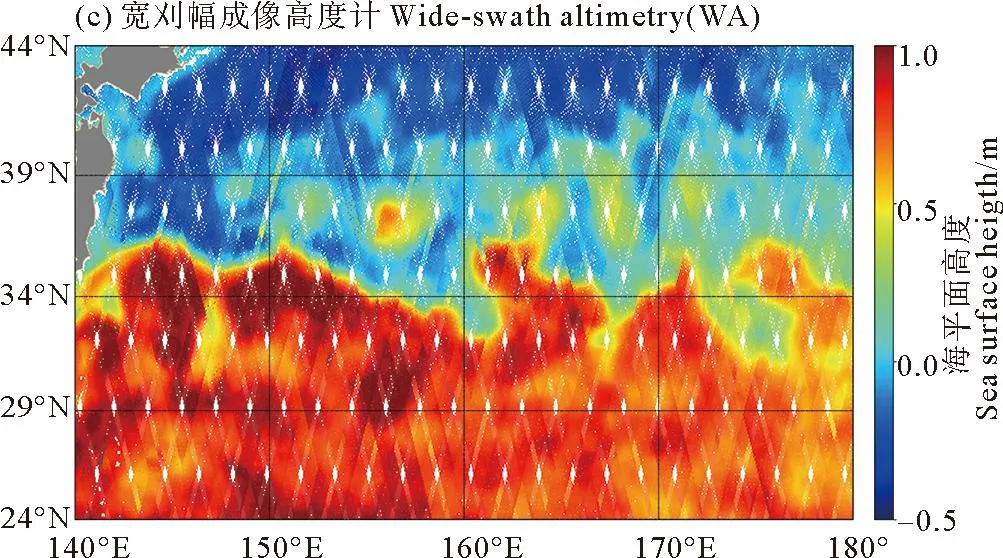
图3 不同高度计卫星方案海平面高度(SSH)采样图Fig.3 SSH sampling map of different altimeter satellite schemes

2.2 沿轨采样数据插值优化及技术

考虑到采样仿真得到的SSH数据空间采样间隔大致相同(数千米),但时间间隔(数分)远小于HYCOM海面真实数据(数天)。我们并没有对采样后SSH数据进行实时沿轨网格化插值,而是逐天将一个重访周期(16 d)内的轨道数据重新划分并合并完成采样数据集重构。更具体地说,去除全年平均海平面高度场数据(Mean sea surface height, MSSH)后得到的逐天SLA数据,经最优化插值方法(OI)处理,在KE海域背景场基础上,将一个重访周期内SLA数据融合为一天的网格化SLA数据场,卫星采样数据被重构为整数天。由此,得到后续涡旋探测方法所需的逐天SLA数据场。计算公式如下:

SLA=SSH-MSSH。

(1)

其中,插值后数据场也呈现“菱形”分布,最大值出现在轨道交叉形成的“菱形”中心。由于梳状高度计编队提高了轨道密度,因此尽可能减少“菱形”区域面积,也就减少了误差在空间上的变异性。

本文使用的数据集重构算法是在客观分析法基础上发展而来的的优化插值技术,是目前最常用的数据重构算法之一。对三种高度计方案模拟采样后的数据集使用同样的OI插值映射方法,由沿轨数据重建二维SLA数据场,将重建后的SLA数据场与HYCOM处理后的SLA数据场相减做差进行对比,以量化海平面高度映射数据过程中的误差情况。将梳状高度计编队、单颗星下点高度计和成像高度计采样数据OI插值后的SLA数据场,分别与HYCOM数据所得的SLA数据场做差进行误差对比分析,并且对全年时间跨度内SLA数据场误差数据进行平均,其均值、标准差情况在表2中详细列出。SLA数据场的质量评定中,梳状高度计编队和成像高度计误差情况相近,其全年平均标准差分别为6.94和6.84 cm。而单颗星下点高度计全年平均标准差约9.49 cm,与上述两种卫星设计方案的差距较大。

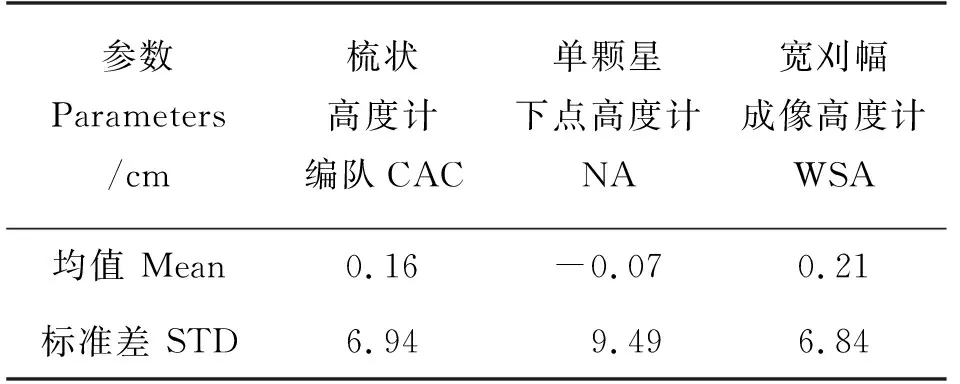
表2 全年SLA数据场的误差情况Table 2 Error of SLA data field in the whole year

2.3 基于SLA数据场的涡旋探测算法

检测和表征中尺度涡流是一项重要的研究工作,在KE区域,我们使用Mason等基于测高数据网格化产品的自动涡旋检测算法[33],定量研究了一年时间跨度内空间分辨率为0.08°的逐日SLA数据场变化情况,对区域内涡旋进行识别探测。简单来说,首先,对SLA数据场进行空间高通滤波。其次,提取SLA数据场局部极值。最后,绘制SLA闭合等值线,在最值区域搜索闭合SLA等值线,完成涡旋识别。在计算机计算能力允许的情况下,该识别算法支持并行处理,可提升涡旋识别效率。当然,基于SLA数据场对涡旋进行识别检测的过程中也会出现误检和小涡旋漏检的情况,Liu等对该算法进行了优化和提升[34],但这并不是本文讨论的重点。

基于SLA数据场的涡旋探测算法,最终得到4个涡旋识别数据集,即HYCOM真值涡旋数据集(SLA method Eddy Datasets of Truth, SED_t)、梳状高度计编队数据集(SLA method Eddy Datasets of CAC, SED_c)、单颗星下点高度计数据集(SLA method Eddy Datasets of NA, SED_n)和成像高度计涡旋数据集(SLA method Eddy Datasets of WSA, SED_w)。其中,我们将HYCOM海洋模式数据视作真值数据集。

在图4中,我们展示了一天时间跨度OI插值后4个数据集SLA数据场的空间分布情况,SLA数值范围为(-0.4,0.4),单位为m。可以看出,SED_t、SED_c和SED_w三个数据集的SLA数据场空间分布情况类似,均在35°N纬度线附近出现大规模SLA正负数值交错的海平面高度异常特征,这表明这三种数据集对海平面异常的仿真模拟情况基本一致。但SED_n数据集在此区域内没有出现以上特征,却显现出类似卫星海面采样轨道线的“菱形”结构,这也就是我们前文所提到的“菱形”误差结构。

图4 OI插值后4个数据集海平面高度异常图Fig.4 Four sea level anomaly data after OI

3 涡旋探测定量化分析

3.1 涡旋空间分布可视化

本文在表3中对4个基于SLA涡旋探测算法得到的涡旋数据集的涡旋数量及极性进行了统计。由表3可知,SED_t、SED_c和SED_w 3个涡旋数据集的涡旋数量总体相当,分别为37 439、38 423和39 649个,SED_c和SED_w分别与真值数据集相差984(2.63%)、2 210(5.90%)。并且,在3个涡旋数据集中,相比于气旋涡,反气旋涡的数量相对较多。其中,SED_t、SED_c和SED_w中反气旋涡和气旋涡占比分别相差3.24%、4.16%和3.28%。而SED_n数据集总涡旋数量达到49 782个,比SED_t真值数据集高出约33%,其中反气旋涡多于气旋涡17%以上。SED_n中多出的33%涡旋数有很大一部分是由测高误差而被误检的涡旋和不存在的虚假涡旋所贡献的。相比于SED_c和SED_w数据集,其与SED_t真值数据集的重合度较低。在涡旋数量上SED_c与SED_t更为接近。而从气旋涡和反气旋涡占比来看,SED_w数据集与SED_t更相近。

表3 各涡旋数据集涡旋数量Table 3 Number of eddies in each dataset

将KE区域重新划分为1°×1°的经纬度网格,共计800个网格点。以涡旋质心所在经纬度点作为网格参考点,计算每个网格点中对应的涡旋数量。4个数据集中各涡旋数量分段等级所对应的网格点数统计情况如图5所示,由左至右依次为SED_t、SED_c、SED_n和SED_w数据集,单个网格点内涡旋数量分为0～25、25～50、50～75、75～100以及大于100个这5个等级。由图5可知,SED_t、SED_c、SED_w 3个数据集涡旋数量等级的网格数量分布总体特征相似,而在SED_n数据集中75～100以及大于100这两个等级的网格数量明显大于其他3个数据集,且在特定区域网格内集中出现,表明SED_n数据集所识别出的涡旋数量总量较大,且出现原本不存在的涡旋被错误检出的情况。

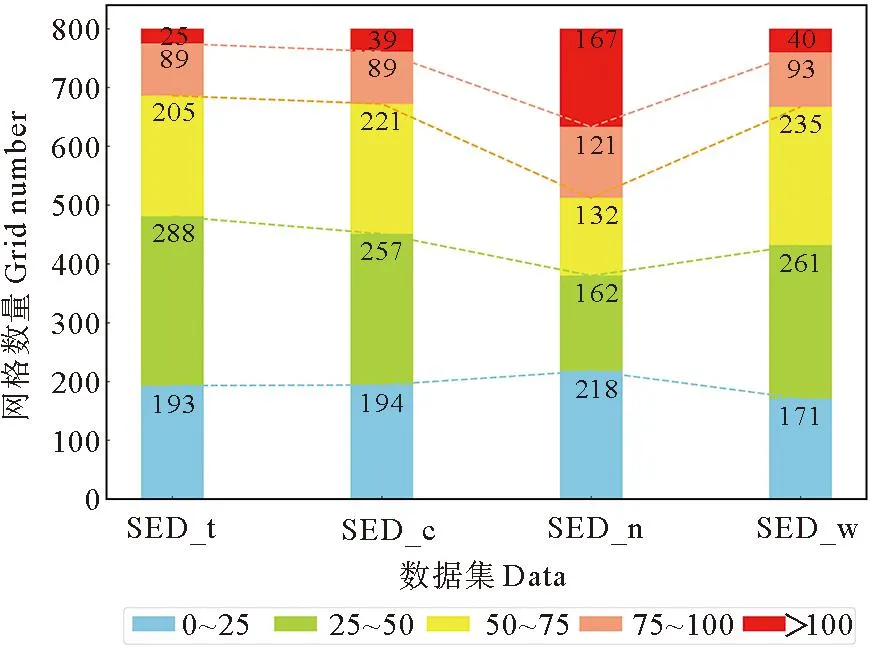
图5 涡旋数量网格分段统计图Fig.5 Grid statistics of eddy number

3.2 涡旋特征定量化分析

SED_t、SED_c、SED_n和SED_w 4个数据集中,涡旋平均半径分别为82.27、81.14、67.95和79.86 km。半径大于100 km的涡旋数量分别为11 426、11 280、8 451和11 337个,占总涡旋数的30.52%、29.36%、16.97%和28.59%,这表明SED_n识别出了较多小涡旋。同样以1°×1°尺度划分网格,以涡旋质心所在经纬度点为网格参考点,计算各网格点上总的涡旋半径及振幅大小,并除以该点对应涡旋数量,得到图6涡旋半径及振幅密度分布图。图中左侧为涡旋半径密度图,单位为km,右侧为涡旋振幅密度图,单位为cm。由图6可知,SED_t、SED_c、SED_w 3个数据集的涡旋半径密度分布总体特征相似,均在35°N附近出现半径密度的最大值,其网格点内单个涡旋平均半径可达100 km以上,这表明该纬度线附近的涡旋活动范围较大,水团运动剧烈。而SED_n数据集涡旋数量较大,涡旋半径普遍较小,网格点内涡旋半径密度值较低。此外,因边缘网格识别涡旋时,周围可供参考的SLA数据较少,可识别的涡旋数量较少,4个数据集最外圈网格的涡旋平均半径数值普遍偏低。

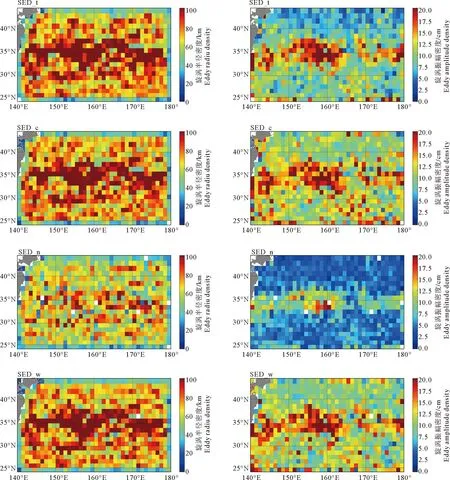
图6 识别后数据集涡旋半径及振幅密度分布图Fig.6 Eddy radius and amplitude density of the different identified dataset

涡旋振幅密度图中SED_n数据集总体数值仍然偏小,与其他3个数据集有很大差异。但不同于涡旋半径密度图中SED_t、SED_c和SED_w 3个数据集中较高程度吻合的情况,在涡旋振幅密度分布图中可以较为明显的看出SED_t和SED_c、SED_w数据集的高数值区域仍然出现在35°N附近,但在40°N以北地区出现了略微差异。在40°N以北地区,SED_t数据集所识别的网格化涡旋平均振幅数值整体偏低,表明SED_t识别出的涡旋振幅变化较小,而SED_c和SED_w数据集中的涡旋振幅总体上高于SED_t数据集。

此外,我们在图7中统计了涡旋数量随半径和振幅的变化情况。可以看出,4个数据集中涡旋数量随半径的变化趋势大体一致,先随涡旋半径迅速增大再缓慢减小,其中,SED_c和SED_w与SED_t分布情况更为接近,而SED_n涡旋总量最多,峰值明显高于其他3个数据集。SED_c与SED_t分布情况最为接近。总体上,4个数据集内大部分的涡旋半径小于150 km,在40～50 km的涡旋数量最多。并且4个数据集都没有探测到10 km以下的涡旋,半径超过300 km的涡旋也几乎不存在,而涡旋数量随振幅的变化情况有所不同,4个数据集总体均呈现下降态势,涡旋振幅主要集中在20 cm以下,而振幅大于50 cm的涡旋几乎不存在,其中SED_c、SED_w与SED_t变化情况更为接近,而SED_n变化幅度较为剧烈,特别是在振幅低值区间的涡旋数量明显高于其他3个数据集。SED_c和SED_w数据集各振幅区间的数量变化斜率较小,分布较为分散,两者变化曲线更为重叠,但与SED_t数据集变化情况存在一定差异,这也与图6所得的结论相呼应。

图7 涡旋数量随半径及振幅变化图Fig.7 The number of eddy varies with the radius and amplitude

3.3 涡旋匹配能力分析

涡旋识别完成后,我们得到SED_t、SED_c、SED_n和SED_w 4个涡旋数据集。在3.1和3.2节中,我们对其数量、半径及振幅等识别结果进行了相应分析。本小节中,我们将SED_t数据集视作真值,在此基础上,依据涡心位置、涡旋类型和涡旋边界等参数,将识别后的SED_n、SED_w涡旋数据集分别与SED_c数据集构建匹配关系,以评估SED_c数据集的涡旋匹配能力。也就是说,我们分别对SED_t、SED_c、SED_n和SED_t、SED_c、SED_w数据集进行涡旋匹配能力分析,以分别评价梳状高度计编队与单颗星下点高度计、成像高度计的涡旋探测能力差异。一方面,我们将数据集内涡旋性质相同,涡心位置相近的涡旋定义为“Match Eddy”,即配成功涡旋。但只有在极少数情况下,它们的涡旋边界能够完全重叠。其中,SED_t数据集中的单个涡旋可能在其他数据集中以分裂后的多个涡旋形态存在,也有可能SED_t数据集中的多个小涡旋在其他数据集中以合并后的单一涡旋形态存在,我们将以上这些情况均视作“Match Eddy”。另一方面,SED_t与其他涡旋数据集中互相没有匹配到参数相近的涡旋,则将各自数据集中相应的涡旋视为“Miss Eddy”,即匹配失败涡旋。其中,即使SED_n或SED_w与SED_c数据集中涡旋参数可相互匹配,但无法与SED_t匹配,我们也将SED_n与SED_w数据集中涡旋视作“Miss Eddy”。

图8绘制了一天内的涡旋匹配情况,以直观展示涡旋匹配结果。图中左侧为SED_t、SED_c和SED_n匹配情况图,右侧为SED_t、SED_c和SED_w匹配情况图。其中黑色代表SED_t,红色代表SED_c,绿色代表SED_n,蓝色代表SED_w。从图8的全部涡旋图中可以看到,40°N以北地区的总涡旋数量较多,且半径较小。而在35°N附近,海洋活动剧烈,涡旋半径普遍较大,并且SED_n涡旋总量明显偏多,并识别出较多小涡旋。这都与我们在3.1和3.2小节中的结论相符合。而从匹配成功涡旋图中可以看出,左侧图中,SED_t中单个涡旋在SED_n中被识别为多个涡旋的现象多于右图。如黑色虚线框中的涡旋,SED_t与SED_c、SED_w(黑线、红线和蓝线)的涡旋匹配结果都极为吻合,而在SED_n(绿线)中则被识别为3个单独的涡旋。此外,从匹配失败涡旋图中可以看出,左侧SED_t、SED_c和SED_n的匹配失败涡旋数量明显比右侧SED_t、SED_c和SED_w多,且大多为SED_n数据集中的小涡旋所贡献。如紫色虚线框中,SED_t、SED_c和SED_w数据集在这一海域中均以大涡旋形态出现,右图框中,基本没有出现涡旋匹配失败的情况,但SED_n数据集中却有众多小涡旋出现在左图框中,这表示SED_n数据集出现了较为严重的误检情况,将本不存在的涡旋识别出来,也就是说,其所代表的单颗星下点高度计设计方案不能较好地反映真实涡旋分布及形态。

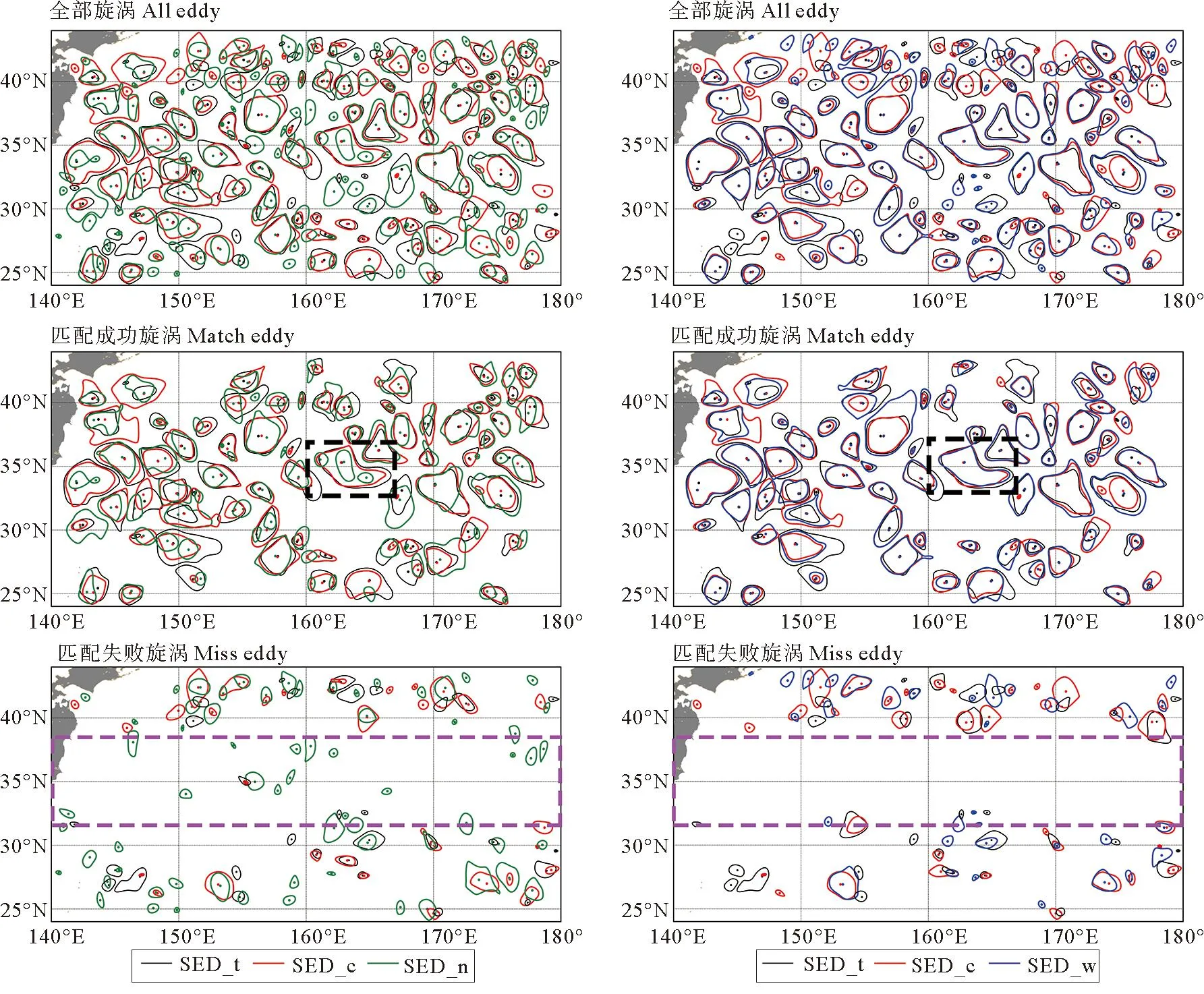
图8 涡旋匹配情况图Fig.8 Eddy matching diagram

表4和5中列出了当天涡旋匹配的详细数值,可以看出SED_t、SED_c和SED_n进行涡旋匹配时,匹配成功数量虽然略高于SED_t、SED_c和SED_w的匹配结果,但SED_n数据集的匹配失败数量(60+)远高于其他数据集的匹配失败数(30+)。基于上述对图8的分析,造成该现象的原因主要是SED_n数据集出现了误检情况,识别出较多不存在的虚假涡旋。反观表5中SED_t、SED_c和SED_w数据集的匹配情况,三者则具有较好的一致性。

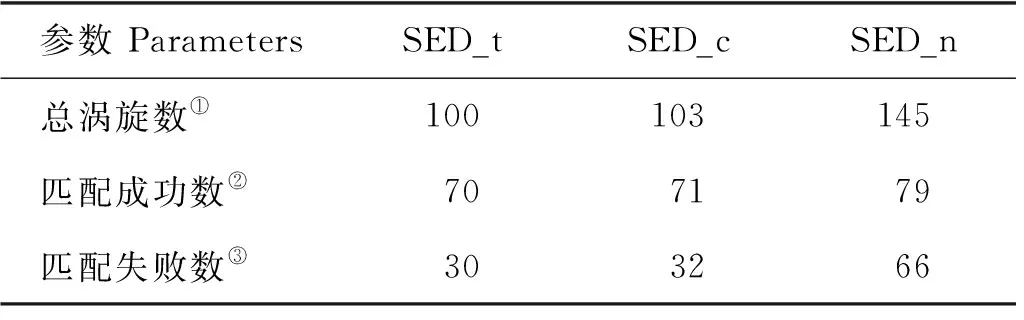
表4 SED_t、SED_c和SED_n涡旋匹配情况表Table 4 SED_t, SED_c and SED_n eddy match

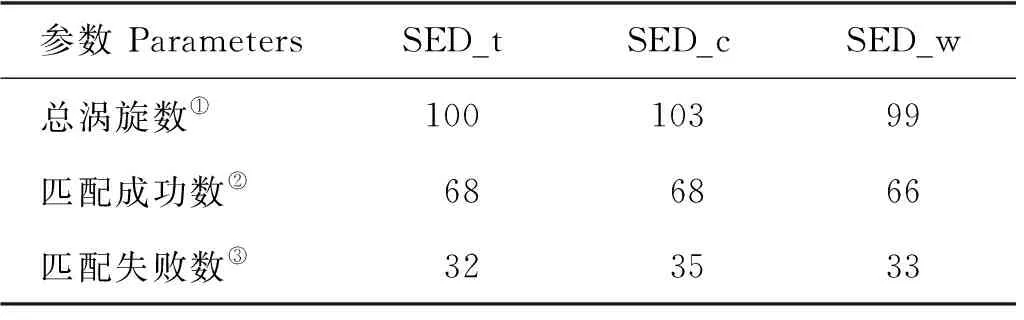
表5 SED_t、SED_c和SED_w涡旋匹配情况表Table 5 SED_t, SED_c and SED_w eddy match

为了进一步探究涡旋匹配特征,表6和7统计了全年范围内涡旋匹配的结果,其中括号内为匹配成功数所占总涡旋数的百分比。表6中各数据集的涡旋匹配成功率总体低于表7。由表6可知,SED_t、SED_c和SED_n涡旋匹配成功率约为55%,这主要是由于有一部分涡旋被误检,出现了一些虚假涡旋导致的。表7中,SED_t、SED_c和SED_w 3个数据集的全年涡旋匹配成功率约为62%至67%,匹配成功率总体相差不大。相比而言,涡旋识别后SED_c数据集的涡旋具有较高的匹配成功率,总体优于SED_w数据集。

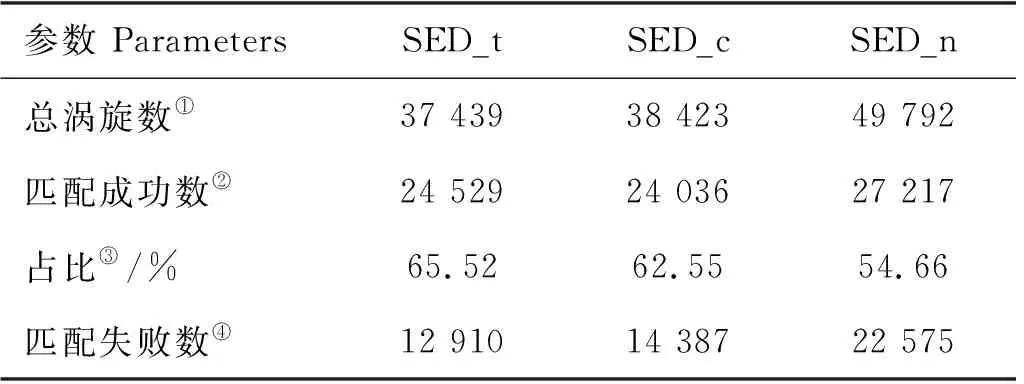
表6 全年SED_t、SED_c和SED_n涡旋匹配情况表Table 6 Annual SED_t, SED_c and SED_n eddy match

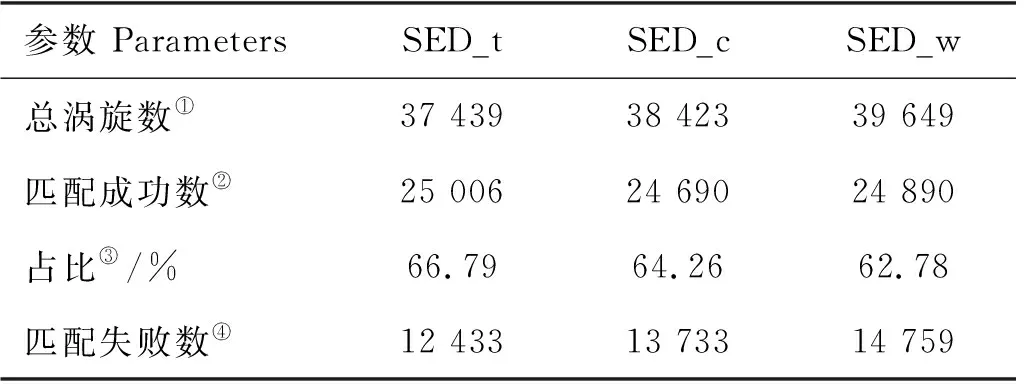
表7 全年SED_t、SED_c和SED_w涡旋匹配情况表Table 7 Annual SED_t, SED_c and SED_w eddy match

4 结论

本文设计梳状高度计编队方案,将HYCOM数据视作真值,进行全年含误差的SSH数据采样模拟,经优化插值算法处理后,再利用基于SLA的涡旋探测方法得到涡旋数据集,最后,将其与单颗星下点高度计和成像高度计卫星轨道设计方案所得的涡旋数据集进行对比分析。实验结果表明:

(1)梳状高度计编队方案测高及涡旋探测能力与真值数据集接近。梳状高度计编队识别出的涡旋数量与真值数据集相差984个(约2.61%),其涡旋平均半径约为81.14 km,与真值数据集相差1.13 km。在两种涡旋匹配方案中,梳状高度计编队与真值数据集涡旋匹配成功率分别为62.55%和64.26%。

(2)梳状高度计编队所代表的涡旋数据集在涡旋数量、极性、半径及振幅等方面与成像高度计涡旋数据集相近,涡旋匹配成功率约为62.78%。

总的来说,梳状高度计编队在对海洋涡旋进行识别探测和匹配方面,各项参数的统计结果较好,与成像高度计结果类似。相较成像高度计,其各项技术流程已相对完备和成熟,研制经费也远远小于成像高度计。因此,梳状高度计编队是探测涡旋的有益方案,并具有较强的可行性。