初中数学解题中待定系数法的应用策略

沈超雄

(福建省莆田市秀屿区实验中学, 福建 莆田 351100)

待定系数法作为初中数学中重要的解题方法,是一种“执果索因”的思维方式,是判断所求结果的结构形式,根据题目条件列出待定系数的等式,得出待定系数的值.待定系数法的应用比较广泛,在初中数学解题训练中,教师围绕待定系数法安排专题训练,指导学生用于多项式除法、因式分解、解方程以及恒等式的证明等多方面的试题,帮助其学会借助待定系数法有效解答初中数学问题,不断提高他们的解题能力,为将来的中考做好充足准备[1].

1 用待定系数法解多项式除法问题

在初中数学解题教学中,应用待定系数法能解答多项式除法类试题,包括多项式的余式、求商式和整除等[2].多项式除法属于除法的一种,在运算过程中还要用到减法与乘法,是代数试题中一类比较常用的算法,通常是用一个同次或者低次的多项式去除另一个多项式.教师可指导学生应用待定系数法解答多项式除法问题,让他们将一个相对复杂的除法问题分解成小问题,顺利解题[3].

例1 求(3x3-2x2+1)÷(3x2-3x+1)的商式和余式.

分析此题中被除式的最高次项是3x3,除式的最高次项是3x2,所以商式的最高次数是1,且系数是1.因此,可以将商式设为x+a,余式设为px+q,由此能够得出关于x的恒等式3x3-2x2+1=(x+a)(3x2-3x+1)+px+q,对于一切实数x均成立,所以,x为0、1、-1依然成立,从而得出关于a、p、q的方程组.

详解设所求的商式是x+a,余式是px+q,由此得到3x3-2x2+1=(x+a)(3x2-3x+1)+px+q,

令x=0,则a+q=1;令x=1,则(a+1)+p+q=2;

令x=-1,则7(a-1)-p+q=-4;

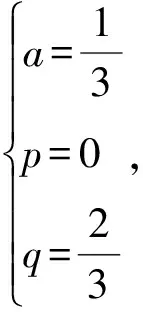
例2 已知x4+4x3+6px2+4qx+r可以被被x3+3x2+9x+3整除,那么p、q、r的值分别是什么?

分析在解此题时,需要先把商式假设出来,根据x4÷x3=x可以把商式假设成x+m,故p、q、r、m都是待定系数,结合被除式恒等于商式乘以除式,以及对应系数的对比,能求得这几个待定系数的值.

详解设所得商式是x+m,所以x4+4x3+6px2+4qx+r=(x+m)(x3+3x2+9x+3)=x4+(3+m)x3+(9+3m)x2+(3+9m)x+3m,

2 利用待定系数法解因式分解问题

对初中数学解题教学来说,当因式分解中遇到一些较为复杂的二元二次多项式时,应把原多项式中的一部分进行因式分解,且转变成两个一次因式相乘的形式,就可以把整个解题过程处理的简单化.对此,初中数学教师在因式分解类试题教学中,由于二元二次多项式比较复杂,当要求学生进行因式分解时,可借助待定系数法将原多项式的一部分进行因式分解,由两个一次因式乘积代替,使其在分解中确定因式,将解题过程变得更加简捷.

例3 已知2x2+xy-y2-kx+8y-15可以分解为两个一次因式的乘积,那么这个有理多项式是什么?

分析在解题时,可以将前三项进行分解,通过两个一次因式相乘的方式来表示,再对原式进行变形,就能够采取对应项系数比较的方式求得结果.

详解根据十字相乘法可以得到2x2+xy-y2=(2x-y)(x+y),设2x2+xy-y2-kx+8y-15=(2x-y+m)(x+y+n)=2x2+xy-y2+(2n+m)x+(m-n)y+mn.

例4 已知等式p2+q2=7pq,且满足该等式的正实数p、q,能够让有关x、y的多项式xy+px+qy+1分解为两个一次因式之积,请问p、q的值分别是什么?

分析根据条件p2+q2=7pq,且p、q是正实数,利用配方法分析p+q和pq的关系,因多项式xy+px+qy+1可以分解成两个一次因式之积,便可借助待定系数法把pq的值给求出来,并得到p+q的值,顺利确定p、q的值.

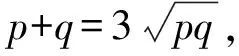
3 利用待定系数法解高次方程问题

方程,作为学生从小学时期就接触和学习的一类知识,在整个数学课程体系中占据着极为关键的地位,既是一类特殊的理论知识,也是学生进行解题的一种常用工具,重要性不言而喻.不过对于初中学生而言,还没有学习到有关高次方程的解题方法,当遇到此类特殊的方程类试题时,教师可以指引他们采用待定系数法,找到这些一元高次方程中根存在的某种关系,从而将高次方程转变为低次方程,使其能够借助待定系数法的优势顺畅解这类方程.

例5 已知方程2x4-5x3-24x2+53x-20=0的两个根之积为2,那么该方程的解是什么?

分析通过分析方程根和系数之间的关系,发现两根之积是2的一元二次方程,假如二次项系数是1,则常数项为2,故应用待定系数法时能够搭配假设法完成求解.

详解设2x4-5x3-24x2+53x-20=(x2+ax+2)(2x2+bx-10)=2x4+(2a+b)x3+(ab-6)x2+(-10a+2b)x-20,

例6 已知方程x4+(x-4)4=626,求该方程的实数解.

分析解答本道题目时,可以利用待定系数法,推导出方程的两个实数根,然后继续利用待定系数法进行因式分解,最终完成解题.

详解因为626=54+14,能够看出5和-1是该方程的两个根,令x4+(x-4)4-626=2(x+1)(x-5)(x2+px+q),当x=0时,q=37,当x=4时,p=-4,所以原方程可以变为2(x+1)(x-5)(x2-4x+37)=0,又因为(x2-4x+37)=0没有实数根,所以原方程的解是x1=-1,x2=5.

4 应用待定系数法解代数式恒等变形问题

代数式恒等变形属于解析式变换的一种,就是将一个代数式转变成另外一个同它恒等的代数式.在初中数学解题训练中,会经常安排几道有关代数式恒等变形类的试题,教师可提示学生应用待定系数法,按照实际要求对题目中的代数式进行恒等变形处理,让他们先把一个符合条件且含有待定系数的恒等式给假设出来,再借助恒等式的性质求出各个待定系数的具体值,也可以将待定系数消除掉,由此完成解题,这样解题过程显得十分清楚和简洁.

例7 已知有一个多项式xy(3x+2)(5y+2),请证明这个多项式是含有整数系数的两个多项式的平方差.

分析从本质看,本题需要把题设中的多项式通过两个整式的平方差形式表示出来,但是这两个整式属于未知条件,所以可设为A和B,随后借助待定系数法进行证明.

详解设xy(3x+2)(5y+2)=A2-B2,A、B均代表整式,则(3xy+2y)(5xy+2x)=(A+B)(A-B),令A+B=3xy+2y,A-B=5xy+2x,解之得A=4xy+x+y,B=-xy-x+y,所以说xy(3x+2)(5y+2)=(4xy+x+y)2-(-xy-x+y)2.

例8 已知多项式x4-6x3+13x2-12x+4,请证明该多项式能够通过完全平方式来表示.

分析这道题目中出现的是四次多项式,其应该是二次三项式的平方,所以可以假设原代数式恒等于(x2+px+q)2,该式子中的p与q便是待定系数.

详解设多项式x4-6x3+13x2-12x+4=(x2+px+q)2,化简变形后为x4+2px3+(p2+2q)x2+2pqx+q2,通过对应项系数的比较可以得到2p=-6,p2+2q=13,2pq=-12,q2=4,解之得p=-3,q=2,所以多项式x4-6x3+13x2-12x+4可以转变为(x2-3x+2)2.