基于机器学习的EPB盾构土仓压力预测方法研究

王 伟,王 兴,徐 亮,王 美 艳

(1.长春工程学院 土木工程学院,吉林 长春 130012; 2.吉林大学 建设工程学院,吉林 长春 130026)

0 引 言

土压平衡盾构(EPB)因其适用面广、对周边环境影响小的特点,在隧道施工中得以广泛应用。由于盾构法是封闭作业,其工作状态往往需要通过掘进参数来反映。选择合适的掘进参数可有效控制地面沉降和掌子面稳定,减少刀具的损耗,使盾构维持良好的姿态。同时,随着掘进过程中地质条件的改变,盾构掘进参数也需要进行实时调整优化,以确保盾构安全、高效地掘进。如何准确预测和控制掘进参数一直是盾构隧道施工技术领域的研究重点[1]。目前,许多学者针对EPB盾构掘进过程中刀盘扭矩、盾构推力、注浆压力、掘进速度等参数在不同地质条件下的变化规律及其理论计算开展了研究,并根据胡克定律建立了预测掘进参数的数学物理模型[2-7]。这些模型虽然能够反映掘进参数之间的解析关系,但是由于盾构掘进是一个复杂且不断变化的过程,其穿越的地层实际上是非均匀、不连续的非线弹性体,因此,这类预测模型在工程适用性上具有一定的局限性。随着近些年大数据与人工智能技术的快速发展,大数据统计分析[8-9]、BP神经网络[10-12]、遗传算法(Genetic Algorithm,GA)[13]、支持向量机(Support Vector Machine,SVM)[14-15]、随机森林(Random Forest,RF)[16-17]、粒子群(Particle Swarm Optimization,PSO)[18-19]等机器学习算法在盾构掘进参数预测研究中得以应用。上述研究表明,通过这些智能算法建立的预测模型其准确度明显高于数学物理模型,对于在不同地质条件下进行EPB盾构掘进具有重要的应用价值。土仓压力是EPB盾构施工中最重要的控制参数之一,土仓压力失衡将会造成掌子面失稳、地层缺失,进而引起地表沉降等一系列不良后果。在掘进过程中,盾构机的排土效率是刀盘扭矩、螺旋输送机转速、盾构推力、注浆压力等掘进参数耦合作用的结果,它直接反映了土仓压力的变化情况,而排土效率又受地层物理力学参数的影响随时变化,由于EPB盾构的土仓压力与其他掘进参数之间往往是非线性的映射关系,很难通过多项式拟合来确定土仓压力与其他掘进参数之间的函数关系。

鉴于此,本文将GA算法嵌入到PSO算法进行参数优化,综合考虑了盾构掘进参数之间的相互影响大、耦合效应强等特点[20],结合灰色理论建立基于灰色最小二乘支持向量机(Grey Least Square Support Vector Machine,GLSSVM)的土仓压力预测模型,并通过成都市地铁17号线砂卵石盾构隧道区间工程,以实际监测数据作为预测模型的训练与测试样本,验证预测模型的有效性和可靠性,为砂卵石地层EPB盾构施工掘进参数控制提供参考。

1 EPB盾构土仓压力预测模型

1.1 GLSSVM基本原理

LSSVM是在基于统计学习理论的机器学习算法基础上,通过求解线性方程组的形式来取代支持向量机中的二次规划优化。LSSVM模型是一种自适应模型,可将经验风险由一次方改为二次方,用等式约束代替不等式约束[21]。相比于传统的支持向量机,其优点在于提高了求解速度,使复杂计算简单化。GLSSVM模型是在LSSVM基础上结合灰色理论GM(1,1)对原始数据进行累加,进而得到受扰动因素影响更小、规律性更强的新序列数据。

假设原始监测数据序列如式(1)所示,采用GM(1,1)模型对数据序列进行累加预处理,得到累加序列值,如式(2)所示,由累加序列值建立LSSVM模型进行预测。设前n期的学习样本集合为A(xi,yi),i=1,2,3,…,n。其中,xi∈Rn表示学习样本,yi∈R表示相应的输出预测样本,则有高维特征空间描述如式(3)所示,其线性函数如式(4)所示。

(1)

(2)

(3)

y(x)=wTφ(x)+b

(4)

式中:w为权值向量;J(w,b,e)为损失函数;γ为容错惩罚系数;ei为误差;φ(x)为映射函数;b为偏置量。应用拉格朗日算子对w和e进行优化求解,建立拉格朗日函数如式(5)所示。

(5)

式中:αi为拉格朗日乘子,根据KKT(Karush Kuhn Tucker)最优条件对式(3)进行微分求解,得到线性方程组如式(6)所示。

(6)

式中:y=[y1,y2,…,yi]T;E=[1,1,…,1]T;α=[α1,α2,…,αi]T;Q为用于非线性映射的核函数,即Qij=K(xi,xj),i,j=(1,2,…,n);I为单位矩阵。求解方程组后得到LSSVM的回归模型,如式(7)所示。

(7)

通过计算,得到累加序列的预测值yn+k(k=1,2,…,n),对其进行累减还原,得到原始数据序列的预测模型,如式(8)所示。

(8)

1.2 PSO-GA参数寻优

核函数的选择对GLSSVM回归模型预测结果的准确性及其精度具有重要影响。GLSSVM回归模型通常采用高斯径向基核函数K(xi,xj)对非线性样本数据进行分析,如式(9)所示。

(9)

要在无先验参考值的前提下对未知数据进行正确的预测,必须对核函数的容错惩罚系数γ与内核参数σ2进行调整。目前,常使用GA、PSO算法进行参数寻优,但是两种算法都无法保证一定得到最优解。若将GA算法中的算子嵌入到PSO算法中,使具有优良变化能力的GA算法加入PSO算法的记忆能力,即可使整个种群向着全局最优的方向快速收敛[22]。

假设D维空间里的一群粒子,每个粒子都对应着一个能表征其属性的位置X和速度V,当第d次粒子群迭代更新后,粒子i的运动速度Vi和运动位置Xi的迭代更新如式(10)和式(11)所示。

(10)

(11)

式中:ω为惯性权重;i=1,2,…,m,d=1,2,…,D,其中,m为粒子的数量,D为搜索维度;c1和c2为加速度因子,其数值大小决定了寻优的时长,通常取正值;pBest,i为粒子i的最优位置;gBest,i为粒子群的最优位置;r1和r2为[0,1]之间的随机常数。

惯性权重ω的大小直接影响全局寻优和局部寻优的结果,为更好地平衡全局搜索能力和局部搜索能力,惯性权重可按式(12)计算。

(12)

式中:ωmax为最大惯性权重值;ωmin为最小惯性权重值;tmax为最大迭代次数;t为当前迭代次数。可见,将PSO和GA相结合进行参数寻优,兼具了GA算法的全局收敛和PSO算法的快速收敛的优点。

1.3 预测模型的构建与性能评价

构建GA-PSO-GLSSVM土仓压力预测模型的关键在于选择哪些掘进参数作为预测土仓压力的输入变量。由EPB盾构土仓压力的影响因素可知,总推力、刀盘扭矩、刀盘转速、推进速度、螺旋机转速、注浆量以及注浆压力皆与土仓压力有较高的相关性[23-25]。但是,不同的地质条件下,土仓压力与掘进参数之间的关系也有较大差异,需根据实际工程条件通过相关性分析来确定作为输入变量的掘进参数,并构建土仓压力预测模型。本文采用皮尔森相关系数(Pearson Correlation Coefficient,PCC)对土仓压力与各掘进参数之间的相关性进行定量描述。计算公式如式(13)所示。

(13)

式中:v为皮尔森相关系数;Y,Z为拟分析参数;p为数据组的数量。

为了验证预测模型的有效性,可采用平均绝对误差(MAE)、均方根误差(RMSE)、可决系数(R2)和平均绝对百分比误差(MAPE)来衡量预测数据与实际监测数据之间的偏差情况,如式(14)～(17)所示。若两个误差指标值越趋近0,表明预测模型的预测结果更准确,预测效果越好。土仓压力预测模型的拓扑结构如图1所示,预测流程如图2所示。

图2 GA-PSO-GLSSVM预测模型的预测流程Fig.2 Prediction process of GA-PSO-GLSSVM prediction model

(14)

(15)

(16)

(17)

2 案例验证

2.1 工程概况

成都市地铁“市五医院站”至“凤溪河站”区间隧道起点位于凤溪大道北段和西凤街交叉口,沿凤溪大道程南北向布置,采用土压平衡盾构机进行双线掘进。其中,左线隧道长1 610.186 m,右线隧道长1 611.485 m,左右线各使用1台EPB盾构机。本区间隧道主要穿越密实卵石土层,隧道纵坡坡度为10.063‰,最小平面曲线半径450 m。隧道内径7 500 mm,隧道外径8 300 mm,区间隧道顶最小埋深约9.5 m,最大埋深约20 m。盾构机主要性能参数下:

盾构机外径 8 580 mm

推进油缸 2 000 kN,2 200 s,35 MPa,(2×19)

全油缸运行速度 80 mm/min

刀盘扭矩 24 324.3 kN·m(α=37.8)

刀盘转速 2.8 r/min

螺旋机转速 20 r/min

排土量 684 m3/h

砂卵石地层是一种力学性质极其复杂的地层,具有颗粒间空隙大、黏聚力低的特点,盾构机的掘进使地层产生非常大的扰动,必须对掘进参数进行精确控制。盾构掘进过程中,每开挖1环可获得1组监测数据,数据组由总推力、刀盘扭矩、推进速度、螺旋机转速、螺旋机扭矩、注浆量和土仓压力组成。根据实际监测数据可知,该区间共有1 033组数据,取101～1 000环共计900组数据进行统计分析,统计分布如表1所列。

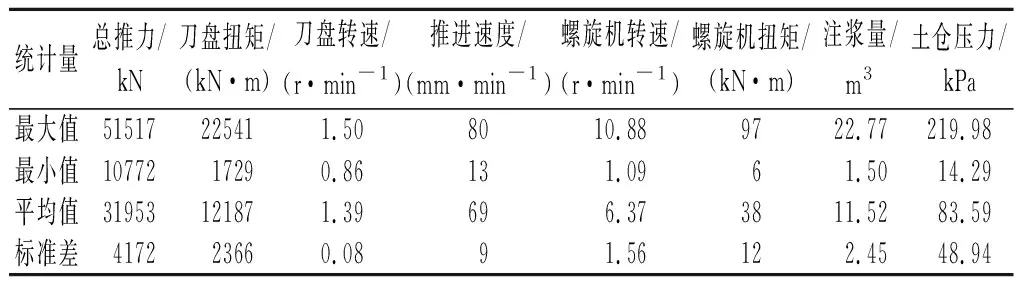
表1 盾构区间掘进参数统计分布Tab.1 Statistical distribution of tunneling parameters in shield section

去除数据集中前期盾构试掘进和后期出洞调整数据,选取220～855环共计635组数据进行研究,绘制各掘进参数的正态分布图,如图3所示。

图3 掘进参数正态分布Fig.3 Normal distribution of tunneling parameters

图4 样本数据集土仓压力分布Fig.4 Distribution of chamber earth pressure in sample data

2.2 掘进参数相关性分析

运用Pearson相关系数描述土仓压力与各掘进参数的相关性,按照式(13)计算相关系数,计算结果如表2所列。

表2 土仓压力与各掘进参数的Pearson相关系数值Tab.2 Pearson correlation coefficient between chamber earth pressure and excavation parameters

由计算结果可知,土仓压力与总推力、刀盘扭矩和螺旋机转速呈负相关关系,与刀盘转速、推进速度、螺旋机扭矩和注浆量呈正相关关系。对计算得到的相关系数进行检验,根据当|r|≥rɑ时两因素在置信水平ɑ下相关可知,刀盘扭矩、刀盘转速、螺旋机转速与土仓压力在0.01水平上显著相关,而总推力、推进速度和注浆量在0.1水平上显著相关,而螺旋机扭矩与土仓压力相关性不显著。因此,土仓压力预测模型的输入变量为刀盘扭矩、刀盘转速、螺旋机转速、注浆量、推进速度和总推力。

2.3 预测模型的建立

将635组数据中的前535个数据作为训练集,最后100个数据作为测试集,并对学习样本集数据进行GM(1,1)模型累加预处理,建立GLSSVM模型。利用MATLAB软件将GA算法的交叉算子和遗传算子嵌入PSO算法中,并对GLSSVM模型核函数的容错惩罚系数γ与内核参数σ2进行优化处理。参数设置时,种群数量过少会产生病态基因,过多又会增加计算量,一般设置为0～200。相应的,进化代数过小会导致算法不易收敛,代数过大则算法不能收敛,所以常取100～500。 变异概率设置时,如果数值过小,容易导致有效基因的迅速丢失且不容易修补,而变异概率过大,虽然保证了种群的多样性,但高阶模式被破坏的概率也随之增大。因此,基因突变的概率在0.001～0.1之间取值。与变异概率相似,交叉概率过大随机性增大,容易错失最优个体,而交叉概率过小则无法有效更新种群。因此,交叉概率的取值为0.3～0.9。经过调试,最终确定迭代次数为300,种群规模为30,交叉概率为0.6,变异概率为0.1,两个优化参数的取值范围设为[0.01,1 000]。

惯性权重可以影响微粒的局部最优能力和全局最优能力。惯性权重大有利于提高全局搜索能力,反之会增强局部搜索能力。惯性权重按照式(12)进行迭代寻优,其最大值为0.9,最小值为0.4。局部搜索能力c1和全局搜索能力c2决定了微粒的经验信息对其运行轨迹的影响,反映了微粒群之间的信息交流。如何确定最优参数是个复杂的优化问题,通常需要反复试算来确定。为了使粒子的个体经验和群体经验有同样重要的影响力,使算法达到全局探测与局部开采两者间的有效平衡,可令c1和c2取值相等[26]。本案例通过调试c值,对比不同方法的最佳适应度,并根据最快收敛速度和最佳适应度原则,最终确定c1=c2=1.494 45,即工作最为出色的参数组合。

分别对GA-GLSSVM,PSO-GLSSVM,GA-PSO-LSSVM,GA-PSO-GLSSVM四种模型进行预测分析,其适应度MSE的变化规律如图5所示。

图5 不同算法的适应度变化Fig.5 The fitness changes of different algorithms

从各模型适应度曲线可知,GA-GLSSVM模型的全局搜索能力更强,PSO-GLSSVM模型的收敛速度更快。PSO算法进行函数寻优时,常常出现早熟现象,导致求解函数极值存在较大的偏差,然而遗传算法对于函数寻优采用选择、交叉和变异算子操作,直接以目标函数作为搜索信息,以一种概率的方式来进行,因此将GA算子嵌入PSO算法中,可实现GA算法的全局优化优点,又能发挥PSO加快收敛速度的优势,提高模型拟合优度。同时本文提出利用灰色理论对原始数据进行预处理,可获得受扰动因素影响更小、规律性更强的新序列数据。不同模型最优参数组合容错惩罚系数与内核参数如表3所列。

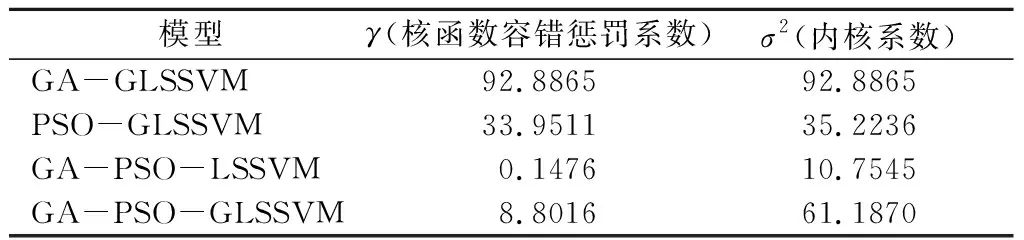
表3 不同模型的最优参数组合Tab.3 Optimal parameter combinations of different models

2.4 预测结果分析及对比

将各个模型的优化参数带入LSSVM模型进行预测分析,利用GM(1,1)模型进行预处理的数据将得到累加序列预测值,对预测值进行还原,即为原始数据集的预测数据。在相同拓扑结构、训练集等条件下利用BP神经网络进行预测并进行对比分析,预测结果如图6所示。

图6 不同模型的预测效果对比Fig.6 Comparison of prediction effects of different models

通过对比可知:BP神经网络模型在进行土仓压力预测时,预测结果波动较大,适用性较差;PSO-GLSSVM模型的预测数据较为平稳,波动较小,但预测结果较实际值偏小;GA -GLSSVM预测结果后期波动相对较大,且预测结果较实际值偏大;GA-PSO-GLSSVM模型兼顾了上述两种模型的优点,预测结果与实际值十分接近;而GA-PSO- LSSVM模型的预测结果波动性大,且精度较低。为验证灰色理论预处理的有效性,剔除学习样本集中个别较大数据,剩余524个数据分布如图7所示。

图7 剔除波动较大的数据土仓压力分布Fig.7 Distribution of chamber earth pressure by excluding the data with large fluctuations

令模型参数不变,将前424个数据作为训练集,后100个数据作为测试样本进行GA-PSO-LSSVM预测,结果如图8所示。由图8可知,在预测初期数据波动较小时,GA-PSO-LSSVM模型的预测效果较好,但由于模型的抵抗波动能力较弱,以及前期误差的累计,导致后期预测效果不佳。但与图6中GA-PSO-LSSVM的预测结果相比,在剔除个别较大值后,模型的预测数据波动降低,预测精度提高,可知原始数据的波动会极大影响模型的预测效果。本文将灰色模型引入最小二乘向量机,对原始数据进行累加处理,消除原始数据波动的影响,提高了预测精度。

图8 剔除波动较大的数据GA-PSO-LSSVM模型预测效果Fig.8 The prediction effect of the GA-PSO-LSSVM model after eliminating data with large fluctuations

砂卵石地层因其透水性强,自稳性差,受到扰动时极易引起地层损失,因此,掘进过程中影响土仓压力的因素非常多,尤其是遇到大粒径卵石或排渣不畅时,极易造成土仓压力的异常波动。通过对比分析可知,BP神经网络对土仓压力的预测效果较差,GA-GLSSVM、PSO-GLSSVM和GA-PSO- LSSVM 3种预测模型在初始阶段的预测精度和预测效果还是比较好的。当遇到波动数据时,其土仓压力预测值与实测值偏差较大,可见,掘进情况的突变影响了预测模型的学习效果,导致预测精度明显下降。而GA-PSO-GLSSVM模型较好地削弱了数据波动对于预测模型的影响,在砂卵石这类复杂地层中预测EPB盾构土仓压力参数具有显著的适用性。

2.5 误差分析

为了进一步检验模型的可靠性与精确性,以均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、可决系数(R2)为评定指标对预测模型进行精度评定。由表4可知,BP神经网络预测模型和未处理数据的GA-PSO- LSSVM模型的预测结果R2为负值,对土仓压力预测的适应性较差。通过各模型预测精度对比可知,GA-PSO-GLSSVM土仓压力预测模型的稳定性、拟合精度以及结果的准确性均高于其他模型,可见该算法可以有效预测EPB盾构的土仓压力,采用GM(1,1)预处理后的预测效果要优于传统预测模型。

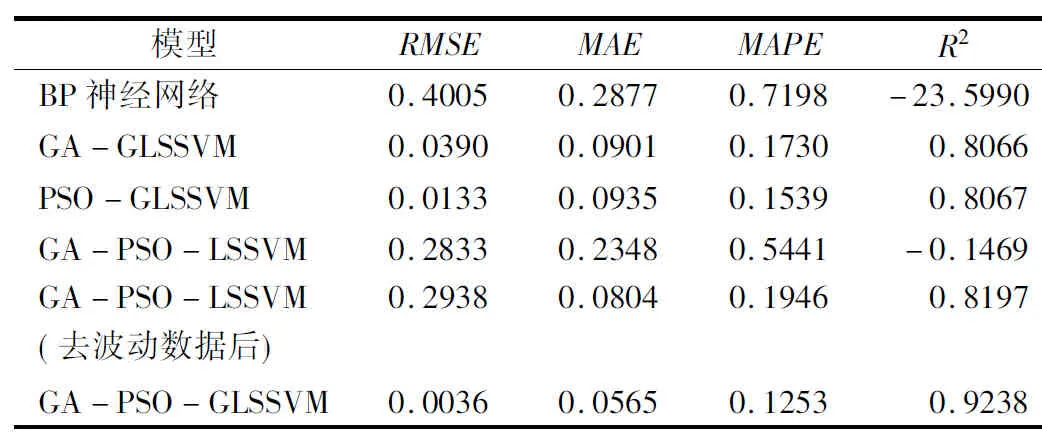
表4 各模型预测精度对比Tab.4 Comparison of prediction accuracy of each model

3 结 论

(1) 本文将GA算子嵌入到PSO模型中,对数据的参数寻优过程进行了优化。该方法结合了GA算法全局搜索能力和PSO算法快速收敛的优势,避免了参数寻优陷入局部最优解,加快了运算效率。同时将GM(1,1)模型引入LSSVM模型,消除了数据波动对预测模型的影响,提高了GA-PSO- GLSSVM土仓压力预测模型的精度。

(2) 对比GA-GLSSVM、PSO-GLSSVM、GA- PSO-LSSVM和GA-PSO-GLSSVM四种模型的预测结果可知,GA-PSO-GLSSVM模型预测结果更加平稳,相较于其他3种模型,均方根误差、平均相对误差、平均绝对百分比误差和可决系数均明显优于其他模型,预测精度更高。

(3) 通过筛选出总推力、刀盘扭矩、推进速度、螺旋机转速、螺旋机扭矩和注浆量6种掘进参数,利用GA-PSO-GLSSVM模型对盾构掘进土仓压力进行了预测。以实际监测数据作为预测模型的训练与测试样本,验证了预测模型的有效性和可靠性。合理而准确的土仓压力预测可以有效避免因土仓压力失衡造成的掌子面失稳、地层缺失,进而引起地表沉降等一系列不良后果。