基于最优决策树的多能系统快速鲁棒优化调度
彭浩晋,邱 高,税 月
(1.四川大学电气工程学院, 四川 成都 610065;2.国网四川省电力公司技能培训中心, 四川 成都 611133)
0 引 言
对于包括风能、太阳能、水力资源和其他可再生能源的具有多维不确定性的互补发电系统的协调调度[1-3],通常采用随机优化[4]和鲁棒优化[5]方法进行建模和处理。
随机优化可以用于具有多不确定性的可再生能源发电调度过程的定量分析,但由于对混合可再生电力系统中不确定性概率分布规律进行精确描述十分困难[6],随机优化需要预先设置概率分布类型[7],这在一定程度上降低了其可靠性。除此之外,随机优化基于大量离散场景,将使计算规模过大,从而导致更长的消耗时间和较低的计算效率[8]。尽管离散场景的场景约简技术[9]和Benders分解加速方法[10]可以减少计算规模,但这些方法不能覆盖所有实际场景,并且所获得场景的代表性和典型性值得怀疑,那么解的准确性也会降低。
相较而言,鲁棒优化不需要预先设置随机变量的概率分布[11-13],它通过不确定变量的边界参数来描述随机变化特征[14],只要变量值在边界内,就可以从鲁棒优化模型中获得可行的解。与随机优化相比,鲁棒优化可以为边界内任意取值的不确定变量获得可行解[15],并能严格保证决策的可靠性,同时计算规模大大缩小,数据需求也减少。但由于鲁棒优化是基于最坏的情况来搜索最优值[16-17],因此鲁棒优化存在优化结果过分保守的缺点,这将导致在水风光多能互补调度中不能充分利用资源。
针对随机优化、鲁棒优化在处理水电、风能和太阳能等可再生能源的不确定性特征过程中存在的问题,相关研究人员尝试将随机优化和鲁棒优化结合起来,使其优势互补并避免两种方法的缺点。此外,随着测量技术的不断改进,电力系统产生了大量的多类型生产数据。在此背景下,数据驱动的分布式鲁棒优化(distributionally robust optimization,DRO)应运而生,这为解决随机优化模型的低精度和鲁棒优化模型的保守性提供了新的途径[18]。目前,DRO技术已初步应用于电力系统的机组组合[19]、多能互补调度[20]等,也有相关研究简化了DRO的复杂计算过程[14]。与随机优化和鲁棒优化相比,DRO不需要获得变量的精确概率分布,只需要构建一个覆盖真实分布的不确定集,并在最坏分布下进行决策,从而避免了变量的复杂概率分布难以获得的难题。此外,通过采用线性决策规则、拉格朗日对偶处理[21]等技术,可以将DRO问题转化为确定性优化问题,以避免随机优化方法的大采样规模和低计算效率问题。DRO的显著优点是它覆盖了不确定参数的概率统计信息,并可以提高决策的保守性。DRO不仅结合了随机优化的概率统计特性,还借鉴了鲁棒优化的思想,其决策结果具有抗风险性能,在处理电力系统的不确定性特征方面具有独特的显著优势[16]。
鉴于数据驱动DRO在不确定经济调度、低碳调度和机组组合领域的独特优势,下面提出了一种基于最优决策树的DRO的梯级水电与风/光新能源电站联合系统协调优化调度方法(two-stage distributed robustness based on optimal decision tree,ODT-DRO)。该方法首先建立了数据驱动的两阶段DRO调度模型,第一阶段考虑系统的互补经济调度成本,第二阶段考虑系统实时调整能力,并引入范数约束来限制风电与太阳能的不确定输出的概率分布置信集,以寻求最差分布情况的最优解。同时,通过嵌入基于优化理论的可解释的最优决策树算法[22-24]实现机组状态和出力水平的日内快速决策,实现模型热启动有效提升日内决策效率。
1 基于数据驱动的两阶段DRO水风光互补协调调度模型
1.1 模型目标函数
基于数据驱动的两阶段分布鲁棒优化水风光互补协调调度模型包含两个阶段,第一阶段为机组组合模型,第二阶段为实时调整模型。模型目标函数如式(1)所示。
(1)
式中:pk为第k个离散场景的概率;K为离散场量总数;Cuc与Cre分别为机组运行成本和实时调整成本。
可以看出,式(1)是一个min-max-min三层的两阶段鲁棒优化问题,与仅针对最坏情况进行优化的传统两阶段鲁棒优化相比,该模型的内部max、min函数通过优化决策变量来计算K个离散情况的最坏概率分布,并获得最大期望成本值。Cuc与Cre分别由式(2)和式(3)计算得到。
(2)
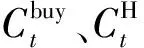
(3)
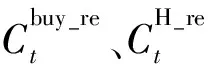
1.2 考虑经济调度和综合范数的约束条件
模型的约束主要分为3种类型:常规运行约束、实时经济调整约束和数据驱动的综合范数约束。基于梯级水电系统和风/光系统的预测信息形成的运行约束主要包括功率平衡约束、水量平衡约束、机组运行约束、电网约束[25]和备用约束等。由于实时阶段的不确定性,需要调整梯级水电的输出,以平衡风光出力的随机波动。因此引入实时调整约束,如式(4)—式(12)所示,分别表示实时调整阶段的源-荷平衡约束、水库蓄水量变化约束、梯级水电有功输出约束、排放流量约束、水量平衡约束、级间液压连接约束、水轮机爬坡率约束、风力/光伏电站的有功约束以及网络约束。
(4)
(5)
(6)
(7)
Vi,t+1+ΔVi,t+1,k=
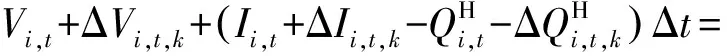
(8)
(9)
(10)
(11)

(12)

由于传统的求解方法对于求解上述DRO优化调度模型来说过于复杂,引入了一种基于1-范数和∞-范数的数据驱动的DRO算法来求解模型。首先,该算法以水力径流和风力/光伏强度等不确定参数的历史数据为参考,通过提取有限典型日的水力和风力/光伏历史数据,筛选K个离散场景的水力和风/光发电量以及每个场景的初始概率;然后,以每个初始概率分布为中心,引入综合范数约束来计算该联合优化问题,从而获得每个离散场景的最坏概率分布,并获得该场景下的最大期望目标值。因此,在数据驱动的两阶段DRO协调调度模型中,除了常规运行调度约束和实时调度约束外,还需要考虑综合范数约束。
由1-范数和∞-范数对水风光随机输出的离散场景施加了约束,Ω为综合范数的可行域,可用式(13)表示。
(13)
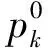
(14)
(15)
式中:α1和α∞分别为1-范数和∞-范数约束下离散场景集的概率分布置信系数;M为选定的有限典型水风光发电场景日数。根据式(13)和式(14),约束水风光不确定性输出的允许偏差限值θ1和θ∞是可以获得的,如式(16)所示。
(16)
2 最优决策树模型
鲁棒优化受初值影响较大。若可将初值设置在最优解附近,则鲁棒优化的搜索范围将极大减小,从而可有效提升多能系统的调度效率。下面通过引入可解释性较强的最优树方法,建立以风、光、荷等实时量测值为输入、机组出力和机组组合为输出的决策树映射,实现对鲁棒调度决策变量的实时“热启动”优化初始化。
决策树模型基于树结构对特征进行拆分,能够实现数据的分类与回归任务,具有可解释性强的优点[28-31]。这里使用混合整数规划(mixed integer programming,MIP)搭建最优决策树模型,相较于经典的决策树算法(classification and regression tree,CART),最优决策树模型在树的顶部做出的决策也会影响全局最优解,而不是简单地做出一系列局部最优决策,避免了对决策树采取修剪和杂质措施。并且模型为混合整数规划问题,可以通过MIP解算器,如Gurobi和CPLEX进行求解。
搭建MIP的最优决策树可概述为建立分支结点与叶结点的精细参数化决策规则以及约束条件,并明确最终优化函数目标,最后通过MIP解算器求解。搭建的最优决策树结构如图1所示。
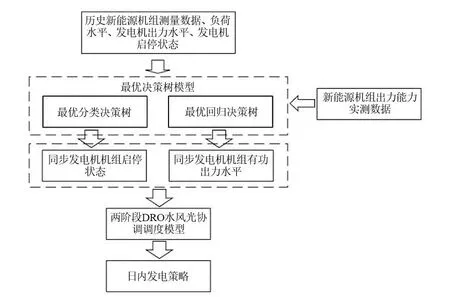
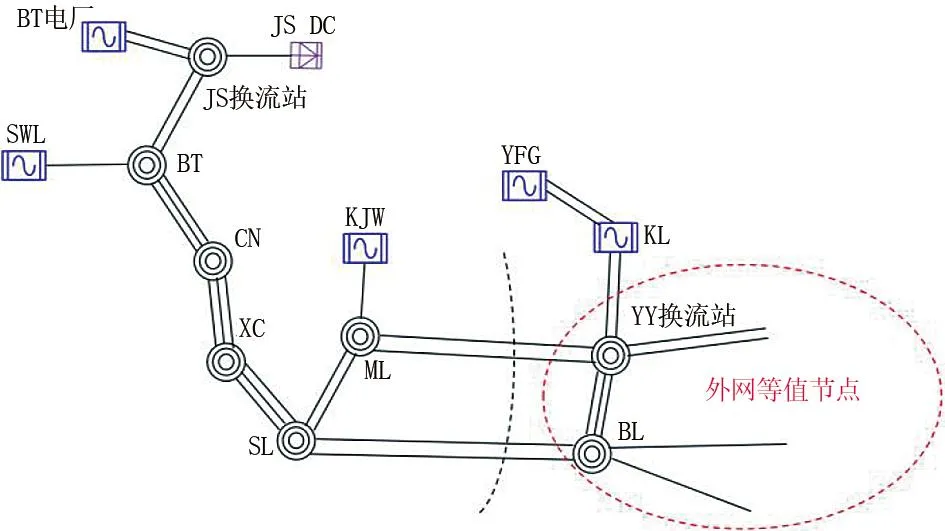
图中,a为分支选择状态变量,且a∈{0,1};b为分支判别变量。分支结点的拆分遵守aTx ds≤dp(s), ∀s∈TB (17) (18) 0≤bs≤ds, ∀s∈TB (19) ars∈{0,1},r=1,…,p, ∀t∈TB (20) 式中:ds为结点s的分支指示变量,其取值只有0和1,表示不可拆分或可拆分;p(s)为结点s父结点;TB为决策树的分支结点集合;p为样本包含的特征总数;r为特征序号;ars为二进制变量,用以确保每个结点只允许对一个变量(即样本属性)进行拆分;bs为在分支结点s上进行拆分的判断阈值条件,作为连续变量,因为样本特征属性是归一化的结果,所以bs取值也在0和1之间。式(17)表示当分支结点的父结点不可拆分,那么分支结点也必定不能拆分;式(18)表示在分支结点上一次只能针对一个属性进行拆分。 通过上述规则和引入的变量可以能够实现MIP的树结构建模,同时还需要建立叶结点的分配规则,将叶结点与样本类别相匹配。通过引入二进制变量zms=1来标志有样本m落入叶结点中,样本总数为n,并引入二进制变量ls=1表示叶结点满足最小落入样本数,最小样本数为Nmin,并且需要强制每个样本点只能分配给一个叶结点,因此有如下约束: zms≤ls,s∈TL (21) (22) (23) 式中:zms为叶结点样本指示变量,zms=1表示样本xm落在结点s,以此来跟踪分配给每个叶结点的样本;ls为叶结点最小样本数限制指示变量,与叶结点最小样本数Nmin构建最小样本数限制;TL为叶结点集合。 最后在将样本分配给叶结点时需要用强制约束进行拆分: (24) (25) 式中:M1与M2都为任意大的常数;AL(s)为叶结点的拆分路径上的左分支结点集;AR(s)为叶结点的拆分路径上的右分支集;v为左分支结点或右分支结点的索引;ò为引入的小常数,满足MIP解算器的不等式要求。 通过上述模型,需要最小化每个叶结点中误分类样本的个数Lt,线性化表达为: Ls≥Ns-Nus-M(1-cus), (26) Ls≤Ns-Nus+Mcus, (27) Ls≥0, ∀s∈TL (28) 式中:Ls为误分类损失,其值为叶结点样本总数减去比例最多标签样本数;Ns为叶结点上总的样本个数;Nus为叶结点上第u类样本的个数;通过找到叶结点中样本数最多的类,确定该类为叶结点所对应的类别,最小化错误分类样本个数,引入cus=1表示叶结点s对应类别为u;M为任意大常数,结合cus的取值使约束无效。 根据基线精度标准化错误分类,得到模型的优化目标为 (29) 式中,α为复杂性参数,控制树的精度与复杂性。 构建的最优决策树模型为混合整数规划问题,能够有效嵌入数据驱动的水风光两阶段分布鲁棒模型中。根据新能源实测数据进行运行方式快速决策,提供给模型进一步优化,解释性强,可通过Gurobi和CPLEX等求解器进行求解。 使用ODT-DRO实现水风光多能系统协调调度。首先,需要通过大量历史新能源出力水平、负荷水平、发电机出力水平、机组启停状态等数据作为最优决策树训练数据输入特征,分别得到最优分类决策树与最优回归决策树;最优分类决策树与最优回归决策树根据新能源机组出力能力实测数据分别输出同步发电机组启停状态与出力水平,将同步发电机启停状态与出力水平传递给两阶段DRO水风光协调调度模型,进一步优化得到日内发电策略,具体流程如图2所示。 图2 联合优化方法流程 由于最优决策树模型通过离线训练得到,对新能源实测数据能够快速给出发电机出力和状态的决策结果,实现对两阶段DRO水风光协调调度的加速,避免由于新能源预测误差对调度结果的不利影响,实现多能互补系统的日内发电策略快速决策。 将所提ODT-DRO模型在四川ZD地区电网的试验应用,验证所提方法多能互补协调调度可行性。ZD地区等值系统如图3所示,根据拓扑结构与基础数据将该系统简化为29个母线节点的系统,包含BT、SWL、KJW、YFG与KL等发电厂。参考攀西新能源大发运行方式作为基准运行方式,该运行方式下GN并网1700 MW,ZD地区汇集站光伏并网600 MW,金上直流外送功率为5000 MW。 图3 ZD地区等值系统 引入最优分类决策树,根据新能源实测数据、负荷水平以及水电机组实际运行条件对同步机组启停状态进行决策。最优决策树树结构最大深度为5,最优分类决策树进行分支的最小样本数为10,最优回归决策树采用均方差来进行评估。最优决策树算法在分类准确率达到99.52%且训练样本数据量充足的情况下,能精确地决策机组启停状态。相比于经典的CART算法,其准确率提升了5.18%,如表1所示。 表1 CART决策树与最优决策树分类准确率 通过最优回归决策树拟合不同运行环境下同步机组有功出力,并与CART决策树拟合结果进行对比,如图4所示。由图4可以看到:CART算法拟合后得到的发电机出力曲线与实际曲线存在较大误差;使用最优决策树进行拟合后得到的发电机出力曲线与实际曲线贴合度较高,误差较小,拟合效果更好。 图4 两种决策树算法拟合效果 通过最优分类决策树与最优回归决策树得到同步发电机组启停状态和出力结果。将该结果传递给两阶段DRO水风光协调调度模型作为初始解,实现热启动,加速模型优化求解速度。相较于没有嵌入最优决策树的模型,所建模型求解时间节省了231.752 3 s,如表2所示。 表2 模型求解时间对比 在不考虑新能源消纳受阻情况下,以ZD地区风机出力能力为例,对比日前调度与所提ODT-DRO模型对新能源机组优化出力与实测数据的偏差,如图5所示。从图5可以看到:日前调度通常根据未来一天新能源预测曲线对未来一天的发电计划进行优化计算,因此新能源预测误差较大,与实际测得的新能源出力水平曲线有较大偏差;所提ODT-DRO调度方法根据当前时刻新能源机组出力水平的实测数据进行决策,时间尺度短,预测误差与调度误差较小。 图5 两种模型调度误差与预测误差分析 ODT-DRO水风光协调调度结果如图6所示。可以看到所提模型能够在四川电网ZD地区完成水风光多能协调互补调度,并且在新能源机组出力水平较高的时间段(10:00—16:00),降低同步发电机组出力甚至关停部分机组,为新能源机组让出更多空间,防止出现新能源消纳受阻的情况,验证了所提模型在多能互补系统中调度的合理性和可行性。表3是部分调度结果展示。 表3 部分调度结果展示 单位:MW 图6 模型优化调度结果 表4比较了所提ODT-DRO算法、随机优化算法以及传统鲁棒优化算法的调度成本。ODT-DRO单位调度成本为148.721 6元/MWh,远低于传统鲁棒优化算法单位平均调度成本,也略低于随机优化算法的单位平均调度成本。因此,所提出的ODT-DRO协调调度方法更具经济性。 表4 模型调度成本对比 为了在包含多清洁能源的系统中实现水风光多能互补调度,并且在防止调度结果过度保守的同时实现以新能源优先消纳为目标的日内发电策略快速决策,提出了基于最优决策树的两阶段DRO水风光协调调度模型。该模型考虑实时调整能力以及范数约束,避免了调度结果的过分保守。同时,嵌入的最优决策树模型根据新能源实测数据、负荷数据以及实际运行情况,为两阶段DRO提供了同步发电机启停状态与出力决策,加速两阶段DRO求解,实现日内发电策略快速决策。通过在四川某地区电网的试验验证了所提模型的有效性,该模型在求解速度、决策精度、调度成本、安全稳定性以及鲁棒性上都有较好的表现,能够快速给出可靠的日内调度辅助决策信息。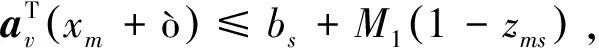
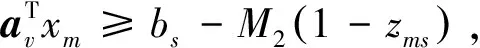
u=1,…,U, ∀s∈TL
u=1,…,U, ∀s∈TL3 ODT-DRO联合优化调度方法
4 算例分析
4.1 最优决策树算法分类与回归效果分析


4.2 模型求解时间

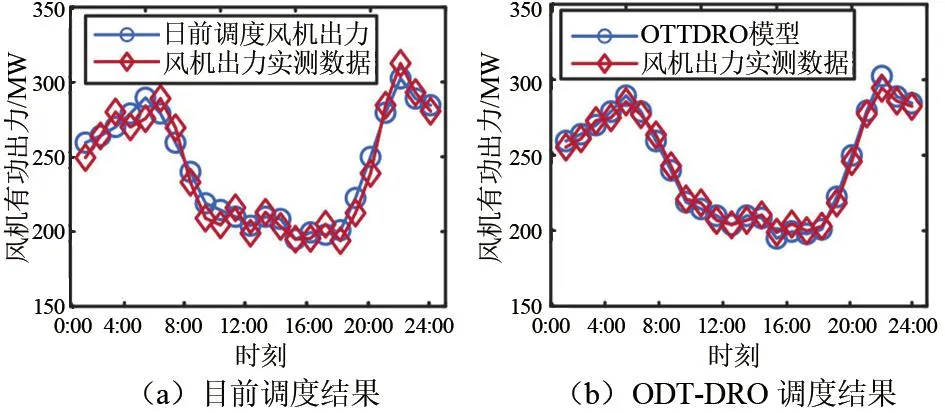
4.3 新能源机组调度出力偏差分析
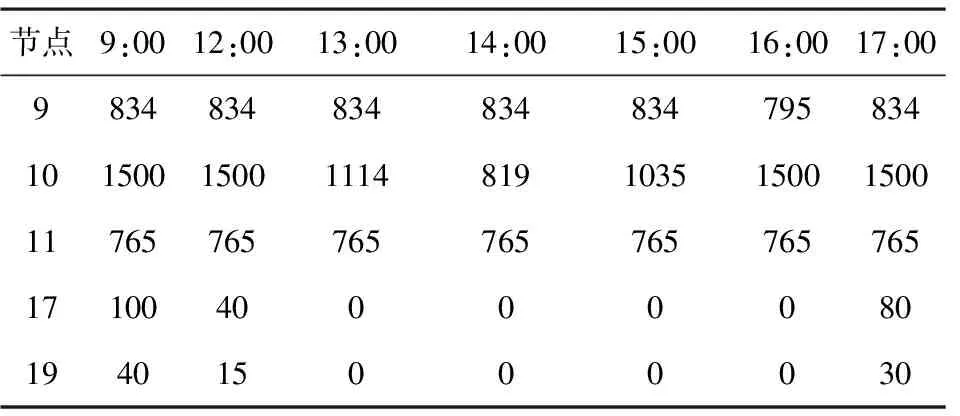
4.4 ODT-DRO优化调度结果分析

4.5 模型成本分析

5 结 论

