非稳态二维扩散方程的高次有限元黄金比例有限差分格式求解
孙美玲, 丁 晓, 江 山*
(1. 南通大学理学院, 江苏 南通 226019; 2. 南通职业大学基础部, 江苏 南通 226007)
非稳态对流扩散反应问题广泛存在于流体力学、空气动力学、化工制造、生态环境及运筹控制等领域, 其模型方程含有时间导数项、空间二阶/一阶导数项和右端非稳态项, 其中的非对称项增加了理论分析与数值求解的难度.由于非稳态对流扩散反应方程的解析解通常难以得到, 所以有效且实用的数值求解方法便显得尤为重要.近年来, 非稳态扩散问题常用的数值求解方案主要有有限差分法[1-3]、有限元法[4-5]、间断有限元法[6-7]、有限体积法[8-9]、时空有限元法[10]和虚拟元方法[11]等.例如, Gupta等[1]仅构造了单一的有限差分格式求解含参数的抛物型对流扩散问题; Lin等[4]提出对流扩散反应方程的一种稳定化有限元逼近方法, 但计算量偏大.本文拟构造高次有限元并结合有限差分的数值隐格式求解非稳态对流扩散问题.在选择有限差分参数θ时不再简单使用Euler向后差分或Crank-Nicolson六点对称等格式, 而是选择具备美学特性的黄金分割比例差分格式进行时空间的全离散, 以期实现数值计算的高阶精度与稳定收敛.
1 模型方程及其变分形式
考虑二维非稳态对流扩散反应方程[4-5]
(1)


(2)
其中n为外法线向量, ds表示曲线积分.
令检验函数v(x,y)在∂Ω上为零.于是, 问题(1)转化为: 寻找试探函数u(x,y,t),须满足
(3)
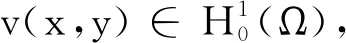
(ut,v)+a(u,v)=(f,v)
(4)
2 空间尺度的有限元格式
在有限元格式下完成变分形式(4)的与空间尺度有关的半离散化格式[4-5].在空间区域Ω的x、y方向进行一致剖分, 并在剖分后的单元上构造合适的有限元基函数φj(j=1,2,…,Nb), 其中Nb为全局基函数的总数目.以基函数φj为基底张成有限维逼近空间Uh, 且Uh⊂H1(Ω).分别选用二维Lagrange型线性元和二次元作为有限维空间的基函数进行比较.为了阐述清晰, 以更复杂的二维二次元基函数为例, 进行空间尺度下的有限元空间构造.
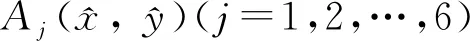
(5)
在δ-准则限定下, 可求得参考单元的6个局部基函数为
(6)
实际单元的顶点记为(xi,yj)(i=1,2,3;j=1,2,3), 通过仿射变换建立参考单元与实际单元之间的对应关系:
(7)

(8)
其中对应的仿射变换为
(9)
以式(8)所示的局部基函数ψni(x,y)为基底张成局部有限元空间Sh(En)=span{ψn1,ψn2,ψn3,ψn4,ψn5,ψn6}.在剖分形成的每一个全局节点xj(j=1,2,…,Nb)对应定义全局基函数φj, 使得i,j=1,2,…,Nb时有φj|En∈Sh(En)且满足
(10)
令Tb为所有单元的全局节点对应的数据索引, 则
(11)
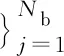
(uht,vh)+a(uh,vh)=(f,vh),
(12)
进一步可得
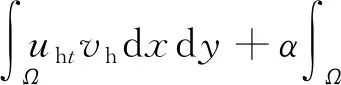
(13)
(14)
求解得到待定系数uj(t).令
(15)
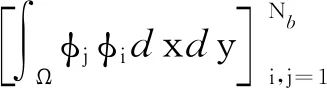
MX′(t)+A(t)X(t)=b(t).
(16)
由于基函数φj与检验函数φi只与空间变量x,y有关,A(t)及b(t)随时间t的变化关系取决于系数α、β、γ和源项f, 且在某个确定时刻A(t)和b(t)退化为仅依赖于空间.
3 时间尺度的黄金比例有限差分格式
采用有限差分格式[12]处理时间尺度.有限差分格式的类型由参数θ的取值确定, 如θ=0时, 为Euler向前差分显格式;θ=1时, 为Euler向后差分隐格式;θ=0.5时, 为Crank-Nicolson六点对称隐格式.本文将突破固有的差分格式, 通过构造与θ取值有关的全离散格式, 研究不同取值时差分格式下的优化数值精度结果.
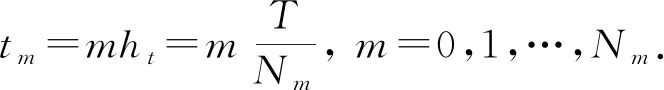
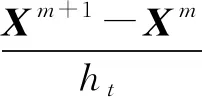
(17)
当式(15)中的系数α,β,γ与时间无关时,A(t)不依赖于时间, 简记为A.定义Xm+θ=θXm+1+(1-θ)Xm, 有
(18)
将式(18)代入全离散格式(17), 化简可得
(19)
定义
(20)
(21)
将式(20)(21)代入式(19), 即得全新的与时间有关的全离散线性代数系统:
BXm+θ=d,m=0,1,…,Nm-1.
(22)
求解式(22)可得未知向量组Xm+θ.
本文将数学与美学相结合, 对参数θ取黄金分割比例值0.618, 数值验证黄金比例下全离散格式的数值精度优势.
4 数值算例
运用MATLAB 2020b软件编写数值算例程序, 硬件环境为Intel Core i9-10900K CPU 3.70 GHz, 32 GB RAM.
设置非稳态问题(1)中系数α=γ=1,β=(1,1)T, 则其精确解为
u(x,y,t)=-cos(πy)ex+t,
(23)
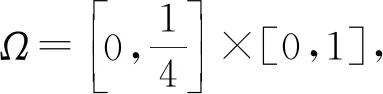
(24)
对于具有精确解的二维非稳态对流扩散反应问题(24), 在空间尺度上使用有限元格式的线性基函数与二次基函数分别进行半离散化, 在时间尺度上取θ=0.618的黄金比例有限差分格式进行全离散化.为了衡量新的混合格式下数值解uh对真解u的逼近效果, 计算两者误差的L∞范数、L2范数与H1半范数:
‖u-uh‖∞=supx,y∈Ω|u(x,y,t)-uh(x,y,t)|,
(25)
(26)
(27)
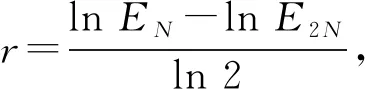
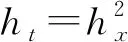

表1 θ=0.618时, 线性有限元误差的L∞范数、L2范数、H1半范数和收敛阶

表2 θ=0.618时, 二次有限元误差的L∞范数、L2范数、H1半范数和收敛阶
为更直观地对比, 图1给出了θ=0.618, 空间剖分数N=24,t=0.25 s时方程(1)的真解与线性有限元解、二次有限元解之间的离散节点绝对误差.由图1可知: 在t=0.25 s,N=24时, 线性有限元的最大误差数量级为10-4, 而二次有限元的最大误差数量级为10-6且误差远低于线性有限元的,表明相同条件下二次有限元格式的精度优于线性有限元.
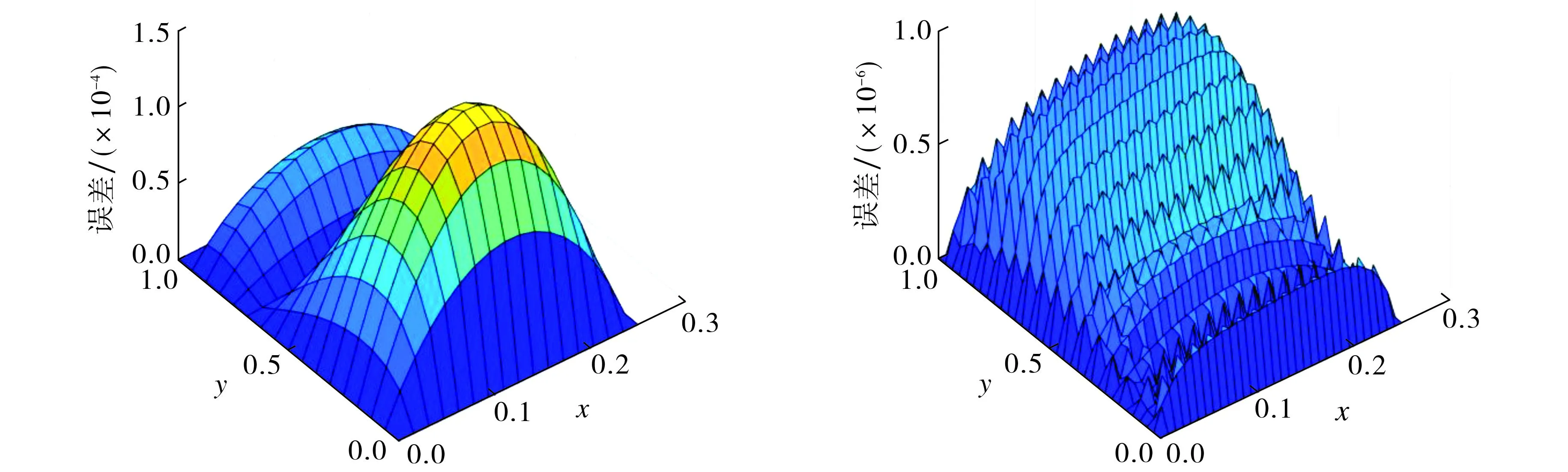
图1 θ=0.618, t=0.25 s时, 线性有限元(a)与二次有限元(b)在N=24下的绝对误差Fig.1 When θ=0.618, t=0.25 s, absolute error of linear finite elements (a) and quadratic finite elements (b) on partition number N=24
5 结语
本文提出空间高次有限元法结合时间全离散的黄金比例有限差分隐格式, 精确且高效求解了非稳态二维对流扩散反应问题.构造半离散化时的二次有限元,并系统建立全离散化的时间参数θ格式的代数系统, 通过3种范数的误差估计数值验证了黄金比例差分格式下二次有限元具备更高的计算精度和收敛阶数.本文方法为后续研究提供了一种新思路,可以通过合理选取θ值改善全离散格式对精度的影响.

