基于m 法计算桩- 土效应时m 取值对桥梁动力响应的敏感性分析

范振华，杨飞波

（西安长安大学工程设计研究院有限公司，陕西西安）

引言

m 法作为计算弹性桩水平位移及作用效用的最常用方法，其最主要的影响参数便是非岩石类土的m值，在采用m 法计算桥梁弹性桩基础的水平位移及作用效应时，如何选取非岩石类土的m 值将直接影响计算结果的准确程度。因此，本文依托实际工程，采用m 法计算桥梁桩基础在地震荷载作用下水平位移及作用效应值，分析选取不同m 值时桩基础的水平位移及作用效应，根据计算结果总结m 值对弹性桩基础水平位移及作用效应的影响程度，为今后工程设计人员采用m 法计算弹性桩基础水平位移及作用效应时选取m 值提供理论依据。

1 工程概况

某拟建人行玻璃悬索桥工程位于国家生态公园旅游区内，横跨河谷。桥梁采用单跨45 m 双塔地锚式玻璃悬索桥，主缆跨径布置为19+45+19 m，横向间距3.55 m，中跨主缆计算矢跨比为1/9，矢度f=5 m；吊杆间距顺桥向为2.5 m，横桥向为3.55 m；桥面全宽3.9 m，净宽3.0 m，桥面两端5.0 m 范围铺设125×35 mm欧洲防腐赤松木板铺装，中间区域铺设夹胶钢化玻璃；桥塔采用双柱式索塔，横断面方向为线型流畅的半椭圆形，塔柱内索鞍以下填充C40 微膨胀混凝土，塔柱下设承台，承台下设置2 根1.5 m 钻孔灌注桩，桩基为端承桩，桩端位于灰岩，其余段桩基均位于粉质黏土层。

2 计算参数

本文的主要目的是为了研究采用m 法计算弹性桩基础水平位移及作用效应时，如何选取非岩石类土m 值。因此，本文主要结合《公路桥涵地基与基础设计规范》（JTG 3363-2019）给出的非岩石类土的m 值和m0值[1]取值范围，选取不同的m 值和m0值，进行计算分析。

3 地震荷载

根据本工程地勘报告，桥位处抗震设防烈度为Ⅶ度，场地类别为Ⅱ类，地震动峰值加速度为0.10 g，基本地震动加速度反应谱特征周期为0.40 s。根据《城市桥梁抗震设计规范》（CJJ 166-2011）的规定，本桥抗震设防类别为B 类桥梁，采用反应谱法对E1 地震作用下桥梁桩基的水平位移及荷载效应进行计算分析。桥梁结构阻尼比取0.03，水平向设计加速度反应谱S 由下式（规范5.2.1）[2]确定：

式中：Tg——特征周期；T——结构自振周期；Smax——水平设计加速度反应谱最大值。η2——结构的阻尼调整系数，阻尼比为0.05时取1.0；γ——自特征周期值5 倍特征周期区段曲线衰减指数，阻尼比为0.05 时取0.9；η1——自5 倍特征周期至6s 区段直线下降段下降曲率调整系数，阻尼比为0.05 时取0.02。水平向设计基本地震加速度峰值。

根据水平向设计加速度反应谱S计算公式，计算得到的E1地震作用加速度反应谱如图1 所示。

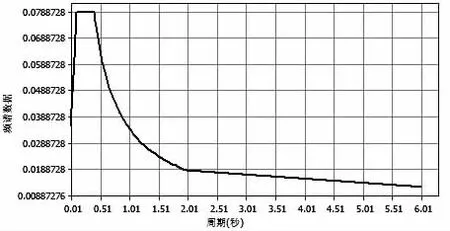
图1地震作用加速度反应谱

4 有限元模型

在本研究中，需准确模拟全桥的刚度、质量分布及阻尼特性，根据桥梁结构总体布置，本桥采用“梁格式”主梁模式，采用有限元软件Midas Civil 建立全桥空间有限元计算模型。由于本项目为双塔单跨悬索桥，没有边跨及其他相邻构筑物，在进行地震作用下的桩基水平位移及作用效应分析不计其他相邻构筑物的影响。加劲梁、桥塔、桩基、主缆及吊杆等单元选择、单元划分及边界条件模拟如下：（1） 单元选择：加劲梁、桥塔、承台、桩基采用空间梁单元模拟，主缆、吊杆采用空间只受拉桁架单元进行模拟，二期恒载按照附加质量计入。（2） 单元划分：全桥共划分662 个单元，641 个节点。（3） 边界条件模拟：在梁底支座实际位置建立节点，并将这些支座节点向下复制一个支座的高度生成支座底部节点，在新建立的梁底节点和支座底部节点间用一般弹性连接模拟支座，弹性连接初始刚度按照所采用的支座的参数计算模拟，支座底部按完全固结处理，然后通过刚性连接主梁和梁底支承节点。桥塔与承台、基桩与承台直接用主从约束（刚性连接）模拟，桩-土共同作用[3]采用弹簧（节点弹性支承）模拟，等代土弹簧刚度[4]采用表征土介质弹性值的“m”参数来计算，基桩底部用节点固定支承模拟。全桥计算模型如图2 所示。

图2 全桥空间有限元计算模型

5 计算结果与比较

5.1 水平位移

通过Midas Civil 计算分析，可得m 分别取值5 000 kN/m4、7 500 kN/m4、10 000 kN/m4时桩的水平位移，如表1 所示。不同m值结果对比，如图3 和图4所示。

表1 不同m 时地震荷载作用下桩身位移值（mm）

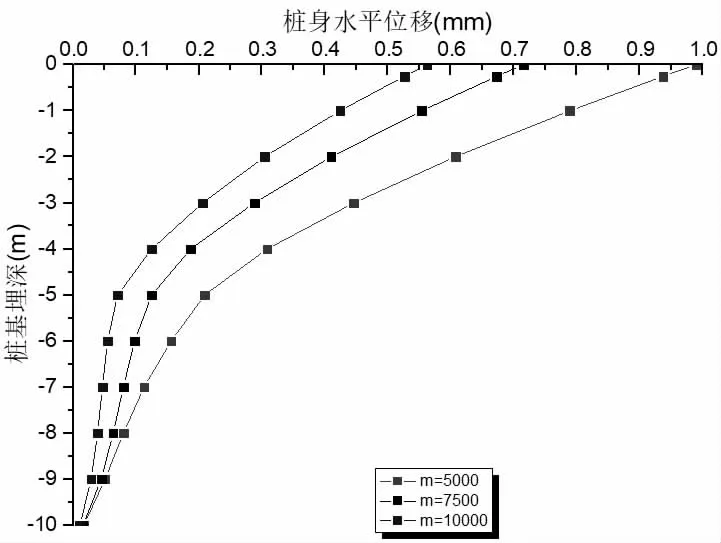
图3 桩身水平位移曲线

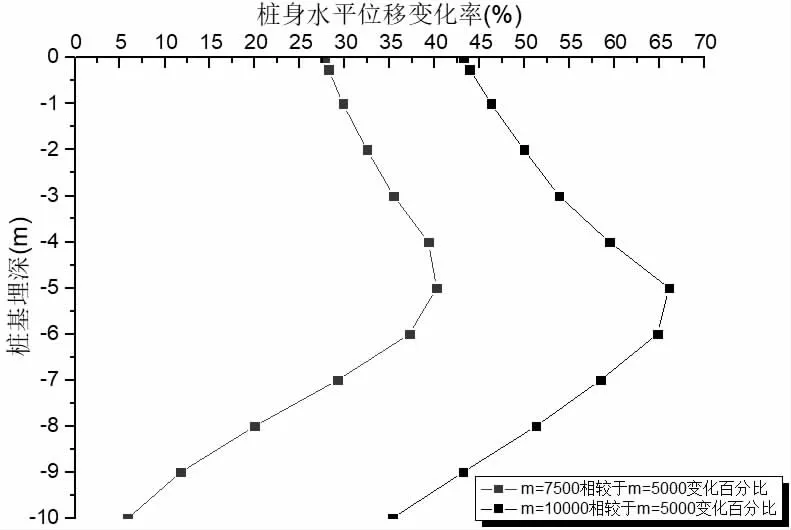
图4 桩身水平变化百分比曲线

由上述图表可知，m 值对桩身水平位移、特别是桩顶水平位移影响非常大。当m 为5 000 kN/m4时，桩顶水平位移为0.99 mm；当m 为7 500 kN/m4时，桩顶水平位移为0.72 mm，相较于m=5 000 kN/m4时，减小27.3%；当m 为10 000 kN/m4时，桩顶水平位移为0.56 mm，相较于m=5 000 kN/m4时，减小43.4%。同时，m 值对桩身水平位移的影响随着桩身埋深先增大后减小，在3～5 倍桩径范围内影响最大，当m 为7 500 kN/m4时，相较于m=5 000 kN/m4，桩身水平位移最大减小40.2%；当m 为10 000 kN/m4时，相较于m=5 000 kN/m4时，桩身水平位移最大减小66.0%。

5.2 桩身弯矩

通过Midas Civil 计算分析，可得m 分别取值5 000 kN/m4、7 500 kN/m4、10 000 kN/m4时桩身弯矩，如表2 所示。不同m 值结果对比，如图5 和图6 所示。

表2 不同m 时地震荷载作用下桩身弯矩（kN.m）

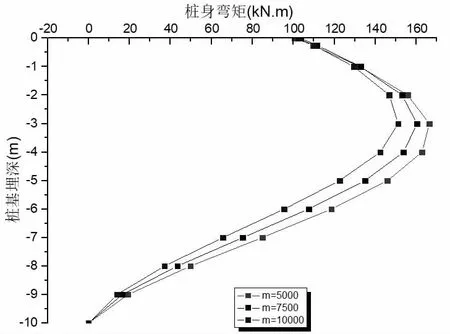
图5 桩身弯矩分布曲线

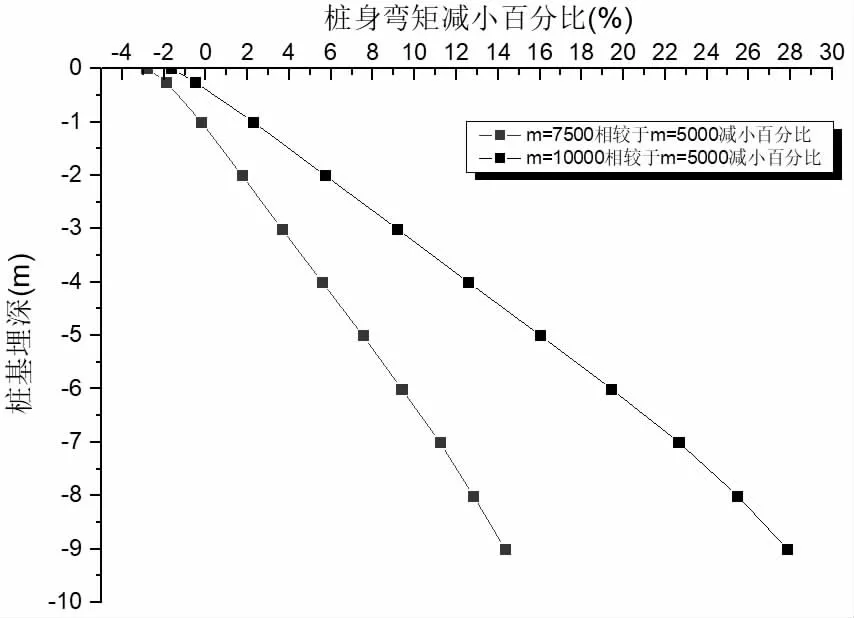
图6 桩身弯矩变化百分比曲线

由上述图表可知，m 值对弹性桩桩顶弯矩、最大弯矩位置及桩身反弯点几乎无影响，桩身最大弯矩均位于2～3 倍桩径范围内，但其对桩身弯矩最大值影响较大。当m 为5 000 kN/m4时，桩身弯矩最大值为166.3 kN·m；当m 为7 500 kN/m4时，桩身弯矩最大值为160.3 kN·m，相较于m=5 000 kN/m4时，减小3.6%；当m 为10 000 kN/m4 时，桩身弯矩最大值为151.1 kN·m，相较于m=5 000 kN/m4时，减小9.2%。同时，m 值对桩身弯矩的影响随着桩身埋深逐渐增大，当m 为7 500 kN/m4时，相较于m=5 000 kN/m4，桩身弯矩最大减小14.3%；当m 为10 000 kN/m4时，相较于m=5 000 kN/m4时，桩身弯矩最大减小27.8%。

6 结论

本文结合实际工程案例，基于m 法分析了土层不同m 值时桩基的桩身弯矩、水平位移变化情况，得到了不同m 值对桩基的桩身弯矩、水平位移的影响。得到以下结论：

（1） 计算实例表明，采用m 法计算桥梁桩基础的水平位移及作用效应时，不同的m 值对桩身的水平位移、弯矩效应值影响很大，因此工程设计人员应高度重视。

（2） 对于大部分桥梁，桩基多为常用尺寸及传统工艺，很难具备试桩资料，m 值基本都是根据规范建议的值进行选取，而规范给定的非岩石类土的m 值是范围值，仅由土的类别确定，没有考虑地形、桩的直径、刚度、直径等其它因素的影响，并且假定地面处最大位移值不应超过6 mm。设计人员在查表选取m 值时，即使是某一特定土，其m 值选取存在任意性，会严重影响桩基水平位移及荷载效应的计算精度。因此，工程设计人员在采用m 法对桥梁桩基计算分析时对于m 值的选取应更加慎重，必要时可通过土工试验确定非岩石类土的m 值。