生物阻抗谱参数提取算法研究
任朝辉,张 博
(杨凌职业技术学院,陕西咸阳)
概述
生物组织的电特性即生物领域中的“静钾动钠”概念,简单来讲,生物体内的组织、细胞在进行正常生理活动时,由大脑下达行动“指令”,这一指令表现在生物体内,就是一系列的电信号[4]。细胞在静态电位时,主要由体内的钾离子控制,而在动作电位时,主要由体内的钠离子控制,阳离子的内流或者外流导致了细胞膜两侧存在电位差,这一差值就产生了生物组织的电特性。
众所周知,细胞是构成生物的最小单位。在不同的生理及病理状况下,生物细胞具有不同的电特性,细胞膜、细胞内液、细胞外液构成单个细胞的等效电路模型[5]。基于此,生物阻抗测量得以实现。在低频电流下,激励无法穿过细胞膜,生物细胞呈介电特性;在高频电流下,激励穿过细胞膜,生物细胞呈导电特性[6]。研究生物细胞的电特性,特别是其随频率的变化特征,将有助于准确辨识生物组织的功能状态。
利用Cole-Cole 生物电阻抗特征方程可以有效的对生物阻抗参数提取和分析。查阅文献之后发现,生物阻抗参数提取多采用Cole-Cole 拟合的方式。
尽管复阻抗- 频率函数呈现出显著的非线性特性,传统的方法如梯度下降法却无法达到预期的拟合精度。非线性最小二乘法在执行拟合任务时,常常遇到无法收敛或仅能找到局部解的问题,这种现象通常是由于初始值的选择不当所导致的。此外,该方法对于等效电路拟合的适应性也存在一定问题。相比之下,遗传算法凭借其随机搜索能力,能够摆脱初始值的影响,因此在初始值估计方面表现得更为优越。本文计划采用遗传算法(GA)与非线性最小二乘法(NLS)相结合的方式(NLS-GA)进行等效电路拟合。通过非线性最小二乘程序进行迭代求解再加上遗传算法提供的参数初始值,收敛结果为最终的电路拟合参数。
1 生物阻抗谱检测方法
单个细胞在通入低频交流电时,低频电流被细胞膜阻断而无法通过,此时细胞膜处于高阻态。当不断增加激励电流的大小时,高阻态逐渐消失,此时电流可以轻松穿过[2]。图1 所示为生物细胞的三元件等效电路模型。由于细胞膜存在介电特性,所以加入一个与细胞膜并联的等效电容Cm来模拟真实的细胞状态,当电流达到一定频率时,就可以轻松穿过细胞膜,Re在这里用来模拟近似细胞外的电阻值,Ri在这里用来模拟近似细胞内的电阻值[3]。

图1 理想状态下的生物细胞三元件等效模型
通常情况下,当电极接触到细胞悬浮液时,会产生一个具有相同电量且符号相反的过剩电荷,这种现象被称为双电层(Electrical Double Layer,EDL)。为了模拟实际生物测量的环境,我们需要引入等效电阻和等效电容来构建等效电路模型,修正后的检测等效电路如图2 所示。
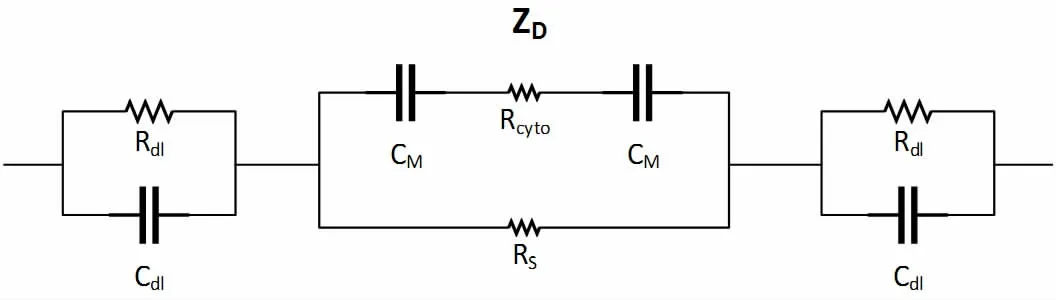
图2 细胞等效电路模型
在对等效电路进行拟合时,主要涉及到5 个待估参数作为遗传算法的决策分量,分别是:Cdl:双电层电容;Rdl:双电层电阻;CM:细胞膜电容;Rcyto:细胞质电阻;RS:细胞外液电阻,图中ZD表示细胞检测阻抗。
生物组织的复阻抗特性与频率之间的关系通过Cole-Cole 图表得以呈现。对于精确地识别和分析生物组织的电学属性,一种常见的策略是利用Cole-Cole拟合技术对阻抗谱进行分析,从而揭示出生物组织内电阻原件和电容原件的组成元素如何随着频率的变化而调整其行为模式。等效电路的Cole-Cole 模型为第四象限内的一段圆弧,圆心在第一象限。如图3 所示。
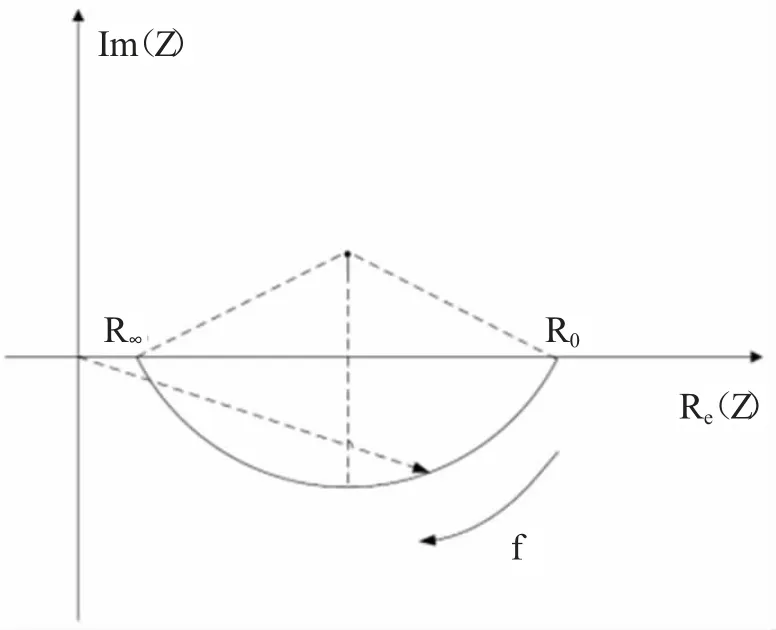
图3 Cole-Cole 等效模型
构建生物阻抗特征方程为我们提供了一个有力的理论框架,用于获取并解析生物阻抗参数,科尔拟合法多用于生物阻抗参数的提取。科尔原理作为生物阻抗谱测量的基础,其建立起来的特征方程,为生物组织的特征参数提取提供了良好助力。由于生物组织存在介电特性,此时若对生物组织外加激励电流,那么节点参数会随着激励频率的改变而发生改变,即Schwan[1]提出的生物组织测量过程中存在三种频率散射现象,如图4 所示。

图4 生物组织频率特性曲线
2 基于遗传算法的初始值估计
利用等效电路模型,我们能够构建一个包含所有元件参数作为求解变量的复阻抗- 频率响应函数模型。然而,这个模型呈现出显著的非线性特性,因此需要运用非线性最小二乘法来处理这些复杂的曲线。此外,我们还借助了遗传算法(GA)来估算初始值,从而进一步降低拟合误差。
2.1 遗传算法
阻抗参数出发点是从满足约束条件的可行解中优选出使得最符合目标函数要求的解,在此处即最小的解。除此之外,遗传算法对全局变量进行最优检索的方式在最优解拟合方面具有更大的优势,具体描述为求解目标函数极值(最小值)的数学模型:
式中:向量X=[x1,x2,...,xn]T为所要求解的拟合参数;(fx)为目标函数;U 为可行解空间。
2.2 适应度函数模型建立
在得到生物组织等效电路之后,可以根据复阻抗- 频率数学模型建立相应的遗传算法目标函数模型和适应度评价指标,在对等效电路进行拟合求解时,建立如下标函数模型:
式中:z'和z"分别为通过测量得到的阻抗谱数据的实部和虚部标准值;z'和z"分别为通过遗传算法拟合得到的实部和虚部拟合值。
寻找等效电路拟合的最优参数估计x 的过程,实际上是通过计算一系列目标函数来达到这一目的。根据公式(2),我们知道目标函数的值必须大于零,而且个体目标函数值越小,其对应的参数估计值x 就越精确,这意味着这个参数的适应程度更高。因此,我们可以将适应度函数模型定义为:
Q 的值越大,F(x)的个体适应程度越小;Q 的值越小,F(x)的个体适应程度越大。
在建立了相应的适应度评价指标后,在每次演化计算之前,对每个个体适应度进行计算,然后通过选择算子对个体进行优选。
3 非线性最小二乘拟合
最小二乘拟合的基本原理就是使得实验测量值和预测值之间的误差平方和最小,从而找到最佳函数匹配模型。非线性最小二乘问题可以定义为:
式中:x=[x1,x2,...,xn]T为需要求解的拟合参数;函数F(x)为需要求解的代价函数;F(x*)为函数预测值;a为实验测量值;e(x)为二者之差;x*为代价函数的全局最优点。若x*为局部最优点,则在x*的搜索区域δ处,满足如下条件:
3.1 目标函数模型建立
在生物阻抗谱研究领域,一旦构建了等效电路模型,我们就可以通过角频率和m 个电路元件的特性x1,x2,…,xm来描述阻抗z。具体来说,阻抗z 可以被表示为z(ω,x)的形式。为了实现生物等效电路的最小二乘拟合,我们的目标是找到m 个参数的最佳估计值,从而使得目标函数F 达到最小值,最终可建立如下目标函数模型:
3.2 高斯- 牛顿求解
对式(7)进行高斯- 牛顿求解。在对生物电阻抗谱数据拟合过程中,由于参数初始值x0l已由遗传算法给出,与预测真值之间较为接近,所以在进行高斯-牛顿求解时常把非线性误差函数转化为线性函数。令该拟合参数初始值x0l和预测真值xl的差值Δl=xl-x0l,最终通过不停迭代计算寻找函数的局部最小值,所以误差函数fRe和fIm(x)可以近似为:
雅可比矩阵JRe(x)和JIm(x)为函数fRe和fIm(x)的一阶导数,对Δl 进行求解,使得目标函数变为式(10):
为了求解目标函数极值,对F(x+Δx)进行求导,并使得F'(x+Δx)=0,可求得:

因此,对于生物阻抗谱系统而言,在建立了生物组织对应的等效电路函数模型之后,对函数模型进行高斯- 牛顿求解并设定拟合参数的初始值,就可以通过方程(11)计算出目标函数初始估计值和最优估计之差Δl。将求解结果代入下式,即可求得估算值:
在混合算法的设计中,遗传算法已经提供了足够优良的初始参数估计,且满足一定的收敛条件。迭代收敛条件定义为:
当最终结果满足最终收敛条件,当前计算所得的估计值近似等于真实值。
4 拟合实验及结果分析
为了比较非线性最小二乘法(NLS)、遗传算法(GA)以及它们的结合体——混合算法(GA-NLS)在数据拟合方面的表现,我们选择了一个特定的细胞等效电路模型作为测试对象。首先,我们构建了一个待测电路,该电路由预先确定的标准电阻和电容组成。然后,利用阻抗分析仪获取了阻抗谱的数据,并通过计算平均值来减小随机误差的影响。接下来,我们使用这三种算法对阻抗数据进行了多次处理,目的是让拟合结果具备统计学的有效性。
最后,我们分别使用这三类算法对细胞等效电路的阻抗谱数据进行了拟合,并且希望找到一个能够尽可能地使拟合数据与测量数据相匹配的拟合算法。因此,我们主要依赖于残差平方和来评估拟合算法的精确度。拟合情况对比如图5 所示。

图5 不同算法拟合效果
不同算法标拟合结果统计如表1 所示。
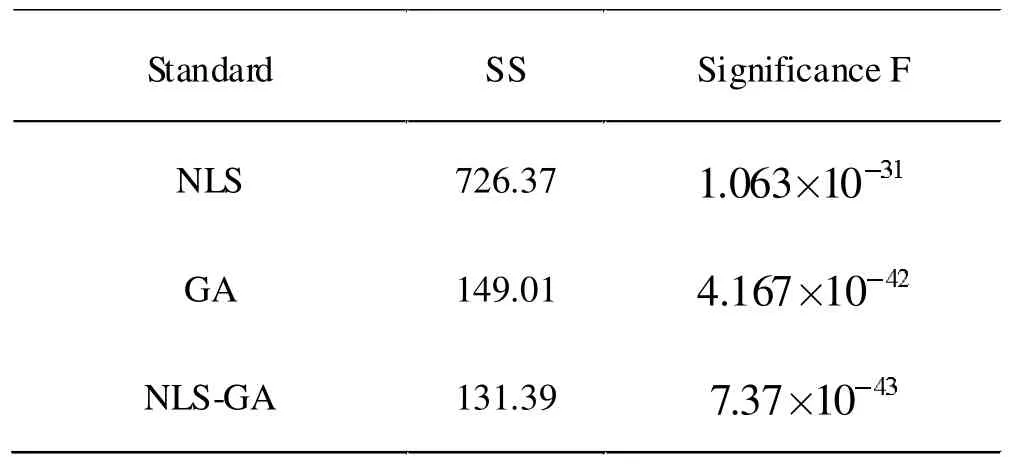
表1 不同算法拟合结果对比
从图5 可以看出,在单独使用NLS 拟合时,由于参数初始值具有随机性,存在较大的拟合误差。在单独使用GA 拟合的情况下,虽然最终的拟合结果相比于NLS 精度要高很多,但最终的拟合精度仍然要比经过进一步NLS 迭代的要小。且从表1 可以看出,NLS-GA 数据变化总量SS 最小,Significance F 的值也最小,这表明NLS-GA 的值更有意义,更贴近实际测量值。
5 结论
本文在生物组织等效模型的基础上,提出了一种阻抗谱参数提取方法,采用遗传算法(GA)提供参数初始值,结合非线性最小二乘法(NLS)迭代的混合方式(GA-NLS)进行阻抗谱参数提取。实验结果表明,NLS-GA 在等效电路拟合方面更加接近实际测量值,其所得数据更具有意义。

