基于支持向量机的陶瓷原料成分识别

郭若楠

（西安石油大学，陕西西安）

引言

SVM 是一种用途极为广泛的小样本分类器，在对数据进行二元分类的过程中开展有导师学习[1]，稀疏和稳定为其典型特征，在处理线性不可分数据的分类问题上有极为优异的解决手段[2]，在处理陶瓷原料分类中也有很好的分类效果。

1 支持向量机理论基础

SVM 同时考虑了经验风险和结构风险的最小化[3]，在解决不具有线性可分性的问题上，它是一个寻求最小化结构风险和经验风险的线性组合的过程，通过训练数量有限的训练样本，可以得到一个具有良好统计规律并且误差很小的分类器。

SVM 的稀疏性和稳定性使其具有良好的泛化能力，其思想就是将不可分的数据变换到高维空间，建立最好的分类超平面，使得空间间隔最大化，从而让数据变得线性可分，而在将输入空间变换到高维特征空间时,会增大计算量，核函数是节约计算资源和空间资源的关键。SVM 的出现有效地解决了传统算法因强调执行机器学习时经验风险最小化导致出现“过度学习”和泛化能力差的弊端。另外，SVM 因其特有优点被人们广泛应用于图像识别、模式识别和文本分类中。

SVM 主要是立足于两类问题分类中同时应用的带线性可分性最优分类面的基础上所提出的[4],如图1所示。下面内容以二分类为例，详细分析SVM 基本理念。

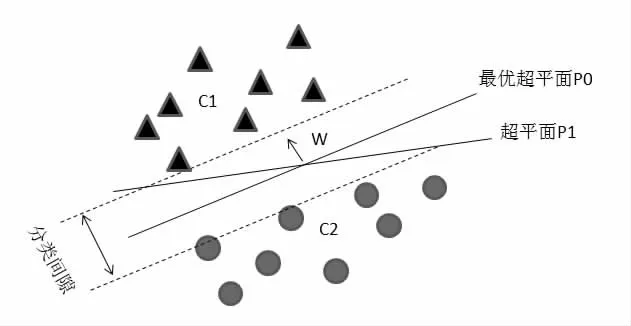
图1 最优超平面

式中：i＝1，…,N。

其约束条件是：

式中：i＝1，…,N。

得到以下拉格朗日函数：

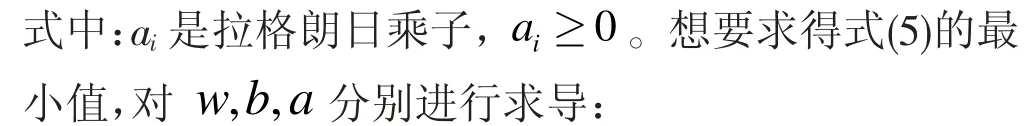
通过式(2)和式(6)达到了利用对偶原理把解决最优分类面的问题转为求解最优凸二次规划的目的，有：

约束条件是：

这样就求得了支持向量机的一般表达式。

2 核函数

2.1 核函数变换基本原理

处理非线性分类时，在输入空间中寻找到的最优分类面没有办法取得令人满意的分类效果。解决这个难题需要在输出的高维空间中映射出原空间中的非线性样本数据，同时找到高维空间中最好的超平面来实现对样本数据的线性分离，但这种方式的映射无疑使运算量大大增加。核函数的巧妙运用使得支持向量机灵活地解决了该问题。通过将N 维输入空间中的向量X 映射到高维的输出空间中，并且在高维空间中表现出线性可分性，就可以在输出空间中对样本实行线性分类，核函数转换的基本理念就是这样来的。通过观察式（7）和式（11），只与训练样本之间的点积运算xi,xj有关系。若存在一个非线性映射Φ将Rn空间样本映射到了一个更高维度的H 空间，即可表示为：

2.2 常见核函数

（1） 线性函数

（2） 径向基函数

式中：σ 是超参数，用于控制点之间的相似度。

（3） 多项式函数

式中：d 是度数，用于控制多项式函数的形状。

（4） Sigmoid 函数

式中：ɑ 是Sigmoid 函数的阈值。

基于这四个核函数形成了线性、RBF、多项式、感知四个SVM。

3 支持向量机多类分类问题

SVM 是一个二分类分类器，但在实际中有大量的多分类问题亟待解决，因此此处需要阐述一下多类分类问题的基本原理。目前学者们主要使用以下两种方法将SVM 推广至多类SVM。一种是将所有数据在一个优化公式中进行综合优化；另一种是将若干类问题分解成若干个二值分类问题。第一种想法的计算比后者的计算对于同样的数据来说要复杂得多。目前多类分类器有一对多、一对一和有向无环图SVM 三种。

4 基于支持向量机的陶瓷原料分类实验

本文采用《陶瓷工艺学》一书中我国常用的陶瓷原料主要化学组成作为原始数据,为了测试SVM 算法的分类效果，所有108 种陶瓷原料数据进行归一化处理并采用五折交叉验证，对陶瓷原料类别分别采用线性核和高斯核支持向量机对样本数据进行分类。首先对SVM 分类算法进行参数设置，分别采用线性核和高斯核创建SVM 分类器。通过训练集中的78 组陶瓷原料数据有效对模型进行训练，再面向测试集的30组陶瓷原料数据完成分类预测。

将SVM 线性核惩罚系数默认设置为1，利用SVM 线性核对陶瓷原料进行预判，得到测试集各样本预测分类情况与每种类别识别正确率如图2 和图3所示。除此之外，还设计了混淆矩阵用于对陶瓷原料分类模型的准确性进行监测和评估，如图4 所示，图中矩阵的每一列表示每一个类的预测结果，矩阵的每一行代表被分类数据的真实属性。

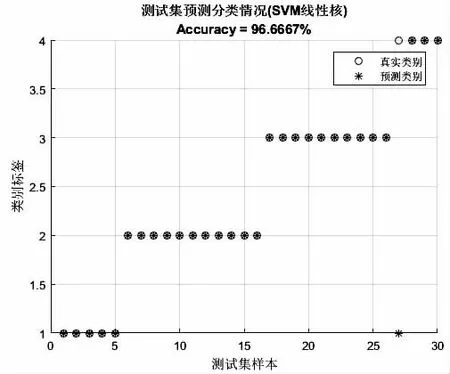
图2 SVM 线性核预测分类情况

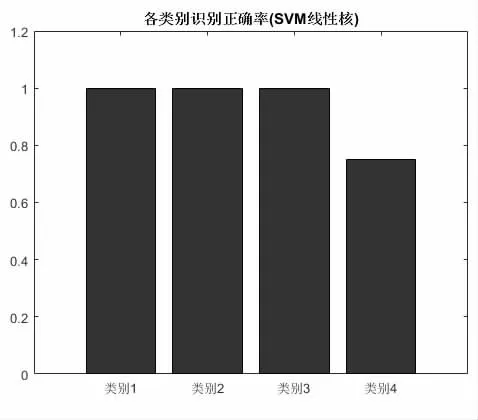
图3 SVM 线性核各类别识别正确率

从实验结果可得，SVM 线性核算法对陶瓷原料预测正确率较高，SVM 线性核预测结果见表1。

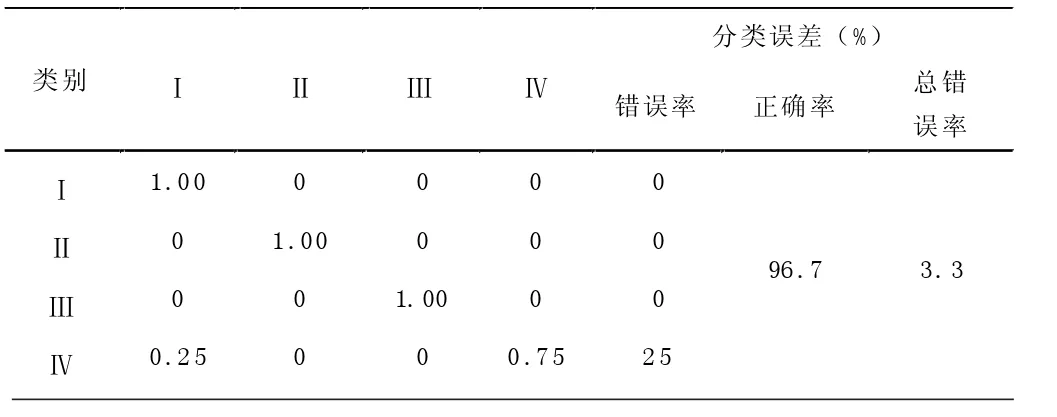
表1 SVM 线性核分类结果

由表1 可得，Ⅰ类、Ⅱ类和Ⅲ类模型预测结果正确率均为100%；对于Ⅳ类陶瓷原料而言，有25%识别成了Ⅰ类，其余识别正确，整体预测准确率是96.7%。

5 结论

陶瓷原料种类丰富，每种原料成分组成相当复杂，但化学含量是可方便测量的，因此将其定为识别因素，保证了研究的合理性与科学性。本文使用的线性核支持向量机预测准确率为96.7%，其分类结果足以解决大部分陶瓷材料分类问题，结果合理，方法实用，为陶瓷原料分类和实际选取带来诸多便捷，对实际生产意义重大。