基于蚁群算法的纯电动汽车路径规划研究

李佳燕，方存光，槐崇飞

(沈阳理工大学汽车与交通学院，沈阳 110159)

近年来，随着全球气候变暖，能源损耗和环境污染等问题不断加剧，零尾气排放的纯电动汽车成为绿色出行的最佳选择，然而，纯电动汽车在能量储存、充电时间、续航里程方面的短板将对用户的出行带来一定影响[1]。 因此，合理规划出行路径对缓解出行焦虑具有重要意义。

纯电动汽车的路径规划涉及电池容量、充电桩布局、车辆行驶能耗、出行时间、行驶里程等主客观因素，许多国内外学者基于算法从降低出行成本及提高出行效率的角度出发开展路径规划。文献[2]运用A*算法求解时间、能耗双变量最优充电路径，但其搜索时间随路径的复杂而增加；文献[3]提出了经典路径规划Dijkstra 算法，但不能解决纯电动汽车能量回收时的负权边问题。 文献[4]提出了一种基于蚁群算法的电动汽车路线优化问题的分布式算法，为电动车司机提供距离最短的充电路径；文献[5]采用蚁群算法求解双目标路径，验证了此算法易于修改以解决两个及以上的目标路径；文献[6]验证了蚁群算法具有较强鲁棒性、优良分布式计算等优点，并且在求解路径规划问题时具有较强的全局搜索能力。 因此，本文基于已知输入数据信息，采用离线蚁群算法开展路径规划。

文献[7]基于车辆负载、行驶距离和速度建立电能消耗模型并应用自适应粒子群优化算法进行路径规划，但是未考虑中途充电的情况。 文献[8]基于“车-路-网”信息的融合对电动汽车充电路径进行了优化，但未考虑交通信息的动态特征。文献[4]考虑了节点坡度和海拔对电耗的影响，但忽略了交通拥堵情况下的路径规划。

综上所述，目前国内外对纯电动汽车路径规划的研究取得了一定成果，但未全面考虑电动汽车充电需求、交通状态、地形等因素的影响，所规划路径缺乏整体性和系统性。 因此，本文根据路网节点位置、海拔高度、充电站位置等信息建立沈阳市20 km×20 km 区域内道路拓扑结构，考虑交通动态性及速度时变性，基于车辆充电需求、行驶距离、行驶时间、行驶能耗、空调等附件能耗建立纯电动汽车多目标路径函数，采用蚁群算法开展路径规划。

1 道路拓扑结构建模

通过网络地图选取实际道路，收集路网节点位置与海拔、充电站位置等重要信息，并对其进行数据统计及分析，采用图论分析法[9]建立路网数学模型为

式中:G表示路网；V表示路网节点集合；n表示路网中的节点总数；E表示路网所有路段集合；W表示路段权值集合，本文路段表示的权值为距离、时间和能耗；S表示路网充电站节点的集合，且S∈V；m为充电站节点总数。

设图G有n个节点分布，则邻边权值矩阵[10]R＝(rij)n×n，其中

因此，邻边矩阵E可表示为

式中∞表示vi和vj之间不存在连接路段。

本文以沈阳市20 km ×20 km 的某区域内实际交通路网作为研究对象并采集该区域路网信息，共取60 个路网节点，三座充电站，即S1、S2、S3，所在位置为v10、v20、v34，起点位于v11，终点位于v55，路网拓扑结构示意如图1 所示。

图1 路网拓扑结构示意图Fig.1 Schematic diagram of road topological structure

研究时间选取沈阳市夏季下午两点，所选时刻存在三种交通拥堵情况，如图2 所示。

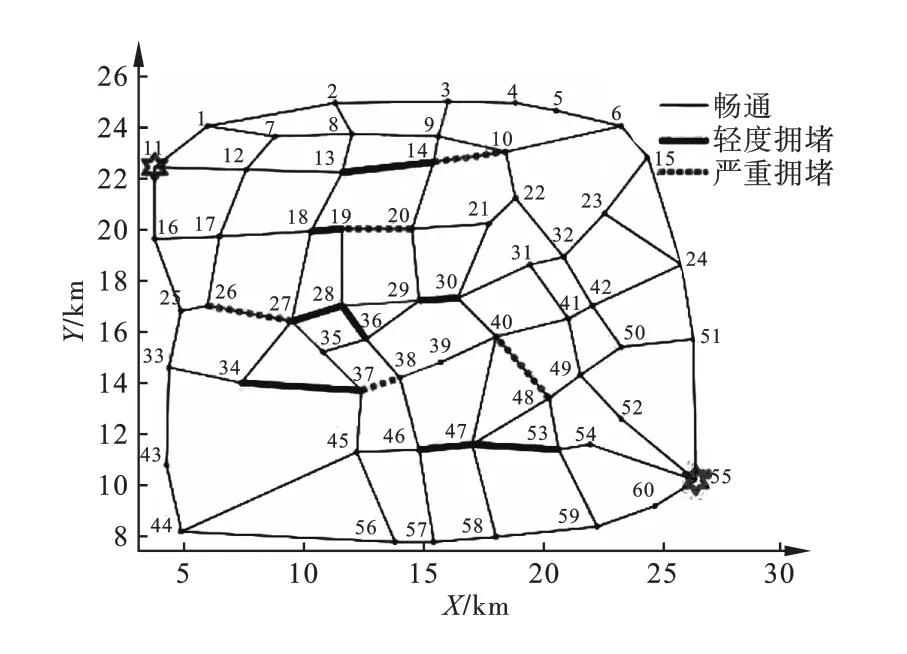
图2 交通路况信息示意图Fig.2 Diagram of traffic conditions informations

所选路段为主干路，路段平均速度对应拥堵等级划分如表1 所示，表中1 级为交通畅通、2 级为轻度拥堵、3 级为严重拥堵。

表1 路段平均速度对应拥堵等级划分Table 1 Average speed and congestion level of road section

根据图2 中拥堵情况选取表1 中对应的平均速度进行动态规划:畅通时取50 km/h；轻度拥堵时取30 km/h；严重拥堵时取10 km/h。

基于文献[11]中速度与坡度的关系式，本文考虑了速度随坡度动态变化的情况，即电动汽车的总功耗与道路倾角呈正相关，耗电量随着上坡的倾斜角增加而增加，随着下坡的倾斜角减少而减少。

在上述基础上以距离、时间及能耗作为出行的三个目标，并以此开展多目标路径规划研究。

2 多目标路径函数建模

建立多目标路径函数之前，首先根据电动汽车用户不同的出行需求建立对应函数模型。

2.1 行程距离目标建模

行程总距离函数为

式中:dij表示路段距离权值；xij为0 -1 约束变量，若车辆经过路段vij，则xij值为1，否则xij值为0。

2.2 行程时间目标建模

考虑充电站充电车辆小于充电站充电设备，则无排队等待时间，由此电动汽车行程总时间Tall包含以下两个部分:起点至终点各路段的行驶时间Td、充电时间Tc。 计算公式为

式中:表示从节点i行驶至节点j的速度；Eb为电池容量；表示电动汽车在充电站Sa(a＝1，2，3)处开始充电的剩余电量；为电动汽车到达充电站补充电量时间，为保护电池，本文中的充电时间指电动汽车到达充电站Sa后从剩余电量充至荷电状态为80%时所需时间；表示充电站的充电功率；ηe为充电效率。

2.3 纯电动汽车能耗目标建模

在纯电动汽车能耗模型建立之前，首先根据能耗来源的不同将其分为三类[12]:第一类为行驶能耗，即克服滚动、加速、坡度、空气四种阻力实现驱动行驶的能耗，同时考虑电动汽车制动能耗回收；第二类为空调能耗；第三类为其余附件能耗。基于上述分析，本文建立纯电动汽车模型为

式中:X1、X2为0-1约束变量，即对应耗电设备开启为1，否则为0；Eall为总的能耗；表示行驶能耗；表示空调能耗；表示其他附件的能耗。

2.3.1 行驶能耗建模

根据汽车理论[13]可知，在水平路面上汽车行驶的总阻力为

式中:Ff、Fi、Fw、Fj分别为汽车行驶时的滚动阻力、坡度阻力、空气阻力、加速阻力；m表示车辆总质量；CD表示空气阻力系数；ρ为空气密度；Af为电动汽车迎风面积；θ表示坡面角度；g为重力加速度；v'为行驶速度；fr为滚动阻力系数。

在汽车行驶过程中，由于汽车驱动力与行驶阻力为平衡力，由此汽车的行驶驱动功率为

考虑电机的输出功率经机械传动的过程中会造成损失，将上述功率改为

式中:η1为机械传动效率；η2为电动机工作效率；η3为电池效率。 考虑电动汽车的再生制动可以将部分电能恢复并存储至电池中，其再生制动功率为

式中k是再生制动因子。

因此，整个路段包括电动汽车行驶电耗及再生制动回收电耗[12]，结合上述公式得到节点i行驶至节点j的行驶能耗为

式中sd、sc分别表示行驶能耗及制动回收的路段占比，且0≤sd＜1，0≤sc＜1，sd+sc＝1。

为了计算便捷，忽略加减速对能耗的影响，将节点i行驶至节点j经过路段的能耗简化为

式中E1ij从车辆行驶速度和路网距离获取相关数据，E2ij由地形所决定。

2.3.2 附件设备能耗建模

1)空调能耗

电动汽车附件耗能设备的使用对续驶里程带来较大的影响，而空调在附件设备能耗占比约60%。 因此，有必要建立空调模型以进一步探究车辆路径规划问题。 首先基于空调的热负荷构成热平衡方程[14]为

式中:H为汽车整车热负荷；HO为车身不透明结构传入的热量；HC为玻璃以对流方式传入的热量；HR为玻璃以辐射方式传入的热量；HP为车内人员散发的热量；HV为车内泄漏及补充新风带入的热量；HM为空调电气设备造成的热量(取50 W)。 根据各类热负荷与设定温度的相关性简化公式为

式中:HA表示车身热传导负荷；U表示车身综合的传热系数；Ab表示车身面积；Tset表示车内空调设定温度；Tsrd表示外部温度；r表示车内人数；ω表示群集系数，即(成年男子人数+成年女子人数×85% +小孩人数×75%)/总人数，以成年男子散热量116 W 为基础；Y表示人均所需换气量，取每人20 m3/h；Δh表示车内外空气焓差，当车外35 ℃、车内25 ℃时，Δh取20。

综上，在空调热负荷状态下，维持当前车内温度所需消耗空调功率Pair及能耗公式为

式中γ为热负荷传递系数；δ为压缩机效率。

2)其余能耗附件

除空调耗能以外，附件耗电设备还有动力转向系统、导航系统、音响、喇叭、车灯等，计算能耗公式为

式中pmedia为其余附件功率。

2.4 多目标路径规划函数建模

2.4.1 目标函数

以上文各目标函数为基础建立多目标路径函数[15]为

式中α0、β0、γ0为系数，分别代表出行用户对距离、时间及能耗需求的重要程度，其系数越大表示对应目标需求越高，且α0+β0+γ0＝1。

此外，由于距离、时间及能耗三个研究目标具有不同的单位、量纲和数量级，当求解多目标问题时，若直接相加求和，会突出数值较大的因素在目标函数中的作用。 因此对其采用标准化处理[16]消除三者之间的量纲关系，构建目标函数为

式中Ld，min、Ld，max、Tall，min、Tall，max、Eall，min、Eall，max分别表示距离、时间、能耗的最小值和最大值。

2.4.2 约束条件

1)路径选择约束

式中:O为起点；D为目的地。 路径选择约束在于规定电动汽车经过的节点，即当节点作为起点，则仅存在xij＝1，xji＝0；若i作为中间节点，则存在节点j1、j2，使xj1i＝1、xij2＝1；若i作为终点，则仅存在xij＝0，xji＝1。

2)剩余电量约束

到达充电站剩余电量约束为

到达目的地剩余电量约束为

式中:b0为电动汽车初始电量；I表示车辆从起点至充电站途径节点的集合；Z表示车辆从充电站至终点途径节点的集合，且I、Z∈V。 为防止车辆中途抛锚，在抵达充电站及终点时，其剩余电量须高于电动汽车电池电量下限，本文中约束(26)和(27)下限设置为10%。

3)车辆充电站充电约束

当车辆抵达充电站时小于80%Eb的情况下将会有充电需求，否则无充电需求。

3 基于蚁群算法的路径规划

蚁群算法在搜索最优路径问题上具有较强能力，且运算效率较高，其过程如下。

1)初始化

N表示迭代次数，初始化N＝0；Nmax表示最大迭代次数；M表示蚂蚁数量。 以等量信息素赋值在各个路段上，并将所有蚂蚁放于起点处，编入二维禁忌表，初始化为空，保证在正常行驶过程中电动汽车不会重复遍历节点。

2)选择前往节点策略

蚂蚁的任务是从起点出发经过若干个路口到达终点搜索出一条路径，因此将M只蚂蚁均置于起点处按概率函数进行各自搜索任务，并逐步获得目标路径。 设当前蚂蚁k由点i向点j不断移动，用lk表示未访问节点集合，若集合为空则终止此次搜索，否则按以下概率选择前往下一节点。

式中:表示当前节点i的蚂蚁k下一步选择节点j的概率；B表示优化的目标个数，本文B为3；(N)表示不同优化目标b在第N轮中蚂蚁将要从节点i到下一个相邻节点j的时刻该路段上已有的信息素浓度；α表示信息启发式因子，反映蚂蚁之间在选择路段时相互影响的程度；β为期望启发式因子，反映信息启发式因子的重要程度；φij(N)为启发函数，距离、时间及能耗目标的启发函数表达式为

按照式(28)、式(29)前往下一相邻节点j，若该节点满足约束条件则将其添加至禁忌表，若不满足则重新选择下一节点。

3)信息素浓度的更新

信息素更新是为了更快搜索出目标路径，加强当前所搜索最优路径上的信息素浓度，同时减弱其他路径上的信息素浓度，信息素按以下规则更新。

式中:ρ表示信息素挥发系数，取值范围为(0，1)，则1 -ρ为挥发后留下来的变量；各路段τij(0)均一致，Δτij(N)表示本次迭代中在路段vij上增加的信息素值，Δτij(0) ＝0；Δ(N)表示本次迭代中的第k只蚂蚁在路段vij上增加的信息素，若第k只蚂蚁在本次循环中经过路段vij，则Δ(N) ＝Q/Ck，否则为0，其中Q表示信息素强度，Ck表示本次循环中第k只蚂蚁搜索路径搜索成本，即距离、时间或综合因素下的成本。

综上所述，蚁群算法解决电动汽车路径规划问题的流程如图3 所示。

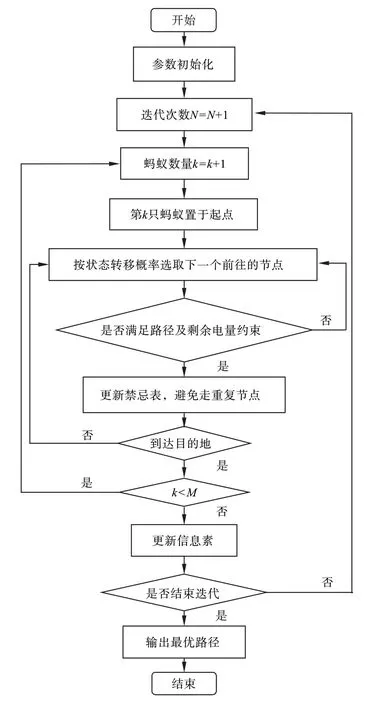
图3 电动汽车路径规划的流程图Fig.3 Flowchart of EV charging path planning

4 数值仿真

4.1 仿真条件

4.1.1 纯电动汽车相关参数确定

空调能耗参数设置:研究时间选取沈阳市夏季下午的两点，测得Tset为25 ℃，Tsrd为35 ℃，车内2 名成年男人、2 名成年女人、1 名小孩，ω为0.89。 同时，根据所研究车型Ab取16.17 m2，U取5.39，γ取0.6，δ取0.89，得到pair为1.4 kW。pmedia由以下主要附件功率组成，具体数值为:电动助力转向器200 W；单只大灯(远/近光)60 W；喇叭5 ～10 W；导航70 W；音响100 W；雨刮50 W。

车辆相关参数见表2 所示。

表2 纯电动汽车参数表Table 2 Electric vehicle parameters

此外，本文车辆电池容量Eb为30 kWh，由前文约束可知不能小于10%Eb，即3 kW，假设b0为50%Eb，可到达三个充电站。 中途充电均选择快充模式，其为60 kW，ηe为0.9。

4.1.2 蚁群算法参数确定

相关参数设置如下:信息启发因子α＝2、期望启发因子β＝3、信息挥发因子ρ＝0.2、信息素常量Q＝10、蚂蚁数量M＝90、最大迭代次数N＝200。

4.2 路径规划分析

情况1:在考虑交通畅通和行驶速度时变性的情况下，根据不同电动汽车用户的出行需求不同，对文中式(23)中α0、β0、γ0三个权重赋值，赋值数据如表3 所示，其中三个目标A1、A2、A3 分别为目标距离最短、目标时间最少、目标能耗最少。

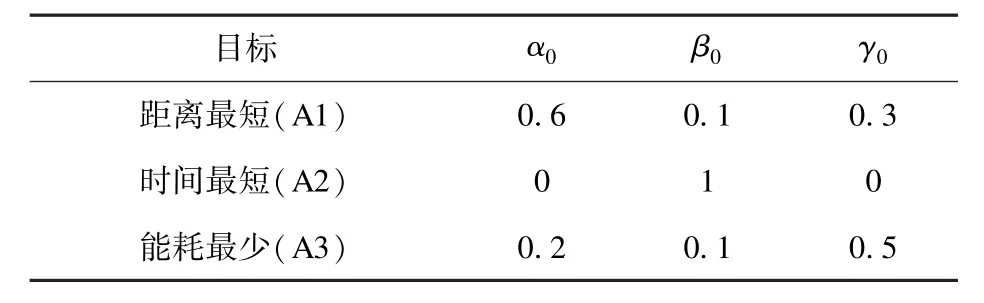
表3 三种目标参数设置Table 3 Three target parameters settings

本文还考虑了交通拥堵情况[17]及电动汽车的充电需求。 因此在上述仿真条件基础上再分三种情况进行讨论:

情况2:不考虑电动汽车充电需求，考虑道路拥堵状况；情况3:考虑电动汽车充电需求，不考虑道路拥堵状况；情况4:考虑电动汽车充电需求，同时也考虑道路拥堵状况。

考虑道路拥堵情况下对时间目标路径影响较大，因此针对情况2 和情况4 仅规划时间最短目标路径。 将情况2 条件下，仍选择情况1 规划的时间路径结果记为B2，将情况2 条件下重新规划出最短时间记为B2'；在情况4 条件下仍选择情况3 对应时间路径记为C2，重新规划后记为C2'。

4.3 多目标路径规划结果分析

基于蚁群算法并利用Matlab 软件进行数值仿真，从而得到各目标规划路径。

1)情况1 规划结果:仿真结果对比如表4 所示，距离最短为30.7 km，时间最短为0.616 6 h，能耗最少为5.305 6 kWh，对应不同出行路径如图4 所示。

表4 情况1 路径规划结果对比Table 4 Comparison of path planning results in case 1

图4 道路畅通优选路径Fig.4 Preferred path for road accessibility

2)情况2 规划结果:在交通拥堵情况下若仍选择上述图4 中的时间最短路径，得到结果如表5所示，其中目标耗时1.092 4 h，相比情况1 的A2目标增加了0.475 8 h，因此重新规划出目标，耗时为0.665 4 h，相比B2 时间缩短了0.427 h。 情况2 重新规划的优选时间路径与情况1 道路畅通条件下的A2 目标对比如图5 所示，可见，动态交通对路径规划影响较大。

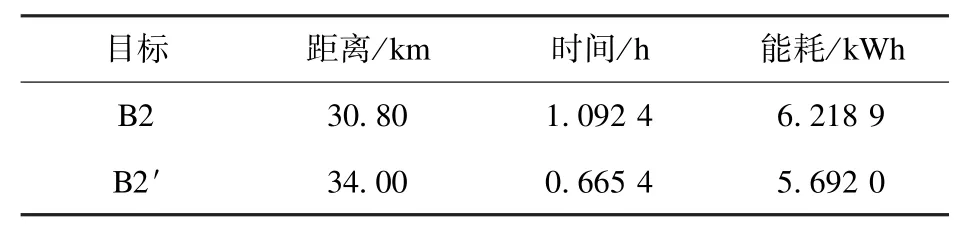
表5 情况2 路径规划结果对比Table 5 Comparison of path planning results in case 2

图5 道路畅通与拥堵优选路径对比Fig.5 Comparison of preferred paths for smooth roads and the congestion

3)情况3 规划结果:仿真结果对比如表6 所示，经过充电站S2距离最短为31.30 km，经过充电站S3时间最短为0.793 5 h，经过充电站S1能耗最少为5.346 5 kWh，对应不同出行路径如图6所示。

表6 情况3 充电路径规划结果对比Table 6 Comparison of charging path planning results in case 3

图6 道路畅通优选充电路径Fig.6 Preferred charging path with smooth road access

4)情况4 规划结果:在交通拥堵情况下若仍选择上述图6 中的时间最短充电路径，得到结果如表7 中C2 所示，耗时均增加。 因此在拥堵路况下重新规划出经过三个充电站的时间最短充电路径，对应数据见表7 中目标C2'所示。 以经过充电站S3的路径为例，其对应目标耗时为1.092 4 h，相比情况3 的A2 目标增加了0.266 4 h， 因此重新规划出目标，耗时为0.870 4 h，相比时间缩短了0.189 5 h，情况3 的A2 目标与情况4 重新规划路径对比如图7 所示。 通过表7 的数据对比可知，在拥堵情况下经过S1充电站的充电耗时最短，耗时为0.832 9 h。

表7 充电路径规划结果对比Table 7 Comparison of charging path planning results

图7 道路畅通与拥堵优选充电路径对比Fig.7 Comparison of preferred charging paths for smooth roads and the congestion

5 结论

1)现实的交通环境是动态变化的复杂系统，静态路网研究并不能真实反映路网的实况，因此本文提出了一种综合考虑交通动态性及速度时变性的纯电动汽车路径规划方法。

2)全面考虑了纯电动汽车行驶能耗、制动能量回收、空调及其它附件设备能耗，建立了电动汽车路径规划的能耗模型，同时结合时间、距离函数模型建立了多目标路径函数模型。

3)根据电动汽车用户不同的出行目标，基于蚁群算法规划出对应目标的优选路径，结果表明，所提路径规划方法可为纯电动汽车用户提供合理且多样性的出行选择，缓解出行焦虑。