基于贪心算法的无人机纯方位无源定位
祁晨彬,蔡依蝶,陈建林,王 洁
(台州学院电子与信息工程学院,浙江 临海 317000)
0 引言
无人机的有源定位原理是:由一个终端向外部信号源发射信号,当外部信号源定位后,再将定位信息发送回该终端。无源定位原理是:观测站不主动发射信号,而是通过接收目标辐射源或散射无线电信号来估计目标的位置[1]。对于静态目标,常见的无源定位方式是通过测量和计算信号发射与接收到达的时间差[2]来进行定位的;对于移动物体的无源定位,现有研究的主要对象是在海中航行的船只[3],其信号源静止、位置信息已知且无偏差。而在无人机的实际运用中,发射信号的无人机位置常常未知或已知但不精确。目前国内外常用的无源定位技术有:到达角定位技术[4];到达时间定位技术[5];到达频差定位技术[6];到达时间差定位技术[7]。
纯方位无源定位是指在不使用向外发射信号设备的情况下,同时发射信号的设备不具备接收信号的能力,仅利用被动接收信号的无人机接收到的角度信息对该无人机进行定位[8]。它具有保密性好、安全性高、距离远、隐蔽性强、抗干扰能力强、探测距离远等优点。
由于纯方位无源定位技术所用信息单一,对于高精度的定位实现较困难,特别是三维空间中移动物体的定位。徐勇[9]建立了双站无源定位模型,通过采用最小二乘法的方式来实现对目标距离的有效估计。王本才等[10]在多站纯方位无源定位算法的研究进展中指出:最小二乘算法、最大似然算法及扩展卡尔曼滤波算法等经典的算法仍存在不足,虽然其较先前的研究有了一定的进展,但依旧没有实现发射信号的无人机位置未知或已知但不精确情况下的有效定位。
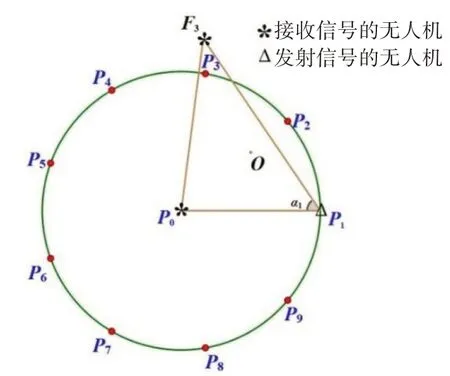
本文以全国大学生数学建模竞赛赛题为背景,考虑由9 架无人机(编号F1~F9)近似均匀分布在某一圆周上,1 架无人机(编号F0)位于圆心的圆形编队,在该圆上调整9 架无人机的位置直至使其真正均匀分布。已知纯方位无源定位条件是:被动接收信号的无人机所接收到的角度信息为该无人机与任意两架发射信号的无人机的夹角。例如:被动接收信号的无人机F3 接收到F0,F1,F5 发射的角度信息α1,α2,α3,记F0~F9分别表示无人机F0~F9 所在位置,如图1 所示。本文拟建立基于贪心算法思想的纯方位无源定位无人机的模型,调整该模型相应的参数,使其适用于圆形编队。结果表明,纯方位无源定位模型至少使用3 架信号发射无人机才可对多架无人机进行有效定位。
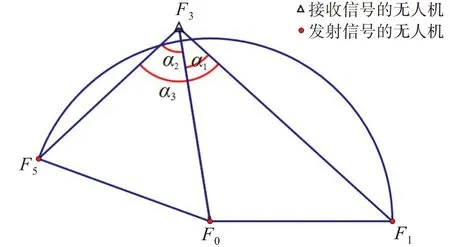
图1 被观测无人机接收到的方向信息示意图
1 模型建立和求解
由于无人机自身可以感应高度信息,即可自动调整所有无人机至同一高度,因此,文中仅考虑二维平面中对被动接收信号的无人机的定位。
1.1 基本假设
假设1:将无人机视为质点,不考虑其朝向、体积等因素对定位准确度的影响。
假设2:忽略无人机在运动过程中产生的扰动对信号接收的影响。
假设3:在运动过程中,不考虑调整所需时间,仅考虑某一时刻各个无人机的位置。
1.2 无人机纯方位无源定位模型
无人机纯方位无源定位模型是指由编队中某几架无人机发射信号,其余无人机被动接收信号,从中提取出方向信息进行定位、调整无人机位置的模型,可分为信息全已知模型和信息部分已知模型。
1.2.1 发射信号的无人机信息全已知模型
全已知表示发射信号的无人机位置无偏差且编号已知。对此我们建立被动接收信号的无人机的定位模型,由位于圆心的无人机(F0)和编队中另外两架无人机发射信号,从而调整其余位置略有偏差的被动接收信号的无人机。
设F0 为已知位置的一架无人机,F1 和F5 为另外两架发射信号的无人机。3 架无人机构成以F0为圆心、R为半径的圆,且F1,F5均在该圆上。该圆所处平面内有一点P,P指代其余待定位的无人机,将P分别与F0,F1,F5相连接,分别标记∠F0PF1,∠F0PF5,∠F1PF5为α1,α2,α3。若α3>90°,则P在弧F0F1的劣弧附近;反之,P在优弧附近。仅考虑P与F0和F1时,由于线段F0F1及其对应角α1已知,利用虚拟轨迹算法作出P点的运动轨迹(如图2 所示),不难发现P的运动轨迹为一段圆弧。

图2 仅考虑点P、F0 和F1 时P 点的运动轨迹图
设F1和F0之间的直线距离为R,且α1已知。当△F0PF1为以α1为顶角的等腰三角形时,利用等腰三角形三线合一以及同弧所对应的圆心角是圆周角的两倍的性质得出:
同理,在仅考虑P、F0和F5时,可确定P在以r2为半径的圆O2上运动。结合阿波罗尼斯圆[11]的思想,计算出两圆交点坐标,即P和F0的坐标;再结合圆的性质以及余弦公式,则可计算出P的极坐标。
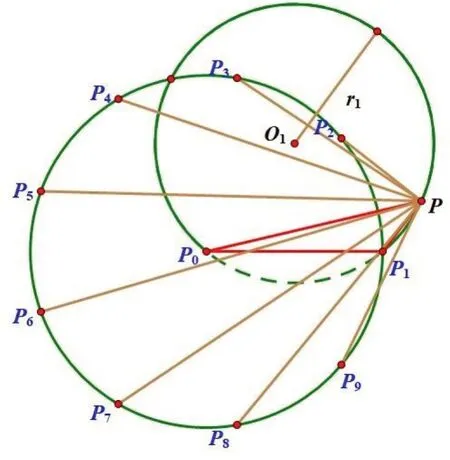
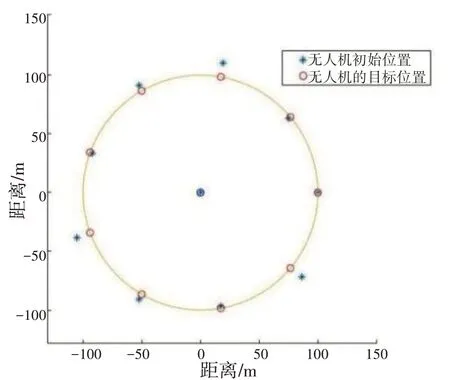
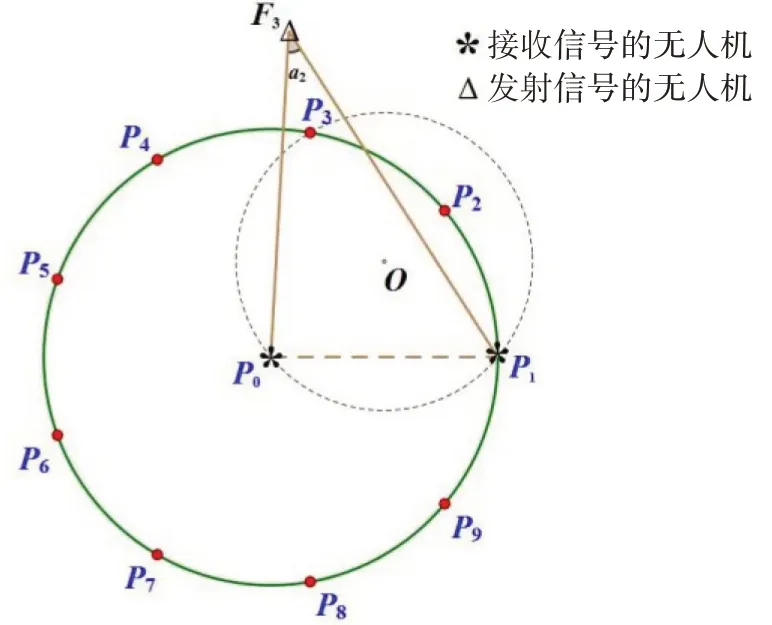
以F0为极点,射线F0F1为极轴,长度单位为m,角度单位为(°),逆时针方向为正方向建立一个极坐标系。F0的极坐标为(0,0),F1的极坐标为(R,0)。由于圆上的9 架无人机是均匀分布且发射信号的无人机位置准确,则无人机F5 的极坐标为(R,160°)。由于圆相对于任意的直径对称,可假设P在弧F1F0F5的优弧附近;若P在弧F1F0F5的劣弧附近,只需将最终所求得的位置坐标关于射线F0F1对称,Fm和Fn(其中m 图3 被动接收信号的无人机定位图 为了计算简便,以F0为坐标原点,直线F0F1方向为x轴,其垂直方向为y轴建立直角坐标系。首先,计算出圆心O1和O2的极坐标: 利用极坐标转直角坐标公式[12],计算出圆心O1和O2的直角坐标如下: 利用式(5)和式(6),计算出圆方程如下: 由于(0,0)为无人机F0 的坐标,解得点P的直角坐标为 因此,可以将上述方法推广到信号发射无人机Fm和Fn,建立被动信号无人机的定位,以F0为极点,射线F0Fm为极轴,长度单位为m,角度单位为(°),逆时针方向为正方向建立一个极坐标系。无人机F0 的极坐标为(0,0),无人机Fm的极坐标为(R,0),无人机Fn的坐标为(R,40°(n-m))。经计算得,点P的极坐标依旧为()。 1.2.2 发射信号的无人机信息部分已知模型 部分已知模型是指若发射信号的无人机位置无偏差,某位置略有偏差的无人机除了接收到编号为F0 和F1 的无人机发射的信号,还接收到编队中若干编号未知(即位置未知)的无人机发射的信号,需确定发射信号无人机架数以及对位置偏差的无人机进行调整。 已知F0和F1的坐标及其对应角∠F0PF1=α的大小,即可确定点P的运动轨迹是以O1为圆心,r1为半径的圆弧。由于O1F0=O1F1=r1,则可确定不论角α如何变化,圆心O1始终在线段F0F1的中垂线上。假设编号及位置信息未知的信号发射无人机有i(i≤7)架,则点P处共可以收到i+ 1 个以射线PF0为边的角度信号。将接收到除了α以外的角,按角度从小到大排列,依次标记为α1,α2,…,αi。令无人机F0所在位置为圆心P0,无人机F1所在位置为P1,逆时针方向标记无偏差时各无人机所对应的位置(如图4 所示)为Pj(j=2,3,…,9) 关于射线P0P1上下对称,即P2和P9对称,P3和P8对称,P4和P7对称,P5和P6对称。 图4 T 时刻∠P0PPj示意图 由于发射信号的无人机只能确定F1 和F0 的编号及位置信息,不能确定其余发射信号的无人机的位置,即其余发射信号的无人机可能处于Pj(j= 2,3,…,9)的任意点。假设仅增加一架发射信号的无人机,被动接收信号的无人机接收到3 个方向信号,分别为α,α1,α+α1。此时Pj中任意一点作为信号发射点,都可以在圆O1上找到一点P,使得∠P0PPj=α1。由此可以说明无人机信息部分已知时,仅3 架无人机不能进行有效定位。 保持α不变,即保持点P在圆弧上运动。连接PPj,记录在点P的运动过程中∠PPjP0实时变化情况。当α= 70.36°时,点P运动过程中∠PPjP0的实时变化情况如表1 所示。 表1 α=70.36°时点P 运动过程中∠PPjP0 实时变化情况表单位:(°) 若在F0 和F1 的基础上再增加i架无人机,可以对点P进行有效定位。相当于在某时刻T随机取∠1~∠8 中的i个角度信息A={α1,α2,…,αi};同样,在T´ 时刻随机取∠1~∠8 中的i个角度信息A´ ={α1´,α2´,…,αi´}。当且仅当T=T´时,使得A=A´,那么i个角度信息可以唯一确定圆O1上一点P,也就是说至少还需要增加imin架发射信号的无人机,才可以实现被动接收信号的无人机的有效定位。 为减少运算次数、优化算法,对上述数据进行以下处理:比较1~n时刻中任意两个时刻的角度数据,记录下这两个时刻8 个角中角度相同的个数N;找出任意时刻任意组合下具有最多相同角度的个数Nmax,其中,Nmax+ 1 =imin。具体流程如图5 所示。 图5 优化计算流程图 考虑将无人机调整时的每一时刻分割都视为静止状态,从而独立考虑采用贪心算法进行实时定位且决定接下来的调整方案。 分析表1 的数据,发现编号为F1 的无人机在半径为100 m 的圆周上,所以假设编号为F1 的无人机位置无偏差。根据表1 的数据我们利用MATLAB 软件画出了无人机的初始点坐标,以F0为圆心,100 m 为半径的圆,以及每一架无人机均匀分布在圆上的最终结果,如图6 所示。从图6 可以得出,除了P0和P1外,其余所有的无人机位置都是有偏差的。 图6 无人机初始位置与目标位置图 针对无人机的调整方案,在某一时刻时,将除P0和P1外的所有待调整的无人机位置记为P。发射电磁信号的无人机位于点P0和P,接收信号的无人机位于点P1,可以得到α1,要将F3移动到目标位置P3,α1的角度应该为50°,其计算方法如下: 其中:P=P2(或P9)时对应的Pt为1,P=P3(或P8)时对应的Pt为2,以此类推,如图7 所示。 图7 点F3 和P0 发射电磁信号 记Δδ=|α1- ∠P0P1P3|为目前夹角与目标夹角的差值,Δδt为t时刻的Δδ,建立实时定位跟踪模型为 步骤一:将F3这个点分别向四周扩展一次(向四周移动一个小单位),移动一次后退回,观察α1的变化。如果α1的度数是趋近于目标位置的度数(50°),就向该方向继续移动,重复以上操作,直到α1= 50°。利用MATLAB 软件编程分析可得移动后的无人机F3是在射线P1P3上。 将F3通过上述步骤迭代到射线P1P3上后,发射电磁信号的无人机位于点P0和P1,F3作为接收信号的无人机,可以得到α2。要将F3移动到目标位置P3,α2的角度为50°,其计算方法与公式(11)一致,其中:P=P2时对应的Pt为1,P=P3时对应的Pt为2,以此类推,如图8 所示。 图8 点P0 和P1 发射电磁信号 步骤二:与步骤一类似,将F3这个点分别向四周扩展一次,移动一次后退回,观察α2的变化,如果角α2的度数是趋近于目标位置的度数(50°)时就向该方向继续移动,重复以上操作,直到α2= 50°。分析后可得出,移动后的无人机F3是在以O为圆心的圆上的。 重复步骤一和步骤二,分别以P0、P和P0、P1作为发射电磁信号的无人机,使用贪心算法[13]通过多次迭代之后可以将无人机的位置无限地接近目标位置,对于除P0和P1外的其他点也做以上步骤,最终可以得到均匀分布在一个圆上的9 架无人机。 贪心算法是指求解问题时,总是作出当前最好的选择,即不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解[14]。基于贪心算法思想,每次在调整无人机位置时都取得当时的局部最优解,找到与目标方向最接近的移动,最终得到完整的移动方案。 当α= 46.24°时,将∠PPjO从小到大依次标记为∠1~∠8,点P运动过程中∠PPjO实时变化情况如表2 所示。 表2 α=46.24°时点P 运动过程中∠PPjO 实时变化情况表单位:(°) 利用MATLAB 软件计算得到α= 46.24°时,Nmax= 2。当α= 37.96°时,将∠PPjO从小到大依次标记为∠1~∠8,点P运动过程中∠PPjO实时变化情况如表3 所示。 表3 α=37.96°时点P 运动过程中∠PPjO 实时变化情况表单位:(°) 利用MATLAB 软件计算得到:当α= 37.96°时,Nmax= 2,imin=Nmax+ 1 = 3。 经检验发现,当角度α改变时,不会使Nmax继续增大,那么只要再增加3 架发射信号的无人机就可以进行有效定位。定位精度不同,所需要的发射信号的无人机数量也不同。 本文采用纯方位无源定位的方法确定无人机的位置,利用实时定位跟踪模型和贪心算法思想,改变该实时定位跟踪模型相应的参数,实时追踪定位被动接收信号的无人机,调整位置略有偏差的无人机,使其适用于圆形编队队形。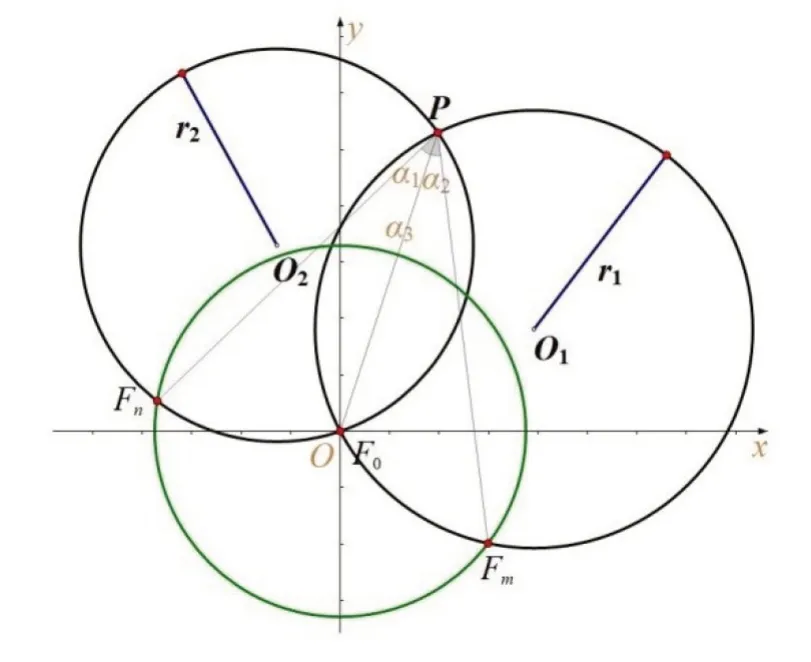


1.3 基于贪心算法思想建立实时定位跟踪模型
2 仿真研究


3 结语

