圆锥曲线中定点和定值问题的求解策略探究
李 波
(四川省南充高级中学,四川 南充 637901)
学习《圆锥曲线与方程》章节的内容,定点和定值问题是圆锥曲线的高频考点,该问题涉及圆锥曲线的定义、几何性质、直线与圆锥曲线的位置关系、极坐标系和参数方程等知识,与平面向量、函数与方程、不等式等代数知识紧密联系.
1 利用结论,快速秒杀



2 特值引路,先找后证

(1)求椭圆E的方程;
(2)直线MF1,NF1分别交椭圆E于C,D两点,设直线CD与x轴交于点P,证明:|PB|为定值.




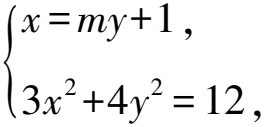
由根与系数的关系知
又F1(-1,0),所以直线MF1的方程为

由根与系数的关系知





直线PC的斜率为

当直线MN的斜率为0时,不满足M,N均在y轴的右侧.
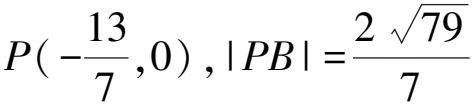
3 回归定义,以退为进


图1 例3示意图
(1) 求椭圆M的标准方程;
(2) 已知直线l与椭圆M相切于点P(x0,y0),且l与直线x=a和x=-a分别相交于C,D两点,记四边形ABCD的对角线AC,BD相交于点N.问:是否存在两个定点F1,F2,使得|NF1|+|NF2|为定值?若存在,求出F1,F2的坐标;若不存在,说明理由.

(2)当y0=0时,由图1知,显然不成立.
当y0≠0时,设直线CD的方程为
y=k(x-x0)+y0,

(1+4k2)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0.
由直线CD与椭圆相切知△=64k2(y0-kx0)2-4(1+4k2)[4(y0-kx0)2-4]=0.

即过点P的切线方程为x0x+4yy0-4=0.









4 几何特征,同一性转化

(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足,证明:存在定点Q,使得|DQ|为定值.


满足△=24+48k2-8m2>0,
由根与系数的关系知

当2k+2m=m+1时,m=-2k+1,直线MN的方程为y-1=k(x-2),即直线MN过点A,不成立;


5 观察结构,列式消元

(1)求C的方程;

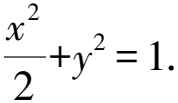
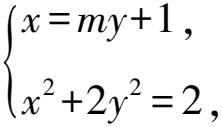
显然△>0,由根与系数的关系知





6 对偶运算,同构思想

(1)求曲线C的方程;


图2 例6解析图









7 参数方程,有效转化

(1)求椭圆C的方程;


(2)设E(m,0),m>0,直线l的参数方程为


(1+2sin2θ)t2+2mtcosθ+m2-6=0,
满足△=4m2cos2θ-4(1+2sin2θ)(m2-6)>0.
设|QA|=|t1|,|QB|=|t2|,
由根与系数的关系知

代入两根之和、积得


解析几何中的定点和定值问题是圆锥曲线的高频考点,突出了数学的学科特色,着重考查学生的理性思维和综合运用数学思想方法发现问题、分析问题、解决问题的能力,让学生思维的广度与深度得到充分的展示.

