利用导数求参数取值范围的若干策略
贺凤梅
(新疆伊犁巩留县高级中学,新疆 伊利 835400)
题目呈现(2022年山东数学模拟试题)已知函数f(x)=aex-1-lnx+lna,
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
1 总体分析
本题第(1)问考查导数的几何意义,属于常规题.第(2)问则是利用导数研究不等式恒成立问题,求参数的范围.此问可以多视角解答,涉及隐零点、同构法、切线放缩、分类讨论、反函数法等多种策略.
2 试题解答

以下重点探讨第(2)问.
视角1 隐零点.
解法1令g(x)=aex-1-lnx+lna-1,x∈(0,+∞),a>0,则

①
两边取自然对数,整理,得
lna+x0-1=-lnx0.
②

所以g′(x)在(0,+∞)上单调递增,
且x→0+时,g′(x)→-∞;
x→+∞时,g′(x)→+∞.
所以x∈(0,x0)时,g′(x)<0;x∈(x0,+∞)时,g′(x)>0.
因此g(x)在x=x0处取得极小值,也为最小值,即g(x)min=aex0-1-lnx0+lna-1.
显然,要使原不等式恒成立,必有
解得a≥1,即a∈[1,+∞).
评注此解法通过构造函数g(x),利用隐零点x0表示出g(x)的最小值,借助基本不等式得出关于a的不等式,求解即得[1].
视角2 同构.
条件f(x)≥1,即aex-1-lnx+lna-1≥0(*)在x∈(0,+∞)上恒成立.
解法2将(*)式变形得ex-1+lna+x-1+lna≥x+lnx=elnx+lnx.
构造函数g(t)=et+t,求导得g′(t)=et+1>0.
所以函数g(t)=et+t在R上单调递增.
由g(x-1+lna)≥g(lnx),得x-1+lna≥lnx.
即lna≥lnx-x+1在x∈(0,+∞)上恒成立.
令h(x)=lnx-x+1,x>0,

视角3同构+切线放缩.
解法3将(*)式变形,得
ex-1+lna+lnex-1+lna≥x+lnx.
构造函数g(x)=x+lnx,x>0,

由g(ex-1+lna)≥g(x),得ex-1+lna≥x.
结合ex≥x+1,得x-1+lna≥x-1.
所以lna≥0,解得a≥1,即a∈[1,+∞).
解法4将(*)式变形,得


构造函数H(x)=xex,x>0,H′(x)=(x+1)ex>0,
所以H(x)在x∈(0,+∞)上单调递增.
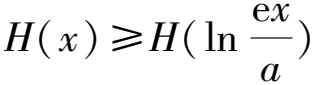
易证x≥1+lnx,所以lna≥0即可,解得a≥1,即a∈[1,+∞).
评注视角2中的三种解法均属于同构法,从解答过程可以知晓,根据不同的变形形式,得到有一定差异的同构函数,借助于函数的单调性,得出变量间的关系,进一步变形求解,问题也就迎刃而解了.当然,在解答的过程中,用到了ex≥x+1与x≥1+lnx这两个有关切线放缩的不等式,作为解答题,需要简单证明方可使用[2].
视角4 放缩+极值.
解法5由已知条件,得aex-1+lna≥1+lnx.
易证x-1≥lnx,即x≥1+lnx.
所以只需aex-1+lna≥x.
构造函数φ(x)=aex-1+lna-x,
求导得φ′(x)=aex-1-1.
以下对a分情况讨论:
(Ⅰ)当a≥e时,φ′(x)=aex-1-1≥e·ex-1-1=ex-1>0在(0,+∞)上恒成立,φ(x)=aex-1+lna-x≥e·ex-1+lne-x=ex-x+1>0(x>0),满足题意.
(Ⅱ)当0 所以φ(x)≥φ(1-lna)=ae-lna+2lna-1≥0. 所以lna≥0即可,解得1≤a 综上可得a∈[1,+∞). 评注此解法通过不等式放缩,介入中间量,借助于极值求解也可以成功突破.但因为定义域的限定,需对a进行分类讨论,再取两种情况的并集,此处易出现纰漏,值得大家重视.再给一例,感兴趣的读者可以自行求解或查阅. 已知函数f(x)=ex-2-lnx.若g(x)=f(x)+lnx-ax,讨论g(x)的单调性. 视角5 分类讨论. 解法6由f(x)=aex-1-lnx+lna,x∈(0,+∞),a>0,对a进行分类讨论: (Ⅰ)当0 (Ⅱ)当a=1时,f(x)=ex-1-lnx,则 x∈(0,1)时,f′(x)<0,f(x)单调递减; x∈(1,+∞)时,f′(x)>0,f(x)单调递增. 所以f(x)≥f(1)=1,满足题意. (Ⅲ)当a>1时, f(x)=aex-1-lnx+lna≥ex-1-lnx, 易证ex-1≥(x-1)+1=x, x≥1+lnx, 所以f(x)≥f(1)=1,满足题意. 综上可得a∈[1,+∞). 评注此解法属于对a进行分类讨论求解,通过推理和论证,符合就要,不符合则舍去.难点在于找参数a的分类界限,这需要通过日积月累的训练方能达成. 视角6 反函数. 解法7 由已知,得aex-1-lnx+lna≥1. 所以aex-1≥lnx-lna+1. 所以G(x)在(0,1)单调递增,在(1,+∞)单调递减. 则G(x)≤G(1)=1,故a≥1. 即a∈[1,+∞). 评注此法确实很巧妙,能通过变形、观察和求解得出不等式两边对应函数恰好互为反函数,利用凸凹反转,借助于临界的切线得出大小关系,化繁为简. 题1(2010年高考新课标卷理科)设函数f(x)=ex-1-x-ax2,a∈R.若当x≥0时,f(x)≥0恒成立,求a的取值范围. 题2若不等式ax-lnx≥a(2x-x2)对∀x∈[1,+∞)恒成立,求a的取值范围. 导数问题博大精深,对于学生而言,基础知识和基本理论易于学懂,但是,受众多关联知识和高数背景的限制,很多导数问题难以突破.对于高校来讲,导数是学生深造学习的重要基础.基于此种原因,高考一直重点考查导数,因此我们有必要多花时间和精力研究导数,总结规律,提炼解法,积累经验,创新思路,在比较和不断尝试中增长技能.这类参数问题入口宽,结果唯一,研究它就是对导数的全面理解和应用,这对我们的学习大有裨益.


3 试题链接

