非等谱的导数非线性薛定谔方程的双Wronskian解

林清芳,李 琪

(东华理工大学理学院,330013,南昌)

0 引言

非均匀介质中带导数的非线性薛定谔方程模型可由非等谱发展方程描述[1-2],该模型在离子体、非线性光学和空间凝聚态物理领域具有广泛的应用,正是在现实需求下,求解非等谱的导数非线性薛定谔方程十分有意义。文献[3]将反散射变换运用于非线性导数薛定谔方程。范恩贵由联系广义Kaup-Newell 谱问题导出DNLSI、DNLSII、DNLSIII方程,以及这些方程的统一式Kundu 方程[4],并通过达布变换导出一个非线性Schrödinger方程的孤子解[5]。翟雯[6]运用Hirota方法求得了广义带导数的非线性Schrödinger方程的精确解。宁同科[7]基于文献[8-9]的Wronskian技巧解得了非等谱sine-Gorden方程,非等谱非线性Schrödinger方程的双Wronskian解。Zhao等[10]求解了非等谱AKNS方程的孤子解并对该方程进行了非局域约化,进而得到约化后方程的孤子解。Li等[11]利用Hirota方法导出了一类具有导数的一般非线性薛定谔方程的多孤子解。本文是运用Wronskian技巧求解文献[12]导出的非等谱的导数非线性薛定谔方程,并将求解得到的双Wronskian解与文献[12]所求解的孤子解进行一致性检验。

本文将考虑一个广义非等谱的导数非线性薛定谔方程[12]如下:

(1)

其所对应的谱问题:

(2)

时间发展式为:

(3)

其中,q=q(t,x),r=r(t,x)位势函数,λ为谱参数,与x无关。

1 方程(1)的孤子解

作变量替换[1,6,11]

(4)

双线性导数形式可化为:

设f(t,x),g(t,x),s(t,x)与h(t,x)是关于参数ε的级数,

(5)

已知[12],取ε=1,则单孤子解为:

(6)

双孤子解为:

(7)

2 方程(1)的双Wronskian解

定理:双线性导数方程(5)有双Wronskian解:

(8)

其中,φj(x,t),ψj(x,t)满足条件:

φj,x=kj(t)φj,φj,t=2xφj,xx+αφj,x,ψj,x=-kj(t)ψj,ψj,t=-2xψj,xx-βψj,x,

(9)

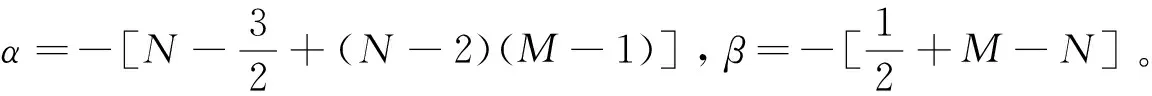
对φj,t,ψj,t进行对x求l(行数)阶偏导,则应有:

(10)

证明:1)计算双Wronskian行列式f,g,s,h对x的导数,得:

2)依据式(10)、(11)计算出双Wronskian行列式f,g,s,h对t的导数,得:

将f,g,s,h及对x,t的导数代回双线性形式5(a)中,并且有恒等式:

(11)

由行列式的性质:

①设aj(j=1,2,…,N)是N维列向量,γj≠0(j=1,2,…,N)是N个实常数,则

(12)

其中γaj(γ1a1,j,γ2a2,j,…,γNaN,j)T。

②设D为N×(N-2)矩阵,a,b与c都是N维列向量,则:

|D,a,b||D,c,d|-|D,a,c||D,b,d|+|D,a,d||D,b,c|=0.

(13)

根据恒等式(12),及行列式的性质(13)、(14)对式5(a)进行化简得:

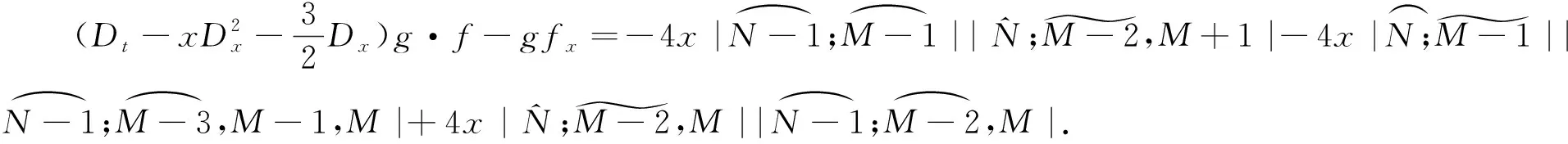
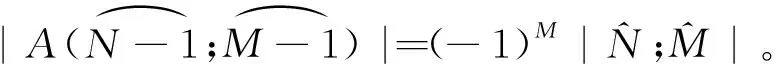
根据引理,因此式5(a)进一步有:

同理可得,双Wronskian 解(9)满足式5(b)。

类似地,将f,g,s,h及对x,t的导数代回双线性形式5(c),根据行列式性质(13)、(14)及恒等式:

(14)

式5(c)化简为:

又根据引理,式5(c)进一步得:

同理,双Wronskian 解(9)满足5(d)。

综上,双Wronskian行列式满足双线性导数形式,所以:

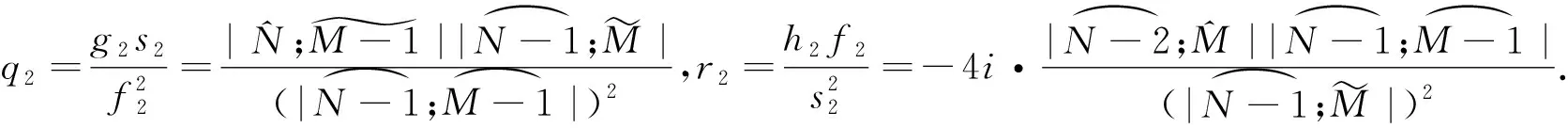
(15)

3 解的两种表示的一致性

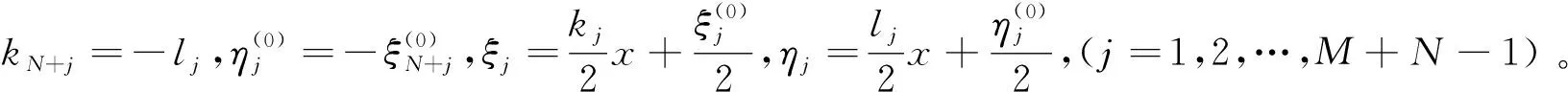
(16)

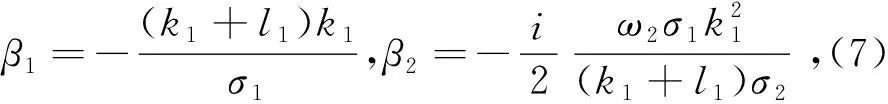
当N=2,M=2时,类似有k3=-l1,k4=-l2,此时计算f2,g2,s2,h2,并将其带入(4),取:

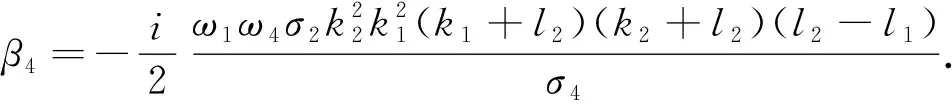
(17)

该解与(8)对比,两解形式一致。

故猜想当N=M时,Hirota形式的N-孤子解与双Wronskian解是一致的。

4 结束语

本文在运用Hirota方法求解非等谱的导数非线性薛定谔方程得到N-孤子解的基础上,采用Wronskian行列式技巧,进一步得到了该方程的双Wronskian解,并探讨了Hirota方法和Wronskian行列式表示解的一致性。在后续的研究工作中,将对该方程进行双Wronskian解约化,导出Matveev解、Complexiton 解、混合解等更多其他形式解,及研究方程的对称与无穷守恒律。