基于强混偏差样本的各向异性回归函数小波估计的相合性分析
陈 佳
(四川文理学院 数学学院,四川 达州 635000)
0 引言
设{(Xi,Yi),i=1,2,…,n}是定义在概率空间(Ω,F,P)上的同分布随机变量,其密度函数为:
(1)

x∈[0,1]d
(2)


1 各向异性小波理论和Besov空间


tτx=(tτ1x1,…,tτdxd);tτc=(tc)τ
定义指标集:

定义:
(3)
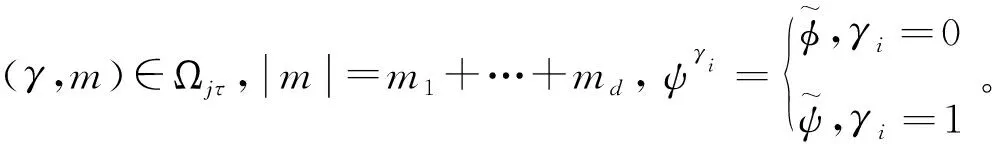

(4)
构成L2(Rd)的一组标准各向异性小波正交基,因此对任意的f∈L2(Rd)
(5)



(i)f∈Lp(Rd),




备注1:此定理蕴含着
(6)
假设回归函数r(x)属于H>0的Besov球,即
2 各向异性小波估计量
对模型给出一些假设,构造小波估计器,给出样本强混的定义。
定义2[12]:设{Xi,i∈Z}是严平稳的随机向量序列

对模型给出一些假设:
H1:存在常数c1>0,使得infh(x)≥c1,x∈[0,1]d
H2:ρ满足ρ∈L(Rd)∩L∞(Rd)。
H3:对任意(x,y)∈[0,1]d×R,存在常数0 H4:序列{(Xi,Yi),i=1,…,n}的强混系数满足α(k)≤λe-c4k,其中λ>0,c4>0。 H5:设f(X1,Y1,Xk+1,Yk+1)为(X1,Y1,Xk+1,Yk+1)(k≥1)的密度函数,f(X1,Y1)为(X1,Y1)的密度函数,存在常数c5>0,使得∀(x,y,x′,y′)∈[0,1]d×R×[0,1]d×R。 其中,hk(x,y,x′,y′)=f(X1,Y1,Xk+1,Yk+1)(x,y,x′,y′)-f(X1,Y1)(x,y)f(X1,Y1)(x′,y′)。 给出回归函数r(x)的小波估计量: (7) 其中: (8) (9) 由H1~H3可知定义是明确的,此估计量是r(x)的一个无偏估计,从引理2可得到证实。 =αjτ;k 另一方面: Φjτ;k(x)f(x,y)dxdy=αjτ;k 为证明主要结论,还需引用以下引理,其详细证明可参考文献[10]。 主要结果及相应证明如下: 证明:易知 (10) 只需估计式右侧的随机项和偏差项,先估计偏差项,利用Holder不等式和(θ)条: 根据式(6),当n→∞时,j→∞,则: (11) 根据Φjτ;k的紧支性和(θ)条件可得: 注意到|Λjτ|~2|jτ|,利用引理5可得: (12) 结合定理得证。 备注2:从定理的结论可以看到,当1≤p≤2空间为各向同性时(即s1=s2=…=sd=s),则s(d)=s与各向同性空间中的结果一致[7]。 小波独特的局部时频分析功能能够描述各向异性的Besov空间。小波方法被广泛应用于回归函数的估计问题,针对强混条件下带噪声各向异性回归估计模型,在各向异性Besov空间中构造了线性小波估计器,讨论估计器在Lp(1≤p<∞)风险意义下的相合性,为各向异性Besov空间研究回归函数的估计提供了理论指导。
3 主要结果
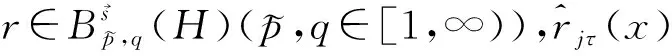

4 结束语

