改变奖金发放频率有助于增加雇员工作努力程度吗?——基于实验经济学的研究

王晓彦,雷雨田

〔1.苏州科技大学 商学院,江苏 苏州 215009; 2.中国人民大学 中法学院,江苏 苏州 215123〕

一、引言

效率工资理论是过去三十年里宏观经济学的主要发展分支之一,是现今劳动经济学的重要研究理论之一,其指出雇主支付雇员高于市场出清水平的工资能够有效地提升雇员的工作努力程度。效率工资的概念多年来早有实践,索洛模型是效率工资理论里最具有代表性的模型。但在索洛模型中,影响雇员努力工作的仅仅是工资水平,存在较大的缺陷。现今的学术界基于索洛模型进行了深入和细化。在国外,比较有代表性的有考虑相对工资水平的萨摩斯模型、考虑失业率的罗默模型以及偷懒模型、工作转换模型等等。国内也有肖永基于代理理论和强制性储蓄理论的研究,邸晓燕和孟颖基于“交保证金”对有关模型的拓展。在这些对效率工资理论进行拓展的研究中,起源于行为经济学的实验劳动经济学为相关研究提供新的视角。

基于纯粹理论推导的模型存在与现实经济运行不符的问题。劳动实验经济学从心理学、博弈论等行为科学出发,所获得数据皆来自与现实接轨的实验,所得出的结论也具有现实意义。自阿克罗夫第一次依托礼物交换博弈进行劳动实验经济学研究后,劳动实验经济学已经有了许多重要的成果。

在现有的工资框架下讨论时间偏好存在着一定困难,因为在目前的劳动市场里按月结算工资是主要的工资发放形式。为了使研究成果更加具有现实借鉴意义,本文将从另一个重要的劳动效率激励机制——奖金维度出发进行时间贴现偏好讨论。在现实的劳动雇佣关系中,除了基础工资以外,“奖金”“津贴”“福利”也是重要的员工激励手段。为了使雇员的工作更有效率,寻找合适的方法来发放奖金就具有一定的研究意义和现实意义,从时间贴现偏好的视角出发,这个命题可以转变成“如何通过改变奖金发放的时间来增加员工的效率”。

基于以上认知和学术界已有的研究,本文利用劳动实验经济学的方法重点探讨时间贴现偏好与雇员效率之间的关系。本文首先从索洛模型出发,对索洛模型中的工资水平重新定义为效用感知工资水平。然后为了讨论时间贴现偏好对效率工资的作用,本文在模型中引入了奖金和工资发放周期的概念,用于表示一整个工作时间段中发放外生激励——奖金的次数。

本文的研究创新主要聚焦于以下几点。一是完善了效率工资理论模型:本文主要从效用论视角出发,通过引入奖金和时间贴现偏好构建了一个效用工资感知水平方程,该方程较之于传统的只考虑绝对工资水平的索洛模型,对劳动雇佣关系中员工效率的表现具有更好的经济学解释力。同时该模型可以引入更多的效率影响因素如公平、工作环境,为后续的相关研究提供了理论基础。二是研究既具有理论价值又具有现实价值:本文利用实验经济学工具检验了时间偏好在各种雇佣条件下的表现,极大丰富了该概率的内涵,对该理论的发展做出一定贡献。同时,本文的研究成果为现实雇佣关系中的领导者提供了一种奖金激励模式,领导者可以基于本文的研究成果设计出合理的奖金发放制度,促进员工工作效率提升。最后提供了一个自然实地实验的实践模板:自然实地实验的数据较之传统的实验室方法更有现实说服力,但是由于实施难度较大,相关实践一直较为缺失。本文提供了一个可以在大学环境中实施的自然实地实验的方法,为该研究方法的实践拓宽了思路。

二、模型构建与实验假设

1.基于索罗模型的奖金时间贴现偏好模型构建

结合过往实验经济学对效率工资理论的补充,在传统的效率经济模型——索洛模型的基础进行一定的补充和重新定义。

索洛模型中关于工资与雇员努力程度的表达式如下,式中e代表了雇佣工作效率,假设该式单调递增:

e=e(w),e′(w)>0

(1)

该式中w仅为一般的绝对工资水平,忽略其他许多要素对雇员努力程度的影响。因此,结合过往的研究成果,从效用论角度出发,对该模型进行细化:

e=e(Wu),e′(Wu)>0

(2)

Wu=U(W,T,F,C,A…)

(3)

在这个新的模型中,将索罗模型中的绝对工资水平重新定义一个新的变量:Wu效用感知工资水平,其用于表示雇员在该工资水平下,所感知获得的效用,该效用越高,雇员的努力程度越大。Wu的形成受多种因素影响,如基于索洛模型的W绝对工资水平,E为奖金水平,基于时间贴现偏好的T奖金发放周期,基于社会学模型的F公平程度,基于偷懒模型的C雇员在工作中所耗费的精力,以及基于萨摩斯模型的A工资相对预期。本文的讨论重点主要是奖金里时间贴现偏好对雇员努力程度的影响,因此在进一步的模型构建中,将模型简化如下:

Wu=U(W,E,T)

(4)

设奖金E与工资发放周期T存在以下关系:

E=TEt

(5)

Et为每个周期所获得的工资,方程可以变换成:

Wu=U(W,TEt,T)

(6)

引入时间贴现偏好指数UT,其值与时间周期T相关,表示雇员存在着时间贴现偏好对方程进行如下定义:

Wu=U(W,TEt,T)=W+UTTEt

(7)

该方程的含义是:在其他因素被控制的情况下,效用工资感知水平为在劳动总时间里带有时间贴现偏好的奖金与绝对工资数量的综合作用所产生的值。时间贴现偏好系数的存在使得当UT≠1时,效用工资感知水平≠绝对奖金水平+绝对工资水平。值得注意的是,该式中隐含在一整段时间里雇员在所有的时间周期保持着一样的时间偏好,为了使方程更加一般化,设方程为:

(8)

在这个方程中Eu表示奖金带来的效用,为每个时间周期的时间偏好。Ut与t为每个周期所获得的Et的综合作用。当对任意的Ut存在着UT=TUt方程(7)与方程(8)相等,仿照方程(2),定义一个方程:

Eut=UtEt(t=1.2.3…T)

et=f(Wut)=f(Wt+UtEt)

(9)

方程(9)用于反映某一个时间周期的雇员努力程度。

现将整个公式和相关变量解释整理如下

e=e(Wu),e′(Wu)>0

(2)

Wu=U(W,T,F,C,A…)

(3)

Wu=U(W,E,T)

(4)

E=TEt

(5)

Wu=U(W,TEt,T)

(6)

Wu=U(W,TEt,T)=W+UTTEt

(7)

(8)

Eut=UtEt(t=1.2.3…T)

et=f(Wut)=f(Wt+UtEt)

(9)

2.对时间贴现偏好的进一步探究

假设时间贴现偏好的存在具有合理性,那么它是如何激励雇员努力程度的?这个逻辑路径值得探讨。我们注意到,传统的e=e(w)忽略了对时间维度的思考。如果单纯从e=e(w)的式子出发,雇员应该只在获得酬劳的那一刻有激励来工作,获得酬劳前和获得酬劳后工资带来的激励消失。这与现实状况大相径庭。因此,我们可以合理地假设,酬劳对雇员的激励不是时刻性的,而是时段性的。雇员在获得酬劳前存在着努力工作的激励,获得酬劳后也存在努力工作的激励。

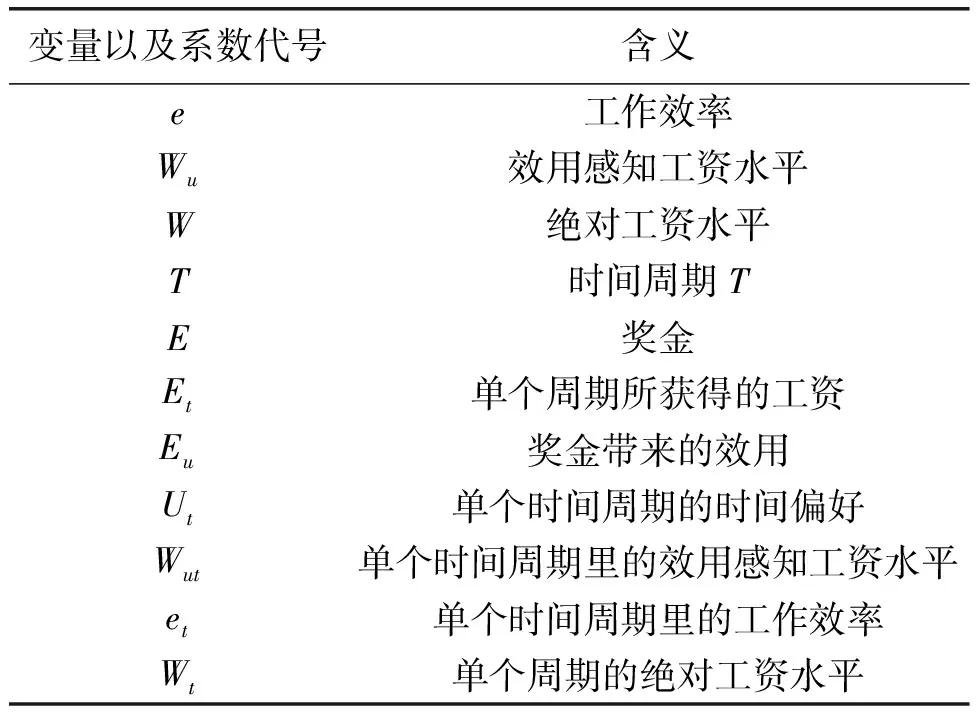
表1 变量及系数解释表

因此,合理地假设时间贴现效应符合一个简单的单峰线,也就是说酬劳带来的激励在不同时间段不均衡,而是随着时间离酬劳发放的时间点越远激励越低。

最后,为了后续讨论方便也使得模型更加具有现实意义, 将时间贴现偏好中的时间内涵进行拓展,一种是常规意义上的工作时间,另一种则是将一个雇员的总任务量作为其“工作时间”综合,也就是人们完成一单位工作取决于其工作的性质,该单位可能是时间尺度也有可能是任务量尺度,都有实现贴现的激励。

3.实验假设

基于上述理论模型,提出以下几个实验假设。

H1:时间贴现偏好存在,且对雇员努力程度有着正向的促进关系。

我们认为由于时间贴现偏好的存在,当雇员的时间偏好被满足时,所感受到的Wu增加,从而加大自己的努力程度。

H2:雇员努力程度随着T的增加而增加。

时间贴现偏好理论认为人们会倾向于将自己的每一个片段都实现效用最大化,基于此本文假设当雇员被激励得越频繁,展现出更大的时间贴现偏好,从而增加雇员努力程度。

H3:时间贴现偏好在不同的时间周期下会有不同的表现。

理论模型中假设时间贴现偏好系数是随着时间周期T变化而变化,不同的T可能会造成时间贴现偏好的不同。

H4:雇员存在着奖金发放激励。

H5:雇员存在着奖金后激励。

H6:奖金的激励会随着时间距离的增加而减少。

基于上述论证,我们认为雇员在获得奖金的前后时间段存在激励,且这种激励会随着时间距离的增加而减少。

三、实验设计与实验过程

1.实验设计

为了较为全面验证实验假设,本文设计了两大类共四种实验环境,详情见表2。

如表2所示,第一类的实验环境模拟的是现实生活中计件制的奖金制度,在实验中以整场实验者所需要完成的任务量作为周期,也就是模拟模型中T以总体劳动量为内涵的情况。我们将实验者分为四组,分别是完成后给予奖金(base组),每完成一半后给予一半奖金(T/2组),每完成三分之一后给予三分之一奖金(T/3组),每完成六分之一后给予六分之一奖金(T/6组)。由于所有实验者最终完成的任务量是相同的,于是判断效率高低的标准是完成的时间,第一大类中两种子实验在条件上的区别在于实验者是否知道任务量的具体数目,这与现实生活中计件制的情况相符合。但其实第一子类和第二子类所需完成的数量是一样的,以达到控制实验变量的目的。

第二类的实验环境模拟的是现实生活中计时制的奖金制度,在实验中以整场被试者所需要完成任务的时间作为周期,也就是模拟模型中T以劳动时间为内涵的情况。同样,我们将实验者分别记为四组,分别是完成后给予奖金(base组),每完成一半后给予一半奖金(T/2组),每完成三分之一后给予三分之一奖金(T/3组),每完成六分之一后给予六分之一奖金(T/6组)。由于所有被试者最终完成后所需的时间是相同的,因此判断效率高低的标准会是一个由第三方对被试者的工作评分,第二大类中两种子实验在条件上的区别在于实验者进行任务的工作周期时间长度。第一子类为3小时,第二子类为一学期,用于检验在短时间周期和长时间周期中理论的合理性。

2.实验过程

2022年9月至2023年1月,本实验在湖南省H大学开展。为了获取实验数据以及保证实验数据的规范性以及对现实经济生活的反映。本文采取实验室实验与自然实地实验方法相结合的实验过程。第一大类的实验背景如下,H大学有一大批图书资料需要录入电子系统,该校将此项任务向学生公开,按照该校学生工作规定给予劳务奖励,该实验背景与现实经济生活中的情况相类似。该活动一共招募了3期,每次招满40人,且报名参加过的学生无法再次报名,保证了学生作为被试者不会重复参与实验。分组时将学生报名表进行随机生成再排列,以达到随机组合的效果。实际实验中,我们将四组被试者分配到四个不同的机房,并在实验开始前告知其奖金发放模式,并对电子图书的录入进行培训并让其进行演练。对于第一子类实验的被试者告知任务总量60本图书,对于第二子类则不告知。所有被试者在同一时间开始工作,实验过程中没有出现被试中途离开或者任务未完成的情况,所有图书的录入为一套统一的标准。对于效率的检测则是在机房的电脑后台运行了一套计时程序,每当被试者完成十件也就是T/6的时候记一次时。

第二大类的实验背景更接近于自然实地实验,该实验展开依托于H大学的学生会组织,所有成员均是学生会成员,学生会中对各成员或者各部门分配的长短期任务以及其给予的劳务可以近似模拟现实经济生活中的工作情况。第一子类实验围绕学生会的一个咨询计划展开,一共招募了40名被试者,并均分为四组。该咨询一共持续时间为3个小时,学生会相关领导按照其内部绩效评分规则每半小时对被试者的表现进行评分,该评分过程实验者全程无干扰,学生会相关评分领导也不知道实验目的。类似的,第二子类实验则是依托学生会一个以学期为单位(3个月)的长期工作,追踪观察学期初进行了随机人员分配且人员数目相等的十二个小组,并被均分为四组的人员情况。由学生会相关领导每半个月对每组进行一次评分。两种子实验都不会在中途告知被试者(组)他们的绩效。

四、实验结果分析及假设验证

1.实验结果

(1)第一大类实验结果

图1、2分别展示了第一大类实验中两种实验环境的实验结果,纵坐标Time反映了被试者每完成十本图书也就是以任务量为周期的T/6所耗费的时间,时间消耗得越少,则认为被试者的效率越高。根据图1、2以及发放劳务的时间点对四组的实验结果进行分析:

图1 实验局1实验结果

首先对实验局1的各组结果进行横纵向对比分析。在Base组中,发现被试者的效率在逐渐下降。这是因为随着工作的增加被试者逐渐感到疲惫,但横向比较发现,在奖金发放(t6)的前一期(t5-t6)效率出现了增加。在T/2组中,首先与Base组进行纵向对比,整体上效率有着一定提升。在奖金发放(t3)的前后两期(t2-t3, t3-t4),效率都有着明显提升,t4-t5效率仍然高于Base组,但是效率有所下滑。横向比较发现奖金发放的前后两期呈现出效率上升趋势。然后观察T/3组,与Base组、T/2组进行纵向对比发现整体效率有着明显提升。横向比较来看,在前两次奖金发放t2的前后两期,t4的前一期效率都呈现上升态势,不过后续效率出现一定降低,且没有出现前两组出现过的在奖金发放(t6)前一期(t5-t6)的效率增加。最后T/6组效率优于Base组和T/2组,但是不如T/3组。横纵向比较发现,前四期效率较高,但在后两期出现了明显上升,这与Base组的整体趋势相同,且同样没有出现前两组出现过的在奖金发放(t6)的前一期(t5-t6)的效率增加。

图2 实验局2实验结果

对实验局2的局内数据进行分析,同时与实验局1的数据进行比较。在实验局2中,四组的整体趋势看来与实验局1相似,由于对实验外部条件进行了控制,出现该结果是正常的,同时进一步说明实验数据结果的稳定性。但是值得注意的是,Base组在最后一期(t5-t6)没有出现效率增加的情况。

(2)第二大类实验结果

图3、4分别反映了第二大类中两种实验环境的实验结果,纵坐标Score在实验局3反映被试者每半个小时所得到的绩效评分,在实验局4反映被试者以一学期为周期的T/6所得到的绩效评分。当评分越高时我们认为被试者的效率越高,根据图3、4以及发放劳务的时间点,对四组的实验结果进行分析:

在实验局3中,可以发现Base组中整体来说效率情况较为稳定,没有出现十分明显效率波动,但在奖金发放(t6)的前一期(t5-t6)效率出现了明显增加。在T/2组中,同样与Base组进行纵向对比,整体上效率有着一定提升。发现在奖金发放(t3)的前后两期(t2-t3, t3-t4)效率都有着明显提升,(t4-t5)效率仍然高于Base组但是效率有所下滑,与Base组相似。横向比较发现奖金发放的前后两期呈现出上升趋势。类似在T/3组中,与Base组、T/2组进行纵向对比,发现整体上效率有着明显提升,横向比较来看,前期有着较为明显上升,后期平稳地保持较高水平效率,但没有出现前两组出现过的在奖金发放(t6)的前一期(t5-t6)的效率增加。最后观察T/6组,整体上效率优于Base组,但是不如T/2组、T/3组。横纵向比较发现,其整体趋势与Base组较为相似,但水平更高。

图3 实验局3实验结果

图4 实验局4实验结果

以同样的视角来分析实验局4的数据。在Base组中整体保持平稳,没有出现较大波动,且与短时间周期实验情况不同的是,奖金发放(t6)的前一期(t5-t6)效率并没有出现明显增加。在T/2组中,与Base组进行纵向对比,整体上效率有一定提升。效率水平只有一次较明显的提升,同样未出现效率明显增加。同样在T/3组,与Base组、T/2组进行纵向对比,发现整体上效率有着明显提升。效率整体呈现“M”形状,更明显地反映了效率的提升在工作发放之后。最后在T/6组中,整体上效率优于Base组、T/2组,但是不如T/3组。整体上趋势与Base组较为相似,但水平更高。

2.假设检验

H1:时间贴现偏好存在,且对雇员努力程度有着正向的促进关系。

根据实验结果,我们可以发现该假设成立,在四种实验环境下,对奖金进行了周期发放的组(T/2, T/3, T/6)被试者努力程度都比base组要高,说明了时间贴现偏好存在,且对雇员努力程度有着正向促进关系。为了进一步验证假设,以个人努力程度为被解释变量,如果数据来自base组,则哑变量为0,其余为1。(1)由于实验局1、2中时间越短效率越高,在回归时进行了正向化处理——用20减去所耗时间。回归结果如表3所示。

可以看到,在四种实验环境下,哑变量系数都明显大于零且显著,严谨地证明了时间贴现偏好存在,且对雇员努力程度有着正向促进关系。

H2:雇员努力程度随着T的增加而增加。

通过对实验数据的观察,我们可以发现这一假设有一定的准确性,在4种实验环境下均发现被试者努力程度整体上存在着T/3组>T/2组>base组的情况,但是没有出现T/6组的被试者努力程度大于T/3组的情况。为了进行统计学验证,对数据进行两两分组依次进行回归分析,回归结果如表4所示。

如之前所分析,在四种实验环境中T/2组相对 base组、 T/3组相对于 T/2组的哑变量系数都明显大于零且显著,部分说明了雇员努力程度随着T的增加而增加,但是T/6组相对于T/3组却是负数,没有说明雇员努力程度随着T的增加而增加,说明该假设存在着一定局限。

H3:时间贴现偏好在不同的时间周期下会有不同的表现。

该假设可以从两个角度来验证,第一个是雇员努力程度的量方面,由于H1得证,可以说明不同时间周期下被试者努力程度在量上不同;第二个是被试者努力程度的变化趋势,由图1—图4可以明显发现,各组被试者努力程度变化趋势存在着明显不同,利用统计学工具进一步进行检验,对每一组实验数据进行轮廓检验, 结果如表5。

可以发现,拒绝接受这四条线互相平行,H5在两个角度得证。但进一步细化研究发现,在各实验环境中,T/6组趋势与base组十分相似,尤其是在实验进程过半后。因此分别对各实验环境中的base组与T/6组以及t3之后的base组与T/6组进行轮廓检验,结果如表6。

表3 实验局1—4回归检验表

表4 分组检验表

表5 轮廓检验图

表6 平行检验表

可以发现base组确实与T/6组存在着轮廓平行,但轮廓并不重合,H5并未被推翻,该现象发生原因仍值得进一步讨论。

H4:雇员存在着奖金前激励。

H5:雇员存在着奖金后激励。

H6:奖金带来的激励会随着时间距离的增加而减少。

对于H4,一个有力证据是在纵向对比视角下第一大类实验局1中,Base组在最后一期(t5-t6)出现了效率增加的情况,而实验局2中,Base组在最后一期(t5-t6)没有出现效率增加的情况。回顾实验条件,实验局1中的被试者知道在最后一期完成后可以获取奖金,而实验局2的被试者则不知道,实验局1的被试者相对于实验局2存在着一个奖金前激励。横向对比情况下,实验局1-3也在出现了大量在发奖金前效率的提升或者维持在一个高水平的情况下。

对于H6,观察各组的被试者努力程度图(图1-4)中的T/2、T/3可以发现,在发放奖金的时间节点前后,被试者努力程度往往呈现倒“V”形,这与在理论假设中提出的模型形状较吻合。

由此,基本上认为H4、H5、H6成立。

五、 结论与展望

1.研究结论

根据前文研究,得出以下结论:

第一,通过将奖金按照时间周期发放能够有效利用雇员的时间贴现偏好,并实现雇员努力程度的提高。本文通过实验发现,对于劳动雇佣者来说,将奖金均分为几个周期发放能够在奖金总成本不变的情况下有效提供雇员的努力程度,从而实现产出的更大化。该发现为劳动雇佣者提供了一个不增加成本提升雇员效率的方法。

第二,劳动雇佣者应该选择最合理的奖金发放周期以实现雇员努力程度提高的最大化。将奖金按照时间周期发放确实能够有效利用雇员的时间贴现偏好,但不同周期所带来的效果不同,雇员努力程度并不完全随着周期的增加而增加。在本文实验中,以T/3的时间节点发放奖金是效率最高的奖金发放方式,而不是奖金发放更加频繁的T/6组,这或许可以得出来适中的奖金发放间隔能够更好激发出雇员的时间偏好。

第三,劳动雇佣者应该根据自己所从事的劳动不同选择不同的奖金发放模式。本文一共模拟了四种实验环境,并发现每种生产模式下同样的奖金周期所激励出的雇员努力程度存在着一定差距。另外时间贴现偏好在不同的时间周期下也会有不同的表现。

第四,由于奖金在发放前和发放后都对雇员存在激励,且这种激励会随着时间距离的增加而减少。劳动雇佣者可以基于这种认知设计出合理的效率激励机制。

2.研究不足与展望

本文仍存在进一步深化研究的空间。第一,本文尚未令人信服地说明为何T/6组表现不符合理论模型,即激励的效果相对来说不明显。有一种可能性是由于奖金发放频率增加导致的单次奖金减少从而使得激励效果十分微弱。另一种猜想则是依据T/6组与base组的趋势相似,时间贴现偏好的实现有一个隐性前提是雇员对奖金发放周期的预期,我们在实验前期调研了解到很多被试者一开始以为是完成任务后才拿到劳务,过于频繁的奖金发放可能改变被试者对奖金发放周期的预期,使得贴现激励效果被减弱。第二,仍可以在实验中增加实验时间长度。本文只讨论了一个时间段里的奖金周期效果,但现实经济中劳动雇佣关系是长期的。因此在后续的研究中可以将研究进一步深化,探讨时间贴现偏好的产生条件、持续条件和对雇佣效率的作用路径。