构建函数模型 巧解最值问题
文/郭永胜
在解决某些最值问题时,我们可以通过构造二次函数模型,依据二次函数性质进行求解。现将这类最值问题归纳整理如下,希望对同学们解决此类问题有所帮助。
一、求代数式的最值
例1 已知实数m、n满足n-m=1,则代数式m2+2n-6m+7的最小值是______。
【分析】n-m=1 变形可得n=m+1,替换所求代数式中的n,得到关于m的二次多项式。
解:令y=m2+2n-6m+7。
∵n-m=1,∴n=m+1。
∴y=m2+2n-6m+7=m2+2(m+1)-6m+7=m2+2m+2-6m+7=m2-4m+4+5=(m-2)2+5。
∵此抛物线开口向上,∴当m=2时,y取最小值,最小值为5。
变式 已知实数a、b满足a-b2=4,则代数式a2-3b2+a-14的最小值是____。
【分析】a-b2=4 变形得到b2=a-4,替换所求代数式中的b2,得到关于a的二次多项式。但要注意b2=a-4≥0。
解:令y=a2-3b2+a-14。
∵a-b2=4,∴b2=a-4。
∴y=a2-3(a-4)+a-14=a2-3a+12+a-14=a2-2a+1-3=(a-1)2-3。
此抛物线开口向上,对称轴是直线a=1。又b2=a-4≥0,即a≥4,∴当a≥4 时,y随着a的增大而增大。∴当a=4 时,y取最小值为6。
【反思】以上问题属于由已知等式求未知代数式的最值。每个题目中含有两个字母,类比解方程组的“代入消元法”将所求代数式变为只含有一个字母的二次多项式。同学们要注意,我们必须先明确字母的取值范围,再结合二次函数性质准确求值。
二、求几何图形的最值
例2 如图1,正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN,则CN的最大值是________。
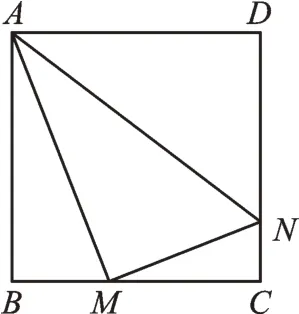
图1
【分析】由图可知,点N随着点M的运动而运动,CN的长度随之改变。设BM=x,用含x的代数式表示CN,将CN看作关于x的二次函数。
解:设BM=x,则MC=4-x。
根据“一线三等角”易证△ABM∽△MCN。

∴当x=2 时,CN取最大值,最大值为1。
变式 如图2,D、E、F分别是△ABC三边上的点,其中BC=8,BC边上的高为6,且DE//BC,则△DEF面积的最大值是________。
【分析】由图可知,求△DEF的面积就是求边DE的长度及DE边上的高。边DE的高随DE长度的变化而变化,设DE=a,用含a的代数式表示DE上的高,则△DEF的面积可看作关于a的二次函数。

图2

图3
解:如图3,过点A作AM⊥BC,垂足为M,交DE于点N,则AN⊥DE。
设DE=a。

∴当a=4时,S有最大值6。
【反思】以上问题属于几何图形中常见的求线段、面积最值的题目。解题时常利用全等三角形的对应边相等、相似三角形的对应边成比例、勾股定理、面积公式、三角函数等知识建立各个量之间的关系,再设未知数进行“量化”,得到相应的二次函数。

