含减纱2.5D 机织碳/环氧复合材料低速冲击损伤机制
张典堂,窦宏通,董 放,江 昊
(江南大学生态纺织教育部重点实验室,江苏 无锡 214122)
近年来,随着2.5D 机织预成型技术的日益成熟及机械自动化程度的提高,2.5D 机织复合材料因其细观结构设计性强、力学性能优异和近净成形等优势,愈发广泛地应用于航天发动机喷管、航天天线罩和航空发动机燃烧室火焰筒等锥形回转体部件[1]。然而受限于锥形回转体复杂成形工艺,其理论研究远落后于应用。因此,开展锥形回转体用2.5D 机织复合材料结构设计和力学性能分析,进而提升材料-结构性能匹配,是目前工程和学术领域的前沿工作。
加减纱工艺是2.5D 机织锥形回转体成形的核心技术,即随着锥形圆周周长的不断变化,为保证全场纤维体积含量或厚度一致,纱线数量随之要增加和减少。然而,加减纱会造成局部细观胞元的变化,方法不当易形成孔洞缺陷[2]。重要的是,2.5D 机织锥形回转体复合材料制备和服役过程中,不可避免地会遭受工具掉落和外物碰撞低速冲击载荷,而这将可能导致加减纱处形成损伤“弱结”,而进一步的面内压缩将导致结构失稳或失效。围绕加减纱2.5D 机织复合材料,研究人员开展了一定的工作,刘俊岭[3]围绕减纱结构对三维机织复合材料的影响,分别制备了经纱、纬纱、衬经纱、衬纬纱不同组合的含减纱结构异型件和正常结构件。通过试验研究了其拉伸力学性能,结果表明,含减纱结构异型件的拉伸强度和模量保留率在90%左右,证明了采用加减纱工艺生产的三维机织复合材料性能可以被较好的接受。陆慧中等[4]针对2.5D 机织结构,提出了5 种不同引纱加纱的方法,实现在织物特定位置加入纱线,增加复合材料纤维体积分数的目的。金星瑜[5]针对碳纤维2.5D 机织复合材料导弹发射箱盖的应用,设计了预置抽纱缺陷的2.5D 机织复合材料,通过试验和有限元的方法来探究其拉伸性能,并通过结构仿真的方法较好地验证了箱盖薄弱区域减纱结构形式的合理性。目前针对含加减纱结构2.5D 机织复合材料的研究大多集中在静力学行为研究方面,针对加减纱2.5D 机织复合材料在动态冲击载荷下的研究还鲜有报道。
近年来,随着CAE 软件的快速发展,国内外学者采用先进的数值模拟技术,开展了非常多的对2.5D 机织复合材料的力学性能的研究。在数值模拟方面,目前被广泛应用的有限元模型有细观单胞模型、全尺寸细观模型、多尺度混合模型和宏观均质模型等。例如:Wintiba 等[6]建立了一种考虑纱线接触条件2.5D 机织复合材料的细观单胞RVE 模型,通过RVE 模型计算验证,表明了该离散化RVE 模型可用于基于计算均质化的参数化研究。Cao 等[7]围绕着2.5D 机织结构,提出了不同纬纱截面2.5D 机织复合材料的全尺寸细观模型,开展了其在不同的冲击载荷下的损伤效果的探究,证明了全尺寸细观模型可以良好地反映出材料内部细观损伤形式。Durville 等[8]采用了一种隐式方法,在考虑纱线相互挤压的境况下建立了5 层2.5D 机织复合材料细观有限元模型。研究表明,该模型可以良好预测材料的压缩力学性能,并展现出了复合材料在多种负载下的非线性行为。Patel 等[9]围绕着2.5D 机织厚对称织物,建立了考虑细观纱性能多尺度混合模型,开展了其在轴向拉伸作用下力学性能研究。结果证明该多尺度混合模型可以准确地表达材料内部渐进损伤形式和整体材料件的强度和刚度。宏观均质模型计算效率较高,但是预测准确性难以保证。全尺寸细观模型准确性较高,但是对计算机的配置要求非常高。因此,如何既能保证复合材料数值计算准确性,又能提升计算效率仍是当前2.5D 机织复合材料冲击性能数值模拟技术面临的难点问题。
本文针对锥形回转体近净形常用的加减纱工艺,选用碳纤维和环氧树脂制备了不含减纱、含半列减纱和含整列减纱的2.5D 机织复合材料。设置54 J 和72 J冲击能量,采用落锤冲击仪,对3 种试样开展了低速冲击试验。得到了3 种试样的载荷-时间曲线,并利用Micro-CT 技术开展了损伤形貌和损伤量化分析。基于冲击损伤的“局部”分布特征,建立了宏-细观混合有限元模型。通过试验与模拟结合的方法,揭示含不同减纱结构的2.5D 复合材料低速冲击力学行为和损伤分布,有效地平衡了计算精度和计算效率,为异型构件的数值模拟提供了参考。
1 试验材料及方法
1.1 试验材料
本实验选取T700-12K 碳纤维,分别设计和制备了不含减纱、含半列减纱和含整列减纱等3 种预制体,其减纱方式和预制体形貌如图1 所示。

图1 不含减纱、含半列减纱和含整列减纱方法及预制体Fig.1 Methods and prefabricated bodies without yarn reduction,with half rows of yarn reduction and with all rows of yarn reduction
图1 中,织造半列减纱预制体时先减半列经纱,织造三纬以后再减去剩余的半列经纱,共进行2 次减纱操作,整列减纱预制体织造时只进行一次减纱操作。
在此基础上,选用E-51 双酚A 型环氧树脂,采用树脂传递模塑(RTM)工艺制备了不减纱2.5D 机织复合材料(NO-YR)、含半列减纱2.5D 机织复合材料(HIN-YR)和含整列减纱2.5D 机织复合材料(AINYR)。各复合材料基本参数如表1 所示。

表1 制备完成复合材料参数Tab.1 Parameters of prepared composite material
1.2 低速冲击试验
根据ASTM D7136/D7136M-15 标准,将制备好的复合材料通过精雕机切割成长150 mm×宽100 mm 的标准试样[10]。为了保证冲头在冲击过程中能够落在缺陷区域,在切割过程中,减纱区域被准确地控制在试样的中心。
采用Instron Dynatup 9250HV 落锤冲击仪,分别设置54 J 和72 J 总冲击能量对每种试样进行低速冲击试验,每组试验重复3 次,试验结果取其平均值。冲头为质量5.607 kg、直径16 mm 的半球形冲头。
1.3 Micro-CT 测试
采用Diondo d2 型微计算机断层扫描仪对冲击前后的3 种试样进行Micro-CT 图像采集和分析。采用的加速电压为90 kV,电流为90 μA。样品以相同增量旋转360°,采用的曝光时间为2 000 ms,共拍摄获得1 785 张投影。这些投影是通过像素大小139 μm、像素为3 072×3 072 的平板探测器收集的。扫描区域体积为30 mm×30 mm×3.6 mm,扫描精度为12 μm。
2 2.5D 机织复合材料宏-细观混合有限元模型
2.1 单胞性能预测
基于Micro-CT 提取的纱线截面图像,将纬纱和接结经纱的截面形状分别视为六边形和矩形,根据复合材料的组分属性、实际厚度和经纬密等参数,计算建立细观模型所需要的参数,并于建模软件中建立了细观单胞模型,如图2 所示。建立的单胞模型由基体和纤维束2 种组分的材料组成。在实际中,纤维束内部会浸润基体,形成浸胶纤维束。因此,基于混合定律[11]计算出浸胶纤维束的工程常数。计算结果如表2 所示。

表2 浸胶纤维束的工程常数Tab.2 Engineering constants of impregnated fiber bundles
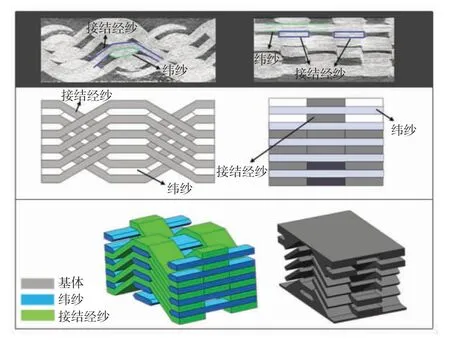
图2 细观单胞模型Fig.2 Meso-scale cell model
表2 中:E代表拉伸模量;G代表剪切模量;μ 代表泊松比。下标中的1 代表浸胶纤束轴向;2、3 分别代表与浸胶纤维束轴向相互垂直的切向;x、y、z代表截面的方向。
施加周期性边界可以保证单胞应力传递的连续性。本文中的单胞周期性条件如公式(1)—公式(4)所示[12]。
式中:u为位移;为单胞平均应变;xk为单胞内的任意一点坐标;j+为沿xk轴的正方向;j-为沿xk轴的负方向。对于每组单胞模型平行界面来说,是一个常数。因此,当应变给定时,公式(4)的等式右侧为一个常值。
本文的单胞模型中浸胶纤维束和基体的形状复杂,因此采用适应性强的C3D4 单元对单胞模型进行网格划分,网格密度为0.2 mm。在ABAQUS 软件中对单胞模型施加载荷为1%位移,随后获取各加载面的总支反力以计算单胞的弹性性能,结果如表3 所示。通过试验研究了2.5D 机织复合材料试样沿X方向(轴向)的压缩弹性模量为24.166 GPa,预测值和试验值的误差为6.06%,证明单胞的预测结果是准确的。

表3 2.5D 机织复合材料单胞弹性性能有限元计算值Tab.3 Finite element calculation values of cell elastic properties of 2.5D woven composites
2.2 宏-细观混合模型的建立
冲击损伤往往呈现出在试样中心“局部”分布的特征[13]。基于此,本文在试样中心区域使用细观模型来分析,边缘区域采用均质模型以减少计算难度。在Micro-CT 扫描结果的基础上重构了不含减纱、含半列减纱和含整列减纱2.5D 机织复合材料的细观模型。细观部分结构主要由接结经纱、纬纱和基体3 部分装配而成,其尺寸为32 mm×20.26 mm×3.6 mm(经向×纬向×厚度)。宏观均质部分则采用与试样相同的规格150 mm×100 mm 进行建模,中间部分留有细观部分孔洞。在ABAQUS 软件中将宏观部分与细观部分装配成一个整体,在细观部分到宏观部分相接区域采用共节点操作进行连接,使应力应变可以在宏观部分和细观部分之间传播。支撑底座为300 mm×300 mm×4 mm的刚体,中间部分留有125 mm×75 mm 的贯穿孔洞,冲头为直径16 mm 的半球形刚体。在模型建立完成后,基于结构力学中的对称性原理[14],将所有模型沿着中心线删去1/2 模型,建立起1/2 有限元模型。通过1/2模型进行研究可以良好呈现复合材料的低速冲击行为,又可以减少网格数量,大量减少计算时间。本文所涉及的3 种试样的低速冲击混合模型如图3 所示。

图3 3 种不同试样的低速冲击宏-细观混合模型Fig.3 Low-velocity impact macro-meso hybrid model of three different specimens
细观部分的材料属性采用浸胶纤维束的计算结果和基体的材料性能,宏观均质部分的材料属性使用2.5D 机织复合材料单胞性能的预测值。将宏-细观混模型的接触设置为通用接触,并建立了接触对来保证冲头表面与试样的合理接触。2.5D 机织复合材料的宏-细观模型内部结构复杂,所以采用和单胞相同的C3D4单元进行网格划分,细观部分网格密度为0.2 mm,宏观均质部分的网格密度为4 mm。在预定义载荷中使用速度定义场,通过给冲头初始速度来对试样进行加载。
2.3 损伤准则与损伤演化
在2.5D 机织复合材料受到低速冲击的过程中,材料往往会出现不同形式的损伤、破坏以及力学性能的下降,而且在冲击侧和非冲击侧材料的破坏会有较大差异。为了在有限元模拟中获得相近的冲击效果,通常需要引入损伤准则和损伤演化规律来判断损伤的起始和发展。
浸胶纤维束通常被视为横观各向同性材料。目前,针对横观各向同性材料常用的损伤准则有Tsai-Wu 准则、Chang-Chang 准则和Hahsin 准则等。其中,Hahsin 准则中参数获取简单且判定形式比较详尽,常被用于浸胶纤维束的损伤判定[15]。树脂基体通常被视为各向同性材料,在复合材料内部起到支撑纤维束的作用,受载方向多变,所以使用各向同性材料常用的Von-Mises 准则作为基体的损伤准则[16]。宏观均质部分结构单一,视作正交各向异性材料,所以本文选用比较简单的最大应力准则[17]作为宏观均质部分的损伤准则,3 种损伤准则的判断公式分别如式(5)、式(9)和式(10)。
浸胶纤维束Hashin 准则:
式(5)中:当σx>0 则纤维拉伸失效
式(6)中:当σx<0 则纤维压缩损伤
式(7)中:当σy>0 则纤维束中的基体拉伸失效
式(8)中:当σy<0 则纤维束中的基体压缩失效。
树脂基体部分Von-Mises 准则:
宏观均质部分最大应力准则:
式(10)中:当σx>0 则一方向拉伸失效
式(11)中:当σx<0 则一方向压缩失效
式(12)中:当σy>0 则二方向拉伸失效
式(13)中:当σy<0 则二方向压缩失效。
式(5)—式(13)中:σi为纤维束的正应力;τij为纤维束的剪切应力;x、y代表方向;S表示截面面积;t 和c 分别为拉伸和压缩。
损伤演化规律如式(14)—式(16)所示:
通过公式(14)和(15)对浸胶纤维束和均质部分中发生损伤的刚度矩阵进行更新。式中:d为损伤因子;C为压缩损伤;G为剪切损伤。下标中1、2、3 代表不同截面方向;f 为纤维束及一方向;m 为浸胶纤维束内基体及二方向。d的默认值为0,满足损伤判定条件时相关参数的具体取值[18]如式(16)所示:
基体部分的损伤演化中,使用刚度折减的方法,材料属性具体折减方法[19]如公式(17)所示:
以上所述的损伤准则和损伤演化规律可通过ABAQUS 用户子程序VUMAT 实现,并结合ABAQUS/EXPLICIT 进行求解。
3 结果分析与讨论
3.1 载荷时间曲线对比
图4—图6 所示分别为54 J 和72 J 的冲击能量下NO-YR、HIN-YR、AIN-YR 3 种试样载荷-时间曲线的数值模拟结果与试验结果。
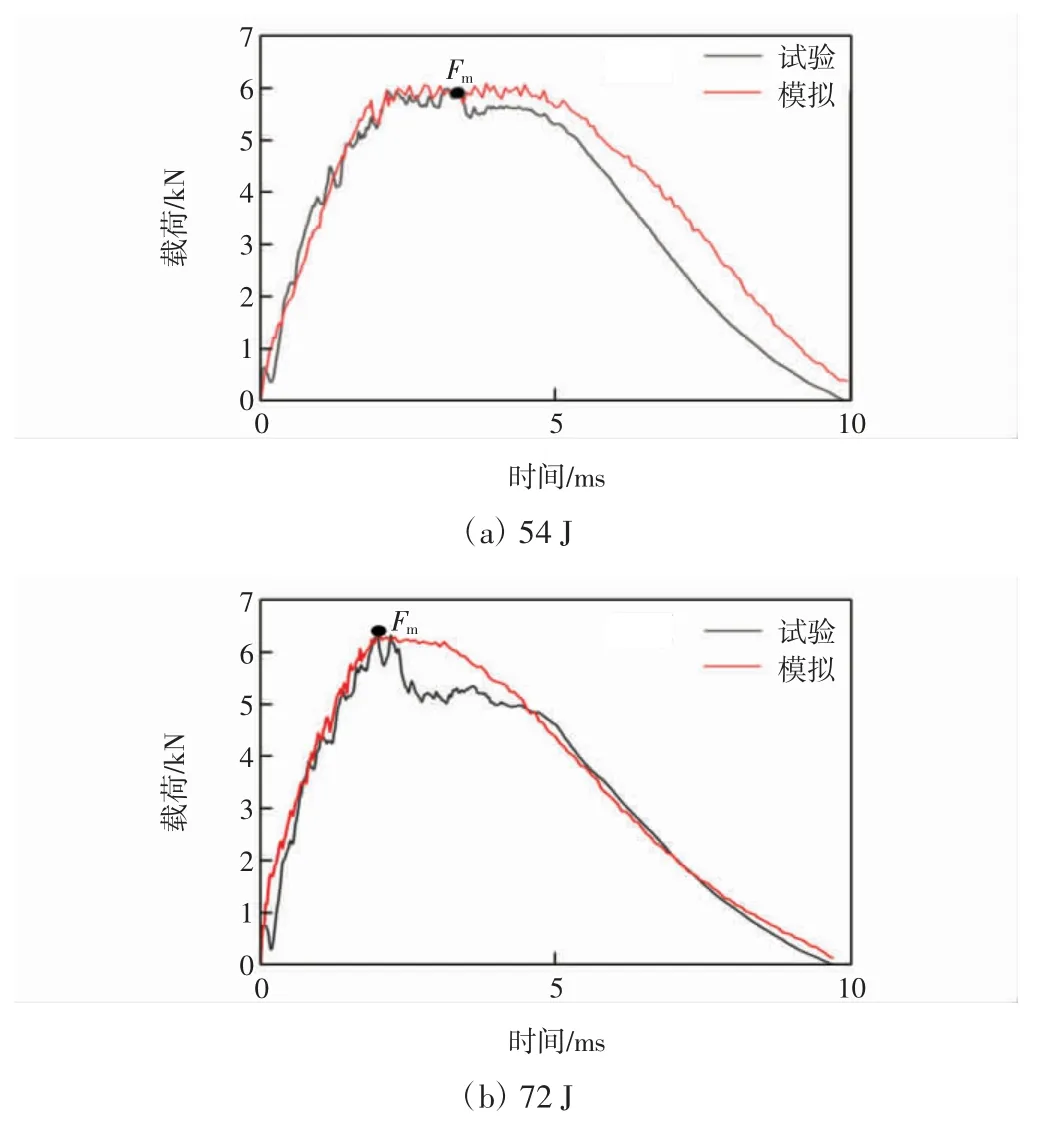
图4 NO-YR 试样低速冲击载荷-时间曲线试验结果与有限元结果对比Fig.4 Comparison of test results of low-velocity impact load-time curve of NO-YR specimen with that of finite element results

图5 HIN-YR 试样低速冲击载荷-时间曲线试验结果与有限元结果对比Fig.5 Comparison of test results of low-velocity impact load-time curve of HIN-YR specimen with that of finite element results
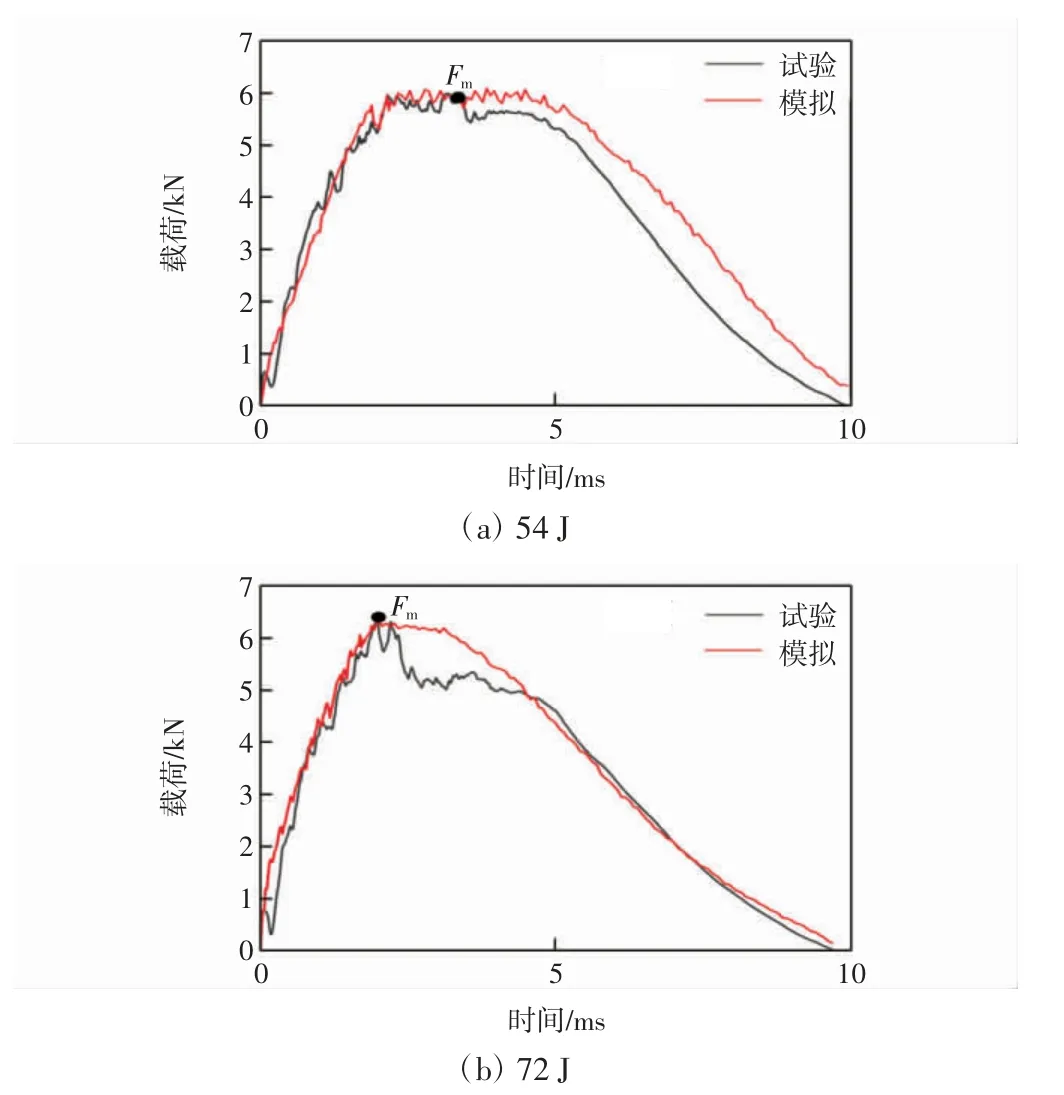
图6 AIN-YR 试样低速冲击载荷-时间曲线试验结果与有限元结果对比Fig.6 Comparison of test results of low-velocity impact load-time curve of AIN-YR specimen with that of finite element results
由图4—图6 可见,有限元模拟结果与试验结果吻合良好。在初始阶段,所有曲线呈现出“近”线性上升。其中,相比于54 J 冲击能量下。试样在72 J 能量下的载荷波动程度略有增加,这就预示着试样中产生了更多的裂纹[20]。随着冲击能量继续增加,在冲击载荷最大值(Fm)附近,曲线波动明显增加,展示出非线性特征。这也意味着试样组份材料承载达到阀值。之后,载荷开始逐渐下降。在此阶段中,试样形变储存的部分弹性势能转化为动能并带动冲头发生回弹[21]。在冲击回弹过程中,试样基本不再产生新的破坏,载荷-时间曲线波动较小。
以上结果证明,有限元模拟结果与实验结果的载荷时间曲线吻合度较高,并且可以比较准确地预测最大载荷位置,验证了宏-细观混合模型的可靠性。
3.2 损伤形貌对比
损伤形貌是评价试样低速冲击行为的另一重要指标。图7 所示为54 J 和72 J 冲击能量下NO-YR、HIN-YR 和AIN-YR 3 种试样的冲击侧(F)和非冲击侧(B)损伤形貌数值模拟与试验对比结果。在之前的报道中,已经有研究证明了低速冲击损伤主要是剪切或者拉伸应力的结果,压缩应力引起的损伤很少[20]。本文中所使用的VUMAT 子程序中未涉及剪切损伤形式,因此,模拟结果选择包含纤维束损伤和基体拉伸损伤SDV7 状态图来表征试样的损伤。其中,红色单元代表失效单元,证明此处产生了破坏。

图7 54 J 和72 J 冲击能量下3 种试样的损伤形貌数值模拟和实验对比Fig.7 Comparison of simulated and experimental damage morphology of three specimen under 54 J and 72 J impact energy
数值计算的试样冲击侧(F)损伤区域及形貌与试验结果较吻合。试样的总体损伤轮廓均呈现出椭圆形,且长轴沿着经纱方向。另外,在损伤边缘区域,基体裂纹呈同心圆弧状分布,如图7(a)、(b)、(g)、(h)所示。在试样的非冲击侧(B),试样主要承受由弯曲变形引起的拉伸应力,所以非冲击侧试样损伤比冲击侧要更加严重[22]。试样的整体损伤轮廓均呈现出沙漏形,且裂纹主要沿经纱方向发展,这说明经纱在试样中起到了主要承载作用。另外,在冲击中心区域,试样以脱粘破坏为主,而在损伤边缘区域,试样则以触须状基体裂纹,如图7(c)、(d)、(i)、(j)破坏为主。与试验结果相近,含不同减纱结构的3 种试样的宏观模拟损伤形貌差距比较微小,这说明本文所提出的混合模型对宏观损伤形貌预测具有比较好的准确性。
通常,在冲击过程中,冲头不断地以弹性应变的形式将载荷传递给试样,一旦试样的变形达到一定程度时,损伤就会产生和发展[20]。因此,可以合理地认为细观模型中产生高应变区域分布与破坏样品中损伤分布相对应。图8 和图9 分别示出了3 种试样在54 J 和72 J冲击能量下的低速冲击模拟中的应变与Micro-CT 扫描的试样内部细观损伤分布的对比图。

图8 54 J 冲击能量下模拟应变与试样内部裂纹分布Fig.8 Comparison of simulated strain and crack distribution inside specimen at 54 J impact energy

图9 72 J 冲击能量下模拟应变与试样内部裂纹分布Fig.9 Comparison of simulated strain and crack distribution inside specimen at 72 J impact energy
从图8 和图9 可以发现,细观模型模拟结果与Micro-CT 形貌中的损伤分布吻合度较高。在细观损伤形貌中可以看到,损伤主要呈纱线交织状的破坏纹路,在模拟结果中的相近位置同样可以发现相似的突起区域,出现这种现象的原因是因为纱线交织点附近区域是复合材料中较弱的部分,容易发生应力集中现象[21]。在54 J 冲击能量下高应变区域分布相对较少,仅从图8(c)AIN-YR 试样的模拟结果中观察到轻微的高应变现象。而在72 J 冲击能量下,模拟结果中的应变分布范围明显增大。从图9(b)中可以看到,在半列减纱区域的模拟结果出现了较低应变,而在纱线全部减少的区域则发生了较大的应变分布。同样从图9(c)AINYR 试样模拟结果中可以观察到较多的高应变区域,这是因为AIN-YR试样中具有更多薄弱的富树脂区域,因此产生了较多的高应变现象[23],说明AIN-YR 试样产生了更多的损伤。
表4 示出了在54 J 和72 J 冲击能量下NO-YR、HIN-YR、AIN-YR 3 种试样的冲击中心区域凹坑深度的试验结果和有限元模拟结果。
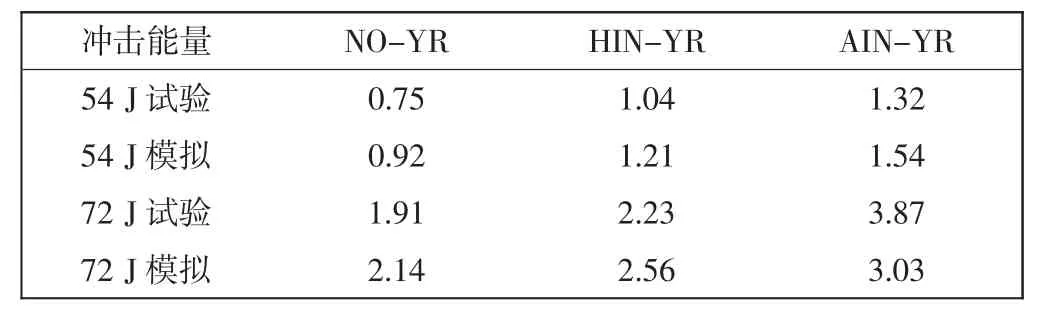
表4 冲击中心凹坑深度试验结果与模拟结果对比Tab.4 Comparison of test results and simulation results of impact center crater depth mm
因为本文应用的损伤准则中未涉及塑性准则,所以有限元模拟结果比试验结果略微偏高。由表4 可见,在相同的冲击能量下,NO-YR、HIN-YR 与AINYR 之间的冲击凹坑深度表现出NO-YR<HIN-YR<AIN-YR 的大小关系。这说明减纱会影响试样整体的损伤分布情况,这与参考文献[24]中的报道具有相似结果。与NO-YR 和HIN-YR 相比,在相同冲击能量下,AIN-YR 会产生更深的冲击凹坑,这与AIN-YR 和HIN-YR 中减去纱线的数量和方式有关。
表5 和表6 分别示出54 J 和72 J 冲击能量下,NOYR、HIN-YR、AIN-YR 3 种试样的损伤体积与损伤率的量化分析结果。
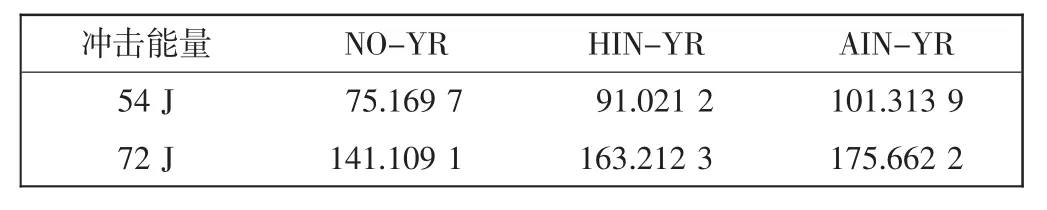
表5 3 种不同试样内部损伤体积Tab.5 Internal damage volumes of three different samples mm3

表6 3 种不同试样内部损伤率Tab.6 Internal damage rates of three different samples %
量化分析基于Micro-CT 数据,通过VG 软件处理完成。由表5 和表6 可见,在54 J 冲击能量下,相比于NO-YR,HIN-YR 和AIN-YR 的损伤体积分别多21.0%和34.8%,损伤率分别比高0.550 3%和0.607 2%。在72 J 冲击能量下,相比与NO-YR,HIN-YR 和AINYR 的损伤体积分别多15.7%和24.4%,损伤率分别高0.439 4%和0.920 3%,3 种试样之间损伤率的差距较明显。其中,AIN-YR 的破坏最为严重,验证了上文的有限元模拟结果。
4 结 论
本文针对锥形回转体构件在近净成形时常用的减纱工艺,选用T700-12K 碳纤维和E-51 环氧树脂,设计和制备了不含减纱、含半列减纱和含整列减纱2.5D 机织碳/环氧复合材料。利用落锤冲击仪,分别设置了54 J 和72 J 的总冲击能量,对3 种不同试样开展了低速冲击试验。获取了3 种试样的冲击载荷-时间响应曲线。并采用Micro-CT 技术开展了3 种试样的损伤机制分析。基于冲击损伤局部分布特征,依据Micro-CT 扫描结果,提出了一种宏-细观混合有限元模型,开展了3 种试样的低速冲击有限元模拟。得到的主要结论如下:
(1)数值模拟的力学响应曲线及损伤形貌与对应试验结果吻合较好。其中,3 种试样在冲击正面和冲背面都呈现出的椭圆形和和沙漏形的宏观损伤形貌,并且破坏区域的边缘呈现出圆弧状和触须状边缘裂纹。
(2)在54 J 和72 J 冲击能量下,相比于不减纱2.5D机织复合材料,含半列减纱试样和含整列减纱试样的冲击损伤体积分别增加了21.0%、34.8%和15.7%、24.4%。结果充分显示,减纱对冲击损伤容限具有明显的抑制作用。
(3)所提出的宏-细观混合数值模型不仅能够准确反应含减纱2.5D 机织复合材料的力学特性和损伤特征,还能够有效地提升计算效率,这为大尺寸复杂结构的计算提供了新思路。

