基于模糊GA算法的创新型产业集群成员选择方法
——以安徽省芜湖高新区新能源汽车产业集群为例
邱璜
(安徽工业经济职业技术学院 机械与汽车工程学院,安徽合肥 230039)
随着我国对环境问题的重视,具有节能、环保优势的新能源汽车产业在各类政策的引导和扶持下,近年来得到了快速发展[1]。从全生命周期来看,新能源汽车产业涵盖电机电控、零部件及整车、动力电池等的研发与制造,以及汽车金融、汽车后服务等多个领域[2-3]。可见,要实现新能源汽车产业技术水平的提升和产品市场竞争力的提高,合理选择产业集群成员则是重要的因素[4]。
在产业集群的研究与评价方面,董磊[5]构建了产业入区评价指标体系,利用Lasso算法模型预处理相关数据,得到各评价指标系数,进而完成对产业集群的划分。可是,由于Lasso算法模型具有多重共线性的特点,当输入特征之间存在高度相关时,倾向于随机选择一个特征,并将其他相关特征的系数设置为零,从而降低了模型的稳定性。梁晨等人[6]根据产业集群特征来划分类簇,运用KMeans算法对类簇进行最小化聚类误差计算,获得集聚水平表征结果。该方法需预先确定簇的数量并选择初始质心。由于初始质心的选择会对最终聚类结果产生较大的影响,因此算法的有效性需要进一步验证。
在参考上述研究的基础上,本文提出一种基于模糊GA算法(Genetic Algorithm,遗传算法)的安徽省新能源汽车创新型产业集群成员选择方法,希望能为地方新能源汽车产业的发展提供帮助。
1 基于泰尔指数嵌套分析法的成员选择需求分析
在对新能源汽车创新型产业集群成员进行选择前,首先需要对该产业的发展情况进行合理分析[7-8]。本文采用泰尔指数嵌套分析法对新能源汽车产业内不同类群与其总体发展的差异进行分析[9]。新能源汽车产业内差异可分为区域间集群差异P( xi)、同类间集群差异P( xij)和单一集群内差异P( xijk)三个部分[10]。通过对集群嵌套式分解计算[11],得到集群在各尺度上的差异;根据差异数值获取各集群在安徽省新能源汽车产业发展总差异中的比重参数[12]。具体算法为:
其中:P 为产业集群对应创新活动的总体差异;P( )xi为产业集群对应创新活动在区域间的差异;P( )xij为产业集群对应创新活动在同类集群间的差异;P( )
xijk为产业集群对应创新活动在自身内部存在的差异;x、xi、xij、xijk分别表示全国新能源汽车产业中各尺度创新发展水平的规模,i 为产业集群、ij 为i 产业集群中的j 发展要素、ijk为i 产业集群中j 发展要素的k 指标参数;y 、yi、yij、yijk分别表示安徽省新能源汽车产业中各尺度创新发展水平的规模。
从式(1)可以看出,新能源汽车产业集群在不同尺度上的规模差异是最能直观体现其集群成员选择目标的参数[13]。为此,本文分别利用变异系数与基尼系数作为测度指标,对新能源汽车产业的创新活动作进一步分析[14]。利用变异系数计算单一尺度上规模与平均值之间的差异,利用基尼系数计算不同尺度间在规模上的差异。根据变异系数与基尼系数的属性,系数的计算结果越大,对应的规模差异也越大。其算式为:其中:c 表示新能源汽车产业的变异系数;表示新能源汽车产业中i 产业集群j 发展要素的k指标参数对应的创新活动规模均值;-x 表示新能源汽车产业中k 指标参数对应的创新活动规模均值;g 表示新能源汽车产业的基尼系数;n 表示新能源汽车产业集群的构成总数。
将新能源汽车产业的变异系数、基尼系数与该产业创新型发展需求之间的偏差,作为集群成员选择的目标参数,结果表示为:
其中:ε 表示集群成员选择需求,也就是后续模糊GA 算法执行的目标;C 和G 分别表示新能源汽车创新型产业发展需求下的理想变异系数与基尼系数。
2 基于模糊GA 算法的产业集群成员选择
鉴于新能源汽车创新型产业集群成员多样化的特征,如果以单一指标对其选择,难以保证产业内外部创新网络的可靠性;因此,需将新能源汽车创新型产业集群成员的选择问题,采用模糊GA 算法转化为对产业变异系数和基尼系数的优化问题。
2.1 模糊逻辑的构建
采用模糊遗传算法对选择范围内的企业组织机构进行分析,将每个企业组织机构的单一指标数据信息作为一个染色体,利用适应度值对其进行划分处理,获取差异数值较大的种群。通过这样处理,能有效避免由于单种类型成员选择较多,而导致的产业集群基因一致化的问题,确保选择结果能够最大限度地实现多样性。由于交叉算子和变异算子对种群内成员构成的多样性有直接的影响,因此构建了模糊逻辑对交叉算子和变异算子进行动态调节;并利用遗传算法的运算方式,将种群的适应度值变化情况设置模糊逻辑,具体表示为:
其中:z( t )表示输入遗传算法中的变量信息,也就是可选择的企业组织数据信息;t 表示遗传算法执行的代数;fmax( t )表示适应度的最大值;favg( t )表示适应度的平均值;fmin( t )表示适应度的最小值。通过该方式对各个染色体进行模糊化处理,为后续成员选择提供可靠的数据基础。
2.2 设置染色体编码
为模糊化处理后的每个染色体设置长度与之匹配的二进制串,采用二进制编码方式对其进行编码处理。对于变量z( t ),定义其指标参数的取值范围均为(0,1);在精度0.001的要求下,z( t )在对应区间离散化的结果可表示为0.001,0.002,…,0.100。利用二进制编码方式对上述数据进行表示时,编码的长度取值结果为5。按照该方式,对每个变量进行二进制编码后,就可以得到由n 个变量构成的企业组织编码信息,对应的编码长度表示为:
其中:d 表示单个可选择企业组织的编码长度;di表示企业组织单个染色体的编码长度。在此基础上,利用浮点数编码的方式将变量z( )t 的指标数据信息映射到遗传算法的分析区间,作为计算适应度值的基础数据。
2.3 模式划分
对编码后的个体按照染色体的构成进行聚类,并以个体为基础单元作初步划分,计算方式为:
其中:κ 表示单一个体在种群中的适应度值;d( z)表示变量z( t )的编码信息;d( Z )表示变量z( t )所在种群的编码信息均值;Z 表示变量z( t )所在的种群。运用公式(10),可将适应度值在种群允许范围内的个体划分到对应的种群中。
2.4 选择操作
为避免寻优结果陷入局部最优,运用轮盘赌选择法对子种群与其适应度值进行匹配;将其中较高染色体所对应的个体作为初代选择,概率表示为:
其中:F ind( z )表示选择算子匹配机制下,种群任意个体被选中的概率;∑Find( Z )表示种群中所有个体被选中的概率之和。
在初代目标种群中,分别计算个体与选择目标间的适应度值,直至种群中个体的适应度不再随着遗传代数的增加而变化,将此时的个体作为最终的选择结果。如此操作,能够确保在成员之间关联的前提下,最大限度弥补当前产业集群构成上存在的短板。
3 测试与分析
3.1 案例选择
安徽省芜湖高新区以奇瑞汽车为龙头,已经形成一定规模的新能源汽车产业集群。奇瑞新能源汽车虽然在产品质量和新能源技术等方面取得了一些成绩,但是其市场占有率仍存在进一步提升的空间。通过对新能源汽车产业发展趋势和消费者购买需求的分析,从创新角度提出芜湖高新区新能源汽车产业集群的优化策略。
近年来,奇瑞新能源汽车的研发投入虽然在持续增长,但是与比亚迪、蔚来等同类企业相比,还是存在着明显差距。研发投入的不足在一定程度上限制了芜湖新能源汽车产业集群的创新发展。动力电池作为新能源汽车的核心构件,其续航性能是新能源汽车重要的研发领域。此外,对电池的回收和循环利用研究,也是新能源汽车产业的重要组成部分。这三方面正是目前芜湖高新区新能源汽车产业集群存在的不足,亟需通过优化产业成员的构成来补齐短板。
3.2 数据的收集与处理
鉴于新能源汽车产业发展中产业链与创新链紧密联系的特点,本研究对芜湖高新区新能源汽车产业集群成员的选择,涵盖了以产品创新为核心的企业、高校及专门的研究机构。在对相关成员进行数据采集时,除了直接可以获取的数据外,对于无法直接获取数据的成员,则借助关系型数据,采用基于提名法的滚雪球抽样方式进行采集。比如,利用组织与芜湖高新区新能源汽车产业集群中重点企业技术部门的技术合作关系进行筛选,对满足要求的组织展开数据调查。为了最大限度地吸纳有实际创新技术和能力的成员,以上述组织为基础,逐级向下做了深入的数据采集。采集数据的内容如表1所示。

表1 数据采集内容
针对滚雪球抽样方法对企业、高校及专门研究机构数据采集深度和广度的不足,按照固定抽样搜索深度,对采集到的数据结果进行剪枝处理,确保统计到的关系型数据具有更高的有效性。最终,筛选出336 个成员单位,涵盖了新能源汽车产业的各个方面。
3.3 测试结果与分析
在上述所得数据的基础上,分别采用本文方法、文献[5]方法和文献[6]方法,对新能源汽车创新型产业集群成员进行选择,并根据所选成员之间的关系,构建起产业集群创新网络。三种方法选择的有效成员数量均为126个,对应形成的产业集群规模也均为126 个。以主要核心成员为基础形成的网络结构如图1所示。其中,网络节点表示成员在集群中的中介性,节点链越多表明中介性越强,即与其存在关联的组织越多。对图1中的网络参数进行统计,得到的数据信息如表2 所示。其中,“边数”是指网络中连接节点间线段的数量;“平均度”是指网络中与节点相连边数的平均值;“密度”是指网络中实际存在边数与可能存在边数的比例;“平均聚集系数”是衡量网络内部连接紧密程度的指标。

表2 不同创新网络的特征参数信息
分析图1、表2所显示的三种选择方法下产业集群创新网络的相关信息可知:运用文献[5]方法构建的网络在平均度上数值明显偏低,这会导致整个网络结构出现一定的偏置,若以此指导新能源汽车产业集群的创新发展,则会引起产业集群内发展的不平衡,直接影响该产业的综合创新能力;运用文献[6]方法构建的网络在边数上相对较少,这就意味着其选择的成员之间合作关系相对较弱,会间接影响新能源汽车产业集群的创新能力;运用本文方法构建的成员网络,边数、平均度、密度和平均聚集系数都是最高的,表明各成员的分布不仅较为平均,而且合作关系也更为紧密,以此指导新能源汽车产业集群的建设,也更能有效促进产业的创新性发展水平。
产业集群在实际运行中,会受到外生性风险和内生性风险的冲击,因此,对所构建创新网络的稳定性进行测度是非常必要的。本文采用仿真模拟的方式,运用Matlab2010b 软件对不同集群创新网络在冲击影响下的动态发展过程进行测度,选取创新网络的“有效规模”和“有效效能”作为测度指标。其中,网络有效规模即产业集群中成员的总数。网络有效效能的计算方式为:
其中:E表示产业集群创新网络的有效效能;γij表示网络中任意两个成员i和j的关联度;G表示产业集群创新网络;N表示产业集群创新网络中有效成员总数。
为最大限度消除随机误差对测试结果的影响,对三种方法构建的创新网络各进行10 次风险动态冲击测试,将10次的均值作为测试结果,数据信息如图2所示。
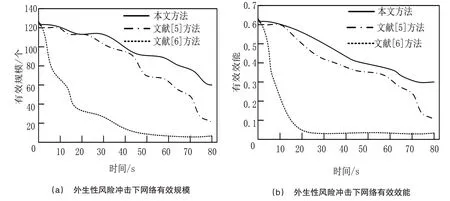
图2 风险冲击下创新网络稳定性测度
从图2 可以看出,随着冲击时间的延长,三种创新网络的有效规模和有效效能均呈下降趋势。其中,运用文献[5]、文献[6]方法构建的网络分别受内生性风险和外生性风险的影响最为明显,而运用本文方法所构建的创新网络在内外部风险的冲击下表现最为稳定。从而表明,运用本文方法选择成员并构成的新能源汽车产业集群,具有较强的风险抵御能力,可以最大限度地保证其创新能力。因此,该方法更符合芜湖高新区新能源汽车创新型产业集群建设对成员选择和产业集聚形态构设的需求。
4 结语
为了增强地方新能源汽车产业在市场竞争中的优势,构建可靠的产业集群至关重要。本文提出了一种基于模糊GA 算法的创新型产业集群成员选择方法,在分析新能源汽车产业发展现状的基础上,设定了产业集群成员的选择目标;借助模糊GA 算法对企业组织与选择目标间的拟合度进行了计算,并根据选择结果构建了新能源汽车产业集群创新网络模式。该模式不仅体现出较高的综合创新能力,而且在不同类型风险的冲击下具有较高的稳定性。本研究可为安徽省芜湖高新区新能源汽车产业集群的创新发展提供有效的参考,也有望在更多类型的产业集群建设和优化中推广。

