面向异构处理平台任务调度的麻雀优化算法

沈小龙,马金全,冀亚玮,谢宗甫,李宜亭,李宇东

(战略支援部队信息工程大学 信息系统工程学院,河南 郑州 450000)

随着时代进步和科学技术飞速发展,信号处理应用对处理器性能要求越来越高。由于传统单一信号处理平台已经不能满足当前需求,因此异构处理平台应运而生,其内部包含丰富的处理器类型[1-2],能够满足不同信号处理应用的需求。信号处理应用通过有向无环图(Directed Acyclic Graph,DAG)[3-4]抽象为任务集合,然后通过调度算法将任务分配到各处理器执行,当前调度算法[5-7]对任务执行的实时性关注较多,均以调度长度为优化目标,造成处理器负载失衡,因此异构处理平台中的负载均衡调度算法具有重要研究价值。

文献[8]提出麻雀搜索算法(Sparrow Search Algorithm,SSA),通过麻雀捕食与反捕食机制解决数学中求取极值问题。SSA算法因具有较强全局寻优能力故在电力系统和神经网络等领域得到广泛应用。文献[9]对SSA算法中的发现者位置更新做出改进,从跳跃式优化为移动式,所提算法对网络的权值参数进行优化,提高了电力负荷预测准确度。文献[10]在麻雀种群初始化时采取Logistic混沌映射提高初始种群质量,得到较优解后采取随机游走扰动策略提高全局搜索能力,减小了电力负荷预测误差。文献[11]利用遗传算法对麻雀位置更新规则进行改进,利用模拟退火算法避免陷入局部最优,所提算法在车间调度问题中取得了较好的调度结果。文献[12～13]利用SSA算法对BP神经网络的权值和阈值参数进行优化,提高了网络稳定性和准确性。

由于SSA算法在异构处理平台任务调度领域研究较少,因此本文提出一种面向异构处理平台的麻雀优化算法(Heterogeneous Processing platform Sparrow Optimization Algorithm,HPSOA),该算法对SSA算法进行优化,设计了离散任务分配到连续麻雀位置信息的编解码规则,改善了麻雀位置更新计算式,并制定符合优化目标的适应度函数。

1 系统模型

异构处理平台总体分为4层[14-15],如图1所示。底层为硬件层,包含平台所有处理器资源;底层之上为中间层,由操作系统层、板级支持包和平台抽象层等组成;中间层之上为组件层,包含项目组研发的所有组件;顶层为应用层,包含当前平台部署的信号处理应用程序。当异构信号处理平台增加新应用时,首先进行功能分析,从组件库中挑选组件搭建应用程序;之后利用调度算法为应用程序中组件分配处理器;最后通过中间层将组件部署到相应处理器,完成新应用程序在异构处理平台的开发。

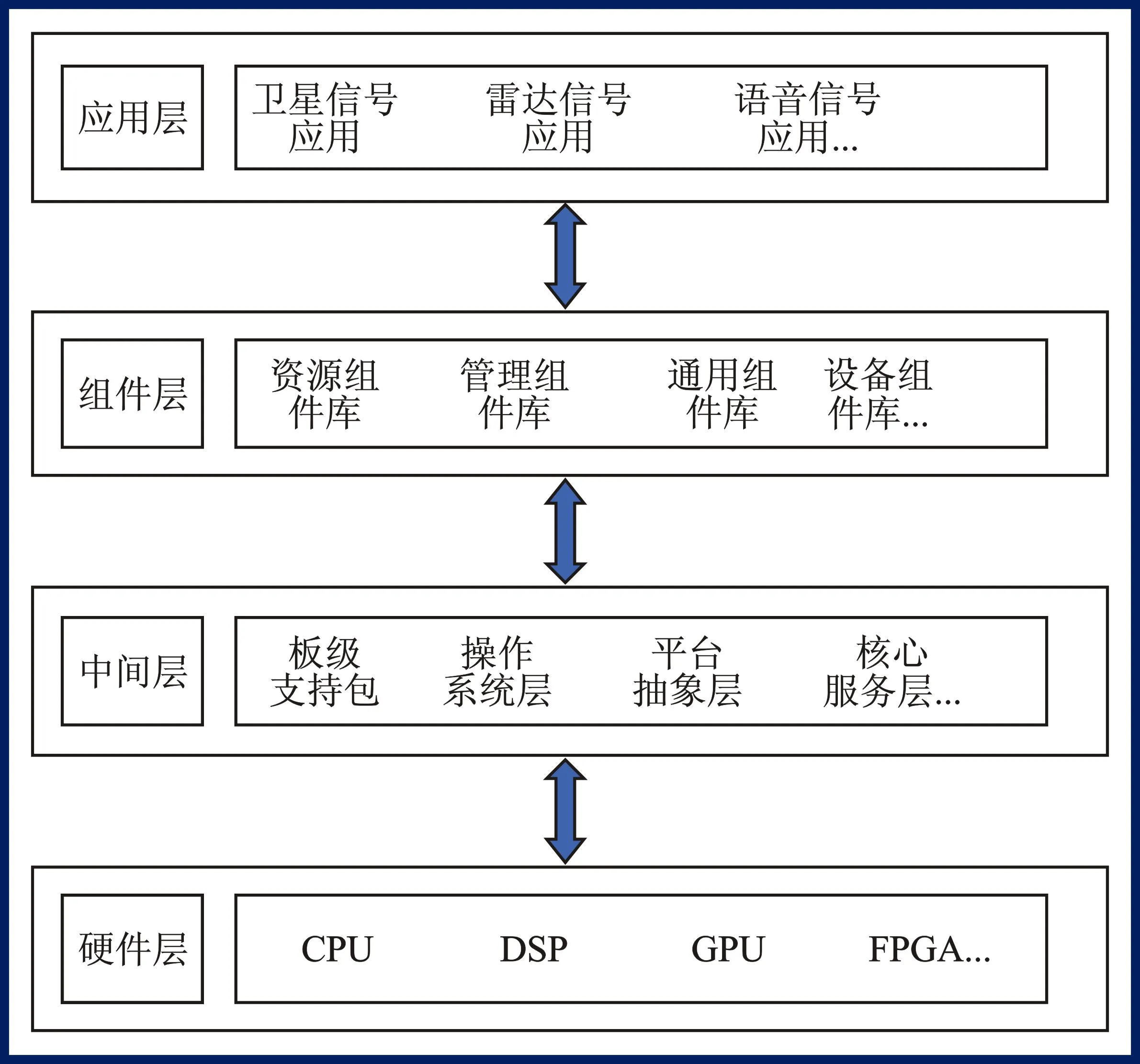
图1 平台结构Figure 1. Platform structure

调度算法决定各应用完成时间和处理器分配任务情况,对系统整体实时性和各处理器工作效率影响较大,因此调度算法较为重要。在调度问题研究中,将应用程序抽象成DAG图,定义为G=(V,C,P,W)。经典DAG如图2所示。vi为任务,与图中节点对应,cij为任务间平均通信开销,与图中有向边对应,pi为处理器,wij为任务在处理器上计算开销,与表1对应。

表1 典型DAG计算成本

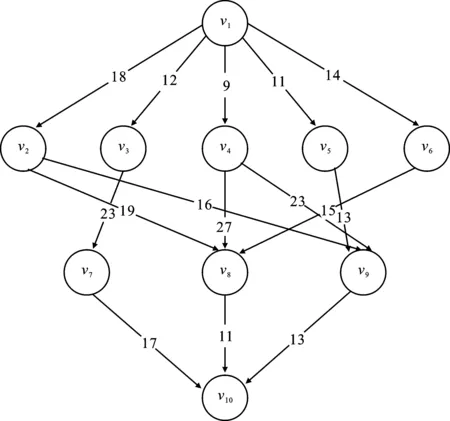
图2 典型DAG任务图Figure 2. Typical DAG task diagram

2 HPSOA算法

2.1 算法思想

当麻雀进行觅食时,根据麻雀适应度函数值将种群内部分为发现者、跟随者和警戒者。经典SSA算法中适应度函数值表示麻雀和食物之间的距离。

发现者处于种群领导位置,具有较强觅食能力和搜索能力,能够引导其他个体在当前局部最优范围进行搜索。发现者还具有较高的反捕食能力,当报警值超过安全阈值时,会向麻雀较多地方移动,以此来降低自身被捕食的风险。

跟随者是种群中数量最多的群体,大部分麻雀会在发现者确定的局部区域进行搜索,寻找当前区域内的最优解。其他个体因为距离当前区域食物源位置较远,故选择逃离当前区域,寻找新的觅食区域。因此,发现者和跟随者的划分并不是一成不变,两者中的个体能够进行角色转换。

警戒者是将种群中所有麻雀按照一定数量比例随机选取,所以有发现者也有跟随者。当警戒者意识到危险时,引导种群离开当前区域到更广泛区域搜索,有利于跳出局部最优,寻找全局最优解。

2.2 算法建模

将异构处理平台中应用程序抽象为DAG任务图后,任务调度算法负责将各任务分配到处理器,属于离散问题。麻雀算法最初是求解极值问题,属于连续问题,因此建立合适的模型将麻雀算法应用到任务调度领域较为重要。

本文将每只麻雀建模为任务调度算法的一种分配方案,建模计算式为

(1)

其中,n表示待分配任务数;m表示麻雀数量;pop21表示第2只麻雀为任务1分配的处理器;若有p个处理器,则pop中每个值有p种可能,因此任务调度问题被转换为麻雀搜索问题。

2.3 任务优先级排序

麻雀为每个任务分配处理器后,任务调度顺序较重要,由于优先级排序不同,因此调度结果差别较大。当前任务调度算法中优先级排序策略单一时,不同类型任务采用相同排序方法,未分析各类型任务之间的差别,这将导致排序结果不准确。针对该问题,本文采用任务优先级分流排序策略。

根据任务图通信计算比,将任务图分为计算密集型和通信密集型任务,对于通信密集型任务,其优先级排序计算式为

(2)

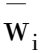
计算密集型任务的优先级排序计算式为

(3)

其中,σi为任务i在3个处理器上计算成本标准差。利用计算成本标准差可得到符合计算密集型任务排序方法,并将对任务序值降序排序后的结果作为最终调度顺序。

2.4 适应度函数

针对处理器负载不均衡问题,本文优化目标为处理器负载均衡指数(processor load,pld),其计算式为

(4)

makespan(m)=EFT(m,vexit)

(5)

其中,EFT(m,vexit)表示麻雀m分配方案中出口任务完成时间,调度长度值越小越好。

本文将调度长度和处理器负载均衡指数的组合作为最终适应度函数,但二者数值相差较大,因此不能直接相加。为使二者处于相同衡量水平,首先进行归一化处理,pld计算式为

(6)

其中,max(pld)为本次迭代负载均衡指数最大值;normal_pld(m)表示麻雀m归一化后的负载均衡指数。

makespan的计算式为

(7)

其中,max(makespan)为本次迭代调度长度最大值,表示麻雀m归一化后的调度长度。

适应度函数计算式为

fitness(m)=normal_pld(m)+normal_makespan(m)

(8)

得到适应度函数值后,按降序排序作为麻雀种群分工依据,将排序靠前的麻雀作为发现者,其余作为跟随者,随机选取警戒者。

2.5 编码规则

麻雀算法在连续问题求解中运用广泛,而任务调度问题是离散化问题,将麻雀的位置更新计算式运用到任务分配方案中是关键问题。针对该问题,本文提出二进制异或编码规则,将任务分配方案映射成连续位置信息。

以经典DAG任务图为例,对编码规则进行介绍。当麻雀确定好任务分配处理器后,按照任务优先级排序顺序计算其分配方案的适应度函数值,然后进行位置编码,图3为其编码过程。

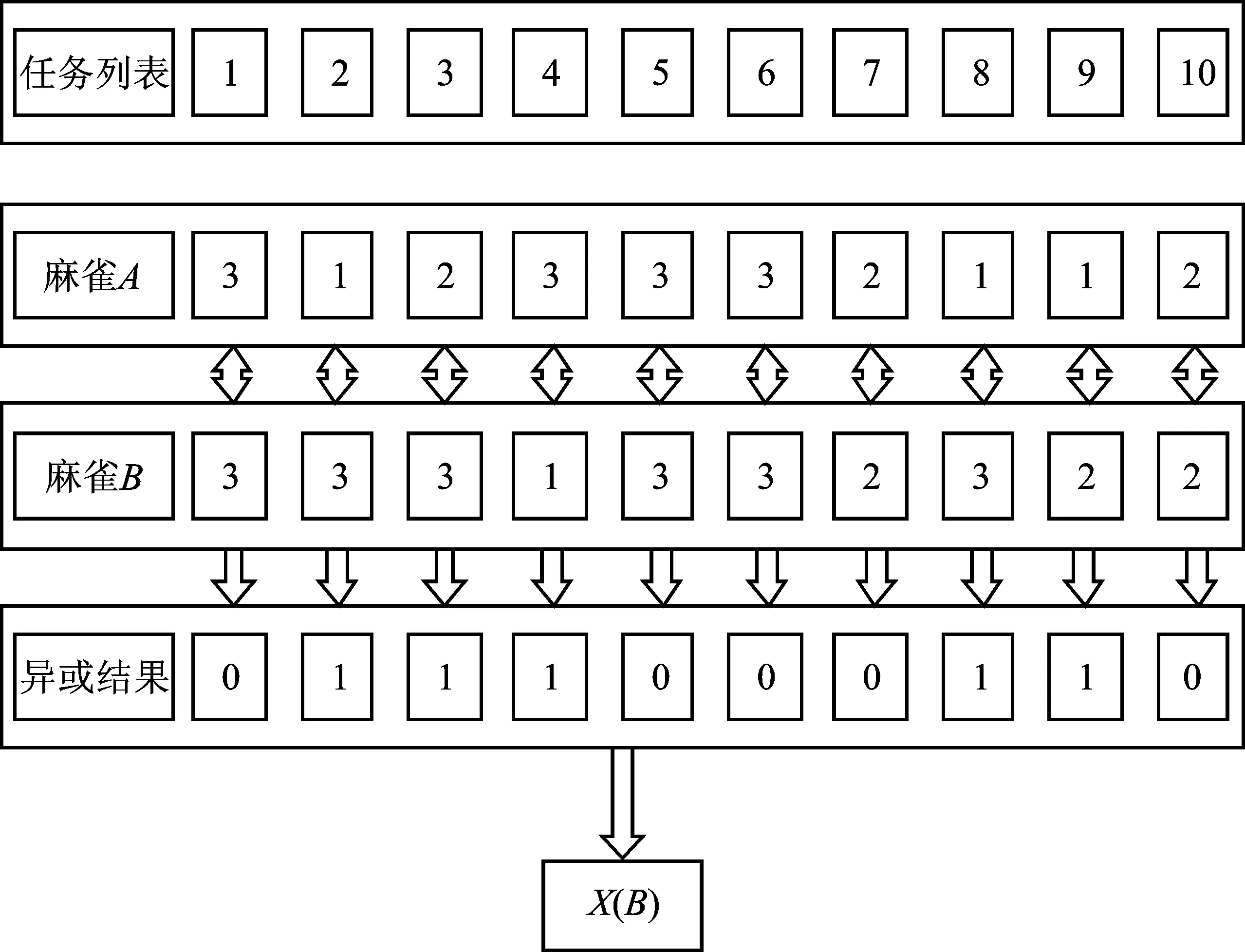
图3 编码过程Figure 3. Coding process

其中,麻雀A在本次迭代中适应度函数值最优,因此将其分配方案作为参考基准,在计算麻雀B位置信息时,采取异或思想。将麻雀B分配方案同麻雀A逐任务对比,然后将对比结果转换为十进制数作为其连续位置信息,其余麻雀均按照此规则计算。

2.6 位置更新规则

在每次迭代中计算麻雀适应度函数,按其降序对种群分工,然后根据编码规则计算麻雀位置信息,最后根据不同更新规则计算更新后的位置信息。

发现者是处于位置较好的麻雀,具有较优适应度函数值,其位置更新计算式为

(9)

其中,Xi(t+1)表示麻雀i迭代后的位置信息;safe为安全阈值,取值范围是(0.5～1.0);rand是报警值,取值范围为(0～1);K为服从标准正态分布的随机数;genmax是最大迭代次数。

跟随者是数量最多的群体,其适应度函数值较差,其中前半部分的位置更新计算式为

Xi(t+1)=Xbest(t)+|Xi(t)-Xbest(t)|×A

(10)

其中,Xbest(t)表示本次迭代中最优位置;A取值为-1或1,后半部分因位置较差,需重新分配处理器。

警戒者位置更新计算式为

(11)

其中,fit(best)和fit(worse)分别是适应度函数的最优值和最差值;rand是服从标准正态分布随机数;B是介于[-1,1]的随机数;β是一个较小的数,用以保证分母不为0,其取值需同适应度函数值的差值保持相同数量级。

得到新位置信息后,将该数据转换为二进制数,找到值为1的任务,对其处理器进行随机选择,作为更新后分配方案。HPSOA算法的运行流程如图4所示。

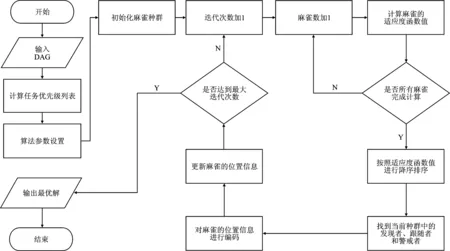
图4 HPSOA运行流程Figure 4. HPSOA operation flow

3 仿真实验及性能分析

设计仿真实验将HPSOA算法同ICPA[4]进行对比,验证算法有效性和可靠性。

表2为仿真实验平台信息,表3为算法参数设置,其中m为麻雀种群数量,genmax为迭代次数,safe为安全阈值,N_discover为发现者比例,N_vigilant为预警者比例。

表2 仿真平台信息

表3 HPSOA算法参数设置

3.1 算法有效性分析

为验证本文算法有效性,设置两组实验进行对比,实验1是经典任务图,实验2是随机任务图。

实验1将经典任务图用ICPA和HPSOA算法分别进行调度,得到HPSOA适应度函数变化如图5所示,HPSOA调度长度如图6所示,ICPA负载情况如图7所示,HPSOA负载情况如图8所示。

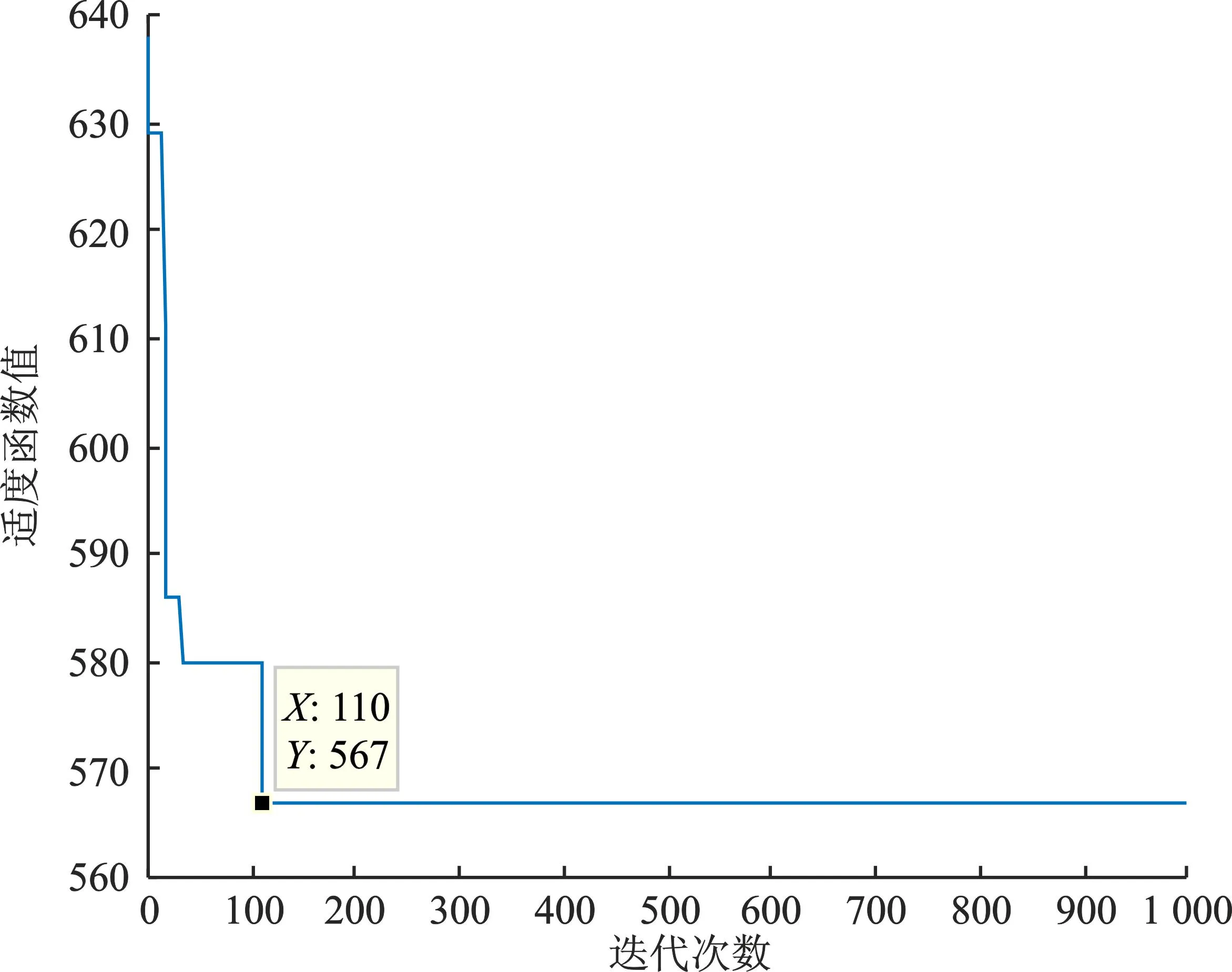
图5 HPSOA适应度值变化(实验1)Figure 5. Change of HPSOA fitness value(experiment 1)

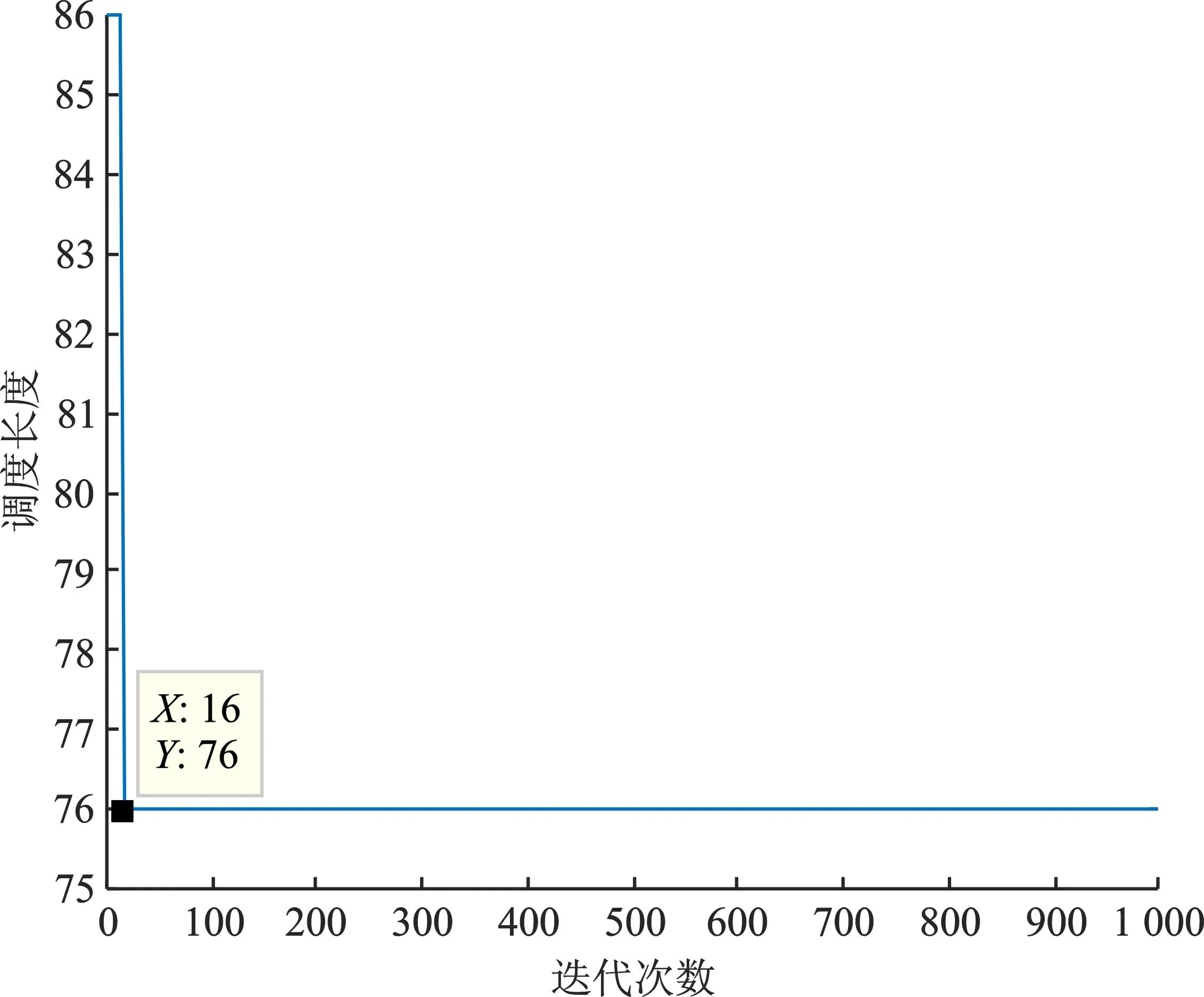
图6 HPSOA调度长度变化(实验1)Figure 6. Change of HPSOA scheduling length(experiment 1)

图7 ICPA负载情况(实验1)Figure 7. Load of ICPA(experiment 1)

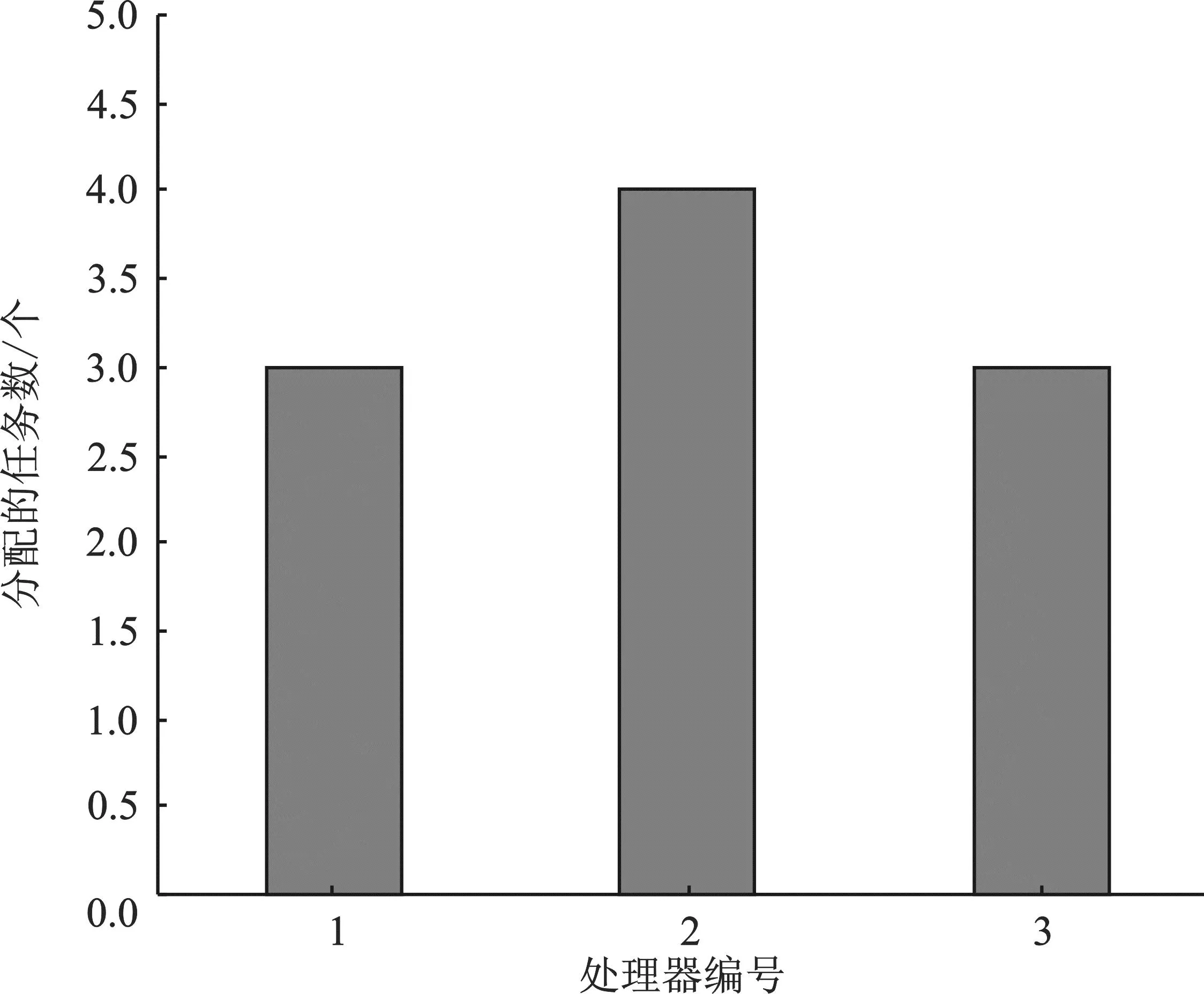
图8 HPSOA负载情况(实验1)Figure 8. Load of HPSOA(experiment 1)

仿真得到ICPA调度长度为67,HPSOA为76, HPSOA调度长度小于ICPA是因为其优化目标为负载均衡,调度长度性能有所牺牲。

仿真得到ICPA负载均衡指数为0,HPSOA负载均衡指数为0.471 4。其中ICPA总任务数为12,是因为在两个非关键处理器上进行了任务复制。该实验中任务数较小,未发挥出算法的性能优势,HPSOA的负载均衡劣于ICPA。

实验2应用DAG随机生成程序生成一个任务数为20、处理器数为4的DAG任务图,仿真得到HPSOA适应度函数变化如图9所示,调度长度如图10所示,ICPA负载情况如图11所示,HPSOA负载情况如图12所示。

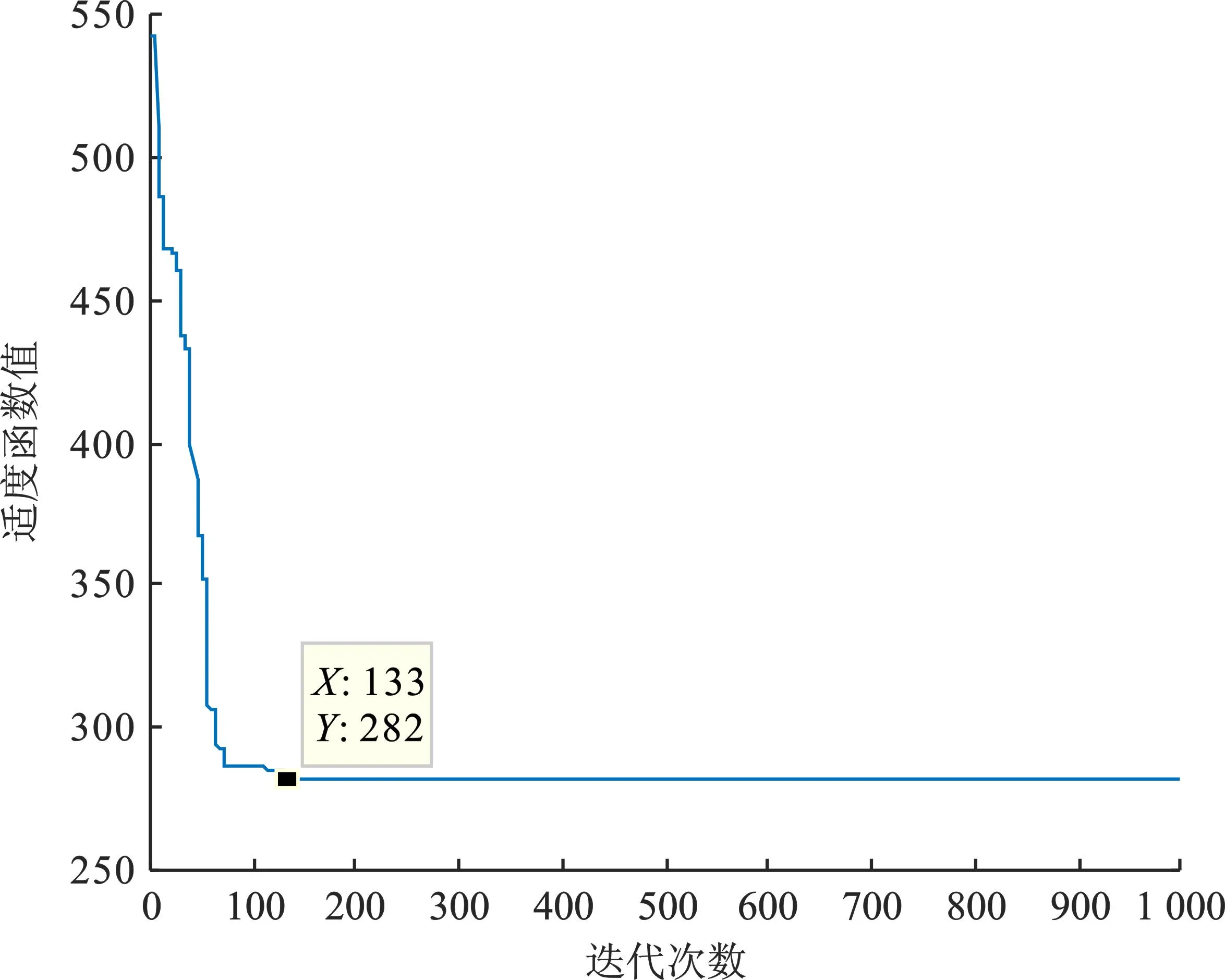
图9 HPSOA适应度值变化(实验2)Figure 9. Change of HPSOA fitness value(experiment 2)

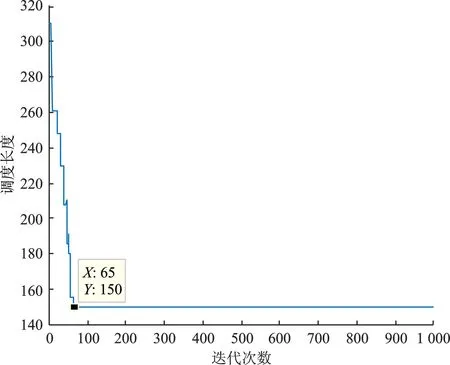
图10 HPSOA 调度长度变化(实验2)Figure 10. Change of HPSOA scheduling length(experiment 2)

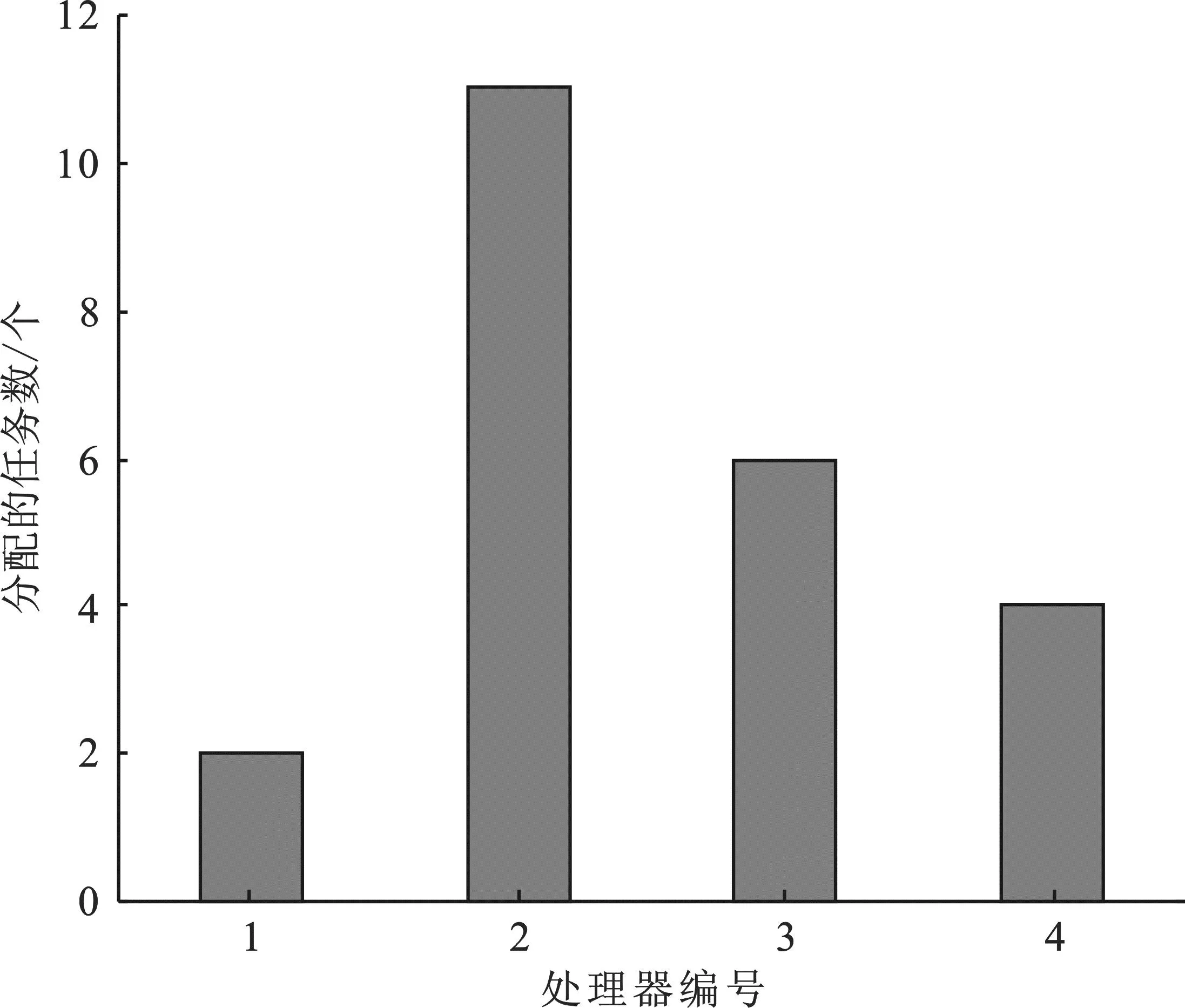
图11 ICPA 负载情况(实验2)Figure 11. Load of ICPA(experiment 2)

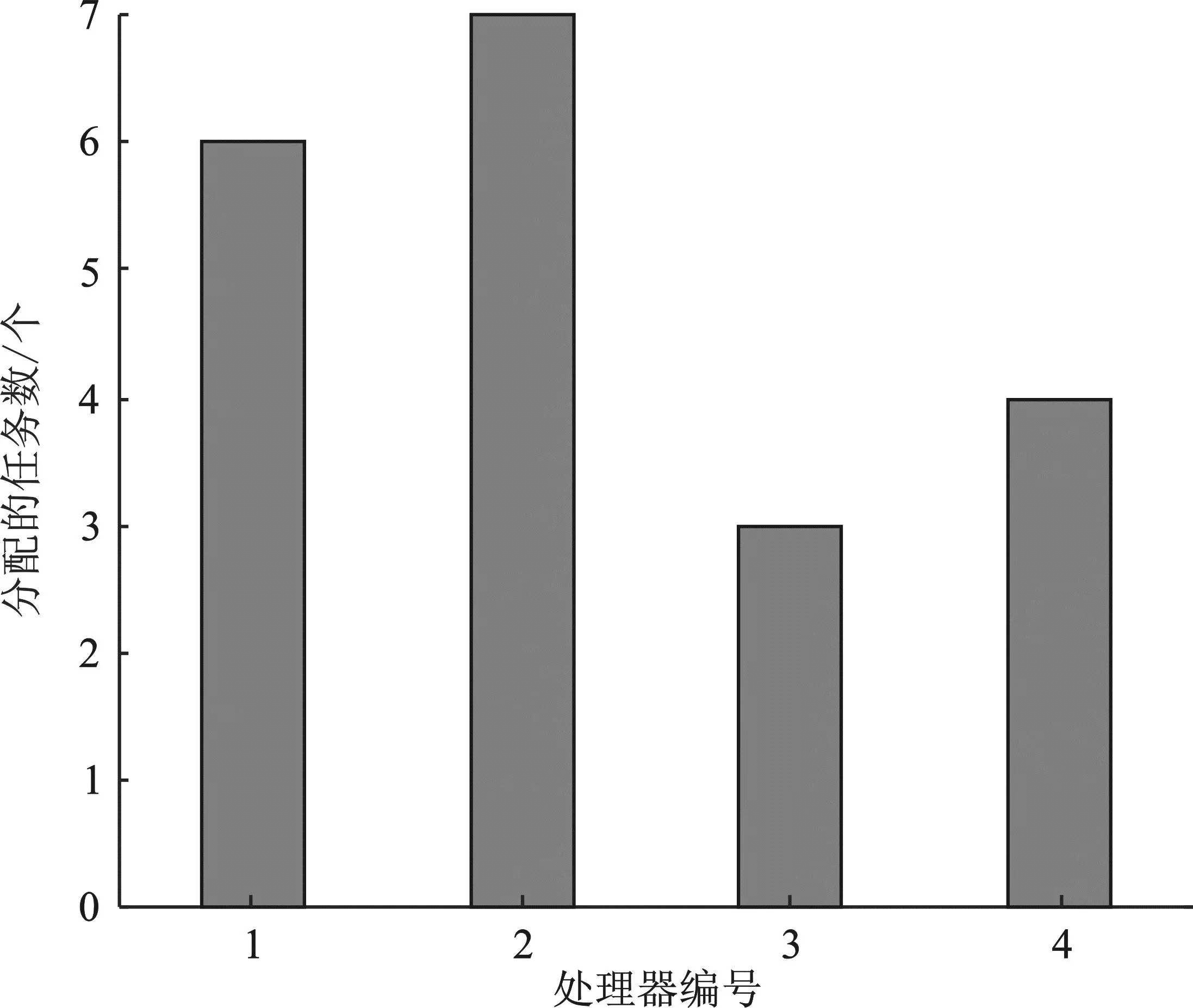
图12 HPSOA 负载情况(实验2)Figure 12. Load of HPSOA(experiment 2)

仿真得到ICPA调度长度为136,HPSOA调度长度为150,ICPA负载均衡指数为3.344 8,HPSOA负载均衡指数为1.581 1,该实验中ICPA算法的3个非关键处理器进行了任务复制。从仿真实验结果可以看出,HPSOA算法相比于ICPA算法,在牺牲一定调度长度性能后,处理器负载均衡性明显提升。

从以上两个实验得出,HPSOA算法适应度函数值曲线均趋于收敛,说明算法中对于编码规则和位置更新规则的改进有效。对随机生成的任务图,处理器负载均衡性能改进明显,证明了算法的有效性。

3.2 算法可靠性分析

为验证算法可靠性,本文设置两组实验进行对比,与实验1中任务图处理器数相同,与实验2中任务图任务数相同。

实验3利用随机DAG程序生成一组处理器数为5、任务数为40、60、80、100任务图,进行仿真实验,得到ICPA和HPSOA的调度长度对比如图13所示,负载均衡指数对比如图14所示。

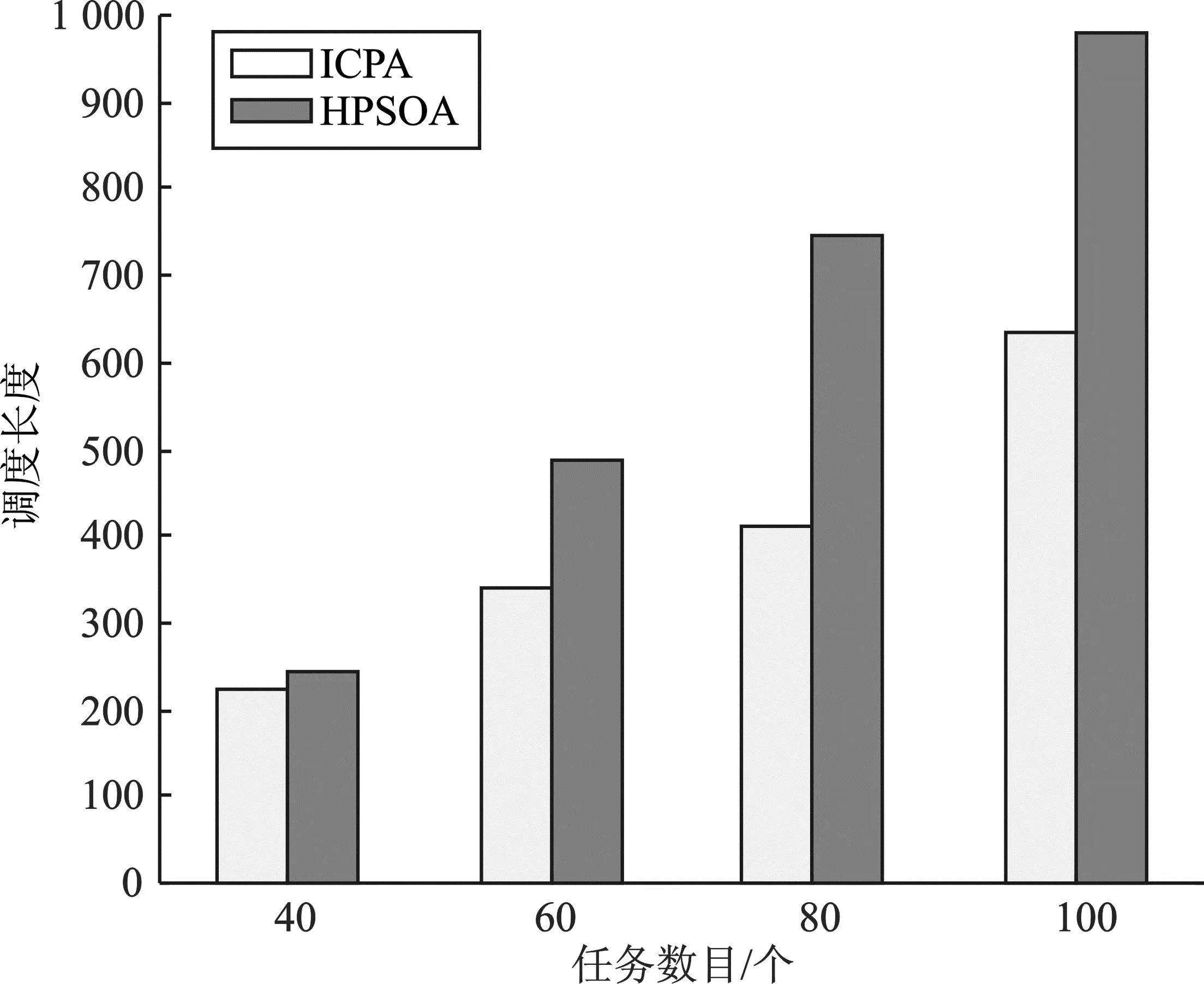
图13 调度长度对比(实验3)Figure 13. Comparison of scheduling length(experiment 3)

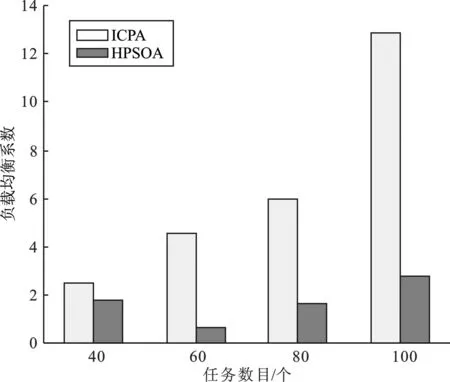
图14 处理器负载均衡指数对比(实验3)Figure 14. Comparison of processor load balancing coefficients(experiment 3)

从图13～图14可以看出,HPSOA算法在牺牲调度长度性能后,其负载均衡指数均优于ICPA。

对随机任务图的调度结果进行计算可知,该实验中调度长度平均牺牲率为46.90%,负载均衡指数平均优化率为66.09%。

实验4利用随机DAG程序生成一组任务数为20、处理器数为4、5、6的任务图,进行仿真实验,得到ICPA和HPSOA的调度长度对比如图15所示,负载均衡指数对比情况如图16所示。

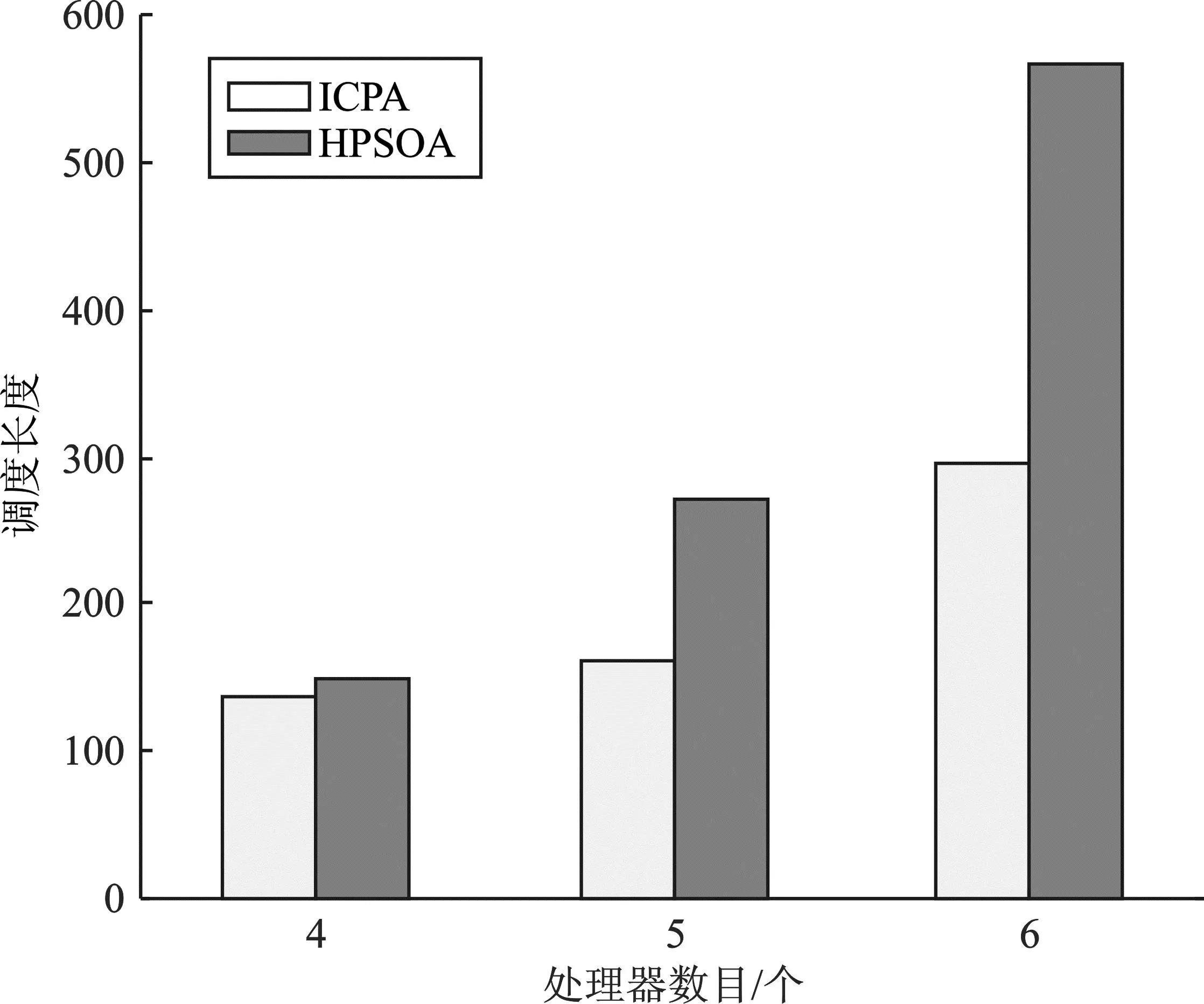
图15 调度长度对比(实验4)Figure 15. Comparison of scheduling length(experiment 4)

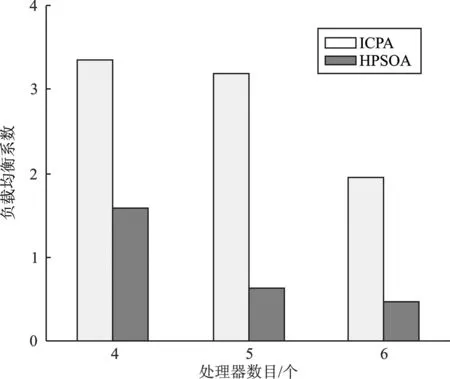
图16 处理器负载均衡指数对比(实验4)Figure 16. Comparison of processor load balancing coefficients(experiment 4)

从图15～图16可以看出,HPSOA算法在牺牲调度长度性能后,其负载均衡指数均优于ICPA。对调度结果进行计算得到,该实验中调度长度平均牺牲率为56.13%,负载均衡指数平均优化率为69.57%。

实验3中任务平均数为70,处理器数为5;实验4中任务数为20,处理器平均数为5。从以上两组实验结果中看出,随着任务数目增多,相比于ICPA算法,HPSOA调度长度牺牲率从56.13%降到46.90%,负载均衡指数优化率稳定在60%左右。随着任务数目增多,HPSOA调度长度牺牲率越来越小,负载均衡优化率依旧稳定,证明了该算法的可靠性。

4 结束语

针对异构信号处理平台中各处理器负载差异较大问题,本文提出了一种面向异构处理平台的麻雀优化算法。该算法在SSA算法基础上提出了适合任务调度分配的编码规则,制定了求取最优化的适应度函数,并对位置更新规则进行改进。通过仿真实验可知,相比于ICPA算法,HPSOA算法的负载均衡指数优化效果明显,能更好地发挥每个处理器效能,提升平台整体工作效率。