基于休止角试验的颗粒钾肥离散元模型参数标定

周 滨,周 岭,万 畅,,谭 彧,何义川,王海刚,谭小华

(1.塔里木大学 现代农业工程重点实验室,新疆 阿拉尔 843300;2.中国农业大学 工学院,北京 100083)

0 引言

EDEM是以离散元法为基础的应用型软件,可以快速、简便地建立颗粒系统的参数化模型,添加颗粒的力学性质、物料性质和其他物理性质[1]。近年来,越来越多的科研人员应用该软件研究散体颗粒的物理特性[2-4]。颗粒肥料作为影响农产品产量和质量的重要因素之一,全面系统地了解其物理特性,有助于施肥机械的优化和研究[5]。

在应用EDEM软件进行仿真前,需要对散体颗粒的物理特征参数(三轴尺寸、密度等)和接触力学参数(泊松比,剪切模量、碰撞恢复系数、摩擦因数)进行测定。余参参、吴孟宸、张锐等人通过使用直接测量的方法测出了物料的剪切模量和泊松比等物理参数[6-8]。然而,物料间的接触参数很难通过相关仪器直接测量获得。有人尝试将物料平铺并固定在斜面上,然后让物料在此斜面上滚动,以此获得物料间的接触参数[9-11]。但是,物料在斜面滚动时会与固定在斜面的物料产生碰撞,所以用这种方法获得的接触参数会有比较大的波动[12-13]。因此,有学者提出了虚拟标定试验确定仿真中所需的参数。Coetzee、Grima等人通过虚拟标定法获得了物料间的接触参数[14-15]。虚拟标定法的优点在于此法所获得的参数具有一定的参考价值,但存在效率低、无标准化等缺点。因此,为了弥补这种方法的不足,有学者提出了离散元仿真标定的方法[16]。温翔宇、刘彩玲等人通过爬坡试验对不同堆积方法下的休止角具有显著影响的参数进行了标定,确定了尿素间的摩擦因数[17-18]。李铁军[19]对煤颗粒模型接触参数进行了Plackett-Burman(PB)试验设计和单因素试验设计,得到了各接触参数对堆积特性的因素显著性及显著性排序。本研究采用无底圆筒法获取钾肥颗粒的休止角,通过Plackett-Burman、最陡爬坡以及Box-Behnken试验对离散元参数进行标定,对试验值和仿真值进行对比验证,旨在为钾肥颗粒离散元仿真参数提供参考。

1 材料与方法

1.1 颗粒钾肥基本参数测量及选取

由于肥料种类繁多,不同的肥料之间的各基本参数、成分都有差异。从外观上来讲,不同肥料的形状大小差异也很明显,有球状、近球状、不规则形状等。本次研究采用的是颗粒状黄腐酸钾有机肥(生产厂家中海石油化学股份有限公司,制造标准GB/T 10205-2009),大多是近球状,颗粒体积较小,含水率小于0.5%。

1.1.1 三轴尺寸与质量的测量

为了使测量的三轴尺寸和质量具有随机性,从50kg钾肥中随机抽取500粒肥料进行三轴尺寸及质量的测量。测量仪器分别是游标卡尺(精度0.02mm)、电子天秤(精度0.0001g),如图1所示。测三轴尺寸时,分别测量颗粒的长、宽、高3个方向[8],测量时,分别选取每个方向上的两个顶点进行测量,并记录数据。在进行质量测量时,先将天秤归零,等读数稳定在零时,从侧面将钾肥颗粒放进天秤中,等读数稳定在某一数值时,进行读数,并记录下来。

图1 游标卡尺和电子天秤Fig.1 Vernier scale and electronic scales

钾肥的三轴尺寸分布及质量分布统计如图2所示。图2中,质量为0.03～0.05g的钾肥颗粒最多,约占40%;整体质量分布在0.02～0.08g之间。颗粒的长度大多分布在4～6mm之间, 5～6mm的占比最高,占23%;宽度大多分布在1.5～3mm之间,宽度为2.5～3mm的占比最高;高度大多分布在3～4.5mm, 3.5mm的占比最高,约为20%。通过对图2的分析可知:钾肥颗粒整体呈椭圆形,且椭圆的长轴为6mm,短轴为3mm左右。

1.1.2 密度测量

通过排液法测量钾肥的密度。用精度为0.01g的电子天秤随机选取70g钾肥,采用量程为250mL的量筒对钾肥进行密度的测定,试验重复5次,测量结果选平均值,最后测得钾肥的密度为1520kg/m3。通过查阅相关文献[10,16]确定其他离散元参数,如表1所示。

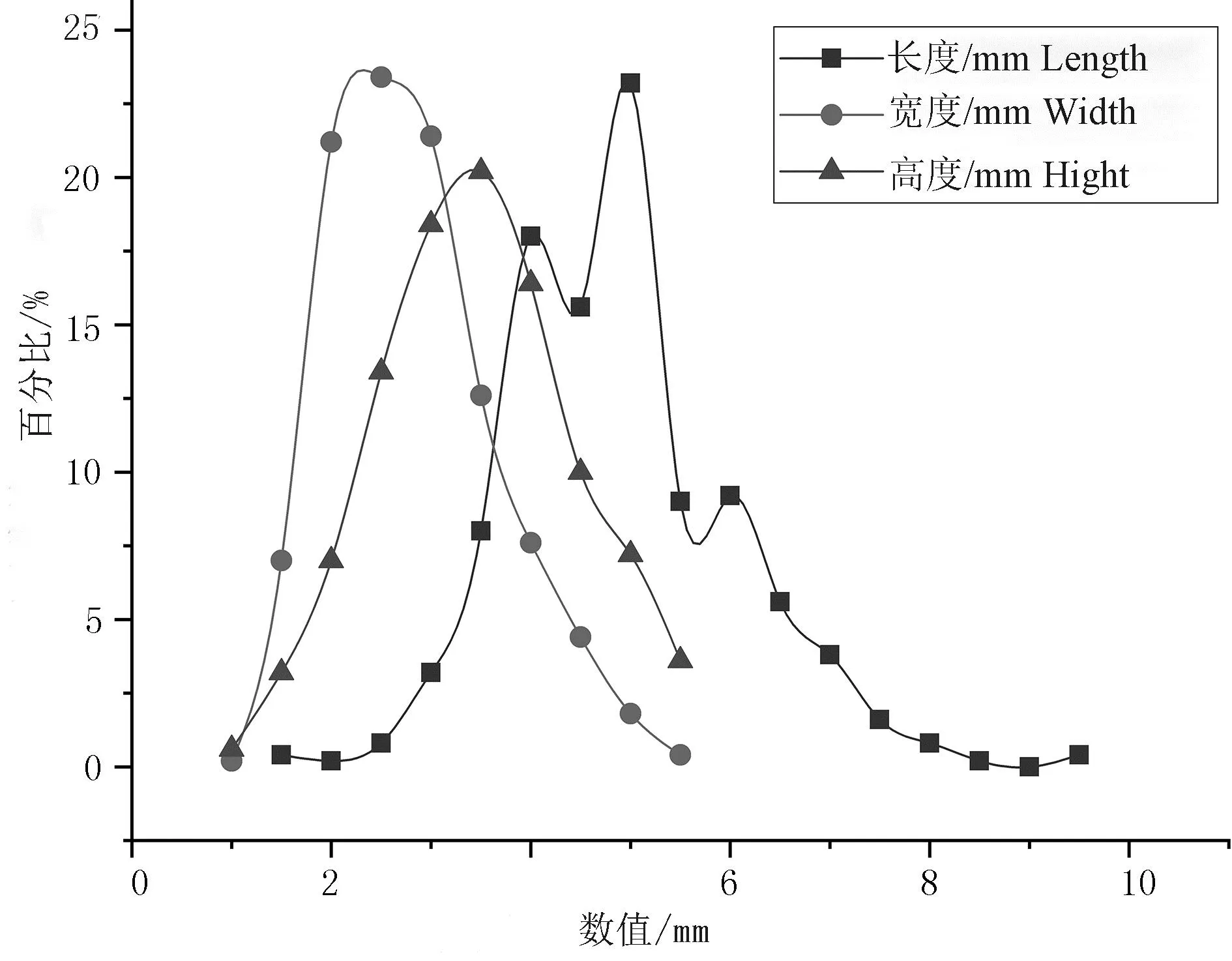
(a) 三轴尺寸概率分布

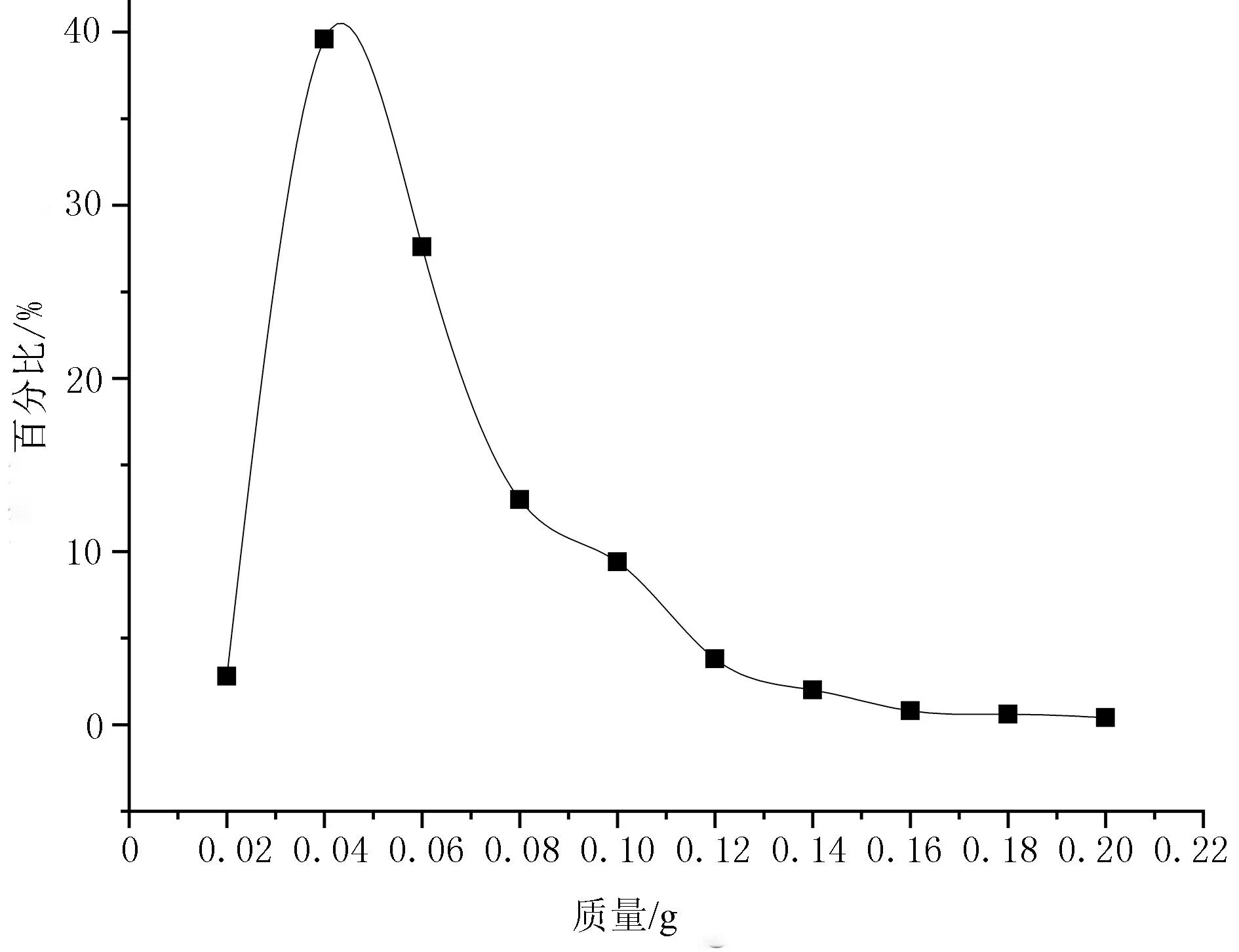
(b) 质量概率分布图2 钾肥三轴尺寸和质量概率分布Fig.2 Probability distributiong of triaxial dimensions and weight

表1 离散元仿真参数取值及取值范围Table 1 Parameter value and range of discrete element simulation

续表1

1.2 休止角堆积物理试验

在本次无底圆筒堆积试验中,使用的圆筒及底板均为钢板。圆筒内径98mm、高220mm,底板是长为400mm的正方形板。测量时,将无底圆筒和底板水平放置,通过万能实验机以0.05m/s速度提升圆筒,等所有颗粒与无底圆筒分离并在底板上形成近似锥形的颗粒堆时测量颗粒堆与底板形成的角度,所得的角度即颗粒钾肥的休止角,如图3所示。重复5次试验,得到休止角的平均值为21.64°。

图3 颗粒钾肥堆积试验Fig.3 Accimulation test of poisson

1.3 休止角仿真试验

1.3.1 颗粒钾肥离散元仿真模型

根据对钾肥三轴尺寸的分析,钾肥的模型是长轴为6mm、短轴为3mm左右的椭圆,如图4所示。在建立钾肥模型时,先用SolidWorks画出颗粒的三维模型,再将画好的模型导入到EDEM的颗粒工厂中。由于肥料的含水率小于0.5%,颗粒表面几乎没有粘附力,颗粒间没有复杂的相互作用力。所以,此次仿真时颗粒的接触模型为Hertz-Mindlin模型。由于颗粒的大小不一,参照图2(a)中三轴尺寸概率分布,建立颗粒工厂时,设置颗粒大小在其均值0.7～1.2倍之间随机生成。为了减少仿真时间、加快仿真速度,在颗粒生成时设置颗粒以2m/s的初始速度下落。

图4 钾肥颗粒模型Fig.4 Model of potash fertilizer

1.3.2 仿真试验设计

仿真试验时,将8个试验变量分为高、低两个水平进行Plackett-Burman试验设计,高水平编码为1,低水平编码为-1。试验采用1个中心点,共进行13次仿真试验。试验因素水平如表2所示。

进行仿真时采用的圆筒内径为98mm、高为220mm,底板是长为400mm的正方形板,无底圆筒和底板的材料均为钢板。颗粒工厂建在距离底板为150mm的圆筒内,其内径为98mm。仿真开始前,无底圆筒和底板紧密接触;仿真开始时,颗粒从颗粒工厂生成并以2m/s的初始速度往下落,等到所生成的颗粒占圆筒体积2/3时,颗粒工厂停止生成颗粒;颗粒在圆筒内稳定时,圆筒以0.05m/s的速度匀速上升,直到所有的颗粒都离开圆筒并堆积到底板上并达到稳定状态时,测量颗粒的休止角,如图5所示。

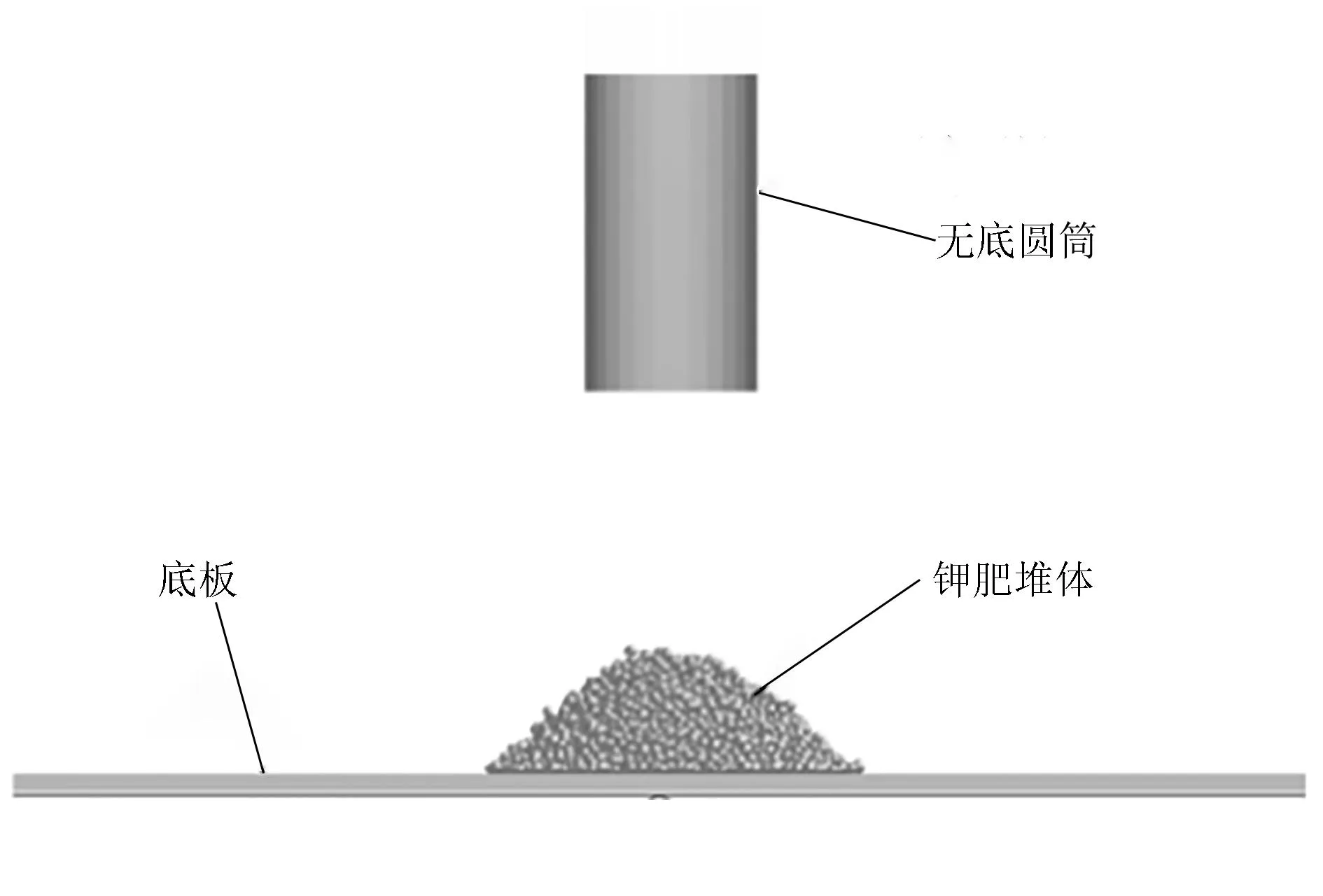
图5 休止角仿真Fig.5 Angle of repose simulation

2 仿真结果与分析

2.1 显著参数的确定

根据Plackett-Burman试验方案,用EDEM软件进行仿真,仿真结束后利用EDEM软件量角器模块测出每组试验的休止角,通过Plackett-Burman试验筛选出对休止角具有显著影响的参数。Plackett-Burman试验方案及试验参数显著性分析分别如表3、表4所示。

表3 Plackett-Burman试验方案Table 3 Scheme of Plackett-Burman experiment

续表3

表4 Plackett-Burman试验参数显著性分析Table 4 Analysis of significance of parametersin Plackett-Burman test

分析表4可知:钾肥-钾肥静摩擦因数(X5)及钾肥-钾肥滚动摩擦因数(X7)对肥料休止角具有显著的影响(P<0.05),其他参数的显著性水平远大于0.05,表明其他因素对颗粒休止角的影响不明显。因此,只需要对X5及X7这两参数进行最陡爬坡试验及Box-Behnken试验。

在进行最陡爬坡试验时,除了显著性参数,其余参数全部取中值,试验设计及结果如表5所示。分析表5可知,由于钾肥-钾肥静摩擦因数、钾肥-钾肥滚动摩擦系数对休止角的效应均为正值,所以随着这两个参数的变大,休止角也在变大;在3号爬坡试验时,相对误差最小。所以,取3号试验为中心点,2号、4号分别为低水平、高水平进行Box-Behnken试验。

表5 最陡爬坡试验设计及结果Table 5 Design and results of steepest ascent test

2.2 显著参数的响应面优化

在进一步确定显著性参数的取值范围后,其余显著性较小的参数全部取中值进行试验,对显著性参数进行Box-Behnken试验,设计3个中心点,共进行15次试验,得到的结果如表6所示。

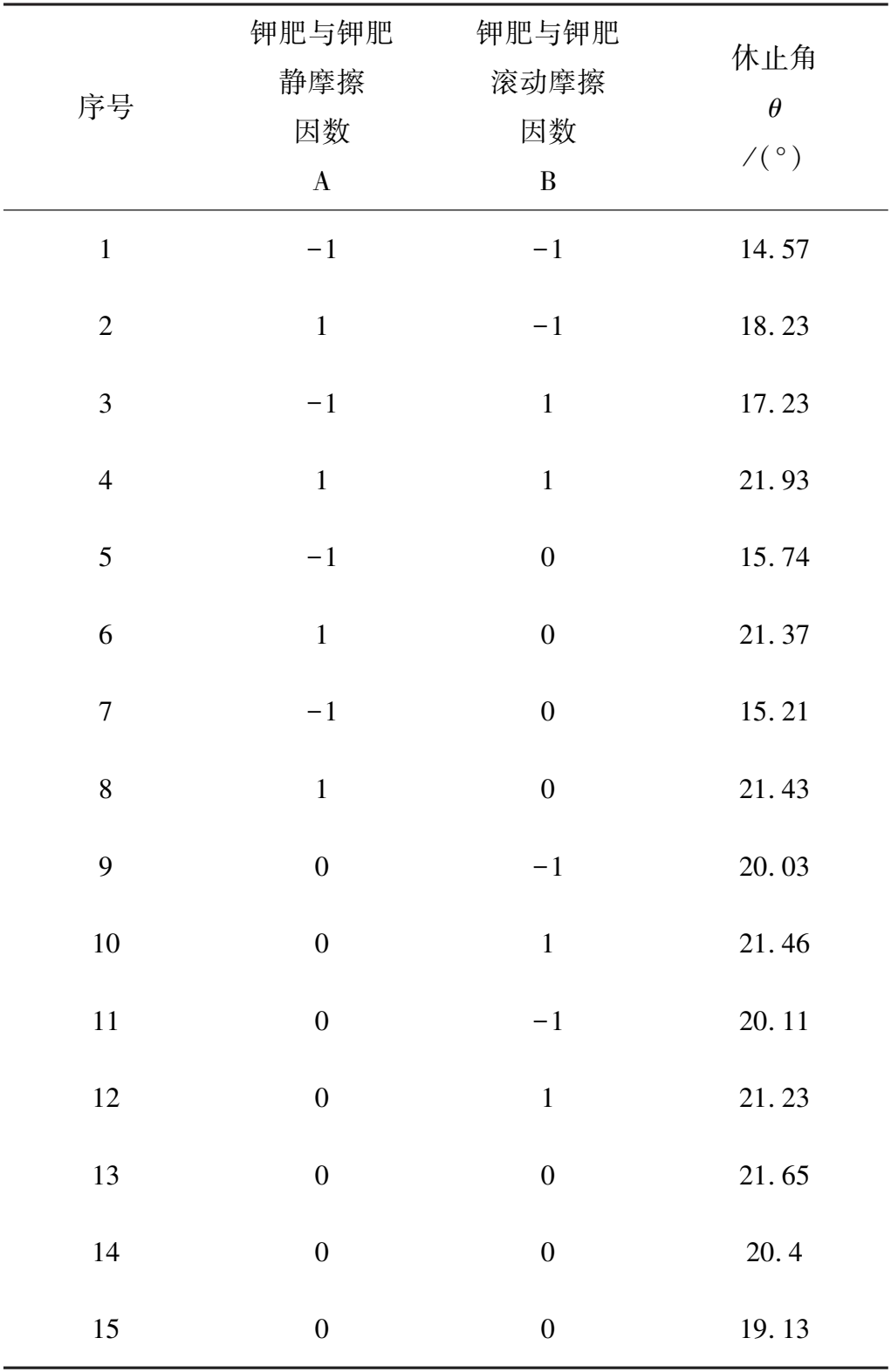
表6 Box-Behnken试验设计及结果Table 6 Design and results of Box-Behnken test

根据表6的仿真结果,用Design-Expert软件对该结果进行二阶回归建模,二次多项式模型方差分析(见表7),得到其二次多项式的方程为

θ=-4.16+97.50A+8.04B+17.33AB- 105.15A2-9.60B2

(1)

表7 Box-Beknken实验设计二次多项式模型方差分析Table 7 ANOVA of quadratic polynomial model of Box-Behnken test

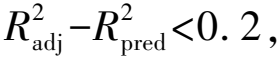
为了得到模拟度更好的方程,去除显著性不高的项,即去除AB项及B2项,对该模型进行优化,优化后的回归模型方差分析如表8所示。优化后的二阶回归方程为

θ=-0.016+166.90A+6.75B-356.11A2

(2)

表8 Box-Behnken试验优化模型方差分析Table 8 ANOVA of modified model of Box-Behnken test

续表8

由表8可看出:优化后变异系数CV由4.64%降至4.28%;失拟项由0.1757增至0.3162,说明模型比优化前更加合理;精密度也由12.85上升到17.046,这表明该模型具有较高的精准度,可以用来预测肥料的休止角。

应用Design-Expert绘制钾肥-钾肥静摩擦因数和钾肥-钾肥滚动摩擦因数的响应曲面图,如图6所示。由图6可直观看出:当钾肥-钾肥静摩擦因数为0.4、钾肥-钾肥滚动摩擦因数为0.2时,仿真休止角为21.65°;对比图3休止角堆积物理试验结果21.64°,其相对误差为0.046%,即其他非显著性参数选中值时,钾肥-钾肥静摩擦因数取0.4,钾肥-钾肥滚动摩擦因数取0.2时相对误差最小。

图6 钾肥-钾肥静摩擦因数和钾肥-钾肥滚动摩擦因数响应曲面Fig.6 Response surface diagram of potash fertilizer- potash fertilizer static friction coefficient and potash fertilizer- potash fertilizer rolling friction coefficient

3 验证试验

将仿真试验休止角与堆积试验休止角进行对比,如图7所示。通过最陡爬坡试验及二阶回归模型参数优化之后,确定了钾肥-钾肥静摩擦因数为0.4,钾肥-钾肥滚动摩擦因数为0.2,其余非显著性参数取中值时(钾肥泊松比为0.25、钾肥剪切模量为7.3×107、钾肥-钾肥恢复系数为0.35、钾肥-钢板恢复系数为0.25、钾肥-钢板静摩擦因数为0.3、钾肥-钢板滚动摩擦因数为0.245),休止角的相对误差最小。为验证最优参数的准确性,采用上述参数重复进行5次仿真,仿真休止角分别为21.65°、21.45°、21.08°、20.4°、21.08°,真实休止角为21.64°。用T检验法得t=1.425

(a) 仿真试验休止角

(b) 堆积试验休止角图7 仿真休止角与真实休止角对比验证Fig.7 Comparison between simulated repose angle and real repose angle

4 结论

1)测量了钾肥的三轴尺寸、质量及密度,并通过查阅相关文献,确定了其它离散元参数的取值范围。

2)在确定离散元参数的取值范围的前提下,用Plackett-Burman筛选出了对休止角影响显著的参数(钾肥-钾肥静摩擦因数、钾肥-钾肥滚动摩擦因数),并通过最陡爬坡试验进一步缩小了显著性参数的取值范围。

3)在缩小显著性参数的取值范围后,通过Box-Behnken试验建立并优化了显著性参数的二阶回归方程,结果表明:当钾肥-钾肥静摩擦因数为0.4、钾肥-钾肥滚动摩擦因数为0.2,其余参数取中值(钾肥泊松比为0.25、钾肥剪切模量为7.3×107、钾肥-钾肥恢复系数为0.35、钾肥-钢板恢复系数为0.25、钾肥-钢板静摩擦因数为0.3、钾肥-钢板滚动摩擦因数为0.245)时,仿真休止角与真实休止角的相对误差为0.046%,并通过T检验法验证了真实休止角与仿真休止角的值无显著差异。