梁端水平折角对城市轨道交通专用桥行车性能的影响

刘科宏, 向活跃

(西南交通大学, 四川成都 610031)

0 引言

随着城镇化的不断推进,城市轨道交通得到了快速的发展[1]。轨道交通桥梁跨度不断增大。在风、车辆荷载等作用下,桥梁会发生水平变形,在梁端产生水平折角[2]。梁端水平折角一方面会使车辆对轨道产生较大的冲击作用,对轨道耐久性和稳定性非常不利[3],另一方面过急过大的梁端水平折角会导致列车横向响应增加,影响列车的安全性和舒适性。由于城市轨道交通专用桥梁宽度较小,当桥梁跨径增大时,横向刚度会成为限制跨度增加的主要因素之一[4-5]。横向刚度可通过横向挠跨比、梁端水平折角等指标进行评价,横向挠跨比用于控制列车要桥上的行车安全性和舒适性。而对于梁端的行车安全性和舒适性采用梁端转角更为合适。

陶兴等[6]收集了各国轮轨规范中的横向刚度限值与制定思路,提出中低速磁浮轨道梁横向刚度限值建议值。王其昌等[7]利用翟婉明教授所确立的车辆-轨道耦合动力学理论与方法,对路桥过渡段进行了动力学性能计算与评价,并给出了高速铁路路桥过渡段轨道折角的容许值。柯在田等[8]通过对国外规范标准和研究进行对比分析,结合我国铁路提速的桥梁动载试验数据,提出由墩台横向水平位移差引起的相邻结构物轴线间的水平折角不得超过1(rad/1000)。王贵春[9]以轨道折角作为不平顺激振源,分析了轨道水平折角对车辆走行性的影响。阚正明等[10]与王晓昱[11]研究了在横向地震作用下,桥墩刚度、扣件横向刚度对梁缝处轨道折角的影响,并结合相关规范对轨道变形的安全性进行了评价。刘安全等[12]对在役大跨度悬索桥刚度设置和运营状态进行广泛调研与总结,提出了大跨度轨道悬索桥水平折角限值。

对于中小跨度城市轨道交通专用桥梁,由于本身横向刚度非常大,在设计阶段往往满足横向刚度的要求,产生的水平位移和梁端水平折角非常小,此时梁端水平折角对车辆走形性影响有限[13]。对于大跨度城市轨道交通专用桥梁,结构自身的柔性及车辆荷载和风载的作用会进一步加大桥梁的梁端水平折角,桥梁曲线变化和梁端水平折角常常是设计的控制性因素[14]。已建大跨度轨道交通专用桥梁的运营实践表明,桥梁在列车通过时,出现明显晃动的现象,列车在进桥和出桥时乘客经常会感受到明显的车体振动[15],此时的舒适性相对较低。因此,针对大跨度城市轨道交通专用桥梁端水平折角的影响开展研究显得尤为必要。

本文四座城市轨道交通专用桥为背景,将主梁在横风作用下的主梁变形得到不同梁端水平折角,与横向轨道不平顺叠加进行车-桥耦合振动分析,讨论了梁端水平折角对车辆走行性的影响,并将结果与现行规范进行了对比。

1 分析模型

1.1 车-桥耦合振动模型

车辆动力学模型中通常将车辆各个部件视作为刚体[16],刚体之间通过阻尼或弹性元件相互连接。整体车辆可采用质点-弹簧-阻尼器模型,车辆模型如图1所示。车辆模型更多细节可参考文献[15]。

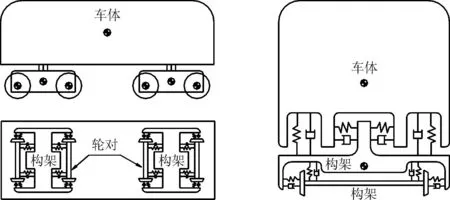
图1 车辆分析模型

选取四座城市轨道交通专用桥[17]作为背景研究,这四座大桥不仅跨度区别明显并且桥型不同。其中大桥的结构布置图如图2所示。桥型和主跨信息见表1,桥梁结构模型采用有限元方法建立杆系模型,主梁和桥塔均采用空间梁单元模拟,大缆和斜拉索采用空间杆单元模拟。

表1 桥梁信息

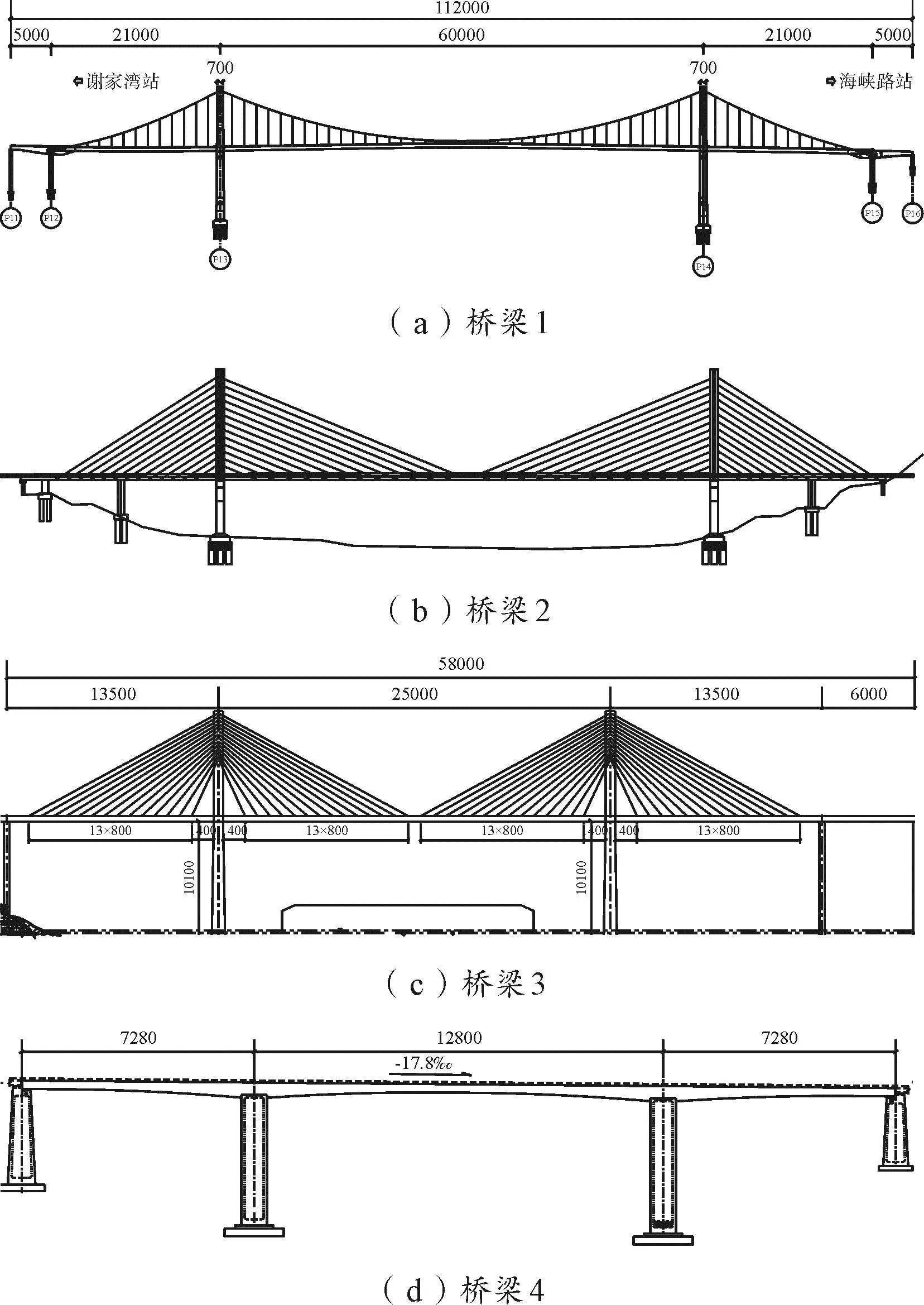
图2 桥梁总体布置(单位:cm)

通过轮轨间的几何位移关系及力学关系实现车辆和桥梁两子系统间的耦合,则车-桥系统的运动方程为式(1)、式(2)[18]。

(1)

(2)

式中:M,C,K分别为质量、阻尼、刚度矩阵;下标b,v分别表示桥梁及车辆;Fvb,Fbv分别表示车-桥系统间的相互作用力。

仅考虑入桥侧的梁端水平折角作用,轨道不平顺采用美国5级谱进行模拟[19],列车模型采用城市地铁B型车,分析中车速取为80 km/h,空间步长取为0.2 m。

1.2 水平折角的实现

大跨度桥梁约束形式复杂,梁端水平折角与主桥的变形和墩顶位移有较大关系,通常引桥和主桥共用一个桥墩,两者的道路形成一个连续整体。为了模拟梁端水平折角,主桥的边墩处设置了横向简支段,主桥的变形造成墩顶水平位移,以此带动简支段引桥进行刚体位移,两者在梁端处的夹角即为梁端水平折角[20](图3)。

图3 梁端折角示意

通常而言,轮轴横向力、船舶撞力和风荷载会导致梁端水平折角,但轮轴横向力相对较小,船舶撞击力较大,但边墩通常未在主航道上,发生船撞的概率相对较小。因此,通过对主桥施加风荷载,在梁端产生一定的主桥水平转角和墩顶水平位移以形成梁端水平折角。将桥梁水平方向的位移与轨道横向不平顺叠加,作为新的轨道不平顺进行分析。换而言之,梁端折角以轨道不平顺的形式影响车桥响应,具体表现在施加额外桥梁变形。

通过改变风速得到的梁端水平变形图如图4～图6所示。考虑了16 m、32 m、56 m 3种简支段引桥跨径。在此仅列出桥梁一与桥梁三的梁端水平变形图。图4与图6中不同简支段跨径组合示意图对应风速为25 m/s,图5中引桥简支段跨径取为32 m。

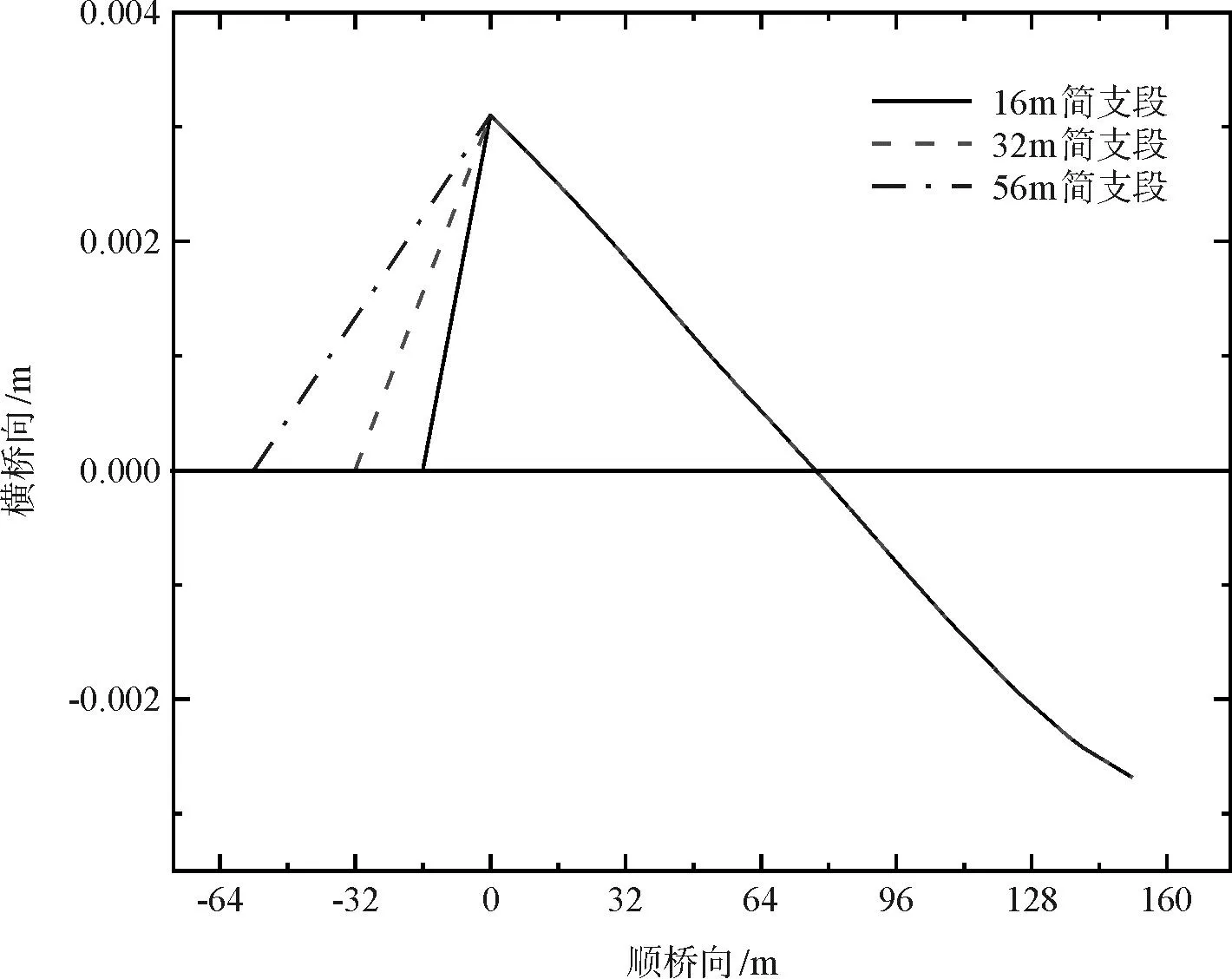
图4 不同跨径组合下的梁端变形(桥梁一)

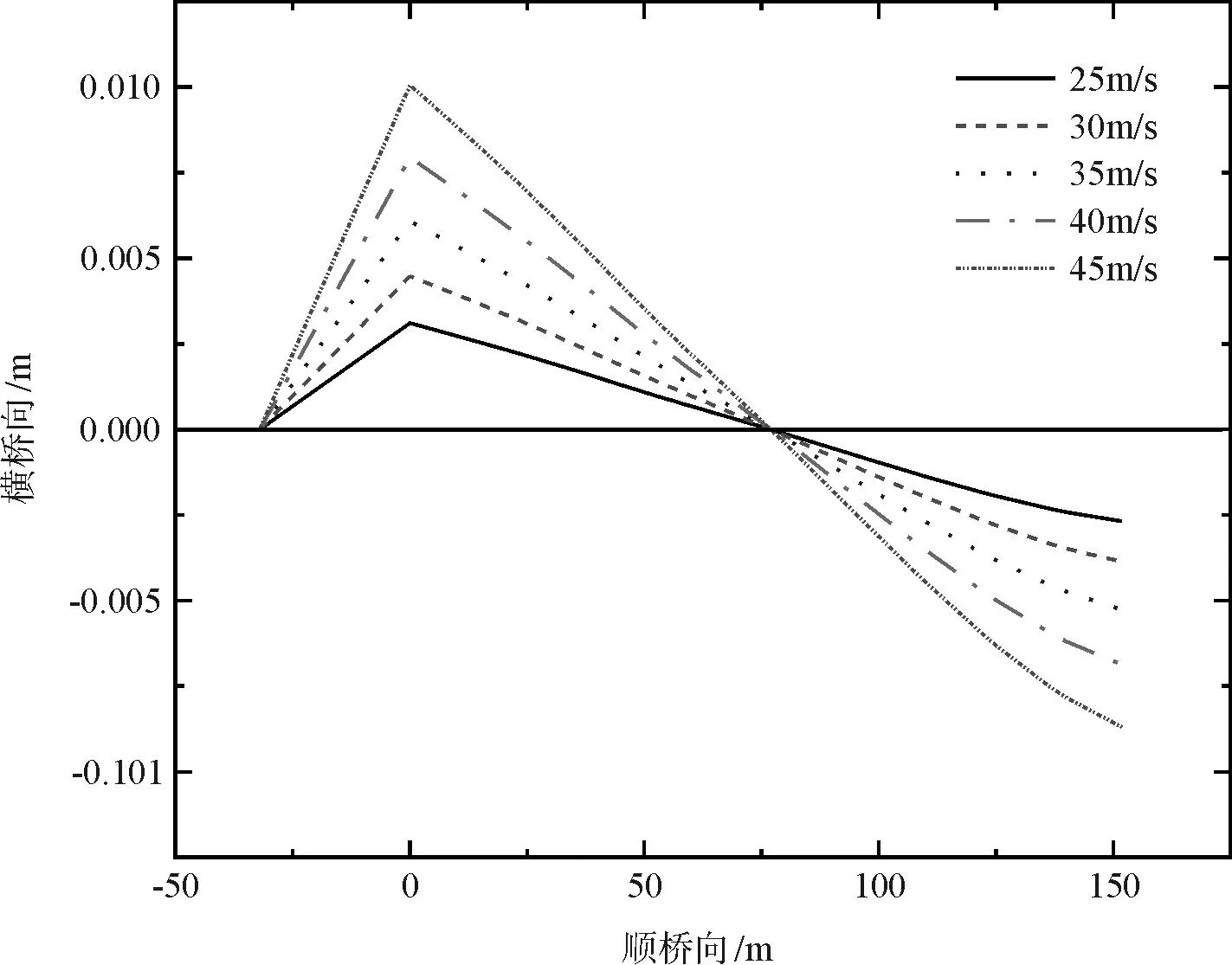
图5 不同风速下的梁端变形(桥梁一)

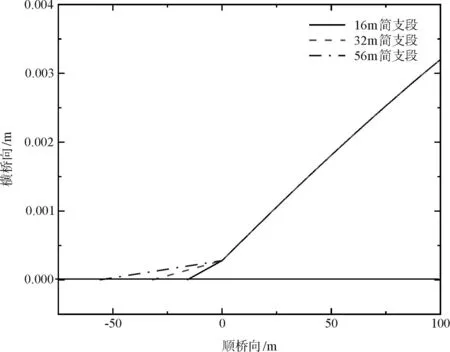
图6 不同跨径组合下的梁端变形(桥梁三)

从图5可见,因简支段引桥跨径相较于墩顶水平位移大的多,梁端水平折角总体上会随着风速的增大而增大。简支段引桥跨径的影响会因主桥变形形态不同而改变。对于桥梁一(图4、图5),梁端水平折角会随着简支端跨度的增大而减小。对于桥梁三(图6),理论上调整简支段跨径至梁端处主桥与引桥节段在一条直线上时,梁端水平折角为0,当跨径改变偏离时,梁端水平折角增大。

简支段的存在使得主桥线形得以平稳过渡。另一方面,其与主桥的相对变形是水平折角形成的直接原因。所以设计时有必要将梁端水平折角同引桥简支段结合在一起研究其对车辆响应的影响。由于桥梁水平变形与横向不平顺的叠加存在两种方向,即同向与反向。本文考虑了两种叠加方式,并取车辆响应较大者的最不利工况。因此横向不平顺对梁端水平折角也有一定的关系。

2 结果分析

2.1 水平折角的影响

考虑简支段引桥跨径的影响,计算了上述四个桥梁在不同水平折角下的轮重减载率与脱轨系数。设计车速为80 km/h。图7给出16 m简支段引桥跨径时四座桥梁的梁端水平折角与车辆响应关系图。

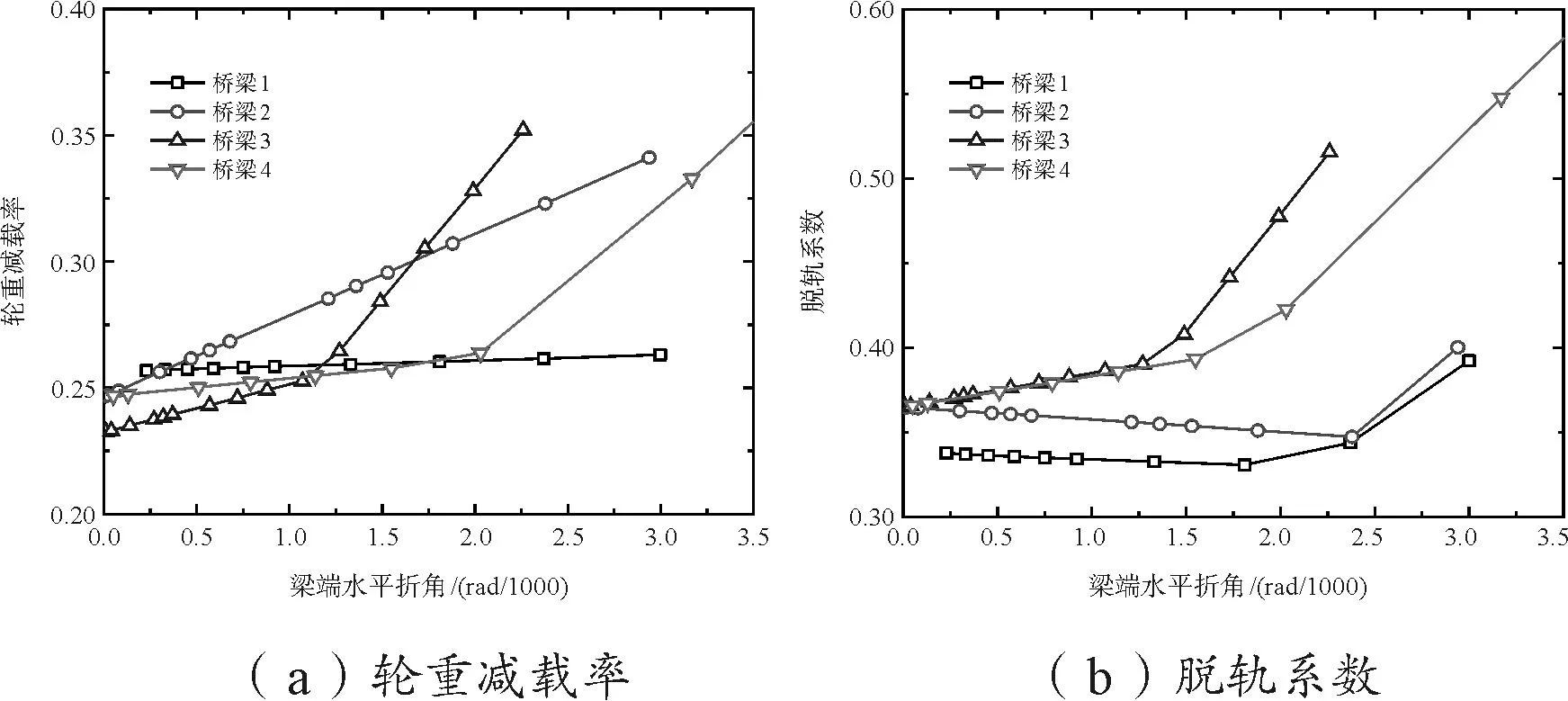
图7 不同桥梁车辆响应

从图7中可以看出随着梁端折角的增大,车辆的轮重减载率和脱轨系数总体上呈增大趋势,且在部分工况中这种增大趋势在水平折角偏大时存在明显的突变陡增。为了叙述的方便,后续将突变处所对应的梁端水平折角称为敏感梁端水平折角。

在敏感梁端水平折角两侧,车辆响应近似以线性变化,不同桥梁的敏感梁端水平折角差异较大。从图7(b)可见,当水平偏角小于敏感梁端水平折角时,桥梁一与桥梁二的脱轨系数呈减小趋势。考虑到水平偏角的增大代表着更大的桥梁额外变形,可以知道当水平偏角小于敏感梁端水平折角时,桥梁受到的外部激励以固定的横向轨道不平顺为主,水平偏角相较而言仅略微增加甚至削弱轨道不平顺的影响,车辆响应变化较为缓慢;而当水平偏角大于敏感梁端水平折角时,水平偏角作为外部激励占主导地位,车辆响应随偏角变化率加大。

2.2 引桥跨径的影响的影响

图8给出16 m、32 m、56 m简支段引桥跨径时四座桥梁的梁端水平折角与车辆响应关系图,因变化规律接近,仅展示脱轨系数图。

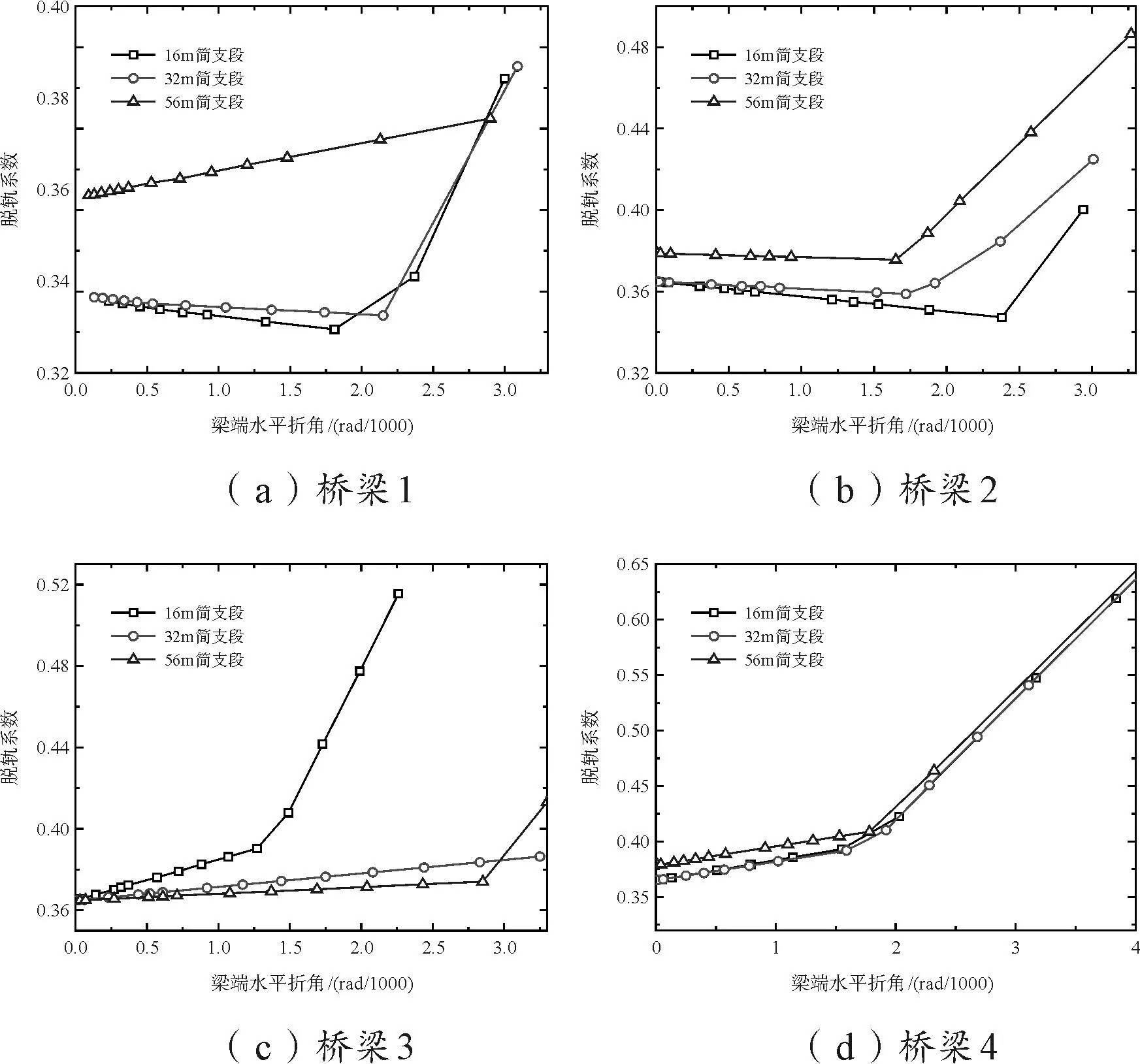
图8 不同简支段引桥跨径脱轨系数

本文导入的不平顺信息包括轨道不平顺与不平顺差分,代表简支段引桥、主桥的额外变形与变形偏角。从图8可以看到,当水平折角较小时(接近0),简支段跨径越小,车辆响应越小。这是由于此时简支段引桥与主桥额外变形较小,车辆响应差异被简支段引桥刚度主导。

随着水平折角的增大,必须考虑主桥的额外变形形态与墩顶位移引起的简支段额外变形对车辆响应差异的影响。鉴于桥梁一的额外变形皆满足线性变化(图4、图5),为了分析的便捷性,首先研究其响应变化规律。

从图8(a)可见,随着简支段跨径的增大,敏感梁端水平折角也在增大,当梁端水平折角较大时,简支段引桥跨径越大,车辆响应越小,响应变化速度越小。由2.2节可知,当水平折角相同时,随着简支段跨径增大,墩顶水平位移增大(模拟时施加的风速增大),主桥额外变形与变形偏角增大,简支段最大额外变形增大,变形偏角减小。结合车辆响应结果,可以知道当水平折角较大时,水平折角主要通过简支段偏角主导车辆响应,敏感梁端水平折角是简支段偏角成为影响车辆响应的主要因素的结果。

这种由于简支段变形偏角差异导致的简支段跨径不同时车辆响应变化差异(简称为偏角效应)会受到主桥的刚度分配的影响。首先考虑主桥梁体横向刚度较小而相较而言下部结构横向刚度较大的情况(尤见于斜拉桥等柔性桥型),研究桥梁二与桥梁三的额外变形形态。当水平折角较大时,两者简支段变形偏角均大于主桥梁端的变形偏角,水平折角随墩顶位移的增大而增大。因此当水平折角相同时,随着简支段跨径增大,墩顶位移减小,主桥额外变形与变形偏角减小,简支段最大额外变形减小,变形偏角减小。根据车辆响应结果可知(见图8(b)与图8(c)),桥梁三因为主桥额外变形的原因表现出更明显的偏角效应,但桥梁二的偏角效应则不明显。分析变形可知,相较于桥梁三,桥梁二下部结构横向刚度比主桥梁体横向刚度大的多,这导致桥梁二主桥梁端偏角关于墩顶水平位移的变化率比桥梁三大,这减小了简支段跨径不同导致的墩顶水平位移与简支段变形偏角的差异,缓解了偏角效应。

现在讨论主桥梁体横向刚度较大而相较而言下部结构横向刚度较小的情况(尤见于连续刚构桥)对于桥梁四,当水平折角较大时,简支段变形偏角小于主桥梁端的变形偏角,水平折角随墩顶位移的增大而增大。因此当水平折角相同时,随着简支段跨径增大,墩顶位移增大,主桥额外变形与变形偏角增大,简支段最大额外变形增大。简支段跨径不同导致简支段变形偏角差异相较于桥梁四更小,甚至当主桥横向刚度与下部结构横向刚度比值较小时,会出现反向的偏角效应。桥梁四的车辆响应结果验证了这一理论。

总结可知,简支段引桥跨径对车辆响应的影响需要结合桥梁变形进行考虑。一般而言,使用跨径较大的简支段引桥往往代表更大的敏感梁端水平折角,即车辆响应随水平折角变化更平滑,但需要考虑低水平折角情况下简支段刚度的影响。若简支段跨径较小,对于悬索桥与斜拉桥等柔性桥型,建议使用刚墩柔梁的设计策略;或者将桥设计为连续刚构桥。

2.3 规范对比

根据计算结果,当梁端折角大于1.00 (rad/1000)时,部分工况梁端折角造成的车辆响应会有明显的增大,但在0～2.0 (rad/1000)的水平折角范围内,车辆的安全参数响应都小于GB/T 51234-2017《城市轨道交通桥梁设计规范》中脱轨系数0.8,轮重减载率0.6的限值,且有较大的安全储备。GB/T 51234-2017《城市轨道交通桥梁设计规范》中对于墩顶横向位移限值为4L^0.5,该标准总体上与水平折角1.50 (rad/1000)对应,因此建议大跨度城市轨道交通桥梁的梁端水平折角仍采用现行规范的值进行控制。

3 结束语

本文选取四座城市轨道交通桥梁作为工程背景,通过将桥梁在横风作用下的横向变形同轨道不平顺进行叠加,进行车-桥耦合振动分析,讨论了梁端水平折角对车辆走行性的影响,研究结论:

(1)简支段引桥的存在使得主梁线形得以平稳过渡,也影响了水平折角的形成。这一效应需视主梁水平变形和桥型而定。

(2)车辆响应随水平折角的变化总体上呈分段近似线性递增的趋势。当水平偏角偏小时,车辆响应主要受随机轨道不平顺影响,变化相对较小。当水平偏角偏大时,水平折角的影响占主要作用。

(3)水平折角主要通过简支段引桥偏角影响车辆响应。水平折角较小时,简支段引桥跨径越小,响应越小。水平折角较大时,不同主桥下列车响应随简支段引桥跨度的变化规律有所差异。

(4)建议大跨度城市轨道交通桥梁梁端水平折角仍采用现行规范的值进行控制。