结合遗传算法和滚动调度的多机器人任务分配算法

邓辅秦，黄焕钊，谭朝恩，付兰慧，张建民，林天麟

结合遗传算法和滚动调度的多机器人任务分配算法

邓辅秦1，2，黄焕钊1，谭朝恩1，付兰慧1，张建民1，林天麟2*

（1.五邑大学 智能制造学部，广东 江门 529020； 2.香港中文大学（深圳）深圳市人工智能与机器人研究院，广东 深圳 518116）（∗通信作者电子邮箱tllam@cuhk.edu.cn）

研究多机器人任务分配（MRTA）的目的是提高智能工厂中机器人完成任务的效率。针对现有算法在处理大规模、多约束的MRTA时存在不足的问题，提出一种结合遗传算法和滚动调度的MRTA算法（ACGARS）。首先，在遗传算法中采用基于有向无环图（DAG）的编码方式高效地处理任务之间的优先级约束；其次，在遗传算法的初始种群中加入先验知识以提高算法的搜索效率；最后，设计基于任务组的滚动调度策略用于减小求解问题的规模，从而实现对大规模问题的高效求解。在大规模问题实例上的实验结果表明，相较于构造性启发式算法（CHA）、最小化干扰算法（MIA）和基于惩罚策略的遗传算法（GAPS）生成的方案，当任务组数为20时，所提算法生成的方案的平均订单完成时间分别缩短了30.02%、16.86%和75.65%，验证了所提算法能有效地缩短订单的平均等待时间，提升多机器人任务分配效率。

多机器人任务分配；遗传算法；智能工厂；有向无环图；滚动调度策略

0 引言

随着人们生活水平的不断提高和信息技术的不断发展，个性化的消费形式正逐步取代大范围、单调统一的消费形式。个性化消费基于订单消费的小批量、定制化和多种类等特性，将成为未来主流消费方式，因此按需批量生产个性化产品也是智能制造业未来转型升级的主要发展趋势，而智能工厂是智能制造过程的关键部分［1］。智能工厂需要根据收到的每个订单的个性化需求与所需产品数量灵活安排多个产品的生产流程，从而生产订单需要的产品，快速响应市场需求；但是，传统的工厂固定的生产模式无法满足客户小批量高度定制产品的需求。针对传统工厂的缺点，目前已有许多先进的智能工厂解决方案。其中，基于模块化自重构机器人［2］的多机器人系统是一种具有代表性的制造系统［3-4］。多机器人系统将订单视为一组生产制造任务，并控制多个机器人共同协作完成任务。相较于传统工厂，多机器人系统能够根据不同订单的需求灵活地为每个任务分配不同数量的机器人。这些基于模块化自重构机器人可以根据任务的需求进行重构［5］，满足动态的个性化订单需求。

在智能工厂的多机器人系统中，需要控制数量庞大的机器人，目标是合理规划机器人执行计划，最小化订单的平均等待时间，从而快速响应需求。因此在设计、构建和使用多机器人系统时，需要解决的一个问题是：系统中各个机器人在各个时刻分别应该选取什么动作，执行什么任务？即多机器人任务分配（Multi-Robot Task Allocation， MRTA）问题。MRTA问题存在于许多领域，例如农业生产［6-8］、灾后搜索救援［9-11］、水下监测［12-13］和环境探索［14］等。本文重点研究智能工厂背景下的MRTA问题。在该问题中，机器人每次只能执行一个任务，每个任务需要多个机器人组成团队协同执行。由于任务数较多，机器人需要在不同的时间内完成多个任务；此外，任务之间存在优先级关系，所以机器人执行任务的情况不仅与自身有关，还会受到其他机器人的影响［15］，使得高质量调度方案的生成较难。根据文献［16］，该MRTA问题在iTax分类法下属于单任务机器人、多机器人任务和包含跨时间表依赖的时间扩展分配类型的MRTA问题。

目前，已有许多类型的方法用于解决MRTA问题，包括精确算法［14，17］、基于机器学习的方法［18］、基于规则的启发式算法［19］和遗传算法［20-25］等。面对这一类MRTA问题，精确算法虽然能得到最优解，但它的求解时间随着问题规模的增加呈指数增长［26］；而基于机器学习的方法则需要花费大量成本用于制作训练集［18］。目前求解这一类MRTA问题的主要方法是基于规则的启发式算法和遗传算法：基于规则的启发式算法按照一定的规则将任务分配给相应的机器人团队，简单易实现，但算法并不以全局最优为目标，且在不同的案例中性能可能会有很大的差异；而遗传算法则是将任务分配方案编码为个体，用适应度函数评价个体的竞争力，然后模仿自然进化的方式搜索最优个体。近年来，许多研究团队使用遗传算法解决MRTA问题［21-25］：文献［24］中提出一种多种群遗传算法用于求解多无人水下航行器的任务分配问题；文献［25］中为仓储物流应用中的多机器人系统设计了基于遗传算法的任务分配方法。针对任务之间的优先级约束，在Miloradović等［21-22］提出的遗传算法中，设计了优先约束修复算子用于修复违背约束的个体，确保生成的个体都能够满足优先级约束。虽然进化算法在MRTA问题的应用研究广泛，但大多数研究的问题集中于单机器人任务类型，即每个任务只需要一个机器人执行，没有同时考虑多机器人协作与有任务优先级，与本文研究的问题属于不同类型。当前用于解决这类MRTA问题的主要方法是基于惩罚策略的遗传算法（Genetic Algorithm with Penalty Strategy， GAPS）［20］。GAPS根据生成解方案的违背约束程度，在相应个体的适应度函数上增加惩罚函数，在处理小规模问题时简单高效；然而在面对较大规模问题时，由于任务之间优先级关系数量与复杂性增加，导致生成的个体更容易违背约束，使算法的寻优能力下降。

综上所述，虽然现有用于求解MRTA问题的遗传算法较多，但都不能较好地解决大规模的包含任务优先级约束的MRTA问题。针对这个问题，本文提出了一种结合遗传算法和滚动调度的MRTA算法（MRTA Algorithm Combining Genetic Algorithm and Rolling Scheduling， ACGARS）。本文算法主要有以下特点：首先，针对GAPS搜索能力不足的问题，增强算法处理优先级约束的能力，本文提出使用拓扑图的编码方式的遗传算法，使算法能够处理任务之间的优先级约束，使算法在搜索的过程中不会产生不可行解，并在初始化种群时加入先验知识，引导算法的优化，通过这两种方式提高算法搜索能力；其次，针对算法在处理更大规模问题时搜索效率下降的问题，采用基于滚动调度的策略，对问题进行分解以减小求解问题的规模，并增强算法对动态环境的反应能力。

1 问题描述

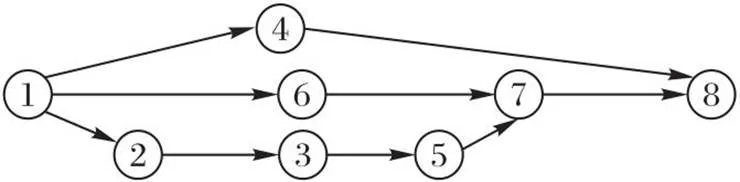
图1　代表一个任务组的DAG

问题的方案包括每个机器人执行任务的顺序以及任务的起始时间与结束时间，通过这两部分确定每个机器人执行任务的时间表。为了得到满足上述约束的解决方案，本文采用混合整数线性规划建立了该问题的全局优化模型描述，式（1）～（12）为该问题的混合整数规划（Mixed-Integer Linear Programming， MILP）模型：

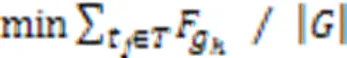
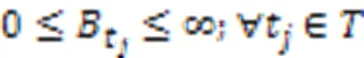
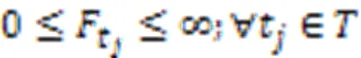
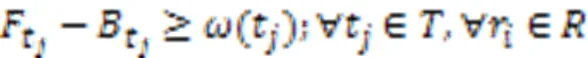
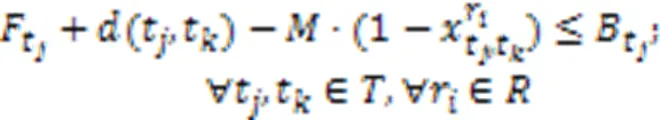
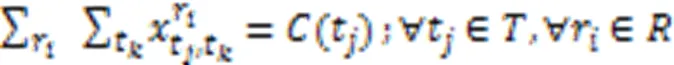
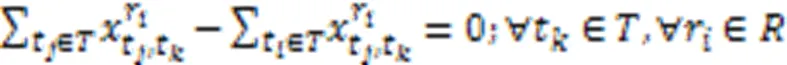
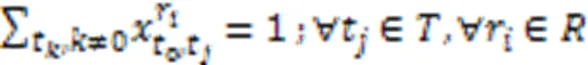
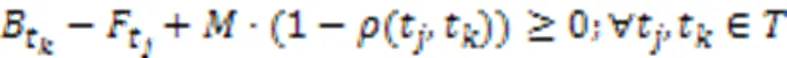
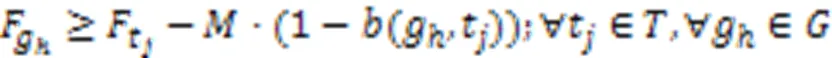
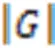
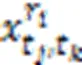
问题的主要特点是需要在多个机器人协作的任务中考虑任务的优先级约束；主要难点是当问题的规模增大时，在合理的时间内得到更高质量的解。

2 本文算法

求解上述问题具有一定的挑战性，因为当问题规模增大时，更多的变量和线性约束使上述模型变得更加复杂［20，27］。面对这类复杂的问题，遗传算法能够在合理的时间内得到高质量的解。因此本文提出一种用于MRTA的算法ACGARS。本文算法的整体框架如图2所示。整个算法主要有两个部分：一部分是改进遗传算法，包括使用基于DAG的编码方式和在初始化种群中加入先验知识，从而使算法能更直接高效地处理优先级约束并提高算法的搜索能力；另一部分则是优化问题的求解方式，采用基于滚动调度策略的方式，利用基于分解的思想将大规模的问题分解为一系列任务组窗口问题，再使用遗传算法进行多次求解，而非直接对整个问题使用遗传算法进行求解，从而减小求解问题的规模，提高算法的求解效率。

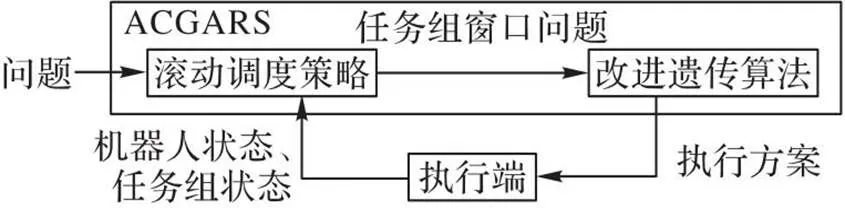
图2　本文算法的整体框架

2.1　改进遗传算法

改进遗传算法的流程如图3所示。首先使用基于优先无环图的编码方式生成初始种群；其次使用基于规则的启发式算法生成的方案作为先验知识，并将这些方案编码为个体加入初始种群；再次算法为种群内的每个个体计算适应度函数，并使用选择算子根据适应度选择用于生成子代的个体；继次通过使用变异算子对选取的个体进行操作的方式生成新一代种群的个体；最后根据是否满足终止条件决定是继续循环生成下一代个体，或是终止循环并输出当前种群中最优个体对应的方案。

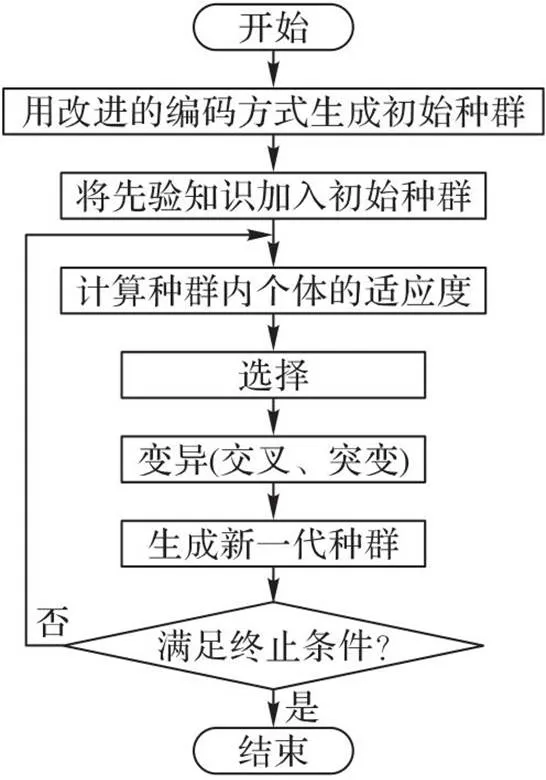
图3　改进遗传算法的流程

2.1.1编码方式

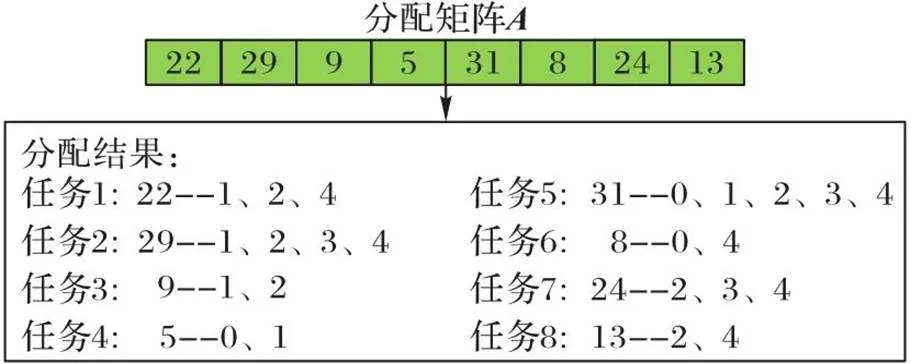
图4　分配矩阵确定执行任务的机器人团队示例

最终的优化目标是最小化所有任务组的平均完成时间。因此，设置适应度函数为每个染色体所对应解的目标函数。因为在搜索过程中不会生成不可行解，所以不需要在适应度函数中设置惩罚项函数。

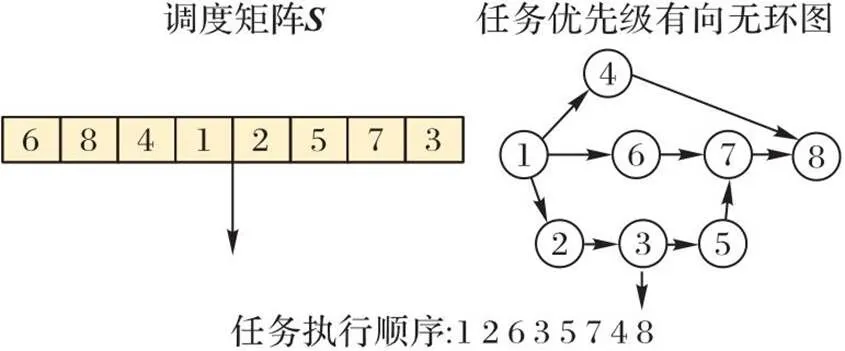
图5　根据DAG与调度矩阵确定任务的执行顺序示例

2.1.2种群初始化

在生成初始种群的过程中，为了提高算法效率，算法使用启发式算法产生的解作为先验知识加入初始种群。具体的实现方式为：首先不同的启发式算法生成对应的解，再将这些解编码成染色体，最后将这些染色体加入初始化的种群。算法选用文献［19，28］中的启发式算法作为先验知识，同时作为后续实验的对比算法。

2.1.3操作算子

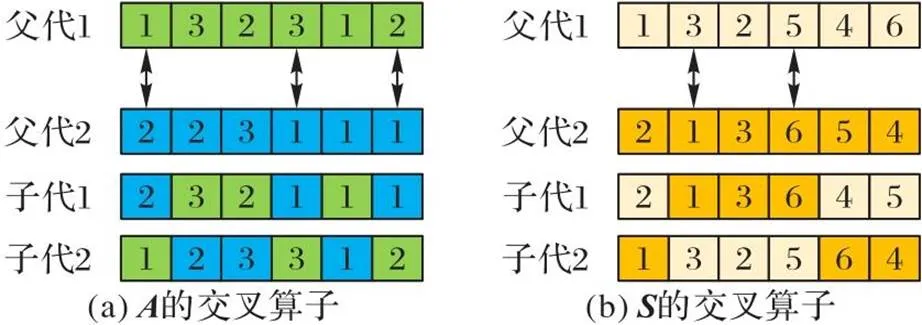
图6　交叉算子示意图

图7　突变算子示意图

通过上述的操作算子可以生成子代种群，然后在父代种群中，选取最好的个体直接复制到子代种群中，并替换最差的个体。这种精英保留策略能够让遗传算法更快地收敛。

2.2　基于任务组窗口的滚动调度策略

虽然改良后的遗传算法在搜索效率上有了较大的提高，但是随着机器人与任务组数增加，问题规模也在增大。为了高效地求解大规模的问题，本文借鉴了文献［29］中的思想设计了基于任务组窗口的滚动调度策略，将大规模的问题分解为一系列小规模的子问题。滚动调度策略流程如图8所示。

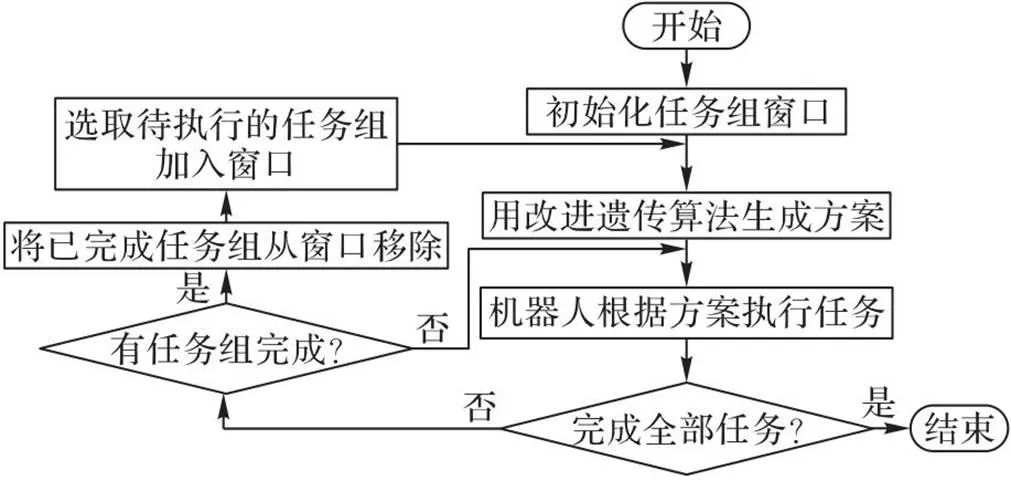
图8　基于任务组窗口的滚动调度策略的流程

首先，算法根据任务组的工作量选取一定数量的任务组（选取的任务组集合即为任务组窗口）；其次，采用改进的遗传算法为任务组窗口内的任务生成调度方案；最后，机器人根据调度方案执行任务。在机器人执行任务的过程中，如果有一个任务组的所有任务都被完成，则将该任务组从窗口中移除，再选取一个未被执行的任务组加入任务组窗口，并再次调用遗传算法重新为窗口内的所有任务生成调度方案。这个过程需重复进行，直到将所有任务组完成。基于这种策略，每次遗传算法只需为一部分任务组而非问题内的所有任务组生成调度方案，虽然牺牲了全局最优性，但减小了遗传算法所需要求解的问题规模，提高了算法的求解效率和对动态环境的适应性，增强了算法的实用性。

3 实验与结果分析

3.1　实验设置

为了验证本文算法的效果，进行数值仿真实验。所有实验在操作系统为Windows 10，编程语言为Python的环境下进行。为了生成随机的MRTA问题实例，本文使用文献［30］中的方法生成代表任务组的DAG。每个任务组的任务数随机选取，范围为［5，10］。每个任务的总工作负载从［10 000，15 000］的整数中采样。机器人在属于不同任务之间转移的时间为1 000单位时间。

为了验证本文算法的效果，将本文算法与构造性启发式算法（Constructive Heuristic Algorithm， CHA）［19］、最小化干扰算法（MinInterfere Algorithm， MIA）［28］和基于惩罚策略的遗传算法（GAPS）［20］进行比较，其中CHA、MIA为基于规则的启发式算法。出于验证算法各模块效果的目的，本文对使用不同模块的算法进行命名：只使用DAG编码的遗传算法命名为改进遗传算法（Improved Genetic Algorithm， IGA）；使用先验知识与DAG编码的遗传算法则称为带先验知识的改进遗传算法（Improved Genetic Algorithm with Priori Knowledge， IGAPK）。为保证实验公平，所有遗传算法的参数都统一设置为：种群规模为40，迭代次数为200，交叉率为0.7，突变率为0.5。其中，种群规模、交叉率和突变率参照文献［20，31］确定；迭代次数设置为200的依据是在实验中观察到的能够确保两个对比算法稳定收敛的最小值；优化的目标函数值为所有任务组的平均完成时间。

3.2　实验结果与分析

3.2.1基于DAG的编码与先验知识对算法的提升

首先，为了验证基于DAG的编码方式效果，本文将IGA与GAPS求解同一问题实例，并观察两者的求解效果。实例中，机器人数为5，任务组数为1，任务的优先级关系如图1所示。每个任务需要的机器人数从［2，5］中随机选取。图9为两个算法生成方案对应的甘特图，图10为两个算法在迭代过程中最优目标函数的变化情况。

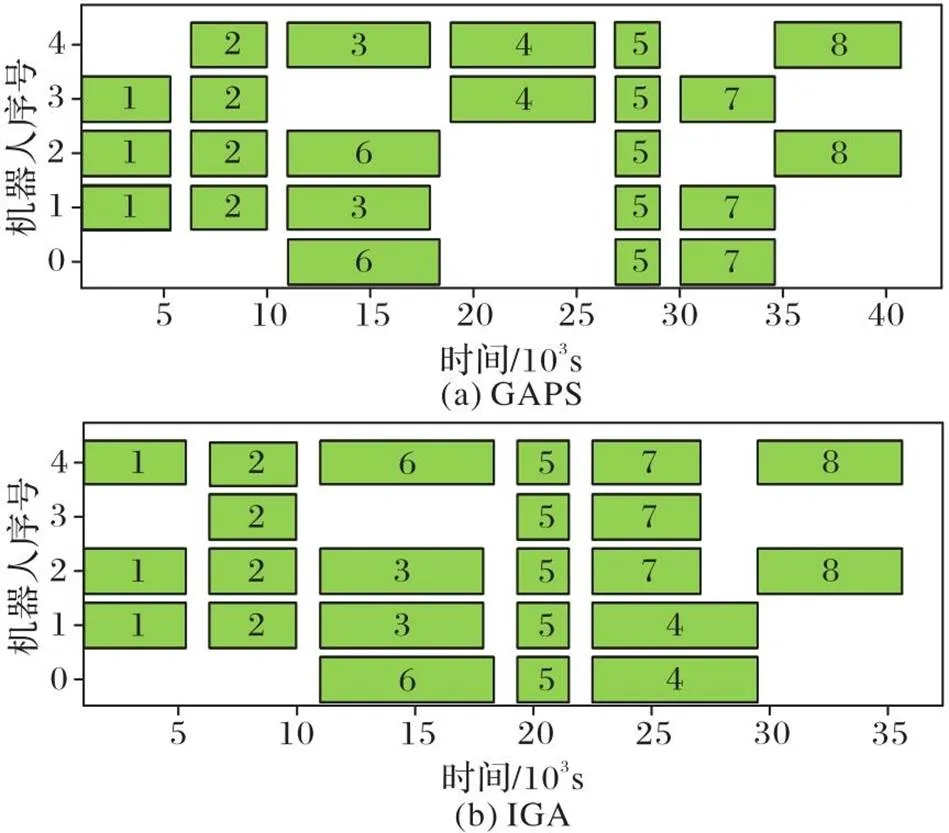
图9　两个算法生成方案对应的甘特图

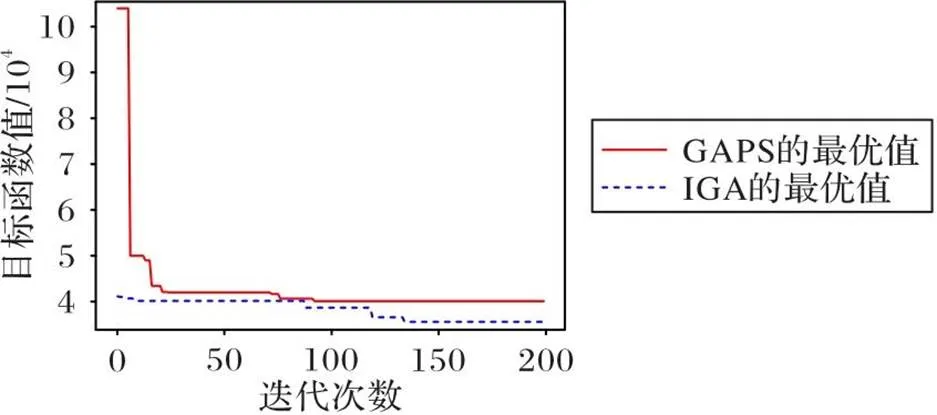
图10　两个算法迭代过程中目标函数最优值的变化

从图9、10中可见，IGA在整个迭代过程中的最优值都优于GAPS，表明使用DAG编码的遗传算法能够更快地得到高质量的求解方案。初始时，IGA的最优值远小于GAPS，这是因为IGA采用基于DAG的编码方式，所以算法的初始种群中的解都满足任务之间的优先级约束；而GAPS算法处理优先级约束的方式是在违背约束的解的适应性函数中增加惩罚函数，它的编码方式并没有考虑优先级约束。由于GAPS生成初始种群时不考虑优先级约束，所以它初始种群中有许多的解违背了任务的优先级约束，这些违背约束的解的适应值也增加了惩罚项，使得这些初始解的最优值远大于IGA的初始解的最优值。

为了进一步说明基于DAG的编码方式与加入先验知识的效果，本文在机器人数为5的情况下，即在小规模问题下测试有无先验知识的情况下的遗传算法的效果，并与GAPS与启发式算法进行比较。本文为不同的任务组规模生成10个问题实例用于测试，并计算测试结果的平均值作为结果。从表1中可以看到，当任务组数为1时，IGA相较于CHA、MIA和GAPS，目标函数分别减少了6.40%、4.61%和3.45%；当任务组数为2时，目标函数分别减少了13.84%、10.64%和25.71%；当任务组数为3时，目标函数分别减少了18.62%、13.06%和38.06%。这说明采用IGA得到的方案质量更高，随着任务组规模增加，质量的提升更显著。此外，在当任务组数为2和3时，IGAPK的目标函数相较于IGA分别减少了2.02%和1.64%。这表明加入先验知识初始化后，IGAPK的性能相较于IGA有了进一步的提升。

表1小规模问题上不同算法的目标函数值对比

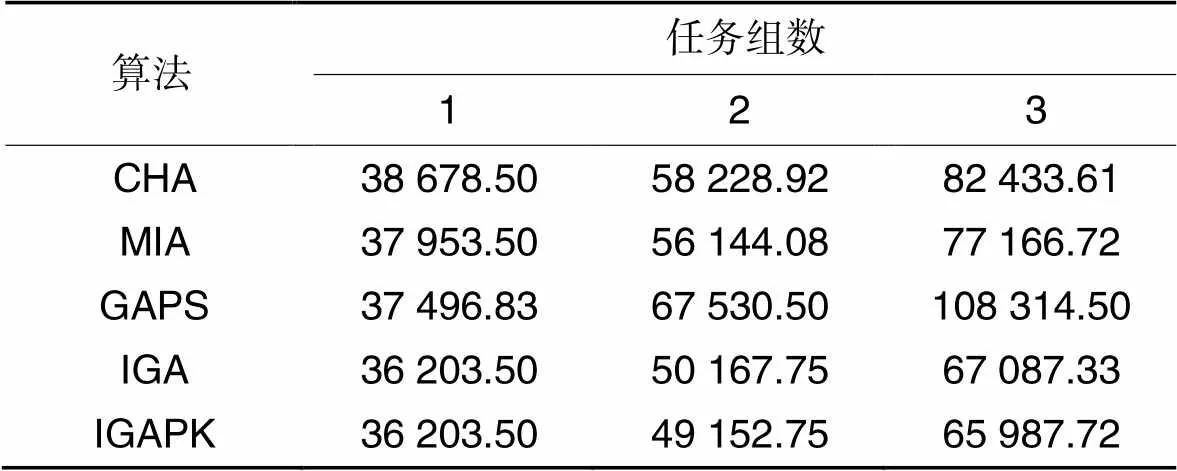
Tab.1　Comparison of objective function values of different algorithms on small-scale problems

3.2.2基于任务组的滚动调度策略对算法的提升

为了验证滚动调度策略在大规模问题下的效果，在机器人数为20的情况下，在不同任务组数下比较遗传算法使用与不使用滚动调度策略的效果，并与其他算法进行比较。每个任务需要的机器人数从［4，11］随机选取。本文为不同的任务组规模生成10个问题实例用于测试，并计算测试结果的平均值作为结果，在ACGARS中，任务组窗口的宽度设置为2个任务组，结果如表2所示。从表2中可见，当任务组数为10时，ACGARS相较于CHA、MIA、GAPS和IGAPK，目标函数分别减少了26.75%、17.42%、64.89%和14.96%；当任务组数为15时，目标函数分别减少了27.82%、17.22%、69.35%和17.04%；当任务组数为20时，目标函数分别减少了30.02%、16.86%、75.65%和16.34%。可以观察到，在大规模的问题下，GAPS的性能相较于其他算法显著下降，这是因为GAPS生成个体时不考虑任务优先级约束，在问题规模增大的情况下，任务的优先级约束更复杂，此时生成的个体更容易违背任务优先级约束，即使对违背约束的个体的适应度函数施加惩罚函数也难以搜寻到高质量的可行解，最终使它搜索效果变差。此外，从表2中还可以看到，IGAPK的性能相较于启发式算法虽然仍有一定的优势，但相较于在较小规模下的实验结果，生成方案的质量相较于启发式算法的优势程度有较明显的下降。原因是即使IGAPK的搜索效率相较于GAPS有提高，但所要搜索的解的数量随着问题规模呈指数增长，IGAPK仍难以在短时间内为大规模的问题生成高质量的解。使用基于任务组的滚动调度策略的ACGARS的性能相较于IGAPK有了提升，这是因为滚动调度策略虽然牺牲了整体的最优性导致理论上难以找到全局最优解，但减少了所需要搜索的解的数量，算法能在短时间内找到高质量的解。这也验证了在大规模问题下使用滚动调度策略的必要性。

表2大规模问题上不同算法的目标函数值对比

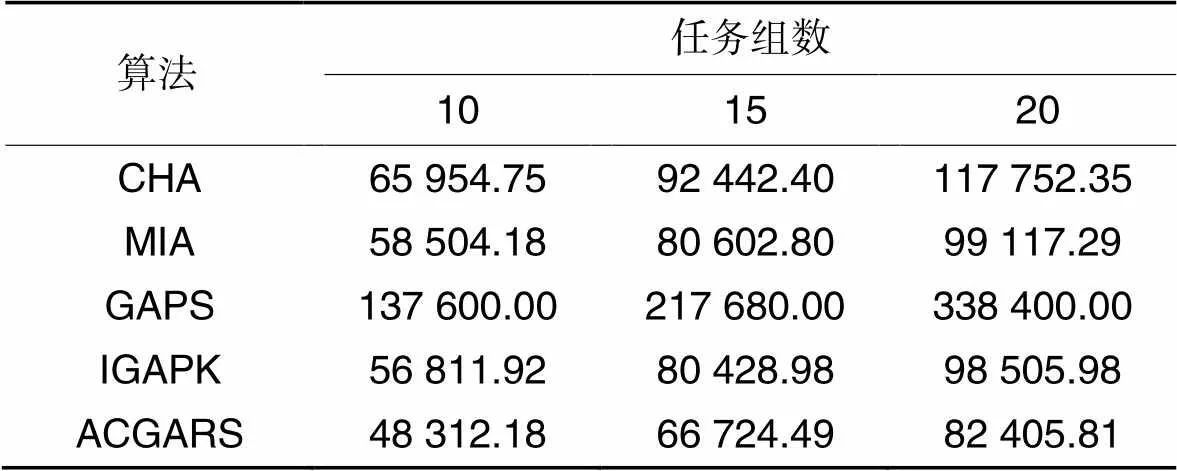
Tab.2　Comparison of objective function values of different algorithms on large-scale problems

最后，为了验证滚动调度策略对算法处理动态能力的影响，本文比较了IGAPK与ACGARS在求解相同规模问题时所需要的CPU时间，并与其他算法进行比较。如表3所示，可以发现，在使用滚动调度策略后，ACGARS在求解3个规模的问题所需的CPU时间相较于IGAPK分别缩短了76.05%、85.94%和91.81%。上述结果采用滚动调度策略能够缩短算法所需的CPU计算时间，从而能够在短时间内作出决策，增强了算法处理动态问题的能力。虽然计算时间相较于CHA、MIA这两个启发式算法长，但ACGARS的求解质量相较于CHA、MIA有明显提升，所以是可以接受的。

表3大规模问题上不同算法的CPU耗时对比 单位：s

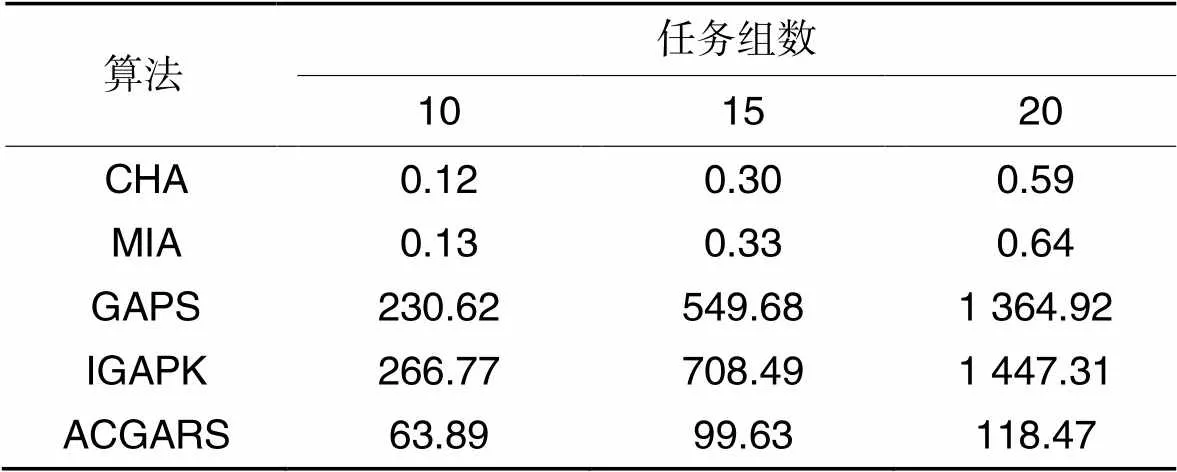
Tab.3　Comparison of CPU time consumption of different algorithms on large-scale problems unit：s

3.3　计算复杂性分析

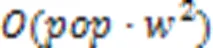
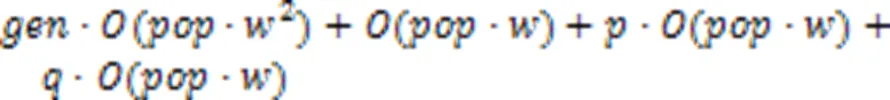
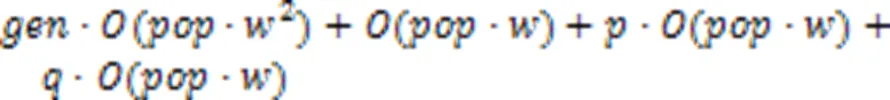
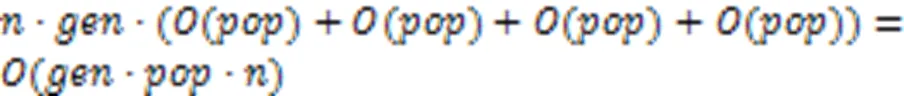
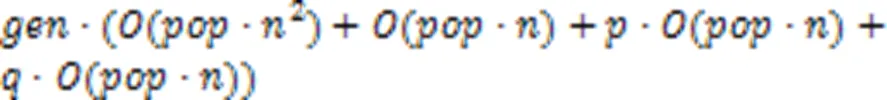
4 结语

针对已有遗传算法面对智能工厂中大规模多约束MRTA问题求解效果一般的问题，提出了结合遗传算法和滚动调度的MRTA算法（ACGARS）。首先采用基于DAG的编码方式，使得产生的解能满足任务优先级约束，提高算法的搜索效率；其次使用基于规则的启发式算法生成的方案作为先验知识加入初始种群，以进一步提高搜索效率；最后使用滚动调度策略，减小每次求解问题的规模。实验结果表明，本文算法优于现有的启发式与遗传算法，提高了多机器人团队的生产效率。下一步的研究工作考虑将更多的实际约束加入到问题中求解。

[1] LI X， LI D， WAN J， et al. A review of industrial wireless networks in the context of Industry 4.0 ［J］. Wireless Networks， 2017， 23（1）： 23-41.

[2] LIANG G， LUO H， LI M， et al. FreeBOT： a freeform modular self-reconfigurable robot with arbitrary connection point-design and implementation［C］// Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway： IEEE， 2020： 6506-6513.

[3] CHEN K-C， LIN S-C， HSIAO J-H， et al. Wireless networked multirobot systems in smart factories ［J］. Proceedings of the IEEE， 2020， 109（4）： 468-494.

[4] WANG S， WAN J， ZHANG D， et al. Towards smart factory for industry 4.0： a self-organized multi-agent system with big data based feedback and coordination ［J］. Computer Networks， 2016， 101： 158-168.

[5] FECZKO J， MANKA M， KROL P， et al. Review of the modular self reconfigurable robotic systems［C］// Proceedings of the 2015 10th International Workshop on Robot Motion and Control. Piscataway： IEEE， 2015： 182-187.

[6] 赵辉，郝梦雅，王红君，等. 基于资源拍卖的农业多机器人任务分配［J］.计算机应用与软件，2021，38（12）：286-290，313.（ZHAO H， HAO M Y， WANG H J， et al. Cooperative task allocation of agricultural multi-robot based on resource auction［J］. Computer Applications and Software， 2021，38（12）：286-290，313.）

[7] KIM J， SON H I. A Voronoi diagram-based workspace partition for weak cooperation of multi-robot system in orchard ［J］. IEEE Access， 2020， 8： 20676-20686.

[8] NIKITENKO A， LAVENDELIS E， EKMANIS M， et al. Task allocation methods for homogeneous multi-robot systems： feed pushing case study ［J］. Automatic Control and Computer Sciences， 2018， 52： 371-381.

[9] 林思梦. 基于粒子群算法的灾后救援多机器人任务分配［D］.徐州：中国矿业大学，2020： 2.（LIN S M. Multi-robot task allocation for rescue after disaster based on particle swarm optimization algorithm［D］. Xuzhou： China University of Mining and Technology， 2020： 2.）

[10] MOURADIAN C， SAHOO J， GLITHO R H， et al. A coalition formation algorithm for multi-robot task allocation in large-scale natural disasters ［C］// Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference. Piscataway： IEEE， 2017： 1909-1914.

[11] GUNN T， ANDERSON J. Dynamic heterogeneous team formation for robotic urban search and rescue ［J］. Journal of Computer and System Sciences， 2015， 81（3）： 553-567.

[12] 李鑫滨，章寿涛，闫磊，等. 基于鲁棒Restless Bandits模型的多水下自主航行器任务分配策略［J］.计算机应用，2019，39（10）：2795-2801.（LI X B， ZHANG S T， YAN L， et al. Multiple autonomous underwater vehicle task allocation policy based on robust Restless Bandit model［J］. Journal of Computer Applications， 2019，39（10）：2795-2801.）

[13] CARRENO Y， PAIRET È， PETILLOT Y， et al. A decentralized strategy for heterogeneous AUV missions via goal distribution and temporal planning ［C］// Proceedings of the 2020 International Conference on Automated Planning and Scheduling. Palo Alto： AAAI Press， 2020： 431-439.

[14] GUO X， HU J， CHEN J， et al. Semantic histogram based graph matching for real-time multi-robot global localization in large scale environment ［J］. IEEE Robotics and Automation Letters， 2021， 6（4）： 8349-8356.

[15] KORASH G A， STENTZ A， DIAS M B. A comprehensive taxonomy for multi-robot task allocation ［J］. The International Journal of Robotics Research， 2013， 32（12）：1495-1512.

[16] GERKEY B P， MATARIĆ M J. A formal analysis and taxonomy of task allocation in multi-robot systems ［J］. The International Journal of Robotics Research， 2004， 23（9）： 939-954.

[17] KORSAH G A， KANNAN B， BROWNING B， et al. xBots： an approach to generating and executing optimal multi-robot plans with cross-schedule dependencies［C］// Proceedings of the 2012 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2012： 115-122.

[18] WANG Z， GOMBOLAY M. Learning scheduling policies for multi-robot coordination with graph attention networks ［J］. IEEE Robotics and Automation Letters， 2020， 5（3）： 4509-4516.

[19] BISCHOFF E， MEYER F， INGA J， et al. Multi-robot task allocation and scheduling considering cooperative tasks and precedence constraints［C］// Proceedings of the 2020 IEEE International Conference on Systems， Man， and Cybernetics. Piscataway： IEEE， 2020： 3949-3956.

[20] BISCHOFF E， TEUFEL J， INGA J， et al. Towards interactive coordination of heterogeneous robotic teams — introduction of a reoptimization framework ［C］// Proceedings of the 2021 IEEE International Conference on Systems， Man， and Cybernetics. Piscataway： IEEE， 2021： 1380-1386.

[21] MILORADOVIĆ B， ÇÜRÜKLÜ B， EKSTRÖM M， et al. A genetic algorithm approach to multi-agent mission planning problems［C］// Proceedings of the 2020 9th International Conference on Operations Operations Research and Enterprise Systems. Cham： Springer， 2020： 109-134.

[22] MILORADOVIĆ B， ÇÜRÜKLÜ B， EKSTRÖM M， et al. Extended colored traveling salesperson for modeling multi-agent mission planning problems ［C］// Proceedings of the 2019 8th International Conference on Operations Research and Enterprise Systems. Cham： Springer， 2019： 237-244.

[23] QI B， PU L， XU C， et al. Multi-robot task assignment method in the construction waste sorting system ［C］// Proceedings of the 2022 IEEE International Conference on Mechatronics and Automation. Piscataway： IEEE， 2022： 1364-1369.

[24] CECHINEL A K， DE PIERI E R， FERNANDES PEREZ A L， et al. Multi-robot task allocation using island model genetic algorithm ［J］. IFAC-PapersonLine， 2021， 54（1）： 558-563.

[25] 范学满，薛昌友，张会.基于多种群遗传算法的多UUV任务分配方法［J］.水下无人系统学报，2022，30（5）：621-630.（FAN X M， XUE C Y， ZHANG H. Task assignment method for multiple UUVs based on multi-population genetic algorithm ［J］. Journal of Unmanned Undersea Systems，2022，30（5）：621-630.）

[26] RAMCHURN S D， POLUKAROV M， FARINELLI A， et al. Coalition formation with spatial and temporal constraints［C］// Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems. New York： ACM， 2010，3： 1181-1188.

[27] KOES M， NOURBAKHSH I， SYCARA K， et al. Heterogeneous multi-robot coordination with spatial and temporal constraints［C］// Proceedings of the 20th National Conference on Artificial Intelligence. Palo Alto： AAAI Press， 2005： 1292-1297.

[28] ZHANG Y， PARKER L E. Multi-robot task scheduling［C］// Proceedings of the 2013 IEEE International Conference on Robotics and Automation. Piscataway： IEEE， 2013： 2992-2998.

[29] 方剑，席裕庚.周期性和事件驱动的Job Shop滚动调度策略［J］.控制与决策，1997， 12（2）：159-162，166.（FANG J， XI Y G. A periodic and event-driven rolling horizon job shop scheduling strategy［J］. Control and Decision， 1997， 12（2）：159-162，166.）

[30] SUSLOVA E， FAZLI P. Multi-robot task allocation with time window and ordering constraints［C］// Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway： IEEE， 2020： 6909-6916.

[31] ENTEZARI Z， MAHOOTCHI M. Developing a mathematical model for staff routing and scheduling in home health care industries： genetic algorithm-based solution scheme ［J］. Scientia Iranica， 2021， 28（6）： 3692-3718.

Multi-robot task allocation algorithm combining genetic algorithm and rolling scheduling

DENG Fuqin1，2， HUANG Huanzhao1， TAN Chaoen1， FU Lanhui1， ZHANG Jianmin1， LAM Tinlun2*

（1，，529020，；2，，，518116，）

The purpose of research on Multi-Robot Task Allocation （MRTA） is to improve the task completion efficiency of robots in smart factories. Aiming at the deficiency of the existing algorithms in dealing with large-scale multi-constrained MRTA， an MRTA Algorithm Combining Genetic Algorithm and Rolling Scheduling （ACGARS） was proposed. Firstly， the coding method based on Directed Acyclic Graph （DAG） was adopted in genetic algorithm to efficiently deal with the priority constraints among tasks. Then， the prior knowledge was added to the initial population of genetic algorithm to improve the search efficiency of the algorithm. Finally， a rolling scheduling strategy based on task groups was designed to reduce the scale of the problem to be solved， thereby solving large-scale problems efficiently. Experimental results on large-scale problem instances show that compared with the schemes generated by Constructive Heuristic Algorithm （CHA）， MinInterfere Algorithm （MIA）， and Genetic Algorithm with Penalty Strategy （GAPS）， the scheme generated by the proposed algorithm has the average order completion time shortened by 30.02%， 16.86% and 75.65% respectively when the number of task groups is 20， which verifies that the proposed algorithm can effectively shorten the average waiting time of orders and improve the efficiency of multi-robot task allocation.

multi-robot task allocation; genetic algorithm; smart factory; Directed Acyclic Graph (DAG); rolling scheduling strategy

This work is partially supported by National Key Research and Development Program “Intelligent Robot” Key Project （2020YFB1313300）， Shenzhen Science and Technology Program （KQTD2016113010470345）， Exploratory Research Project of Shenzhen Institute of Artificial Intelligence and Robotics for Society （AC01202101103）， Wuyi University Horizontal Research Project （33520098）.

DENG Fuqin， born in 1982， Ph. D.， senior engineer. His research interests include machine learning， mobile robotic systems and multi-robot systems.

HUANG Huanzhao， born in 1998， M. S. candidate. His research interests include multi-robot task allocation.

TAN Chaoen， born in 1999， M. S. candidate. His research interests include multi-robot path planning.

FU Lanhui， born in 1987， Ph. D.， lecturer. His research interests include machine learning， image information processing.

ZHANG Jianmin， born in 1981， M. S.， lecturer. His research interests include machine learning， mobile robotic systems and multi-robot systems.

LAM Tinlun， born in 1984， Ph. D.， assistant professor. His research interests include modular self-reconfigurable robots， multi-robot systems.

TP242

A

1001-9081（2023）12-3833-07

10.11772/j.issn.1001-9081.2022121916

2023⁃01⁃04；

2023⁃02⁃21；

2023⁃02⁃22。

国家重点研发计划“智能机器人”重点专项（2020YFB1313300）；深圳市科技计划项目（KQTD2016113010470345）；深圳市人工智能与机器人研究院探索性研究项目（AC01202101103）；五邑大学横向课题项目（33520098）。

邓辅秦（1982—），男，湖南郴州人，高级工程师，博士，主要研究方向：机器学习、移动机器人系统与多机器人系统；黄焕钊（1998—），男，广东汕头人，硕士研究生，主要研究方向：多机器人任务分配；谭朝恩（1999—），男，广东顺德人，硕士研究生，主要研究方向：多机器人路径规划；付兰慧（1987—），女，河南新乡人，讲师，博士，主要研究方向：机器学习、图像信息处理；张建民（1981—），男，河北沧州人，讲师，硕士，主要研究方向：机器学习、移动机器人系统与多机器人系统；林天麟（1984—），男，香港人，助理教授，博士，CCF会员，主要研究方向：模块化自重构机器人、多机器人系统。